28.2解直角三角形(第2课时)
文档属性
| 名称 | 28.2解直角三角形(第2课时) |  | |
| 格式 | rar | ||
| 文件大小 | 596.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-22 13:18:00 | ||
图片预览



文档简介
课件19张PPT。解直角三角形的应用(一)通州育才中学 吴锋 2008-11-28解直角
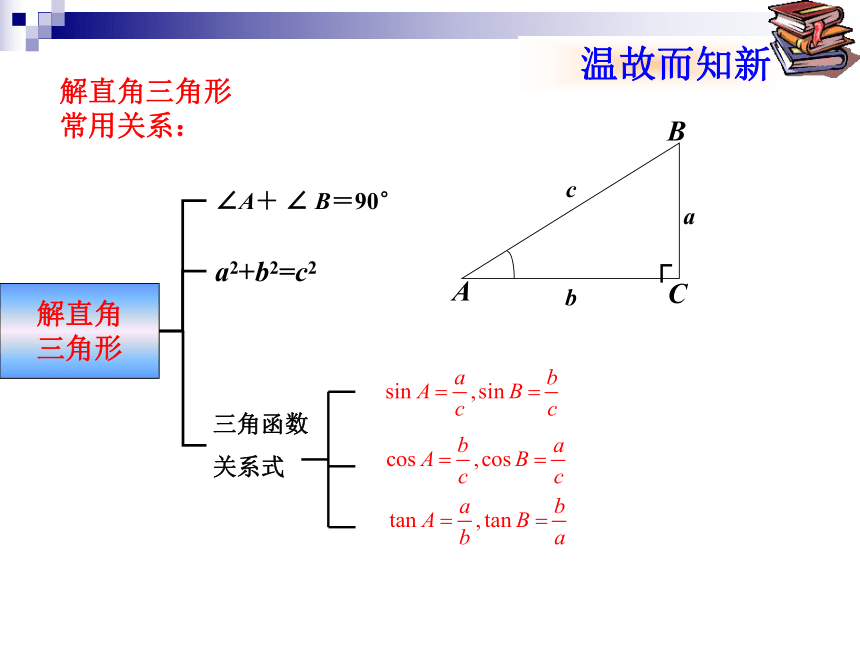
三角形∠A+ ∠ B=90°a2+b2=c2三角函数
关系式解直角三角形常用关系:如图,Rt△ABC中,∠C=90°,(1)若∠A=30°,BC=3,则AC=(2)若∠B=60°,AC=3,则BC=(3)若∠A=α°,AC=3,则BC=(4)若∠A=α°,BC=m,则AC=【例1】如图,直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为α=30°,β=45°,求大桥的长AB .450米解:由题意得,在Rt△PAO与Rt△PBO中
PAB
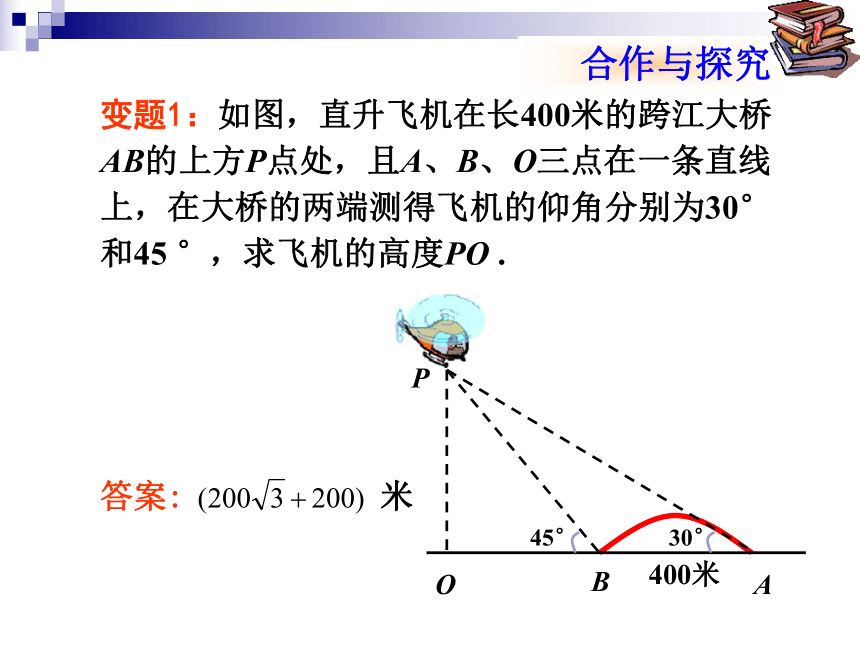
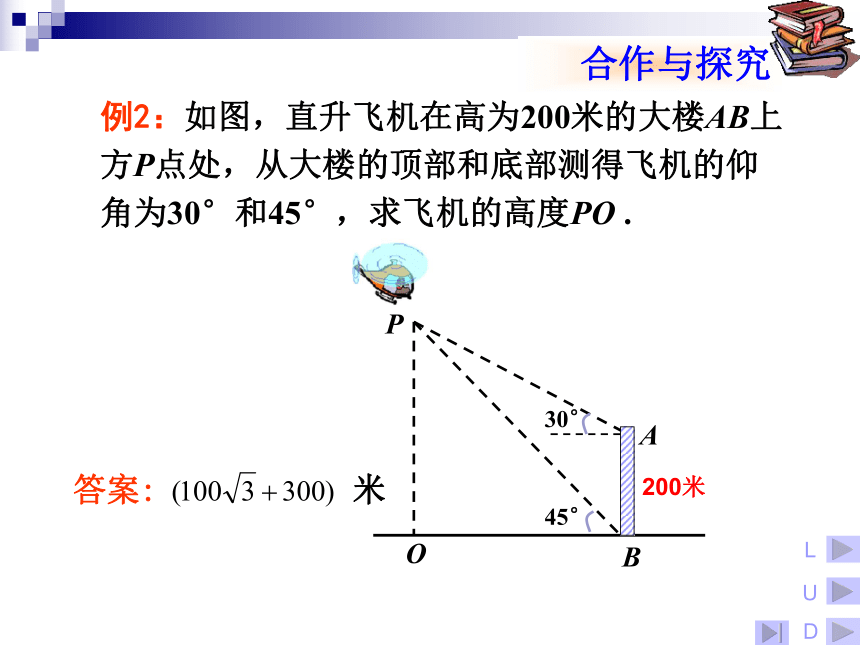
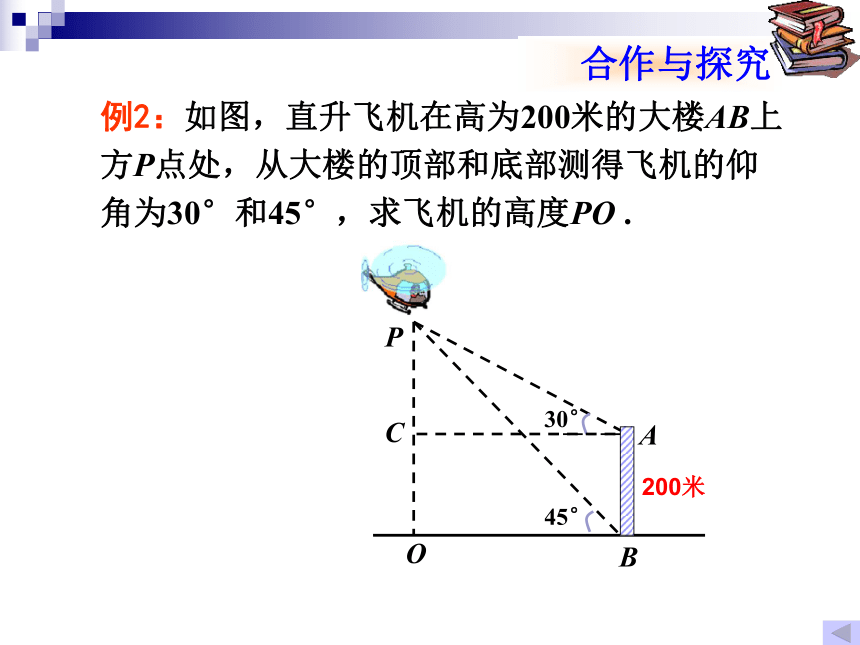
变题1:如图,直升飞机在长400米的跨江大桥AB的上方P点处,且A、B、O三点在一条直线上,在大桥的两端测得飞机的仰角分别为30°和45 °,求飞机的高度PO .AB400米PBA200米例2:如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .LUDP例2:如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .PBA200米CPBA200米C例2:如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .例2:如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .PBA200米C200米POBA变题2:如图,直升飞机在高为200米的大楼AB左侧P点处,测得大楼的顶部仰角为45°,测得大楼底部俯角为30°,求飞机与大楼之间的水平距离.45°30°45060°45°20020045°30°30°45°450小刘想测量学校操场旗杆顶端到地面的距离,但旗杆底部不能直接到达,请你应用今天所学知识,帮助他设计一个测量方案,画出示意图,相关数据用字母表示,并与同学交流。1.数形结合思想.方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.解题思想与方法小结:2.方程思想.3.转化(化归)思想.2.如图2,在离铁塔BE 120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE= _________ (根号保留).1.如图1,已知楼房AB高为50m,铁塔塔基距楼房地基间的水平距离BD为100m,塔高CD为 m,则下面结论中正确的是( )
A.由楼顶望塔顶仰角为60°
B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30°
D.由楼顶望塔基俯角为30°C3.如图3,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200m,点C在BD上,则树高AB等于 (根号保留).4.如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°
,则折叠后重叠部分的面积为 (根号保留). 思考:有一块三形场地ABC,测得其中AB边长为60米,AC边长50米,∠ABC=30°,试求出这个三角形场地的面积.作业必做题:
书本P96/4、P97/7题.
选做题:
1.一架直升机从某塔顶A测得地面C、D两点的俯角分别为30°、 45°,若C、D与塔底B共线,CD=200米,求塔高AB?
2.有一块三形场地ABC,测得其中AB边长为60米,AC边长50米,∠ABC=30°,试求出这个三角形场地的面积.3.学生小王帮在测绘局工作的爸爸买了一些仪器后与同学在环西文化广场休息,看到濠河对岸的电视塔,他想用手中的测角仪和卷尺不过河测出电视塔空中塔楼的高度.现已测出∠ADB=40°,由于不能过河,因此无法知道BD的长度,于是他向前走50米到达C处测得∠ACB=55°,但他们在计算中碰到了困难,请大家一起想想办法,求出电视塔塔楼AB的高.答案:空中塔楼AB高约为105米视线视线仰角俯角在进行观察或测量时,从上往下看,视线与水平线的夹角叫做俯角.从下向上看,视线与水平线的夹角叫做仰角;
三角形∠A+ ∠ B=90°a2+b2=c2三角函数
关系式解直角三角形常用关系:如图,Rt△ABC中,∠C=90°,(1)若∠A=30°,BC=3,则AC=(2)若∠B=60°,AC=3,则BC=(3)若∠A=α°,AC=3,则BC=(4)若∠A=α°,BC=m,则AC=【例1】如图,直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为α=30°,β=45°,求大桥的长AB .450米解:由题意得,在Rt△PAO与Rt△PBO中
PAB
变题1:如图,直升飞机在长400米的跨江大桥AB的上方P点处,且A、B、O三点在一条直线上,在大桥的两端测得飞机的仰角分别为30°和45 °,求飞机的高度PO .AB400米PBA200米例2:如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .LUDP例2:如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .PBA200米CPBA200米C例2:如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .例2:如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .PBA200米C200米POBA变题2:如图,直升飞机在高为200米的大楼AB左侧P点处,测得大楼的顶部仰角为45°,测得大楼底部俯角为30°,求飞机与大楼之间的水平距离.45°30°45060°45°20020045°30°30°45°450小刘想测量学校操场旗杆顶端到地面的距离,但旗杆底部不能直接到达,请你应用今天所学知识,帮助他设计一个测量方案,画出示意图,相关数据用字母表示,并与同学交流。1.数形结合思想.方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.解题思想与方法小结:2.方程思想.3.转化(化归)思想.2.如图2,在离铁塔BE 120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE= _________ (根号保留).1.如图1,已知楼房AB高为50m,铁塔塔基距楼房地基间的水平距离BD为100m,塔高CD为 m,则下面结论中正确的是( )
A.由楼顶望塔顶仰角为60°
B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30°
D.由楼顶望塔基俯角为30°C3.如图3,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200m,点C在BD上,则树高AB等于 (根号保留).4.如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°
,则折叠后重叠部分的面积为 (根号保留). 思考:有一块三形场地ABC,测得其中AB边长为60米,AC边长50米,∠ABC=30°,试求出这个三角形场地的面积.作业必做题:
书本P96/4、P97/7题.
选做题:
1.一架直升机从某塔顶A测得地面C、D两点的俯角分别为30°、 45°,若C、D与塔底B共线,CD=200米,求塔高AB?
2.有一块三形场地ABC,测得其中AB边长为60米,AC边长50米,∠ABC=30°,试求出这个三角形场地的面积.3.学生小王帮在测绘局工作的爸爸买了一些仪器后与同学在环西文化广场休息,看到濠河对岸的电视塔,他想用手中的测角仪和卷尺不过河测出电视塔空中塔楼的高度.现已测出∠ADB=40°,由于不能过河,因此无法知道BD的长度,于是他向前走50米到达C处测得∠ACB=55°,但他们在计算中碰到了困难,请大家一起想想办法,求出电视塔塔楼AB的高.答案:空中塔楼AB高约为105米视线视线仰角俯角在进行观察或测量时,从上往下看,视线与水平线的夹角叫做俯角.从下向上看,视线与水平线的夹角叫做仰角;
