勾股定理(新疆维吾尔自治区乌鲁木齐市新市区)
文档属性
| 名称 | 勾股定理(新疆维吾尔自治区乌鲁木齐市新市区) |

|
|
| 格式 | rar | ||
| 文件大小 | 500.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-21 00:00:00 | ||
图片预览







文档简介
课件31张PPT。七十六中欢迎您!授课人:陈梅
乌市第76中学
人教版《数学》
八年级(下)
第18章“18.1勾股定理”
解直角三角形一、教材分析 勾股定理是千古第一定理,在数学发展中起过重要的作用,是反映自然界基本规律的一条重要结论。勾股定理是学生在已经掌握了直角三角形有关性质的基础上进行学习的,它是直角三角形的一条非常重要的性质,揭示的是直角三角形中三边的数量关系,它为以后学习解直角三角形奠定了基础,在实际生活中用途很大。认知分析:学生已经掌握了直角三角形有关性质。
能力分析:初二学生已具备一定的分析、归纳的能力和运用数学的思想意识。对于勾股定理的得出,需要学生通过动手操作,在观察的基础上,大胆猜想数学结论,但学生在这一方面的可预见性和耐挫折能力并不是很成熟,从而形成困难。
情感与学习风格分析:学生比较活跃,两极分化较严重,他们喜欢学习生动活泼的内容,并乐于用自己的方式去学习,所以由学生本人把要学的东西自己去发现或创造出来,对学生较适宜,且有一定吸引力,可进一步调动学生强烈求知欲。 二、学生情况分析三、教学目标 1、知识与技能
让学生通过观察、计算、猜想直角三角形两条直角边的平方和等于斜边的平方的结论。
2、数学思考
通过观察、交流、归纳等过程,培养学生探究问题的能力、观察能力、以及与他人合作交流的能力.
3、解决问题
在学生充分观察、归纳、猜想、探索直角三角形两条直角边的平方和等于斜边的平方的过程中,发展合情推理能力,体会数形结合的思想。
4、情感与态度
培养学生积极参与、合作交流的意识。在探索勾股定理的过程中,体验获得结论的快乐,锻炼克服困难的勇气。四、教学重点与难点 1、教学重点:探索直角三角形两条直角边的平方和与斜边的平方的结论,从而发现勾股定理。
2、教学难点:以直角三角形的边为边的正方形面积的计算。 五、教法与学法 数学是一门培养人的思维,发展人的思维的重要学科,因此在教学中,不仅要使学生“知其然”,而且还要使学生“知其所以然”。针对八年级学生的认知结构和心理特征,本节课选择“引导探索法”,由浅到深,由特殊到一般的提出问题,把教学过程化为亲身观察,自主探究,合作交流,归纳总结的过程。再现知识的发生,发展和形成的过程。充分体现教师是教学活动的组织者,引导者,合作者,学生是学习的主体。六、教具准备1、多媒体课件 2、直尺
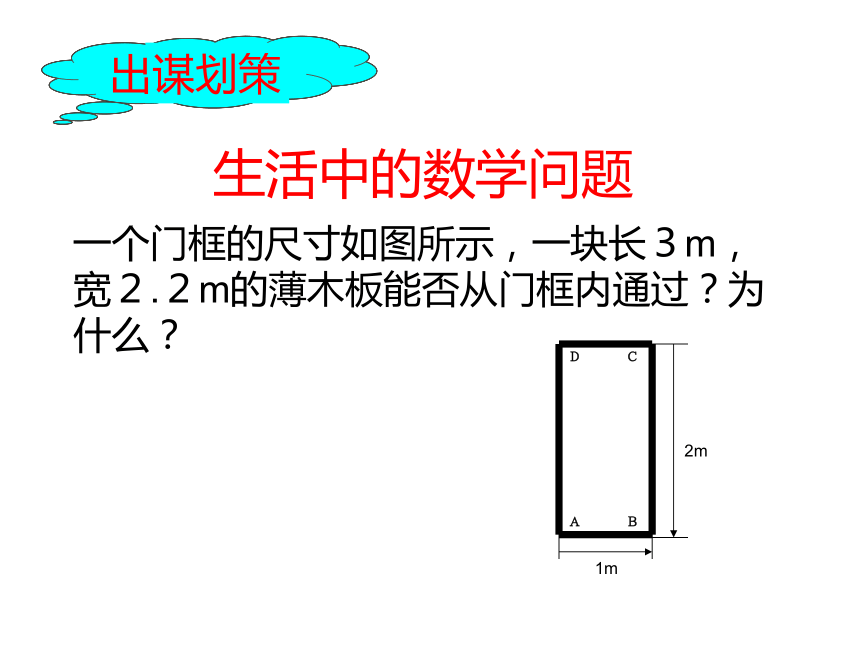
3、网格纸七、教学过程问题情境分析探究得出猜想实践验证生活中的数学问题一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?D C
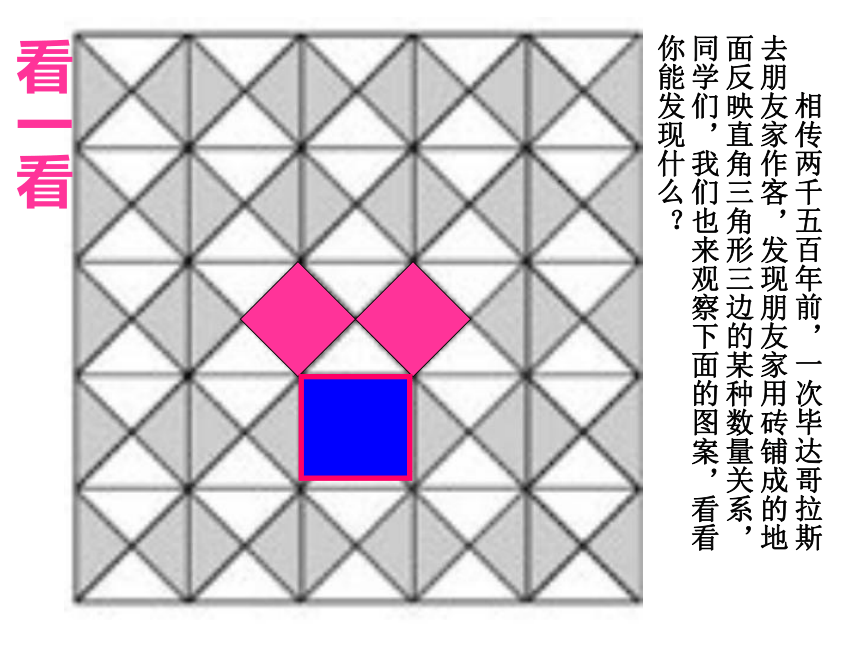
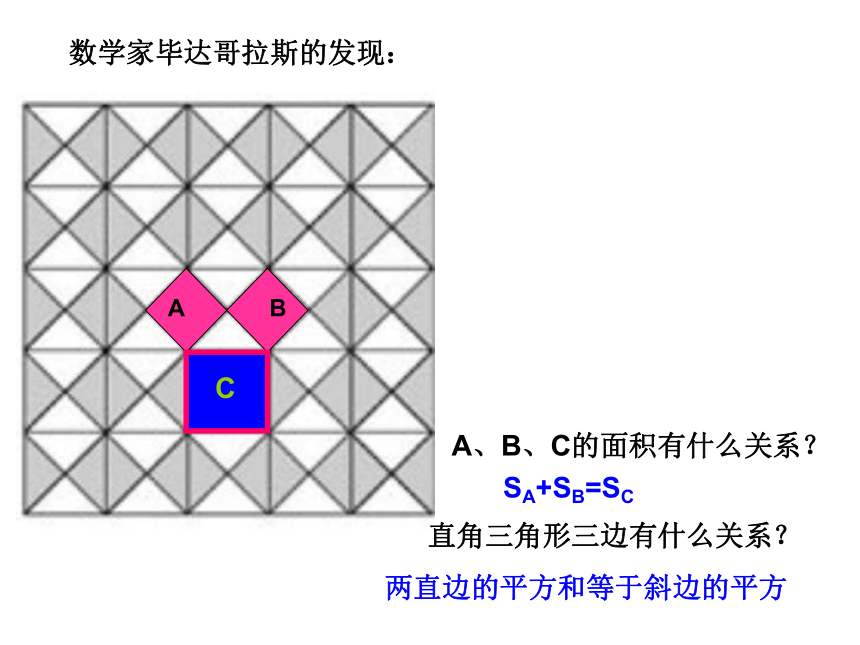
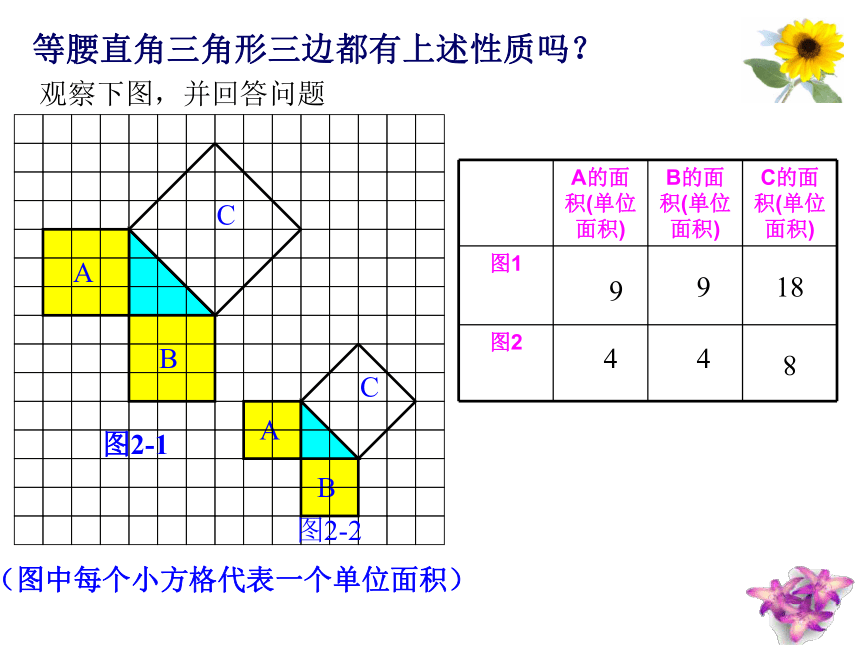
A B2m1m出谋划策看一看 相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么? 数学家毕达哥拉斯的发现:A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方等腰直角三角形三边都有上述性质吗?9918448观察下图,并回答问题 SA+SB=SC448两直角边的平方和
等于斜边的平方分“割”成4个直角边为整数的三角形(单位面积)(单位面积)把C看 成边长为6的正方形面积,减去4个直角边为分别3的等腰直角三角形的面积探究二:一般的直角三角形三边之间是否也有这一性质?164925913思考:面积A,B,C还有上述关系吗?
探究二:一般的直角三角形三边之间是否也有这一性质? SA+SB=SC两直角边的平方和
等于斜边的平方分割成4个直角边为整数的三角形(面积单位)把C看成边长为7的正方形面积减去4个直角边分别为3、4的直角三角形的面积(面积单位)CacbSA+SB=SC设:直角三角形的三边长分别是a、b、c猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.勾股弦 勾股定理(毕达哥拉斯定理)例.求出下列直角三角形中未知边的长度5x13学以致用,做一做解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2X2 =36+64x2 =100x2=62+82∴ x=10 ∵x>0 x2+52=132 x2=132-52x2=144∴ x=12(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2∵x>0ACBACB做一做: P625400P的面积 =______________225BACAB=__________AC=__________BC=__________2515202.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做比一比看看谁算得快!3.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做生活中的数学问题一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?D C
A B2m1m出谋划策 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。3、学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。
作业:
1、三导练习册:18.1勾股定理(一)
2、思考、查阅勾股定理的证明方法。敬请指导再见八、评价分析1、注意评价内容的多元化
通过课堂中学生展示自己对所学内容的理解,交流对某一问题的看法,各种问题尝试解答等活动,使教师从学生思维活动、有关内容的理解和掌握,以及学生参与活动的程序等多层面地了解学生。
2、注重对学生学习过程的评价
在整个教学过程中,通过对学生参与数学活动的程度、自信心、合作交流的意识以及独立思考的习惯,发现问题的能力进行评价,并对学生中出现的独特的想法或结论给予鼓励性评价。
3、 德国教育家第多斯惠指出:“教学的艺术不在于传授本领,而在于激励、唤醒、鼓舞。”有效的导入就能激励、唤醒、鼓舞学生。上课伊始,学生的学习心理准备难免不充分,师生之间难免有一定的心理距离。这里通过联系实际问题和毕达哥拉斯的传说来激发学生学习的兴趣。并且让学生体会到数学来源于生活,引导学生用数学的眼光观察生活中的有关问题.
4、训练反馈是学习的一个重要环节,既能让学生获得成功的喜悦,提高学习能力,又能及时找出不足,调整学习目标,促进自身发展.
乌市第76中学
人教版《数学》
八年级(下)
第18章“18.1勾股定理”
解直角三角形一、教材分析 勾股定理是千古第一定理,在数学发展中起过重要的作用,是反映自然界基本规律的一条重要结论。勾股定理是学生在已经掌握了直角三角形有关性质的基础上进行学习的,它是直角三角形的一条非常重要的性质,揭示的是直角三角形中三边的数量关系,它为以后学习解直角三角形奠定了基础,在实际生活中用途很大。认知分析:学生已经掌握了直角三角形有关性质。
能力分析:初二学生已具备一定的分析、归纳的能力和运用数学的思想意识。对于勾股定理的得出,需要学生通过动手操作,在观察的基础上,大胆猜想数学结论,但学生在这一方面的可预见性和耐挫折能力并不是很成熟,从而形成困难。
情感与学习风格分析:学生比较活跃,两极分化较严重,他们喜欢学习生动活泼的内容,并乐于用自己的方式去学习,所以由学生本人把要学的东西自己去发现或创造出来,对学生较适宜,且有一定吸引力,可进一步调动学生强烈求知欲。 二、学生情况分析三、教学目标 1、知识与技能
让学生通过观察、计算、猜想直角三角形两条直角边的平方和等于斜边的平方的结论。
2、数学思考
通过观察、交流、归纳等过程,培养学生探究问题的能力、观察能力、以及与他人合作交流的能力.
3、解决问题
在学生充分观察、归纳、猜想、探索直角三角形两条直角边的平方和等于斜边的平方的过程中,发展合情推理能力,体会数形结合的思想。
4、情感与态度
培养学生积极参与、合作交流的意识。在探索勾股定理的过程中,体验获得结论的快乐,锻炼克服困难的勇气。四、教学重点与难点 1、教学重点:探索直角三角形两条直角边的平方和与斜边的平方的结论,从而发现勾股定理。
2、教学难点:以直角三角形的边为边的正方形面积的计算。 五、教法与学法 数学是一门培养人的思维,发展人的思维的重要学科,因此在教学中,不仅要使学生“知其然”,而且还要使学生“知其所以然”。针对八年级学生的认知结构和心理特征,本节课选择“引导探索法”,由浅到深,由特殊到一般的提出问题,把教学过程化为亲身观察,自主探究,合作交流,归纳总结的过程。再现知识的发生,发展和形成的过程。充分体现教师是教学活动的组织者,引导者,合作者,学生是学习的主体。六、教具准备1、多媒体课件 2、直尺
3、网格纸七、教学过程问题情境分析探究得出猜想实践验证生活中的数学问题一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?D C
A B2m1m出谋划策看一看 相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么? 数学家毕达哥拉斯的发现:A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方等腰直角三角形三边都有上述性质吗?9918448观察下图,并回答问题 SA+SB=SC448两直角边的平方和
等于斜边的平方分“割”成4个直角边为整数的三角形(单位面积)(单位面积)把C看 成边长为6的正方形面积,减去4个直角边为分别3的等腰直角三角形的面积探究二:一般的直角三角形三边之间是否也有这一性质?164925913思考:面积A,B,C还有上述关系吗?
探究二:一般的直角三角形三边之间是否也有这一性质? SA+SB=SC两直角边的平方和
等于斜边的平方分割成4个直角边为整数的三角形(面积单位)把C看成边长为7的正方形面积减去4个直角边分别为3、4的直角三角形的面积(面积单位)CacbSA+SB=SC设:直角三角形的三边长分别是a、b、c猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.勾股弦 勾股定理(毕达哥拉斯定理)例.求出下列直角三角形中未知边的长度5x13学以致用,做一做解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2X2 =36+64x2 =100x2=62+82∴ x=10 ∵x>0 x2+52=132 x2=132-52x2=144∴ x=12(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2∵x>0ACBACB做一做: P625400P的面积 =______________225BACAB=__________AC=__________BC=__________2515202.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做比一比看看谁算得快!3.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做生活中的数学问题一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?D C
A B2m1m出谋划策 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。3、学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。
作业:
1、三导练习册:18.1勾股定理(一)
2、思考、查阅勾股定理的证明方法。敬请指导再见八、评价分析1、注意评价内容的多元化
通过课堂中学生展示自己对所学内容的理解,交流对某一问题的看法,各种问题尝试解答等活动,使教师从学生思维活动、有关内容的理解和掌握,以及学生参与活动的程序等多层面地了解学生。
2、注重对学生学习过程的评价
在整个教学过程中,通过对学生参与数学活动的程度、自信心、合作交流的意识以及独立思考的习惯,发现问题的能力进行评价,并对学生中出现的独特的想法或结论给予鼓励性评价。
3、 德国教育家第多斯惠指出:“教学的艺术不在于传授本领,而在于激励、唤醒、鼓舞。”有效的导入就能激励、唤醒、鼓舞学生。上课伊始,学生的学习心理准备难免不充分,师生之间难免有一定的心理距离。这里通过联系实际问题和毕达哥拉斯的传说来激发学生学习的兴趣。并且让学生体会到数学来源于生活,引导学生用数学的眼光观察生活中的有关问题.
4、训练反馈是学习的一个重要环节,既能让学生获得成功的喜悦,提高学习能力,又能及时找出不足,调整学习目标,促进自身发展.
