4.4 探索三角形相似的条件 同步练习 2023—2024学年北师大版数学九年级上册(无答案)
文档属性
| 名称 | 4.4 探索三角形相似的条件 同步练习 2023—2024学年北师大版数学九年级上册(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 123.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 00:00:00 | ||
图片预览

文档简介
北师大版九年级上4.4 探索三角形相似的条件
一、选择题
1.如图,下列选项中不能判定的是( )
A . B .
C . D .
2.如图,在□ABCD中,点E在边AD上,射线CE、BA交于点F,下列等式成立的是( )
A . B . C . D .
3.如图,AD,BC相交于点O,由下列条件仍不能判定△AOB与△DOC相似的是( )
A . AB∥CD B . ∠C=∠B C . D .
4.已知点P是线段AB的黄金分割点,且,则下列比例式能成立的是( )
A . B . C . D .
5.已知点P是线段AB的一个黄金分割点(AP>PB),则PB:AB的值为( )
A . B . C . D .
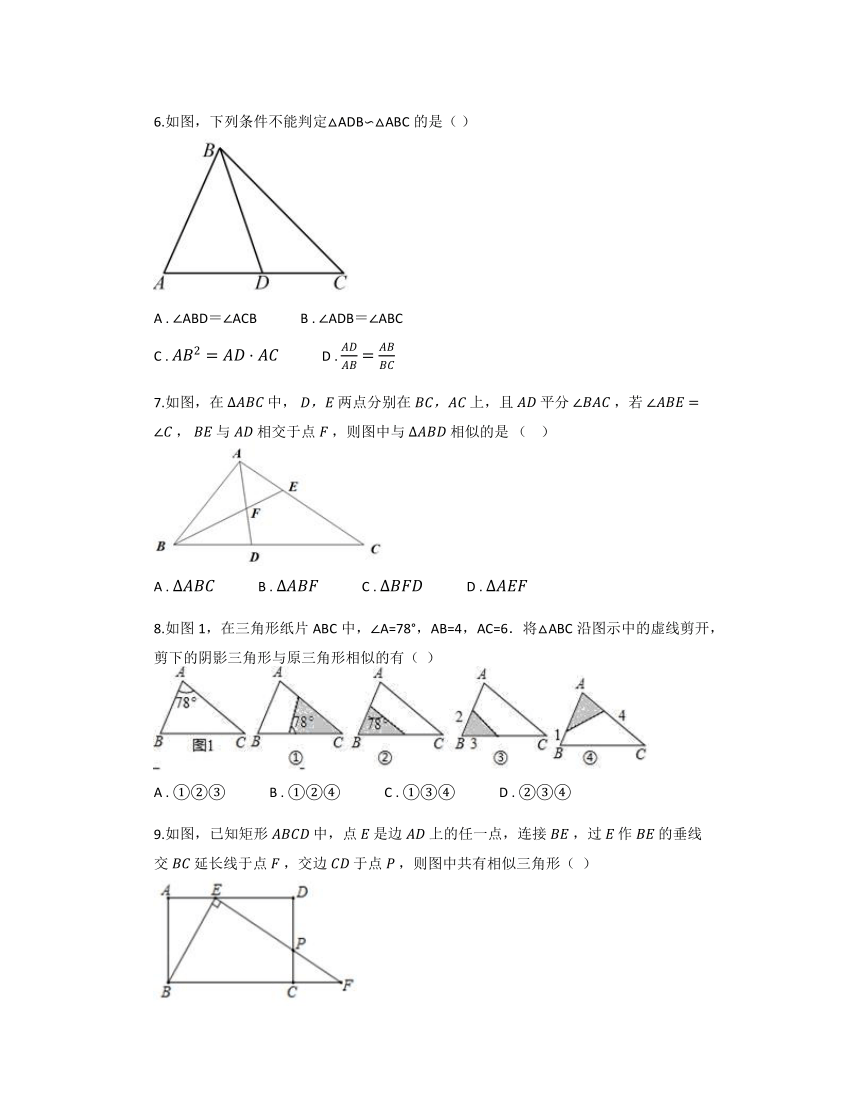
6.如图,下列条件不能判定△ADB∽△ABC的是( )
A . ∠ABD=∠ACB B . ∠ADB=∠ABC
C . D .
7.如图,在 中, 两点分别在 上,且 平分 ,若 , 与 相交于点 ,则图中与 相似的是 ( )
A . B . C . D .
8.如图1,在三角形纸片ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形相似的有( )
A . ①②③ B . ①②④ C . ①③④ D . ②③④
9.如图,已知矩形 中,点 是边 上的任一点,连接 ,过 作 的垂线交 延长线于点 ,交边 于点 ,则图中共有相似三角形( )
A . 6对 B . 5对 C . 4对 D . 3对
10.如图,在△ABC中,点P为AB上一点,给出下列四个条件:
①∠ACP=∠B; ②∠APC=∠ACB;③AC2=AP·AB;④AB·CP=AP·CB.其中能满足△APC和△ACB相似的条件是 ( )
A . ①②④ B . ①③④ C . ②③④ D . ①②③
11.如图,电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20m,试计算主持人应走到离A点大约( )m处是比较得体的位置.
A . 12.36m B . 7.64m C . 12.36m或7.64m D . 13.36m
12.下列命题中正确的是( )
①三边对应成比例的两个三角形相似
②二边对应成比例且一个角对应相等的两个三角形相似
③一个锐角对应相等的两个直角三角形相似
④一个角对应相等的两个等腰三角形相似.
A . ①③ B . ①④ C . ①②④ D . ①③④
二、填空题
13.已知线段,C是AB的黄金分割点,且,则_____.(结果保留根号)
14.已知点C是线段AB的黄金分割点( ),AB=4,则AC=_____.
15. 的边长分别为 的边长分别 ,则 与 _____(选填“一定”“不一定” “一定不”)相似
16.学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如上图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”,那么你认为△A1B1C1和△A2B2C2_____,(相似或不相似);理由是_____.
三、解答题
17.如图,已知AD·AC=AB·AE,∠DAE=∠BAC。求证:△DAB∽△EAC .
18.如图所示,点D在△ABC的AB边上,AD=2,BD=4,AC=2 .求证:△ACD∽△ABC.
19.已知:如图,点C,D在线段AB上,△PCD是等边三角形,且AC=1,CD=2,DB=4.
求证:△ACP∽△PDB.
20.如图,将非等腰△ABC绕点B旋转得到△DBE,且A,D,C三点在同一条直线上,BC、DE交与点O,连结EC.补全图形后,在现有图形下找出一对相似比不是1:1的相似三角形并进行证明.
一、选择题
1.如图,下列选项中不能判定的是( )
A . B .
C . D .
2.如图,在□ABCD中,点E在边AD上,射线CE、BA交于点F,下列等式成立的是( )
A . B . C . D .
3.如图,AD,BC相交于点O,由下列条件仍不能判定△AOB与△DOC相似的是( )
A . AB∥CD B . ∠C=∠B C . D .
4.已知点P是线段AB的黄金分割点,且,则下列比例式能成立的是( )
A . B . C . D .
5.已知点P是线段AB的一个黄金分割点(AP>PB),则PB:AB的值为( )
A . B . C . D .
6.如图,下列条件不能判定△ADB∽△ABC的是( )
A . ∠ABD=∠ACB B . ∠ADB=∠ABC
C . D .
7.如图,在 中, 两点分别在 上,且 平分 ,若 , 与 相交于点 ,则图中与 相似的是 ( )
A . B . C . D .
8.如图1,在三角形纸片ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形相似的有( )
A . ①②③ B . ①②④ C . ①③④ D . ②③④
9.如图,已知矩形 中,点 是边 上的任一点,连接 ,过 作 的垂线交 延长线于点 ,交边 于点 ,则图中共有相似三角形( )
A . 6对 B . 5对 C . 4对 D . 3对
10.如图,在△ABC中,点P为AB上一点,给出下列四个条件:
①∠ACP=∠B; ②∠APC=∠ACB;③AC2=AP·AB;④AB·CP=AP·CB.其中能满足△APC和△ACB相似的条件是 ( )
A . ①②④ B . ①③④ C . ②③④ D . ①②③
11.如图,电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20m,试计算主持人应走到离A点大约( )m处是比较得体的位置.
A . 12.36m B . 7.64m C . 12.36m或7.64m D . 13.36m
12.下列命题中正确的是( )
①三边对应成比例的两个三角形相似
②二边对应成比例且一个角对应相等的两个三角形相似
③一个锐角对应相等的两个直角三角形相似
④一个角对应相等的两个等腰三角形相似.
A . ①③ B . ①④ C . ①②④ D . ①③④
二、填空题
13.已知线段,C是AB的黄金分割点,且,则_____.(结果保留根号)
14.已知点C是线段AB的黄金分割点( ),AB=4,则AC=_____.
15. 的边长分别为 的边长分别 ,则 与 _____(选填“一定”“不一定” “一定不”)相似
16.学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如上图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”,那么你认为△A1B1C1和△A2B2C2_____,(相似或不相似);理由是_____.
三、解答题
17.如图,已知AD·AC=AB·AE,∠DAE=∠BAC。求证:△DAB∽△EAC .
18.如图所示,点D在△ABC的AB边上,AD=2,BD=4,AC=2 .求证:△ACD∽△ABC.
19.已知:如图,点C,D在线段AB上,△PCD是等边三角形,且AC=1,CD=2,DB=4.
求证:△ACP∽△PDB.
20.如图,将非等腰△ABC绕点B旋转得到△DBE,且A,D,C三点在同一条直线上,BC、DE交与点O,连结EC.补全图形后,在现有图形下找出一对相似比不是1:1的相似三角形并进行证明.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
