7.3平行线的判定 同步练习 (无答案) 2023—2024学年北师大版数学八年级上册
文档属性
| 名称 | 7.3平行线的判定 同步练习 (无答案) 2023—2024学年北师大版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 110.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 11:24:48 | ||
图片预览

文档简介
北师大版八年级上7.3平行线的判定
一、选择题
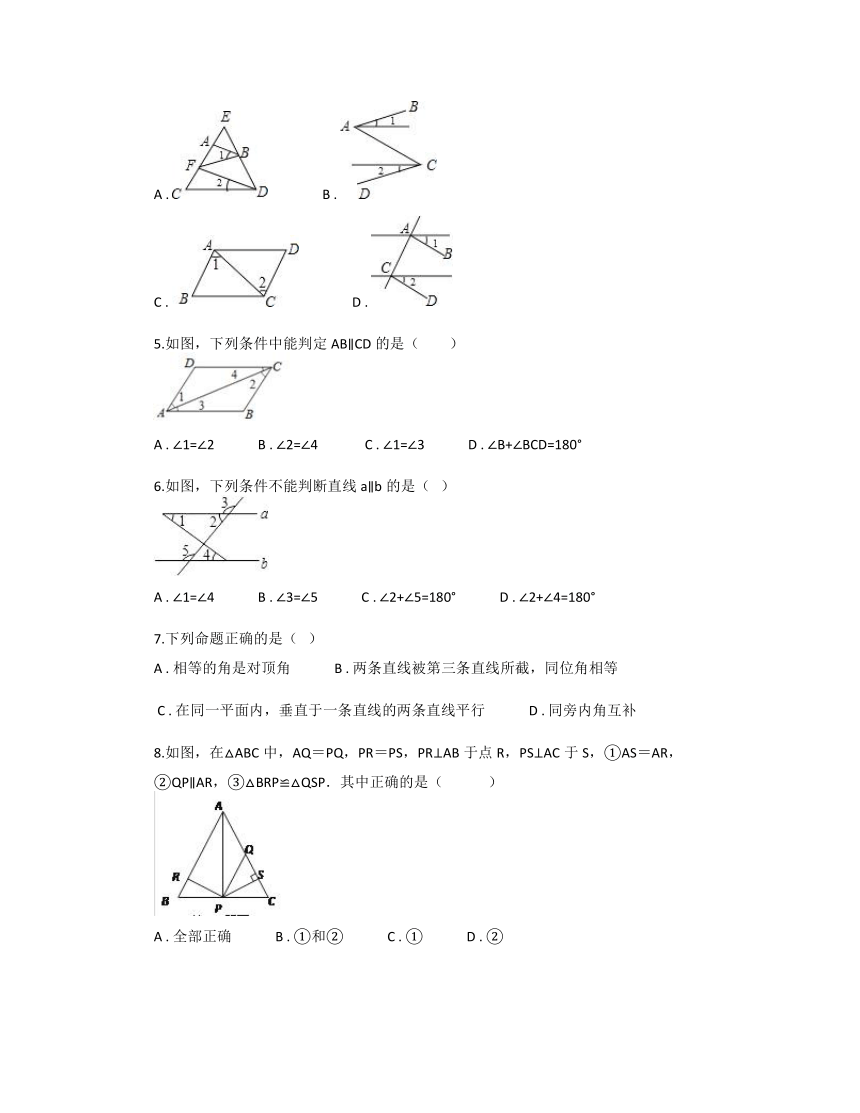
1.下列四个图形中∠1=∠2,能够判定AB∥CD的是( )
A . B .
C . D .
2.如图,如果,那么,其依据可以简单说成( )
A . 两直线平行,内错角相等 B . 内错角相等,两直线平行
C . 两直线平行,同位角相等 D . 同位角相等,两直线平行
3.如图,下列推理中正确的是( )
A . ∵∠1=∠4, ∴BC//AD B . ∵∠2=∠3,∴AB//CD
C . ∵∠BCD+∠ADC=180°,∴AD//BC D . ∵∠CBA+∠C=180°,∴BC//AD
4.在如图形中若∠l=∠2,则可以使AB∥CD的是( )
A . B .
C . D .
5.如图,下列条件中能判定AB∥CD的是( )
A . ∠1=∠2 B . ∠2=∠4 C . ∠1=∠3 D . ∠B+∠BCD=180°
6.如图,下列条件不能判断直线a∥b的是( )
A . ∠1=∠4 B . ∠3=∠5 C . ∠2+∠5=180° D . ∠2+∠4=180°
7.下列命题正确的是( )
A . 相等的角是对顶角 B . 两条直线被第三条直线所截,同位角相等
C . 在同一平面内,垂直于一条直线的两条直线平行 D . 同旁内角互补
8.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于S,①AS=AR,②QP∥AR,③△BRP≌△QSP.其中正确的是( )
A . 全部正确 B . ①和② C . ① D . ②
9.如图,已知与上的点,点,小临同学现进行如下操作:以点为圆心,长为半径画弧,交于点,连接;以点为圆心,长为半径画弧,交于点;以点为圆心,长为半径画弧,交第步中所画的弧于点,连接下列结论不能由上述操作结果得出的是( )
A . B .
C . D .
10.如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
A . 数形结合 B . 特殊到一般 C . 一般到特殊 D . 转化
二、填空题
11.如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件有 _____.
12.如图,l∥m,等边△ABC的顶点A、B分别在直线l、m上,∠1=25°,则∠2=_____.
13.如图,要得到AB∥CD,只需要添加一个条件,这个条件可以是_____.(填一个你认为正确的条件即可)
14.
如果两条直线被第三条直线所截,一组同旁内角的度数比为3:2,差为36°,那么这两条直线的位置关系是_____ ,这是因为_____ .
三、解答题
15.已知:如图,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b.
16.如图,已知点C、F、E、B在一条直线上,CE=BF,DF = AE,∠CFD=∠BEA,写出CD与AB之间的关系,并证明你的结论.
17.如图,A、D、F、B在同一直线上,AD=BF,AE=BC,且AE∥BC.求证:
(1)△AEF≌△BCD;
(2)EF∥CD.
18.如图,已知 AB = CD, AE ^ BD, CF ^ BD, 垂足分别为 E, F , BF = DE, 求证 AB // CD .
一、选择题
1.下列四个图形中∠1=∠2,能够判定AB∥CD的是( )
A . B .
C . D .
2.如图,如果,那么,其依据可以简单说成( )
A . 两直线平行,内错角相等 B . 内错角相等,两直线平行
C . 两直线平行,同位角相等 D . 同位角相等,两直线平行
3.如图,下列推理中正确的是( )
A . ∵∠1=∠4, ∴BC//AD B . ∵∠2=∠3,∴AB//CD
C . ∵∠BCD+∠ADC=180°,∴AD//BC D . ∵∠CBA+∠C=180°,∴BC//AD
4.在如图形中若∠l=∠2,则可以使AB∥CD的是( )
A . B .
C . D .
5.如图,下列条件中能判定AB∥CD的是( )
A . ∠1=∠2 B . ∠2=∠4 C . ∠1=∠3 D . ∠B+∠BCD=180°
6.如图,下列条件不能判断直线a∥b的是( )
A . ∠1=∠4 B . ∠3=∠5 C . ∠2+∠5=180° D . ∠2+∠4=180°
7.下列命题正确的是( )
A . 相等的角是对顶角 B . 两条直线被第三条直线所截,同位角相等
C . 在同一平面内,垂直于一条直线的两条直线平行 D . 同旁内角互补
8.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于S,①AS=AR,②QP∥AR,③△BRP≌△QSP.其中正确的是( )
A . 全部正确 B . ①和② C . ① D . ②
9.如图,已知与上的点,点,小临同学现进行如下操作:以点为圆心,长为半径画弧,交于点,连接;以点为圆心,长为半径画弧,交于点;以点为圆心,长为半径画弧,交第步中所画的弧于点,连接下列结论不能由上述操作结果得出的是( )
A . B .
C . D .
10.如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
A . 数形结合 B . 特殊到一般 C . 一般到特殊 D . 转化
二、填空题
11.如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件有 _____.
12.如图,l∥m,等边△ABC的顶点A、B分别在直线l、m上,∠1=25°,则∠2=_____.
13.如图,要得到AB∥CD,只需要添加一个条件,这个条件可以是_____.(填一个你认为正确的条件即可)
14.
如果两条直线被第三条直线所截,一组同旁内角的度数比为3:2,差为36°,那么这两条直线的位置关系是_____ ,这是因为_____ .
三、解答题
15.已知:如图,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b.
16.如图,已知点C、F、E、B在一条直线上,CE=BF,DF = AE,∠CFD=∠BEA,写出CD与AB之间的关系,并证明你的结论.
17.如图,A、D、F、B在同一直线上,AD=BF,AE=BC,且AE∥BC.求证:
(1)△AEF≌△BCD;
(2)EF∥CD.
18.如图,已知 AB = CD, AE ^ BD, CF ^ BD, 垂足分别为 E, F , BF = DE, 求证 AB // CD .
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
