2023-2024学年青岛版数学九年级上册期末考试检测试卷(含答案)
文档属性
| 名称 | 2023-2024学年青岛版数学九年级上册期末考试检测试卷(含答案) | 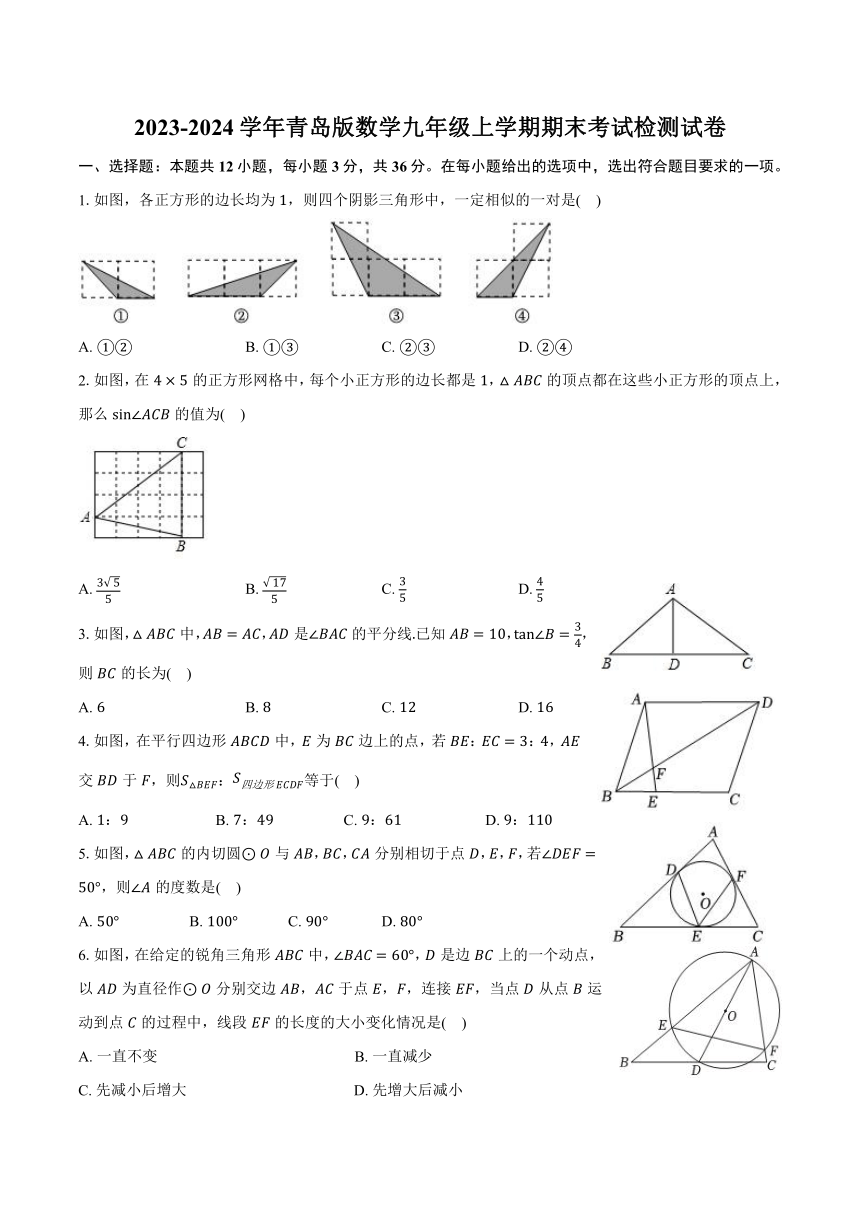 | |
| 格式 | docx | ||
| 文件大小 | 164.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 11:38:27 | ||
图片预览





文档简介
2023-2024学年青岛版数学九年级上学期期末考试检测试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,选出符合题目要求的一项。
1.如图,各正方形的边长均为,则四个阴影三角形中,一定相似的一对是( )
A. B. C. D.
2.如图,在的正方形网格中,每个小正方形的边长都是,的顶点都在这些小正方形的顶点上,那么的值为( )
A. B. C. D.
3.如图,中,,是的平分线已知,,则的长为( )
A. B. C. D.
4.如图,在平行四边形中,为边上的点,若::,交于,则:等于( )
A. : B. : C. : D. :
5.如图,的内切圆与,,分别相切于点,,,若,则的度数是( )
A. B. C. D.
6.如图,在给定的锐角三角形中,,是边上的一个动点,以为直径作分别交边,于点,,连接,当点从点运动到点的过程中,线段的长度的大小变化情况是( )
A. 一直不变 B. 一直减少
C. 先减小后增大 D. 先增大后减小
7.把方程配方,化成的形式应为( )
A. B. C. D.
8.已知关于的一元二次方程有两个实数根,的取值范围是( )
A. B. C. D.
9.如图,在直角坐标系中,点、、为某双曲线上不同的三点,连接、、,过点作轴于点,过点、分别作,轴于点、,与相交于点,记、、四边形的面积分别为、、,则( )
A. B.
C. D.
10.为了宣传环保,某学生写了一份倡议书在微博传播,规则为:将倡议书发表在自己的微博,再邀请个好友转发倡议书,每个好友转发倡议书,又邀请个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有人参与了传播活动,则方程列为( )
A. B.
C. D.
11.如图,已知是的直径,半径,点在劣弧上不与点,点重合,与交于点,设,,则以下关系式成立的是( )
A. B.
C. D.
12.如图,中,,,,将绕点逆时针旋转至,点在延长线上,则边扫过区域图中阴影部分的面积为( )
A. B.
C. D.
二、填空题:本题共5小题,每小题4分,共20分。
13.如图,为锐角三角形,是边上的高,正方形的一边在上,顶点,分别在,上已知,,则这个正方形的边长是______ .
14.如图,在矩形中,为上的点,,,则 .
(14题) (15题) (16题)
15.如图,为的直径,为的弦,,垂足为,,, ______ .
16.如图,与的边相切,切点为将绕点按顺时针方向旋转得到,使点落在上,边交线段于点若,则 ______ 度
17.在反比例函数的图象上,有一系列点,,,,,,若的横坐标为,以后每个点的横坐标与它前一个点的横坐标的差都为,过,,,,,分别作轴与轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分面积从左到右依次记为,,,,,则 ______ , ______ .
三、计算题:本大题共2小题,共14分。
18..
19.解方程:
;
四、解答题:本题共6小题,共58分。解答应写出文字说明,证明过程或演算步骤。
20.本小题分
已知关于的方程.
求证:无论取任意实数值,方程总有实数根;
若等腰的一边,另两边长、恰是这个方程的两个根,求的周长.
21.本小题分
如图,在平行四边形中,对角线、交于点,点为的中点,连接交于点,且.
求证:∽;
求的长;
若的面积为,求四边形的面积.
本小题分
如图,一座古塔座落在小山上塔顶记作点,其正下方水平面上的点记作点,小李站在附近的水平地面上,他想知道自己到古塔的水平距离,便利用无人机进行测量,但由于某些原因,无人机无法直接飞到塔顶进行测量,因此他先控制无人机从脚底记为点出发向右上方与地面成,点,,,在同一平面的方向匀速飞行秒到达空中点处,再调整飞行方向,继续匀速飞行秒到达塔顶,已知无人机的速度为米秒, 。
求小李到古塔的水平距离即的长结果精确到,参考数据:,
23.本小题分
如图,一次函数的图象与反比例函数的图象交于点,.
求函数的表达式;
根据图象写出使一次函数值大于反比例函数值时的取值范围;
点是反比例函数的图象上第一象限内的一个动点,当的面积等于的面积时,求点的坐标.
24.本小题分
杭州亚运会的三个吉祥物“琮琮”“宸宸”“莲莲”组合名为“江南忆”,出自唐朝诗人白居易的名句“江南忆,最忆是杭州”,它融合了杭州的历史人文、自然生态和创新基因吉祥物一开售,就深受大家的喜爱某商店以每件元的价格购进某款亚运会吉祥物,以每件的价格出售经统计,月份的销售量为件,月份的销售量为件.
求该款吉祥物月份到月份销售量的月平均增长率;
经市场预测,月份的销售量将与月份持平,现商场为了减少库存,采用降价促销方式,调查发现,该吉祥物每降价元,月销售量就会增加件当该吉祥物售价为多少元时,月销售利润达元?
25.本小题分
如图,中,,点为斜边的中点,以为直径作,分别与,边交于点,,连接,过点作,垂足为.
求证:是的切线;
已知的半径为,若,求的长.
九年级上学期期末考试检测试卷答案
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18. 解:
.
19. 解:,
,
则或,
解得:,;
,
,
,,,
,
,
,.
20. 证明:,
无论取任意实数值,方程总有实数根.
解:若,
方程有两个相等的实数根,
,
解得,
此时方程为,解得,
、、能够构成三角形,
的周长为;
若,则或,即方程有一根为,
把代入方程,得,
解得,
此时方程为,
解得,,
、、能够构成三角形,
的周长为;
综上所述,所求的周长为或.
21. 证明:四边形是平行四边形,
,
,,
∽;
∽,
,
为中点,
,即,
,
即,设,则有,,,
,
解得:,
;
∽,且相似比为:,
:::,
而的面积为,
,.
,
.
22. 解:过点作,交的延长线于点,过点作,垂足为,
由题意得:米,米,,,
,
,
,
在中,米,
在中,米,
米,
米,
小李到古塔的水平距离即的长约为米.
23. 解:一次函数的图象与反比例函数的图象交于点,,
,,
,
,,
,
;
由图象可知:
当或时,直线在双曲线上方,
一次函数值大于反比例函数值时的取值范围为:或;
的面积等于的面积,
点到直线的距离等于点到直线的距离,
将直线向上或向下平移个单位,得到直线,,直线,与双曲线在第一象限的交点即为点,
如图:
,
:,:,
联立,
解得:或不合题意,舍去;
;
联立,
解得:或不合题意,舍去;
;
综上:点的坐标为:或.
24. 解:设该款吉祥物月份到月份销售量的月平均增长率为,则月份的销售量为,
根据题意得:,
解得:,不符合题意,舍去,
答:该款吉祥物月份到月份销售量的月平均增长率为;
设该吉祥物售价为元,则每件的销售利润为元,月销售量为件,
根据题意得:,
整理得:,
解得:,不符合题意,舍去,
答:该款吉祥物售价为元时,月销售利润达元.
25. 证明:如图,连接,
在中,为边中点,
,
,
,
,
,
,
,
,
,
是的切线;
解:如图,连接,
是的直径,
,
,
四边形为矩形,
,
,
.
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,选出符合题目要求的一项。
1.如图,各正方形的边长均为,则四个阴影三角形中,一定相似的一对是( )
A. B. C. D.
2.如图,在的正方形网格中,每个小正方形的边长都是,的顶点都在这些小正方形的顶点上,那么的值为( )
A. B. C. D.
3.如图,中,,是的平分线已知,,则的长为( )
A. B. C. D.
4.如图,在平行四边形中,为边上的点,若::,交于,则:等于( )
A. : B. : C. : D. :
5.如图,的内切圆与,,分别相切于点,,,若,则的度数是( )
A. B. C. D.
6.如图,在给定的锐角三角形中,,是边上的一个动点,以为直径作分别交边,于点,,连接,当点从点运动到点的过程中,线段的长度的大小变化情况是( )
A. 一直不变 B. 一直减少
C. 先减小后增大 D. 先增大后减小
7.把方程配方,化成的形式应为( )
A. B. C. D.
8.已知关于的一元二次方程有两个实数根,的取值范围是( )
A. B. C. D.
9.如图,在直角坐标系中,点、、为某双曲线上不同的三点,连接、、,过点作轴于点,过点、分别作,轴于点、,与相交于点,记、、四边形的面积分别为、、,则( )
A. B.
C. D.
10.为了宣传环保,某学生写了一份倡议书在微博传播,规则为:将倡议书发表在自己的微博,再邀请个好友转发倡议书,每个好友转发倡议书,又邀请个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有人参与了传播活动,则方程列为( )
A. B.
C. D.
11.如图,已知是的直径,半径,点在劣弧上不与点,点重合,与交于点,设,,则以下关系式成立的是( )
A. B.
C. D.
12.如图,中,,,,将绕点逆时针旋转至,点在延长线上,则边扫过区域图中阴影部分的面积为( )
A. B.
C. D.
二、填空题:本题共5小题,每小题4分,共20分。
13.如图,为锐角三角形,是边上的高,正方形的一边在上,顶点,分别在,上已知,,则这个正方形的边长是______ .
14.如图,在矩形中,为上的点,,,则 .
(14题) (15题) (16题)
15.如图,为的直径,为的弦,,垂足为,,, ______ .
16.如图,与的边相切,切点为将绕点按顺时针方向旋转得到,使点落在上,边交线段于点若,则 ______ 度
17.在反比例函数的图象上,有一系列点,,,,,,若的横坐标为,以后每个点的横坐标与它前一个点的横坐标的差都为,过,,,,,分别作轴与轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分面积从左到右依次记为,,,,,则 ______ , ______ .
三、计算题:本大题共2小题,共14分。
18..
19.解方程:
;
四、解答题:本题共6小题,共58分。解答应写出文字说明,证明过程或演算步骤。
20.本小题分
已知关于的方程.
求证:无论取任意实数值,方程总有实数根;
若等腰的一边,另两边长、恰是这个方程的两个根,求的周长.
21.本小题分
如图,在平行四边形中,对角线、交于点,点为的中点,连接交于点,且.
求证:∽;
求的长;
若的面积为,求四边形的面积.
本小题分
如图,一座古塔座落在小山上塔顶记作点,其正下方水平面上的点记作点,小李站在附近的水平地面上,他想知道自己到古塔的水平距离,便利用无人机进行测量,但由于某些原因,无人机无法直接飞到塔顶进行测量,因此他先控制无人机从脚底记为点出发向右上方与地面成,点,,,在同一平面的方向匀速飞行秒到达空中点处,再调整飞行方向,继续匀速飞行秒到达塔顶,已知无人机的速度为米秒, 。
求小李到古塔的水平距离即的长结果精确到,参考数据:,
23.本小题分
如图,一次函数的图象与反比例函数的图象交于点,.
求函数的表达式;
根据图象写出使一次函数值大于反比例函数值时的取值范围;
点是反比例函数的图象上第一象限内的一个动点,当的面积等于的面积时,求点的坐标.
24.本小题分
杭州亚运会的三个吉祥物“琮琮”“宸宸”“莲莲”组合名为“江南忆”,出自唐朝诗人白居易的名句“江南忆,最忆是杭州”,它融合了杭州的历史人文、自然生态和创新基因吉祥物一开售,就深受大家的喜爱某商店以每件元的价格购进某款亚运会吉祥物,以每件的价格出售经统计,月份的销售量为件,月份的销售量为件.
求该款吉祥物月份到月份销售量的月平均增长率;
经市场预测,月份的销售量将与月份持平,现商场为了减少库存,采用降价促销方式,调查发现,该吉祥物每降价元,月销售量就会增加件当该吉祥物售价为多少元时,月销售利润达元?
25.本小题分
如图,中,,点为斜边的中点,以为直径作,分别与,边交于点,,连接,过点作,垂足为.
求证:是的切线;
已知的半径为,若,求的长.
九年级上学期期末考试检测试卷答案
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18. 解:
.
19. 解:,
,
则或,
解得:,;
,
,
,,,
,
,
,.
20. 证明:,
无论取任意实数值,方程总有实数根.
解:若,
方程有两个相等的实数根,
,
解得,
此时方程为,解得,
、、能够构成三角形,
的周长为;
若,则或,即方程有一根为,
把代入方程,得,
解得,
此时方程为,
解得,,
、、能够构成三角形,
的周长为;
综上所述,所求的周长为或.
21. 证明:四边形是平行四边形,
,
,,
∽;
∽,
,
为中点,
,即,
,
即,设,则有,,,
,
解得:,
;
∽,且相似比为:,
:::,
而的面积为,
,.
,
.
22. 解:过点作,交的延长线于点,过点作,垂足为,
由题意得:米,米,,,
,
,
,
在中,米,
在中,米,
米,
米,
小李到古塔的水平距离即的长约为米.
23. 解:一次函数的图象与反比例函数的图象交于点,,
,,
,
,,
,
;
由图象可知:
当或时,直线在双曲线上方,
一次函数值大于反比例函数值时的取值范围为:或;
的面积等于的面积,
点到直线的距离等于点到直线的距离,
将直线向上或向下平移个单位,得到直线,,直线,与双曲线在第一象限的交点即为点,
如图:
,
:,:,
联立,
解得:或不合题意,舍去;
;
联立,
解得:或不合题意,舍去;
;
综上:点的坐标为:或.
24. 解:设该款吉祥物月份到月份销售量的月平均增长率为,则月份的销售量为,
根据题意得:,
解得:,不符合题意,舍去,
答:该款吉祥物月份到月份销售量的月平均增长率为;
设该吉祥物售价为元,则每件的销售利润为元,月销售量为件,
根据题意得:,
整理得:,
解得:,不符合题意,舍去,
答:该款吉祥物售价为元时,月销售利润达元.
25. 证明:如图,连接,
在中,为边中点,
,
,
,
,
,
,
,
,
,
是的切线;
解:如图,连接,
是的直径,
,
,
四边形为矩形,
,
,
.
同课章节目录
