第一章全等三角形期末章节拔高练习2023-2024学年青岛版数学八年级上册(含答案)
文档属性
| 名称 | 第一章全等三角形期末章节拔高练习2023-2024学年青岛版数学八年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 436.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 00:00:00 | ||
图片预览


文档简介
青岛版数学八年级上册第一章全等三角形期末章节拔高练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.找出下列各组图中的全等图形( )
A.②和⑥ B.②和⑦ C.③和④ D.⑥和⑦
2.下列语句:①面积相等的两个三角形全等; ②两个等边三角形一定是全等图形;③如果两个三角形全等,它们的形状和大小一定都相同; ④边数相同的图形一定能互相重合.其中错误的说法有( )
A.4个 B.3个 C.2个 D.1个
3.如图,,且.、是上两点,,.若,,,则的长为( )
A. B. C. D.
4.下列各组条件中,能判定ΔABC≌ΔDEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠C=∠F,AC=EF
C.∠A=∠D,∠B=∠E,∠C=∠F D.AB=DE,BC=EF,ΔABC的周长=ΔDEF的周长
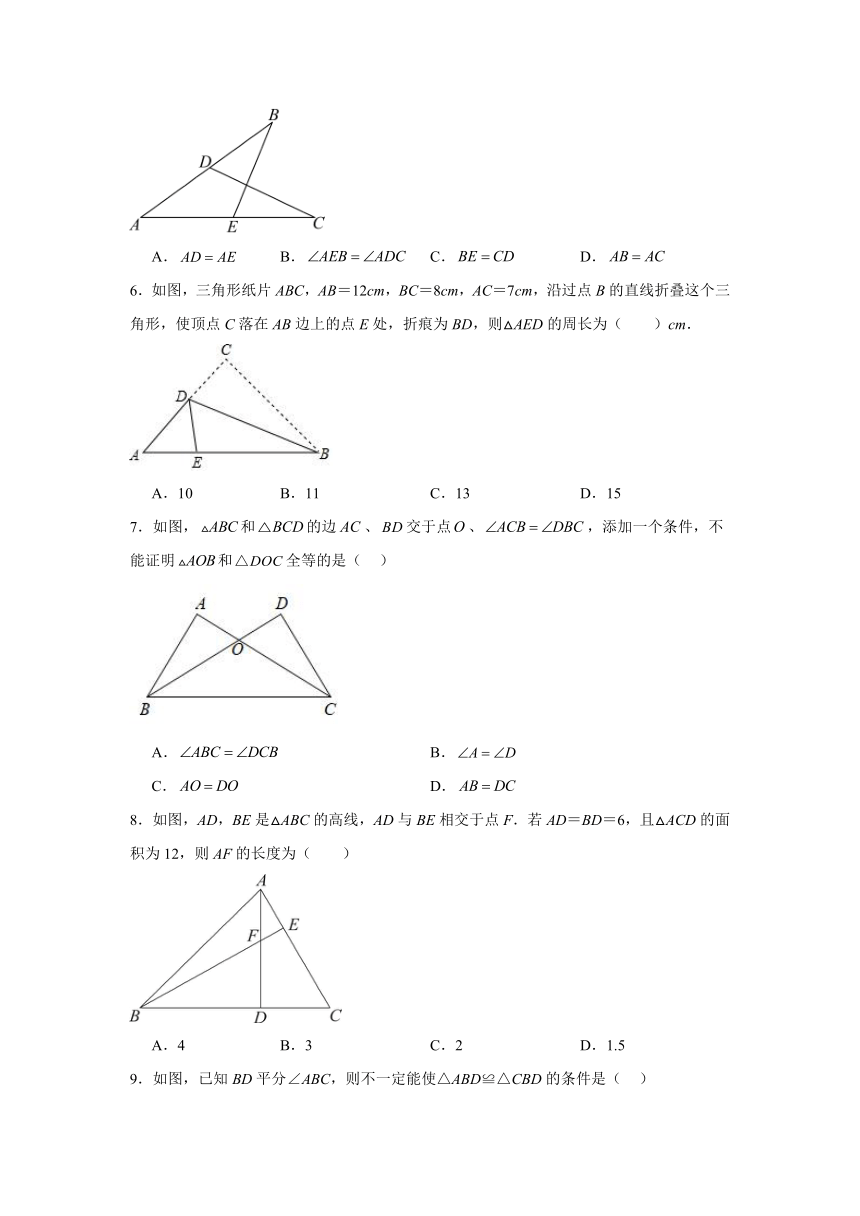
5.如图,D在上,E在上,且.补充下列一个条件后,仍无法判定的是( )
A. B. C. D.
6.如图,三角形纸片ABC,AB=12cm,BC=8cm,AC=7cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )cm.
A.10 B.11 C.13 D.15
7.如图,和的边、交于点、,添加一个条件,不能证明和全等的是( )
A. B.
C. D.
8.如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A.4 B.3 C.2 D.1.5
9.如图,已知BD平分∠ABC,则不一定能使△ABD≌△CBD的条件是( )
A.∠A=∠C B.∠ADB=∠CDB C.AB=CB D.AD=CD
10.如图,若,,,则的长为( )
A.2 B.3 C.4 D.5
二、填空题
11.如图,在中,,,C的坐标为,点A的坐标为,则点B的坐标为 .
12.如图,已知,.要证≌,还需添加的一个条件是 .
13.如图,已知,若要使△ABE≌△ACD,则还需添加一个条件; .
14.如图,,为的中点,于,于,图中全等三角形共有 对.
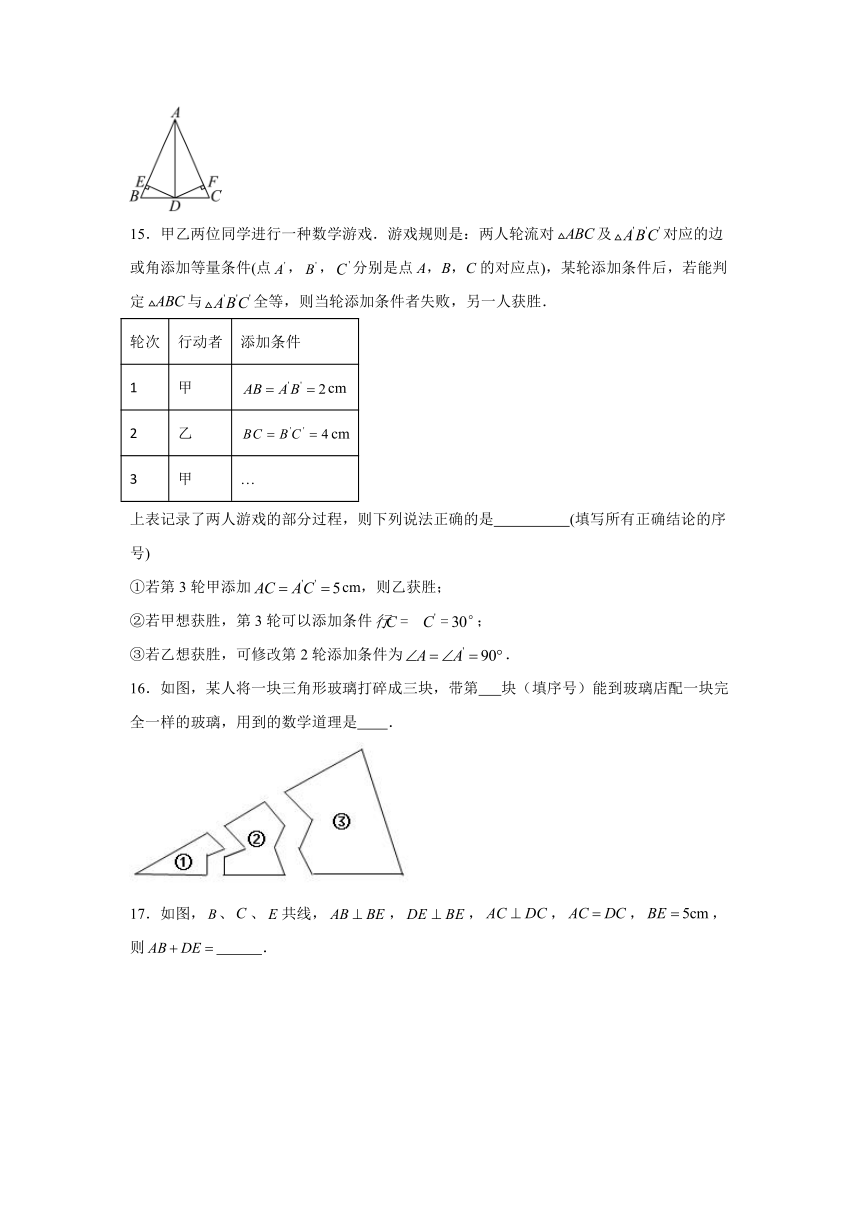
15.甲乙两位同学进行一种数学游戏.游戏规则是:两人轮流对及对应的边或角添加等量条件(点,,分别是点A,B,C的对应点),某轮添加条件后,若能判定与全等,则当轮添加条件者失败,另一人获胜.
轮次 行动者 添加条件
1 甲 cm
2 乙 cm
3 甲 …
上表记录了两人游戏的部分过程,则下列说法正确的是 (填写所有正确结论的序号)
①若第3轮甲添加cm,则乙获胜;
②若甲想获胜,第3轮可以添加条件;
③若乙想获胜,可修改第2轮添加条件为.
16.如图,某人将一块三角形玻璃打碎成三块,带第 块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是 .
17.如图,、、共线,,,,,,则 .
18.如图,直线l1与x轴、y轴分别交于,,直线l2经过点B且与x轴负半轴交于点C,,若线段上存在一点P,使是以A为直角顶点的等腰直角三角形,则P点坐标为 .
19.如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是 .
20.如图,在四边形ABCD中,AD=AB,DC=BC,∠DAB=60°,∠DCB=120°,E在AD上,F是AB延长线上一点,且DE=BF,若G在AB上,且∠ECG=60°,则DE、EG、BG之间的数量关系是 .
三、解答题
21.如图,在中() ,过点C作并连接,使,在上截取,连接.求证:.
22.如图,△ABC是等腰直角三角形,∠BCA=90°,BC=AC,直角顶点C在y轴上,锐角顶点A在x轴上.
(1)如图①,若点C的坐标是(0,﹣1),点A的坐标是(﹣3,0),求B点的坐标;
(2)如图②,若x轴恰好平分∠BAC,BC与x轴交于点D,过点B作BE⊥x轴于E,问AD与BE有怎样的数量关系,并说明理由;
(3)如图③,直角边AC在两坐标轴上滑动,使点B在第四象限内,过B点作BF⊥x轴于F,在滑动的过程中,猜想OC、BF、OA之间的关系,并证明你的结论.
23.如图,点D、E分别是AB、AC的中点,BE、CD相交于点O,∠B=∠C,BD=CE.求证:
(1)OD=OE;
(2)△ABE≌△ACD.
24.(1)计算:
(2)如图,点C是AB的中点,且AD=BE,CD=CE.求证:∠A=∠B.
25.(1)问题背景:
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC、CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小明同学探究此问题的方法是,延长FD到点G,使DG=BE,连接AG,先证明ABE≌ADG,再证明AEF≌AGF,可得出结论,他的结论应是 ;
(2)灵活运用:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,请说明理由;
(3)探索延伸:
如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,且满足EF=BE+FD,请直接写出∠EAF与∠DAB的数量关系.
参考答案:
1.C
2.B
3.D
4.D
5.B
6.B
7.D
8.C
9.D
10.A
11.
12.∠AEB=∠CFD
13.AB=AC或BE=CD或AD=AE
14.
15.①③
16. ③ ASA
17.5cm
18.
19.90°
20.DE+BG=EG
21.略
22.(1)B(1,2);(2)AD=2BE;(3)OC=BF+OA
23.略.
24.(1) (2)略
25.(1)BE+FD=EF;(2)BE+FD=EF仍然成立,(3)∠EAF=180°-∠DAB,
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.找出下列各组图中的全等图形( )
A.②和⑥ B.②和⑦ C.③和④ D.⑥和⑦
2.下列语句:①面积相等的两个三角形全等; ②两个等边三角形一定是全等图形;③如果两个三角形全等,它们的形状和大小一定都相同; ④边数相同的图形一定能互相重合.其中错误的说法有( )
A.4个 B.3个 C.2个 D.1个
3.如图,,且.、是上两点,,.若,,,则的长为( )
A. B. C. D.
4.下列各组条件中,能判定ΔABC≌ΔDEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠C=∠F,AC=EF
C.∠A=∠D,∠B=∠E,∠C=∠F D.AB=DE,BC=EF,ΔABC的周长=ΔDEF的周长
5.如图,D在上,E在上,且.补充下列一个条件后,仍无法判定的是( )
A. B. C. D.
6.如图,三角形纸片ABC,AB=12cm,BC=8cm,AC=7cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )cm.
A.10 B.11 C.13 D.15
7.如图,和的边、交于点、,添加一个条件,不能证明和全等的是( )
A. B.
C. D.
8.如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A.4 B.3 C.2 D.1.5
9.如图,已知BD平分∠ABC,则不一定能使△ABD≌△CBD的条件是( )
A.∠A=∠C B.∠ADB=∠CDB C.AB=CB D.AD=CD
10.如图,若,,,则的长为( )
A.2 B.3 C.4 D.5
二、填空题
11.如图,在中,,,C的坐标为,点A的坐标为,则点B的坐标为 .
12.如图,已知,.要证≌,还需添加的一个条件是 .
13.如图,已知,若要使△ABE≌△ACD,则还需添加一个条件; .
14.如图,,为的中点,于,于,图中全等三角形共有 对.
15.甲乙两位同学进行一种数学游戏.游戏规则是:两人轮流对及对应的边或角添加等量条件(点,,分别是点A,B,C的对应点),某轮添加条件后,若能判定与全等,则当轮添加条件者失败,另一人获胜.
轮次 行动者 添加条件
1 甲 cm
2 乙 cm
3 甲 …
上表记录了两人游戏的部分过程,则下列说法正确的是 (填写所有正确结论的序号)
①若第3轮甲添加cm,则乙获胜;
②若甲想获胜,第3轮可以添加条件;
③若乙想获胜,可修改第2轮添加条件为.
16.如图,某人将一块三角形玻璃打碎成三块,带第 块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是 .
17.如图,、、共线,,,,,,则 .
18.如图,直线l1与x轴、y轴分别交于,,直线l2经过点B且与x轴负半轴交于点C,,若线段上存在一点P,使是以A为直角顶点的等腰直角三角形,则P点坐标为 .
19.如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是 .
20.如图,在四边形ABCD中,AD=AB,DC=BC,∠DAB=60°,∠DCB=120°,E在AD上,F是AB延长线上一点,且DE=BF,若G在AB上,且∠ECG=60°,则DE、EG、BG之间的数量关系是 .
三、解答题
21.如图,在中() ,过点C作并连接,使,在上截取,连接.求证:.
22.如图,△ABC是等腰直角三角形,∠BCA=90°,BC=AC,直角顶点C在y轴上,锐角顶点A在x轴上.
(1)如图①,若点C的坐标是(0,﹣1),点A的坐标是(﹣3,0),求B点的坐标;
(2)如图②,若x轴恰好平分∠BAC,BC与x轴交于点D,过点B作BE⊥x轴于E,问AD与BE有怎样的数量关系,并说明理由;
(3)如图③,直角边AC在两坐标轴上滑动,使点B在第四象限内,过B点作BF⊥x轴于F,在滑动的过程中,猜想OC、BF、OA之间的关系,并证明你的结论.
23.如图,点D、E分别是AB、AC的中点,BE、CD相交于点O,∠B=∠C,BD=CE.求证:
(1)OD=OE;
(2)△ABE≌△ACD.
24.(1)计算:
(2)如图,点C是AB的中点,且AD=BE,CD=CE.求证:∠A=∠B.
25.(1)问题背景:
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC、CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小明同学探究此问题的方法是,延长FD到点G,使DG=BE,连接AG,先证明ABE≌ADG,再证明AEF≌AGF,可得出结论,他的结论应是 ;
(2)灵活运用:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,请说明理由;
(3)探索延伸:
如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,且满足EF=BE+FD,请直接写出∠EAF与∠DAB的数量关系.
参考答案:
1.C
2.B
3.D
4.D
5.B
6.B
7.D
8.C
9.D
10.A
11.
12.∠AEB=∠CFD
13.AB=AC或BE=CD或AD=AE
14.
15.①③
16. ③ ASA
17.5cm
18.
19.90°
20.DE+BG=EG
21.略
22.(1)B(1,2);(2)AD=2BE;(3)OC=BF+OA
23.略.
24.(1) (2)略
25.(1)BE+FD=EF;(2)BE+FD=EF仍然成立,(3)∠EAF=180°-∠DAB,
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
