湘教版初二数学期末总复习-几何部分
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
湘教版初二数学期末总复习——几何部分
一. 教学内容:
期末总复习——几何部分
二. 教学目标:
1. 通过复习,系统地了解本学期所学的几何知识,巩固和掌握三角形全等的性质与判定定理,并会灵活运用定理判定三角形全等,逐步训练学生用数学符号语言进行判断推理论证的能力。
2. 通过复习直角三角形的性质及勾股定理和直角三角形全等的判定,牢固掌握基本概念和性质定理及判定定理,解决较为复杂的几何问题,复习作三角形知识,巩固五种基本尺规作图,训练学生用作图语言表述数学问题,进一步培养学生分析、解决问题的能力。
三. 教学重点、难点、关键
重点:全等三角形的性质与三角形全等的判定。
难点:灵活选择三角形全等的判定定理,进行推理论证。
关键:会分析三角形中的边与角的关系来选择判定方法。
四. 方法指导:
1. 理解旋转定义可以从三个“一”下手,即“一个定点,一个方向,一个角度”。
2. 对生活中的图案,运用平移、旋转、轴对称的观点分析其形成过程,关键是在图案中找到“基本图案”,并运用平移、旋转、轴对称的组合进行变化、检验是否形成给出图案。
3. 找对应边、对应角常有以下六种方法:
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边。
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角。
(3)有公共边的,公共边是对应边。
(4)有公共角的,公共角是对应角。
(5)有对顶角的,对顶角是对应角。
(6)两个全等三角形中,一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角)。
4. 利用全等三角形证明线段相等或角相等的思路是:
(1)观察线段或角在哪两个可能全等的三角形中。
(2)分析要证全等的两个三角形,已知什么条件,还缺什么条件。
(3)设法得证所缺条件。
(4)当待证线段或角不分布在两个三角形中,可考虑添加辅助线。
5. 利用勾股定理解决问题须满足两个特征:
(1)在直角三角形中。
(2)已知两边,求第三边或第三边的平方。
用勾股定理计算线段的长,是勾股定理的一个重要应用,在没有现成的直角三角形时,要善于构造直角三角形。
6. 作图题的基本步骤一般有:已知、求作、作法等步骤。
已知事项中需写出并画出已知的图形。
求作事项中需写出求作什么图形及这个图形符合什么条件。
作法事项中需写出应用基本图形求作所作图形的过程,同时在图中保留基本作图痕迹。
7. 证明一般的两个三角形全等的方法有:SSS、SAS、ASA、AAS。
直角三角形除了上述方法外还有一种:HL。
【典型例题】
1. 复习旋转和图案设计:
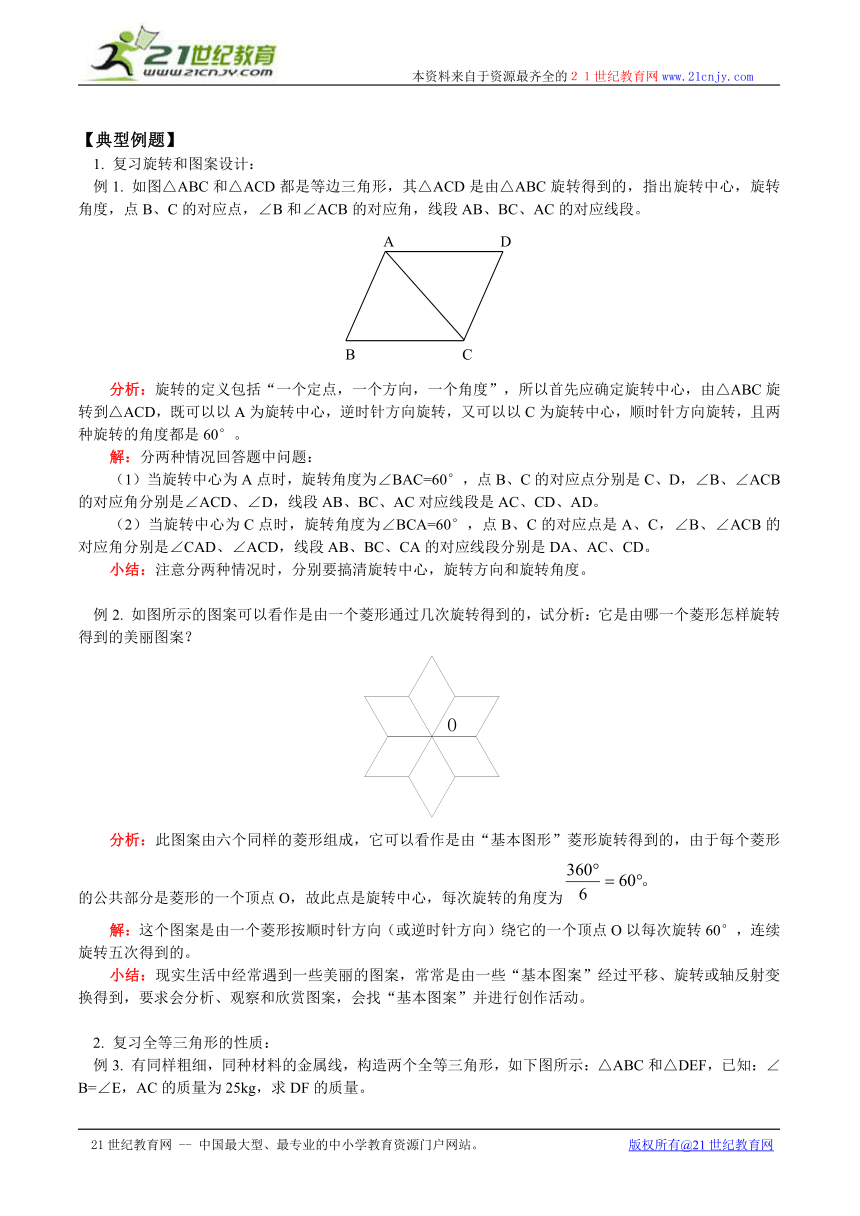
例1. 如图△ABC和△ACD都是等边三角形,其△ACD是由△ABC旋转得到的,指出旋转中心,旋转角度,点B、C的对应点,∠B和∠ACB的对应角,线段AB、BC、AC的对应线段。
分析:旋转的定义包括“一个定点,一个方向,一个角度”,所以首先应确定旋转中心,由△ABC旋转到△ACD,既可以以A为旋转中心,逆时针方向旋转,又可以以C为旋转中心,顺时针方向旋转,且两种旋转的角度都是60°。
解:分两种情况回答题中问题:
(1)当旋转中心为A点时,旋转角度为∠BAC=60°,点B、C的对应点分别是C、D,∠B、∠ACB的对应角分别是∠ACD、∠D,线段AB、BC、AC对应线段是AC、CD、AD。
(2)当旋转中心为C点时,旋转角度为∠BCA=60°,点B、C的对应点是A、C,∠B、∠ACB的对应角分别是∠CAD、∠ACD,线段AB、BC、CA的对应线段分别是DA、AC、CD。
小结:注意分两种情况时,分别要搞清旋转中心,旋转方向和旋转角度。
例2. 如图所示的图案可以看作是由一个菱形通过几次旋转得到的,试分析:它是由哪一个菱形怎样旋转得到的美丽图案?
分析:此图案由六个同样的菱形组成,它可以看作是由“基本图形”菱形旋转得到的,由于每个菱形的公共部分是菱形的一个顶点O,故此点是旋转中心,每次旋转的角度为
解:这个图案是由一个菱形按顺时针方向(或逆时针方向)绕它的一个顶点O以每次旋转60°,连续旋转五次得到的。
小结:现实生活中经常遇到一些美丽的图案,常常是由一些“基本图案”经过平移、旋转或轴反射变换得到,要求会分析、观察和欣赏图案,会找“基本图案”并进行创作活动。
2. 复习全等三角形的性质:
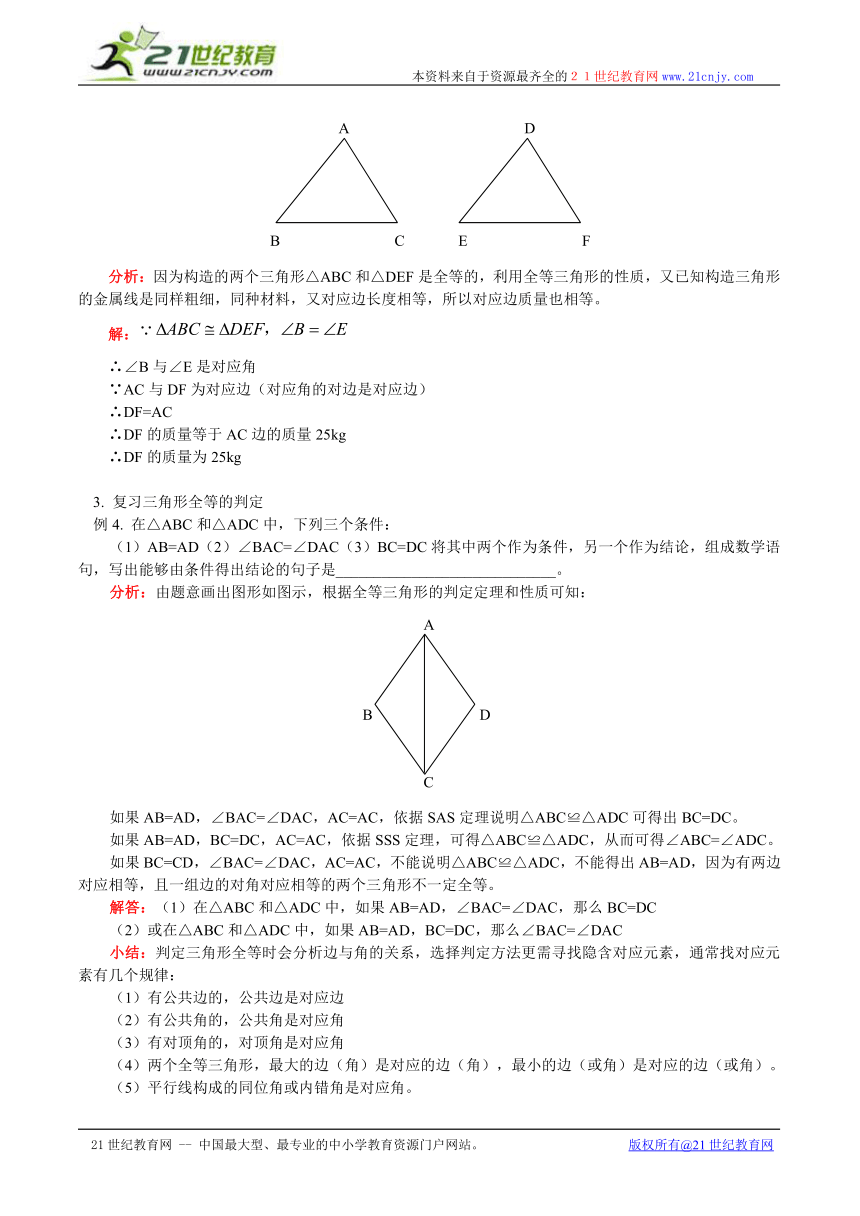
例3. 有同样粗细,同种材料的金属线,构造两个全等三角形,如下图所示:△ABC和△DEF,已知:∠B=∠E,AC的质量为25kg,求DF的质量。
分析:因为构造的两个三角形△ABC和△DEF是全等的,利用全等三角形的性质,又已知构造三角形的金属线是同样粗细,同种材料,又对应边长度相等,所以对应边质量也相等。
解:
∴∠B与∠E是对应角
∵AC与DF为对应边(对应角的对边是对应边)
∴DF=AC
∴DF的质量等于AC边的质量25kg
∴DF的质量为25kg
3. 复习三角形全等的判定
例4. 在△ABC和△ADC中,下列三个条件:
(1)AB=AD(2)∠BAC=∠DAC(3)BC=DC将其中两个作为条件,另一个作为结论,组成数学语句,写出能够由条件得出结论的句子是_____________________________。
分析:由题意画出图形如图示,根据全等三角形的判定定理和性质可知:
如果AB=AD,∠BAC=∠DAC,AC=AC,依据SAS定理说明△ABC≌△ADC可得出BC=DC。
如果AB=AD,BC=DC,AC=AC,依据SSS定理,可得△ABC≌△ADC,从而可得∠ABC=∠ADC。
如果BC=CD,∠BAC=∠DAC,AC=AC,不能说明△ABC≌△ADC,不能得出AB=AD,因为有两边对应相等,且一组边的对角对应相等的两个三角形不一定全等。
解答:(1)在△ABC和△ADC中,如果AB=AD,∠BAC=∠DAC,那么BC=DC
(2)或在△ABC和△ADC中,如果AB=AD,BC=DC,那么∠BAC=∠DAC
小结:判定三角形全等时会分析边与角的关系,选择判定方法更需寻找隐含对应元素,通常找对应元素有几个规律:
(1)有公共边的,公共边是对应边
(2)有公共角的,公共角是对应角
(3)有对顶角的,对顶角是对应角
(4)两个全等三角形,最大的边(角)是对应的边(角),最小的边(或角)是对应的边(或角)。
(5)平行线构成的同位角或内错角是对应角。
4. 复习直角三角形的判定与性质:
例5. 在△ABC中,AB=AC,BE⊥AC于E
求证:∠A=2∠1
分析1:本题是证明角的倍数问题,通常的方法是大角折半法,因此此题要证明的是∠A=2∠1,只需作出2∠1,或∠A,考虑到“AB=AC”,作BC边上的高AD问题便可迎刃而解。
证法1:作AD⊥BC于D
在Rt△ABD与Rt△ACD中
分析2:此题还可以利用小角加倍的方法证明角的倍数问题。
证法2:在AE上取点F,使EF=EC,
根据三角形的内角和定理:
5. 复习勾股定理:
例6. 如图甲,已知△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=2,求∠BPC的度数。
分析:此题是求∠BPC的度数,直接计算∠BPC比较困难,因此此题我们考虑用分角的方法,分出什么样的特殊角呢?我们通常是分出30°,45°,60°角这样的特殊角,此题我们考虑把∠BPC分割成有45°的特殊角的方法即作CE⊥PC,取CE=CP,即得∠CPE=45°,此时问题就转化到△PEB中,通过计算三边,判断是否为直角三角形,因PB=1已知,所以只需求出PE、EB的长度,再用勾股定理验证△PEB是否为直角三角形。
解:如图乙,过C作CE⊥CP,并截取CE=CP=2
连结BE、PE
∴△PBE为直角三角形
6. 复习作三角形
例7. 已知:线段a
求作:等腰直角三角形ABC,使BC=AC,AB=a
分析:先作草图,假设所求图形已作出,分析图形中的已知边与角对应的位置,并确定起始步骤作线段AB=a,但C的位置由已知条件无法直接得到,此时分析图形性质,等腰三角形底边上的高和中线重合,即点C在AB的垂直平分线上,且又由直角三角形斜边上的中线等于斜边的一半,故在AB的垂直平分线上可定出点C的位置,从而作出△ABC。
作法:
(1)作线段AB=a
(2)作线段AB的垂直平分线MN,交AB于O
∴△ABC即为所求作的三角形。
小结:综合作图题的步骤是由基本尺规作图组成,作图语言要求语句得当,语言规范,具有可操作性,不能想当然地写出作法。
7. 复分线的性质和判定
例8. 如图,在△ABC中,∠ABC=100°,∠ACB=20°,CE是∠ACB的平分线D是AC上一点,若∠CBD=20°,求∠ADE的度数。
分析:由已知条件∠ABC=100°,∠CBD=20°可以计算出∠ABD=80°,∠ABC的外角也是80°,即BA平分∠DBF,又CE平分∠ACB,故可过E作AC、BC及BD的垂线,由角平分线性质定理及逆定理可知DE平分∠ADB,又∠ADB=∠DCB+∠DBC=40°,从而可求出∠ADE的度数。
解:过E作EM⊥BD于M,EN⊥AD于N,EP⊥CB交CB的延长线于P。
∴EM=EP(角平分线上的点到这个角的两边的距离相等)
同理EP=EN
∴EM=EN(等量代换)
∴ED平分∠ADB(到一个角的两边距离相等的点在这个角的平分线上)
(三角形的一个外角等于与它不相邻的两个内角之和)
小结:解决本题的关键是添加辅助线,利用角平分线的性质及判定求解。
总结:本节课我们借助例题的形式复习了本学期所学过的几何部分的各个知识点,在复习的过程中我们还介绍了以下几种解决几何问题的相关方法:
(1)找全等三角形中对应元素的方法
(2)利用大角折半法和小角加倍法证明角的倍数问题
(3)利用分特殊角法求角的度数
(4)利用奠基法作三角形以及其它图形
(5)添加辅助线,利用角平分线的性质和判定
希望同学们在今后解决几何问题时,根据老师在以前的讲座和今天的讲座中所介绍的方法,灵活地运用这些方法,使自己的解题方法更巧妙,更灵活,思路更清晰。
【模拟试题】(满分100分,时间120分钟)
一. 填空题(每小题3分,共30分)
1. 的立方根的负倒数是__________。
2. 若a是的小数部分,b是的小数部分,则__________。
3. 已知一次函数的图象上有两点A(),B(),若,则,则k__________0。
4. 计算__________
5. 数轴上的点与__________是一一对应关系。
6. 一次函数与两坐标轴围成的三角形面积为__________。
7. 已知直角三角形一锐角是30°,斜边长为1,那么此直角三角形的周长是__________。
8. 已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为,则EF边上的高的长为__________cm。
9. 在中,斜边AB上的垂直平分线交直角边BC于D,交AB于E,且BC=4cm,AC=3cm,则△ADC的周长为__________cm。
10. 将一批数据分成5组,列出频率分布表,其中第一组的频率为0.2,第4组和第5组的频率之和是0.4,则第2组与第3组的频率之和为__________。
二. 选择题(每小题3分,共30分)
11. 若则的值是( )
A. 2或0 B. 2 C. 0 D. 以上答案都不对
12. 点P与Q(4,-6)关于x轴成轴反射,则P点的坐标是( )
A. (4,-6) B. (-4,-6) C. (4,6) D. (-4,6)
13. 要使成立,则m的取值( )
A. B. C. D. 一切实数
14. 某数的两个平方根是和,那么这个数是( )
A. 4 B. 7 C. –7 D. 49
15. ,则等于( )
A. –1 B. 0 C. 1 D. –5
16. 如图,线段AB的解析式是( )
A.
B.
C.
D.
17. 若函数,函数,且,则( )
A. y是x的正比例函数
B. y是x的一次函数
C. y不是x的正比例函数
D. y不是x的一次函数
18. 如图在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,则EB:EA=( )
A. 2:1 B. 3:1 C. 4:1 D. 5:1
19. 如图∠BAC=30°,P为∠BAC平分线上一点,PM//AC,PD⊥AC,如果AM=8cm,则PD等于( )
A. 2cm B. 3cm C. 4cm D. 5cm
20. 线段AB顺时针方向旋转90°到A’B’,则线段AB与线段A’B’的位置关系是( )
A. 互相垂直 B. 互相平行 C. 重合 D. 无法确定
三. 已知一斜边和一锐角,求作直角三角形(4分)
四. 计算题
(4分)
五. 解答题(每小题5分,共10分)
1. 一个一次函数的图象与直线的交点M的横坐标为2,与直线的交点N的纵坐标为1。
求:(1)这个一次函数的解析式。
(2)这个函数的图象与坐标轴围成的三角形的面积。
(3)用图象法求方程组的解。
2. △ABC中,∠C=90°,∠CAB=2∠B,AD平分∠CAB,,求DC的长。
六. 如图,已知,M是AC边中点,AD⊥BM交BC于D,交BM于E
求证:(8分)
七. 已知红鸟服装厂现有A种布料70m,B种布料52m,现计划用两种布料生产M、N两种型号的时装80套,已知做一套M型号的时装需用A种布料0.6m,B种布料0.9m,可获得利润45元,做一套N型号时装需用A种布料1.1m,B种布料0.4m,可获利润50元,若生产N型号的时装套数为x,用这批布料生产两种型号的时装所获得总利润y元,
(1)求y(元)与x(套)的函数关系式并求自变量x的取值范围。
(2)红鸟服装厂在生产这批时装中,当N型号的时装为多少套时所获利润最大?最大利润是多少?(8分)
八. 某校为了解一个年级的学习情况,在这个年级抽取50名学生,对某学科进行测试,将所得成绩(成绩均为整数)整理后,列出频率分布表如下表。
(1)这次测试80分以上的学生(包括80分)有多少?
(2)本次测试50名学生成绩的不及格率为多少?
(60分以下为不及格,不包括60分)
(3)画出频数分布直方图。
(4)你能从频数分布直方图中获取什么信息?(6分)
分组49.5~59.559.5~69.569.5~79.579.5~89.589.5~99.5 频率0.040.040.160.340.42
【试题答案】
一. 1. 2 2. 3. k<0
4. 5. 实数 6. 4.5
7. 8. 6 9. 7
10. 0.4
二. 11.
或0
∴选(A)。
12. C 13. D 14. D 15. A
16. A 17. A 18. B
19. 过P作PE⊥AB于E
∵AP是∠BAC的角平分线,PD⊥AC,PE⊥AB
∴PD=PE
∵在中,
∴选C
20. A
三. 略
四. 原式
五. 1. 设这个一次函数的解析式为:
∵这个一次函数的图象与直线的交点M的横坐标为2
∴M点的纵坐标为
∴M(2,5)
又∵它与的交点的纵坐标为1
∴N点的横坐标为:
∴N(1,1)
的图象经过M(2,5),N(1,1)
解之得:
∴一次函数的解析式为
(2)
解:与坐标轴的交点分别为A(,0),B(0,-3)
(3)图象略,其解为()
2.
解:
即
在中,
即
解之得
六. 证明:作∠BAC的角平分线交BM于G
∴在△AGB与△ADC中
在
七. 解:(1)
即
∵x取整数且
∴x取值为40,41,42,43,44
(2)当时,
y取最大值为3820元。
八. (2)人
(2)4% (3)略 (4)略
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
湘教版初二数学期末总复习——几何部分
一. 教学内容:
期末总复习——几何部分
二. 教学目标:
1. 通过复习,系统地了解本学期所学的几何知识,巩固和掌握三角形全等的性质与判定定理,并会灵活运用定理判定三角形全等,逐步训练学生用数学符号语言进行判断推理论证的能力。
2. 通过复习直角三角形的性质及勾股定理和直角三角形全等的判定,牢固掌握基本概念和性质定理及判定定理,解决较为复杂的几何问题,复习作三角形知识,巩固五种基本尺规作图,训练学生用作图语言表述数学问题,进一步培养学生分析、解决问题的能力。
三. 教学重点、难点、关键
重点:全等三角形的性质与三角形全等的判定。
难点:灵活选择三角形全等的判定定理,进行推理论证。
关键:会分析三角形中的边与角的关系来选择判定方法。
四. 方法指导:
1. 理解旋转定义可以从三个“一”下手,即“一个定点,一个方向,一个角度”。
2. 对生活中的图案,运用平移、旋转、轴对称的观点分析其形成过程,关键是在图案中找到“基本图案”,并运用平移、旋转、轴对称的组合进行变化、检验是否形成给出图案。
3. 找对应边、对应角常有以下六种方法:
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边。
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角。
(3)有公共边的,公共边是对应边。
(4)有公共角的,公共角是对应角。
(5)有对顶角的,对顶角是对应角。
(6)两个全等三角形中,一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角)。
4. 利用全等三角形证明线段相等或角相等的思路是:
(1)观察线段或角在哪两个可能全等的三角形中。
(2)分析要证全等的两个三角形,已知什么条件,还缺什么条件。
(3)设法得证所缺条件。
(4)当待证线段或角不分布在两个三角形中,可考虑添加辅助线。
5. 利用勾股定理解决问题须满足两个特征:
(1)在直角三角形中。
(2)已知两边,求第三边或第三边的平方。
用勾股定理计算线段的长,是勾股定理的一个重要应用,在没有现成的直角三角形时,要善于构造直角三角形。
6. 作图题的基本步骤一般有:已知、求作、作法等步骤。
已知事项中需写出并画出已知的图形。
求作事项中需写出求作什么图形及这个图形符合什么条件。
作法事项中需写出应用基本图形求作所作图形的过程,同时在图中保留基本作图痕迹。
7. 证明一般的两个三角形全等的方法有:SSS、SAS、ASA、AAS。
直角三角形除了上述方法外还有一种:HL。
【典型例题】
1. 复习旋转和图案设计:
例1. 如图△ABC和△ACD都是等边三角形,其△ACD是由△ABC旋转得到的,指出旋转中心,旋转角度,点B、C的对应点,∠B和∠ACB的对应角,线段AB、BC、AC的对应线段。
分析:旋转的定义包括“一个定点,一个方向,一个角度”,所以首先应确定旋转中心,由△ABC旋转到△ACD,既可以以A为旋转中心,逆时针方向旋转,又可以以C为旋转中心,顺时针方向旋转,且两种旋转的角度都是60°。
解:分两种情况回答题中问题:
(1)当旋转中心为A点时,旋转角度为∠BAC=60°,点B、C的对应点分别是C、D,∠B、∠ACB的对应角分别是∠ACD、∠D,线段AB、BC、AC对应线段是AC、CD、AD。
(2)当旋转中心为C点时,旋转角度为∠BCA=60°,点B、C的对应点是A、C,∠B、∠ACB的对应角分别是∠CAD、∠ACD,线段AB、BC、CA的对应线段分别是DA、AC、CD。
小结:注意分两种情况时,分别要搞清旋转中心,旋转方向和旋转角度。
例2. 如图所示的图案可以看作是由一个菱形通过几次旋转得到的,试分析:它是由哪一个菱形怎样旋转得到的美丽图案?
分析:此图案由六个同样的菱形组成,它可以看作是由“基本图形”菱形旋转得到的,由于每个菱形的公共部分是菱形的一个顶点O,故此点是旋转中心,每次旋转的角度为
解:这个图案是由一个菱形按顺时针方向(或逆时针方向)绕它的一个顶点O以每次旋转60°,连续旋转五次得到的。
小结:现实生活中经常遇到一些美丽的图案,常常是由一些“基本图案”经过平移、旋转或轴反射变换得到,要求会分析、观察和欣赏图案,会找“基本图案”并进行创作活动。
2. 复习全等三角形的性质:
例3. 有同样粗细,同种材料的金属线,构造两个全等三角形,如下图所示:△ABC和△DEF,已知:∠B=∠E,AC的质量为25kg,求DF的质量。
分析:因为构造的两个三角形△ABC和△DEF是全等的,利用全等三角形的性质,又已知构造三角形的金属线是同样粗细,同种材料,又对应边长度相等,所以对应边质量也相等。
解:
∴∠B与∠E是对应角
∵AC与DF为对应边(对应角的对边是对应边)
∴DF=AC
∴DF的质量等于AC边的质量25kg
∴DF的质量为25kg
3. 复习三角形全等的判定
例4. 在△ABC和△ADC中,下列三个条件:
(1)AB=AD(2)∠BAC=∠DAC(3)BC=DC将其中两个作为条件,另一个作为结论,组成数学语句,写出能够由条件得出结论的句子是_____________________________。
分析:由题意画出图形如图示,根据全等三角形的判定定理和性质可知:
如果AB=AD,∠BAC=∠DAC,AC=AC,依据SAS定理说明△ABC≌△ADC可得出BC=DC。
如果AB=AD,BC=DC,AC=AC,依据SSS定理,可得△ABC≌△ADC,从而可得∠ABC=∠ADC。
如果BC=CD,∠BAC=∠DAC,AC=AC,不能说明△ABC≌△ADC,不能得出AB=AD,因为有两边对应相等,且一组边的对角对应相等的两个三角形不一定全等。
解答:(1)在△ABC和△ADC中,如果AB=AD,∠BAC=∠DAC,那么BC=DC
(2)或在△ABC和△ADC中,如果AB=AD,BC=DC,那么∠BAC=∠DAC
小结:判定三角形全等时会分析边与角的关系,选择判定方法更需寻找隐含对应元素,通常找对应元素有几个规律:
(1)有公共边的,公共边是对应边
(2)有公共角的,公共角是对应角
(3)有对顶角的,对顶角是对应角
(4)两个全等三角形,最大的边(角)是对应的边(角),最小的边(或角)是对应的边(或角)。
(5)平行线构成的同位角或内错角是对应角。
4. 复习直角三角形的判定与性质:
例5. 在△ABC中,AB=AC,BE⊥AC于E
求证:∠A=2∠1
分析1:本题是证明角的倍数问题,通常的方法是大角折半法,因此此题要证明的是∠A=2∠1,只需作出2∠1,或∠A,考虑到“AB=AC”,作BC边上的高AD问题便可迎刃而解。
证法1:作AD⊥BC于D
在Rt△ABD与Rt△ACD中
分析2:此题还可以利用小角加倍的方法证明角的倍数问题。
证法2:在AE上取点F,使EF=EC,
根据三角形的内角和定理:
5. 复习勾股定理:
例6. 如图甲,已知△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=2,求∠BPC的度数。
分析:此题是求∠BPC的度数,直接计算∠BPC比较困难,因此此题我们考虑用分角的方法,分出什么样的特殊角呢?我们通常是分出30°,45°,60°角这样的特殊角,此题我们考虑把∠BPC分割成有45°的特殊角的方法即作CE⊥PC,取CE=CP,即得∠CPE=45°,此时问题就转化到△PEB中,通过计算三边,判断是否为直角三角形,因PB=1已知,所以只需求出PE、EB的长度,再用勾股定理验证△PEB是否为直角三角形。
解:如图乙,过C作CE⊥CP,并截取CE=CP=2
连结BE、PE
∴△PBE为直角三角形
6. 复习作三角形
例7. 已知:线段a
求作:等腰直角三角形ABC,使BC=AC,AB=a
分析:先作草图,假设所求图形已作出,分析图形中的已知边与角对应的位置,并确定起始步骤作线段AB=a,但C的位置由已知条件无法直接得到,此时分析图形性质,等腰三角形底边上的高和中线重合,即点C在AB的垂直平分线上,且又由直角三角形斜边上的中线等于斜边的一半,故在AB的垂直平分线上可定出点C的位置,从而作出△ABC。
作法:
(1)作线段AB=a
(2)作线段AB的垂直平分线MN,交AB于O
∴△ABC即为所求作的三角形。
小结:综合作图题的步骤是由基本尺规作图组成,作图语言要求语句得当,语言规范,具有可操作性,不能想当然地写出作法。
7. 复分线的性质和判定
例8. 如图,在△ABC中,∠ABC=100°,∠ACB=20°,CE是∠ACB的平分线D是AC上一点,若∠CBD=20°,求∠ADE的度数。
分析:由已知条件∠ABC=100°,∠CBD=20°可以计算出∠ABD=80°,∠ABC的外角也是80°,即BA平分∠DBF,又CE平分∠ACB,故可过E作AC、BC及BD的垂线,由角平分线性质定理及逆定理可知DE平分∠ADB,又∠ADB=∠DCB+∠DBC=40°,从而可求出∠ADE的度数。
解:过E作EM⊥BD于M,EN⊥AD于N,EP⊥CB交CB的延长线于P。
∴EM=EP(角平分线上的点到这个角的两边的距离相等)
同理EP=EN
∴EM=EN(等量代换)
∴ED平分∠ADB(到一个角的两边距离相等的点在这个角的平分线上)
(三角形的一个外角等于与它不相邻的两个内角之和)
小结:解决本题的关键是添加辅助线,利用角平分线的性质及判定求解。
总结:本节课我们借助例题的形式复习了本学期所学过的几何部分的各个知识点,在复习的过程中我们还介绍了以下几种解决几何问题的相关方法:
(1)找全等三角形中对应元素的方法
(2)利用大角折半法和小角加倍法证明角的倍数问题
(3)利用分特殊角法求角的度数
(4)利用奠基法作三角形以及其它图形
(5)添加辅助线,利用角平分线的性质和判定
希望同学们在今后解决几何问题时,根据老师在以前的讲座和今天的讲座中所介绍的方法,灵活地运用这些方法,使自己的解题方法更巧妙,更灵活,思路更清晰。
【模拟试题】(满分100分,时间120分钟)
一. 填空题(每小题3分,共30分)
1. 的立方根的负倒数是__________。
2. 若a是的小数部分,b是的小数部分,则__________。
3. 已知一次函数的图象上有两点A(),B(),若,则,则k__________0。
4. 计算__________
5. 数轴上的点与__________是一一对应关系。
6. 一次函数与两坐标轴围成的三角形面积为__________。
7. 已知直角三角形一锐角是30°,斜边长为1,那么此直角三角形的周长是__________。
8. 已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为,则EF边上的高的长为__________cm。
9. 在中,斜边AB上的垂直平分线交直角边BC于D,交AB于E,且BC=4cm,AC=3cm,则△ADC的周长为__________cm。
10. 将一批数据分成5组,列出频率分布表,其中第一组的频率为0.2,第4组和第5组的频率之和是0.4,则第2组与第3组的频率之和为__________。
二. 选择题(每小题3分,共30分)
11. 若则的值是( )
A. 2或0 B. 2 C. 0 D. 以上答案都不对
12. 点P与Q(4,-6)关于x轴成轴反射,则P点的坐标是( )
A. (4,-6) B. (-4,-6) C. (4,6) D. (-4,6)
13. 要使成立,则m的取值( )
A. B. C. D. 一切实数
14. 某数的两个平方根是和,那么这个数是( )
A. 4 B. 7 C. –7 D. 49
15. ,则等于( )
A. –1 B. 0 C. 1 D. –5
16. 如图,线段AB的解析式是( )
A.
B.
C.
D.
17. 若函数,函数,且,则( )
A. y是x的正比例函数
B. y是x的一次函数
C. y不是x的正比例函数
D. y不是x的一次函数
18. 如图在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,则EB:EA=( )
A. 2:1 B. 3:1 C. 4:1 D. 5:1
19. 如图∠BAC=30°,P为∠BAC平分线上一点,PM//AC,PD⊥AC,如果AM=8cm,则PD等于( )
A. 2cm B. 3cm C. 4cm D. 5cm
20. 线段AB顺时针方向旋转90°到A’B’,则线段AB与线段A’B’的位置关系是( )
A. 互相垂直 B. 互相平行 C. 重合 D. 无法确定
三. 已知一斜边和一锐角,求作直角三角形(4分)
四. 计算题
(4分)
五. 解答题(每小题5分,共10分)
1. 一个一次函数的图象与直线的交点M的横坐标为2,与直线的交点N的纵坐标为1。
求:(1)这个一次函数的解析式。
(2)这个函数的图象与坐标轴围成的三角形的面积。
(3)用图象法求方程组的解。
2. △ABC中,∠C=90°,∠CAB=2∠B,AD平分∠CAB,,求DC的长。
六. 如图,已知,M是AC边中点,AD⊥BM交BC于D,交BM于E
求证:(8分)
七. 已知红鸟服装厂现有A种布料70m,B种布料52m,现计划用两种布料生产M、N两种型号的时装80套,已知做一套M型号的时装需用A种布料0.6m,B种布料0.9m,可获得利润45元,做一套N型号时装需用A种布料1.1m,B种布料0.4m,可获利润50元,若生产N型号的时装套数为x,用这批布料生产两种型号的时装所获得总利润y元,
(1)求y(元)与x(套)的函数关系式并求自变量x的取值范围。
(2)红鸟服装厂在生产这批时装中,当N型号的时装为多少套时所获利润最大?最大利润是多少?(8分)
八. 某校为了解一个年级的学习情况,在这个年级抽取50名学生,对某学科进行测试,将所得成绩(成绩均为整数)整理后,列出频率分布表如下表。
(1)这次测试80分以上的学生(包括80分)有多少?
(2)本次测试50名学生成绩的不及格率为多少?
(60分以下为不及格,不包括60分)
(3)画出频数分布直方图。
(4)你能从频数分布直方图中获取什么信息?(6分)
分组49.5~59.559.5~69.569.5~79.579.5~89.589.5~99.5 频率0.040.040.160.340.42
【试题答案】
一. 1. 2 2. 3. k<0
4. 5. 实数 6. 4.5
7. 8. 6 9. 7
10. 0.4
二. 11.
或0
∴选(A)。
12. C 13. D 14. D 15. A
16. A 17. A 18. B
19. 过P作PE⊥AB于E
∵AP是∠BAC的角平分线,PD⊥AC,PE⊥AB
∴PD=PE
∵在中,
∴选C
20. A
三. 略
四. 原式
五. 1. 设这个一次函数的解析式为:
∵这个一次函数的图象与直线的交点M的横坐标为2
∴M点的纵坐标为
∴M(2,5)
又∵它与的交点的纵坐标为1
∴N点的横坐标为:
∴N(1,1)
的图象经过M(2,5),N(1,1)
解之得:
∴一次函数的解析式为
(2)
解:与坐标轴的交点分别为A(,0),B(0,-3)
(3)图象略,其解为()
2.
解:
即
在中,
即
解之得
六. 证明:作∠BAC的角平分线交BM于G
∴在△AGB与△ADC中
在
七. 解:(1)
即
∵x取整数且
∴x取值为40,41,42,43,44
(2)当时,
y取最大值为3820元。
八. (2)人
(2)4% (3)略 (4)略
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
