6.4.3 余弦定理、正弦定理 第3课时 课件(共17张PPT)
文档属性
| 名称 | 6.4.3 余弦定理、正弦定理 第3课时 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 757.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 16:59:13 | ||
图片预览






文档简介
(共17张PPT)
6.4.3 余弦定理、正弦定理 第3课时
1.掌握应用正弦定理、余弦定理解决实际问题的基本分析方法和步骤
2.能用正弦定理和余弦定理解决距离问题
人类第一次登上月球是1969年,而在1671年,两位法国天文学家却已经测量出了地球与月球之间的距离为385 400km,在不可到达月球的情况下,天文学家如何测量地球与月亮之间的距离
导入
知识点1:距离问题
1.定义
在测量过程中,我们把根据测量的需要而确定的线段叫做基线.
2.性质
在测量过程中,应根据实际需要选取合适的基线长度,使测量具有
较高的精确度.一般来说,基线越长,测量的精确度越高.
例1:A,B两点都在河的对岸(不可到达),设计一种测量A,B两点间距离的方法.并求出A,B的距离.
分析:若测量者在A,B两点的对岸取定一点C,则在点C处只能测出∠ACB的大小,因而无法解决问題.
可再取一点D,测出线段CD的长,以及∠ACD,
∠CDB,∠BDA,这样就可借助正弦定理和余弦定理算出距离.
解:在河岸边选定两点C、D,设CD=a,∠BCA=α,∠ACD=β,∠CDB=γ,∠ADB=δ
在△ADC和△BDC中,由正弦定理,得
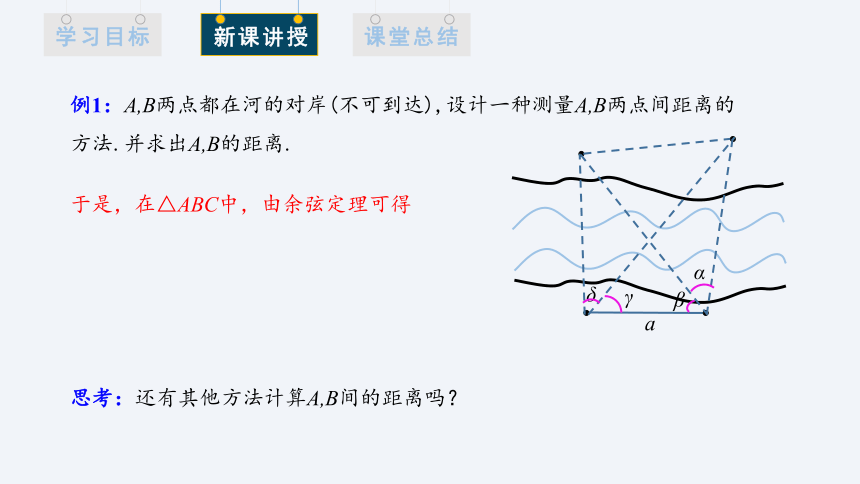
例1:A,B两点都在河的对岸(不可到达),设计一种测量A,B两点间距离的方法.并求出A,B的距离.
β
α
γ
a
δ
于是,在△ABC中,由余弦定理可得
β
α
δ
γ
例1:A,B两点都在河的对岸(不可到达),设计一种测量A,B两点间距离的方法.并求出A,B的距离.
思考:还有其他方法计算A,B间的距离吗?
a
测量距离的基本类型及方案
类型 A,B两点间不可达 A,B两点可视,但有一点不可达 A,B两点可都不可达
图形
方法
先测角C, AC=b, BC=a,再用余弦定理求AB
以点A不可达为例,先测角B,C,BC=a,再用正弦定理求AB
测得CD=a,∠BCD,∠BDC,
∠ACD,∠ADC,∠ACB,在△ACD中用正弦定理求AC;在△BCD中用正弦定理求BC;
在△ABC中用余弦定理求AB
1.坡度:
知识点2:高度问题
2.仰角和俯角:
在视线和水平线所成的角中,视线在水平线上方的角叫仰角,
视线在水平线下方的角叫俯角.
斜面与地平面所成的角度
例2:AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法,求出建筑物的高度.
分析:只要获得一点C (点C到地面的距离可求)到建筑物的顶部A的距离CA,并测出由点C观察A的仰角,就可以计算出建筑物的高度.
再选取一点D,构造另一个含有CA的△ACD,并进行相关的长度和角度的测量,然后通过解三角形的方法计算出CA.
C
D
例2:AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法,求出建筑物的高度.
解:选择一条水平基线HG,使H,G,B三点在同一条直线上.由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.
C
α
D
β
G
H
a
在△ACD中,根据正弦定理可得
h
类型 简图 计算方法
底部可达
底部 不可达 点B与C,D共线
点B与C,D不共线
测得CD=a及∠BCD,∠BDC,∠ACB的度数.
在△BCD中由正弦定理求得BC,再解三角形得AB的值.
测得CD=a及C与∠ADB的度数.
先由正弦定理求出AC或AD,再解三角形得AB的值.
测得BC=a,∠BCA=C,AB=a·tanC
在解决关于角度测量的问题时,需要明确以下几个概念:
知识点3:角度问题
1.方位角
从某点的指北方向线顺时针方向至目标方向线间的水平夹角.
从正北或正南方向到目标方向所形成的小于90°的角.
2.方向角
北
南
东
西
A
α
B
β
例3:位于某海域A处的甲船获悉,在其正东方向相距20 n mile的B处有一艘渔船遇险后抛锚等待营救.甲船立即前往救援,同时把消息告知位于甲船南偏西30°,且与甲船相距7 n mile的C处的乙船.那么乙船前往营救遇险渔船时的目标方向线(由观测点看目标的视线)的方向是北偏东多少度(精确到1°) 需要航行的距离是多少海里(精确到1n mile)
解:画岀示意图
北
C
B
A
由余弦定理,得
7 n mile
20 n mile
30°
于是
北
C
B
A
由正弦定理,得
7 n mile
20 n mile
30°
于是
由于 0°因此,乙船前往营救遇险渔船时的方向约是北偏东46° + 30° = 76°,
大约需要航行24 n mile.
运用正、余弦定理解决实际问题的基本步骤
(1)分析:理解题意,弄清已知与未知,画出示意图(一个或几个三角形);
(2)建模:根据已知条件与求解目标,把已知量与待求量尽可能地集中在有关三角形中,建立一个解三角形的数学模型;
(3)求解:利用正弦定理、余弦定理解三角形,求得数学模型的解;
(4)检验:检验所求的解是否符合实际问题,从而得出实际问题的解.
归纳总结
要点概括整合
余弦定理、正弦定理的实际应用
测量距离
测量角度
测量高度
仰角
方向角
方位角
俯角
基点
基线
解决实际问题的步骤
6.4.3 余弦定理、正弦定理 第3课时
1.掌握应用正弦定理、余弦定理解决实际问题的基本分析方法和步骤
2.能用正弦定理和余弦定理解决距离问题
人类第一次登上月球是1969年,而在1671年,两位法国天文学家却已经测量出了地球与月球之间的距离为385 400km,在不可到达月球的情况下,天文学家如何测量地球与月亮之间的距离
导入
知识点1:距离问题
1.定义
在测量过程中,我们把根据测量的需要而确定的线段叫做基线.
2.性质
在测量过程中,应根据实际需要选取合适的基线长度,使测量具有
较高的精确度.一般来说,基线越长,测量的精确度越高.
例1:A,B两点都在河的对岸(不可到达),设计一种测量A,B两点间距离的方法.并求出A,B的距离.
分析:若测量者在A,B两点的对岸取定一点C,则在点C处只能测出∠ACB的大小,因而无法解决问題.
可再取一点D,测出线段CD的长,以及∠ACD,
∠CDB,∠BDA,这样就可借助正弦定理和余弦定理算出距离.
解:在河岸边选定两点C、D,设CD=a,∠BCA=α,∠ACD=β,∠CDB=γ,∠ADB=δ
在△ADC和△BDC中,由正弦定理,得
例1:A,B两点都在河的对岸(不可到达),设计一种测量A,B两点间距离的方法.并求出A,B的距离.
β
α
γ
a
δ
于是,在△ABC中,由余弦定理可得
β
α
δ
γ
例1:A,B两点都在河的对岸(不可到达),设计一种测量A,B两点间距离的方法.并求出A,B的距离.
思考:还有其他方法计算A,B间的距离吗?
a
测量距离的基本类型及方案
类型 A,B两点间不可达 A,B两点可视,但有一点不可达 A,B两点可都不可达
图形
方法
先测角C, AC=b, BC=a,再用余弦定理求AB
以点A不可达为例,先测角B,C,BC=a,再用正弦定理求AB
测得CD=a,∠BCD,∠BDC,
∠ACD,∠ADC,∠ACB,在△ACD中用正弦定理求AC;在△BCD中用正弦定理求BC;
在△ABC中用余弦定理求AB
1.坡度:
知识点2:高度问题
2.仰角和俯角:
在视线和水平线所成的角中,视线在水平线上方的角叫仰角,
视线在水平线下方的角叫俯角.
斜面与地平面所成的角度
例2:AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法,求出建筑物的高度.
分析:只要获得一点C (点C到地面的距离可求)到建筑物的顶部A的距离CA,并测出由点C观察A的仰角,就可以计算出建筑物的高度.
再选取一点D,构造另一个含有CA的△ACD,并进行相关的长度和角度的测量,然后通过解三角形的方法计算出CA.
C
D
例2:AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法,求出建筑物的高度.
解:选择一条水平基线HG,使H,G,B三点在同一条直线上.由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.
C
α
D
β
G
H
a
在△ACD中,根据正弦定理可得
h
类型 简图 计算方法
底部可达
底部 不可达 点B与C,D共线
点B与C,D不共线
测得CD=a及∠BCD,∠BDC,∠ACB的度数.
在△BCD中由正弦定理求得BC,再解三角形得AB的值.
测得CD=a及C与∠ADB的度数.
先由正弦定理求出AC或AD,再解三角形得AB的值.
测得BC=a,∠BCA=C,AB=a·tanC
在解决关于角度测量的问题时,需要明确以下几个概念:
知识点3:角度问题
1.方位角
从某点的指北方向线顺时针方向至目标方向线间的水平夹角.
从正北或正南方向到目标方向所形成的小于90°的角.
2.方向角
北
南
东
西
A
α
B
β
例3:位于某海域A处的甲船获悉,在其正东方向相距20 n mile的B处有一艘渔船遇险后抛锚等待营救.甲船立即前往救援,同时把消息告知位于甲船南偏西30°,且与甲船相距7 n mile的C处的乙船.那么乙船前往营救遇险渔船时的目标方向线(由观测点看目标的视线)的方向是北偏东多少度(精确到1°) 需要航行的距离是多少海里(精确到1n mile)
解:画岀示意图
北
C
B
A
由余弦定理,得
7 n mile
20 n mile
30°
于是
北
C
B
A
由正弦定理,得
7 n mile
20 n mile
30°
于是
由于 0°
大约需要航行24 n mile.
运用正、余弦定理解决实际问题的基本步骤
(1)分析:理解题意,弄清已知与未知,画出示意图(一个或几个三角形);
(2)建模:根据已知条件与求解目标,把已知量与待求量尽可能地集中在有关三角形中,建立一个解三角形的数学模型;
(3)求解:利用正弦定理、余弦定理解三角形,求得数学模型的解;
(4)检验:检验所求的解是否符合实际问题,从而得出实际问题的解.
归纳总结
要点概括整合
余弦定理、正弦定理的实际应用
测量距离
测量角度
测量高度
仰角
方向角
方位角
俯角
基点
基线
解决实际问题的步骤
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
