8.4.2 空间点、直线、平面之间的位置关系 课件(共16张PPT)
文档属性
| 名称 | 8.4.2 空间点、直线、平面之间的位置关系 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 619.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 18:05:00 | ||
图片预览




文档简介
(共16张PPT)
8.4.2 空间点、直线、平面之间的位置关系
1.了解空间中两条直线间的位置关系,理解异面直线的定义
2.了解直线与平面之间的三种位置关系,并能判断直线与平面的位置关系,会用符号语言和图形语言表示
3.了解平面与平面之间的两种位置关系,会用符号语言和图形语言表示
在同一平面内,两条直线有几种位置关系?空间中两条直线有没有其他的位置关系?
直线在同一平面
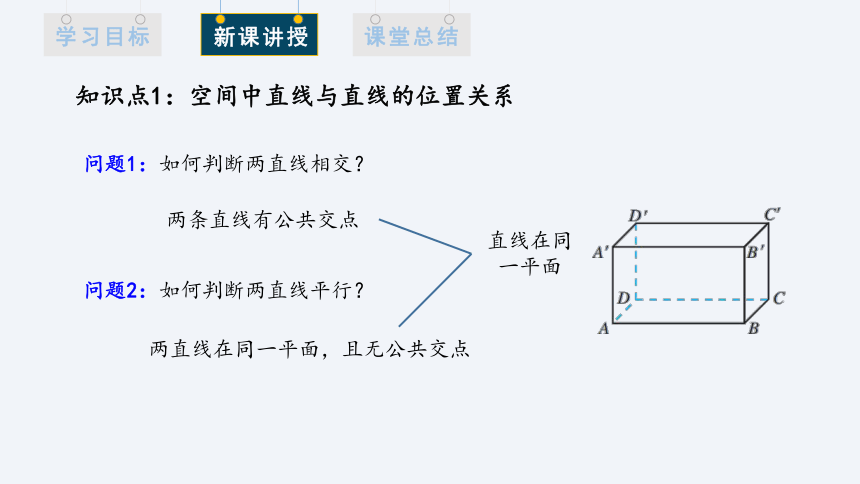
问题1:如何判断两直线相交?
两条直线有公共交点
知识点1:空间中直线与直线的位置关系
问题2:如何判断两直线平行?
两直线在同一平面,且无公共交点
空间内,我们把不同在任何一平面内的两条直线称之为异面直线.
棱AB与A'D', DD', B'C', CC'异面
问题3:在正方体的面ABCD中,AB与AD相交,AB与CD平行.AB和CC'的位置关系是平行还是相交?
空间两条直线的位置关系:
共面直线
异面直线
相交直线
平行直线
不同在任何一个平面内,没有公共点.
同一平面内,有且只有一个公共点
同一平面内,没有公共点;
归纳总结
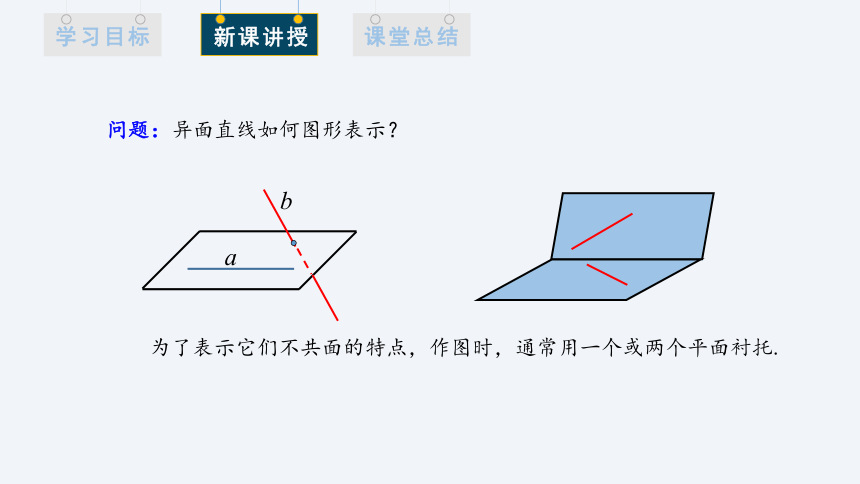
问题:异面直线如何图形表示?
为了表示它们不共面的特点,作图时,通常用一个或两个平面衬托.
a
b
练一练:
1.直线a与直线b相交,直线c与直线b相交,则直线a与直线c的位置关系是( )
A.相交 B.平行
C.异面 D.以上都有可能
D
问题:观察长方体ABCD-A1B1C1D1,直线A1B与长方体的六个面所在平面有几种位置关系
知识点2:空间中直线与平面的位置关系
——直线A1B与平面ABB1A1有无数个公共点
直线在平面内
——直线A1B与平面ADD1A1有一个公共点
——直线A1B与平面CDD1C1没有公共点
直线与平面相交
直线与平面平行
直线在平面外
图形 公共点个数 文字语言(读法) 符号语言
l
α
l
α
直线在平面α内
有无数个
直线与平面α相交
有且只有一个交点
l
α
A
直线与平面α平行
无交点
l∥α
l α
l∩α=A
问题:长方体ABCD-A1B1C1D1的六个面,两两之间的位置关系有几种
知识点3:空间中平面与平面的位置关系
没有公共点
两平面平行
有一条公共直线
两平面相交
位置关系 图形语言 符号语言 公共点个数
两平面平行
两平面相交
0
无数个
(在一条直线上)
问题1:“直线与直线、直线与平面、平面与平面之间没有公共点就行,平行就是没有公共点”这句话对吗?为什么
直线与直线在同一平面内没有公共点才平行,异面直线没有公共点但不在同一平面内.
问题2:“直线与直线、直线与平面、平面与平面”之间有两个公共点时,它们的位置关系如何
直线与直线重合;直线在平面内;平面和平面重合或相交于过着两点的直线
例1:用符号表示下列图形中直线、平面之间的位置关系.
(1)
(2)
解:(1)α∩β=l,a∩α=A,a∩β=B.
(2)α∩β=l,a α,b β,a∩l=P,b∩l=P,a∩b=P.
例2: 直线AB与a具有怎样的位置关系?为什么?
这与A α矛盾,所以直线AB与a是异面直线.
解:直线AB与a是异面直线,
若直线AB与a不是异面直线,则它们相交或平行.
设它们确定的平面为β,则B∈β,a β.
由于经过点B与直线a有且仅有一个平面α,
因此平面α与β重合,从而AB α,进而A∈α ,
与一个平面相交的直线和这个平面内不经过交点的直线是异面直线
要点概括整合
空间点、直线、平面之间的位置关系
直线与直线的位置关系
平面与平面的位置关系
相交
直线在平面外
直线与平面的位置关系
平行
异面
共面
直线在平面内
直线与平面相交
直线与平面平行
相交
平行
8.4.2 空间点、直线、平面之间的位置关系
1.了解空间中两条直线间的位置关系,理解异面直线的定义
2.了解直线与平面之间的三种位置关系,并能判断直线与平面的位置关系,会用符号语言和图形语言表示
3.了解平面与平面之间的两种位置关系,会用符号语言和图形语言表示
在同一平面内,两条直线有几种位置关系?空间中两条直线有没有其他的位置关系?
直线在同一平面
问题1:如何判断两直线相交?
两条直线有公共交点
知识点1:空间中直线与直线的位置关系
问题2:如何判断两直线平行?
两直线在同一平面,且无公共交点
空间内,我们把不同在任何一平面内的两条直线称之为异面直线.
棱AB与A'D', DD', B'C', CC'异面
问题3:在正方体的面ABCD中,AB与AD相交,AB与CD平行.AB和CC'的位置关系是平行还是相交?
空间两条直线的位置关系:
共面直线
异面直线
相交直线
平行直线
不同在任何一个平面内,没有公共点.
同一平面内,有且只有一个公共点
同一平面内,没有公共点;
归纳总结
问题:异面直线如何图形表示?
为了表示它们不共面的特点,作图时,通常用一个或两个平面衬托.
a
b
练一练:
1.直线a与直线b相交,直线c与直线b相交,则直线a与直线c的位置关系是( )
A.相交 B.平行
C.异面 D.以上都有可能
D
问题:观察长方体ABCD-A1B1C1D1,直线A1B与长方体的六个面所在平面有几种位置关系
知识点2:空间中直线与平面的位置关系
——直线A1B与平面ABB1A1有无数个公共点
直线在平面内
——直线A1B与平面ADD1A1有一个公共点
——直线A1B与平面CDD1C1没有公共点
直线与平面相交
直线与平面平行
直线在平面外
图形 公共点个数 文字语言(读法) 符号语言
l
α
l
α
直线在平面α内
有无数个
直线与平面α相交
有且只有一个交点
l
α
A
直线与平面α平行
无交点
l∥α
l α
l∩α=A
问题:长方体ABCD-A1B1C1D1的六个面,两两之间的位置关系有几种
知识点3:空间中平面与平面的位置关系
没有公共点
两平面平行
有一条公共直线
两平面相交
位置关系 图形语言 符号语言 公共点个数
两平面平行
两平面相交
0
无数个
(在一条直线上)
问题1:“直线与直线、直线与平面、平面与平面之间没有公共点就行,平行就是没有公共点”这句话对吗?为什么
直线与直线在同一平面内没有公共点才平行,异面直线没有公共点但不在同一平面内.
问题2:“直线与直线、直线与平面、平面与平面”之间有两个公共点时,它们的位置关系如何
直线与直线重合;直线在平面内;平面和平面重合或相交于过着两点的直线
例1:用符号表示下列图形中直线、平面之间的位置关系.
(1)
(2)
解:(1)α∩β=l,a∩α=A,a∩β=B.
(2)α∩β=l,a α,b β,a∩l=P,b∩l=P,a∩b=P.
例2: 直线AB与a具有怎样的位置关系?为什么?
这与A α矛盾,所以直线AB与a是异面直线.
解:直线AB与a是异面直线,
若直线AB与a不是异面直线,则它们相交或平行.
设它们确定的平面为β,则B∈β,a β.
由于经过点B与直线a有且仅有一个平面α,
因此平面α与β重合,从而AB α,进而A∈α ,
与一个平面相交的直线和这个平面内不经过交点的直线是异面直线
要点概括整合
空间点、直线、平面之间的位置关系
直线与直线的位置关系
平面与平面的位置关系
相交
直线在平面外
直线与平面的位置关系
平行
异面
共面
直线在平面内
直线与平面相交
直线与平面平行
相交
平行
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
