9.1.1 简单随机抽样 第1课时 课件(共18张PPT)
文档属性
| 名称 | 9.1.1 简单随机抽样 第1课时 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-11 18:09:08 | ||
图片预览






文档简介
(共18张PPT)
9.1.1 简单随机抽样
第1课时
1.正确理解总体、个体、样本、普查、抽样调查的概念
2.理解简单随机抽样的概念,掌握抽签法和随机数法的一般步骤
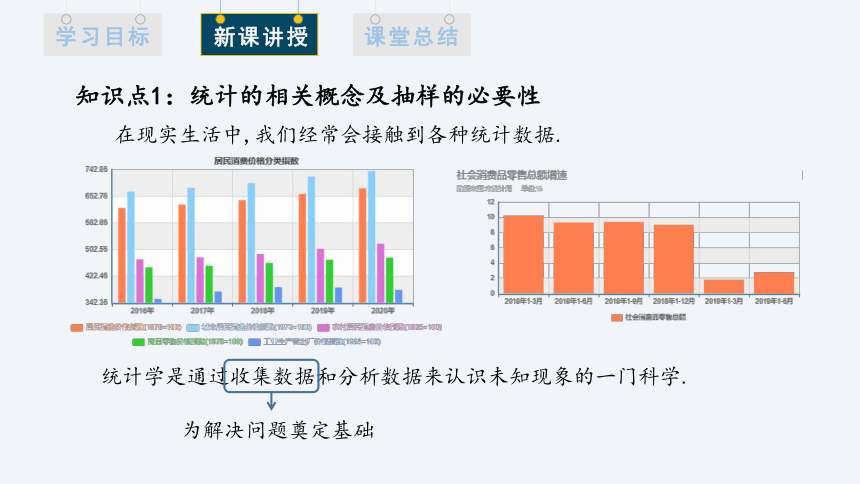
在现实生活中,我们经常会接触到各种统计数据.
为解决问题奠定基础
知识点1:统计的相关概念及抽样的必要性
统计学是通过收集数据和分析数据来认识未知现象的一门科学.
对每一个调查对象都进行调查的方法,称为全面调查,又称普查.
根据一定目的,从总体中抽取一部分个体进行调查,并以此为依据
对总体的情况做出估计和判断的调查方法,称为抽样调查.
把调查对象的全体称为总体,成总体的每一个调查对象称为个体.
从总体中抽取的一部分个体叫做这个总体的一个样本.
样本中包含的个体数称为样本量.
调查样本获得的变量值为样本数据.
思考:下列调查,适合采用的是普查还是抽查 为什么
调查一个班级学生每周的体育运动时间
为了防止新冠状病毒肺炎的蔓延,调查学生每天晨午晚体温
测试一批待收瓶装牛奶细菌数是否超标
“普查”与“抽样”的优劣对比:
方式 优点 缺点
普查
抽样调查
全面、准确性高
花费少,效率高
工作量大,时间长
耗人力、物力、财力
获得的信息不够全面
对象很少时,最好
对象很多,或检验对对象具有破坏性
普查需要花费大量的财力、物力,有时甚至具有破坏性,因而不宜经常进行.故在有些调查中,抽样调查具有不可替代的作用.
思考1:如何科学地抽取样本 怎样使抽取的样本充分地反映总体的情况
知识点2:简单随机抽样
可以通过放回摸球,用频率估计红球的比例
思考2:假设口袋中有红色和白色共1000个小球,除颜色外,小球的大小、质地完全相同.如何通过抽样调查的方法估计袋中红球所占的比例?
总体内的各个个体被抽到的概率都相等
存在不足
通过不放回摸球,用频率估计红球的比例
一般地,设一个总体含有N(N为正整数)个个体,从中逐个抽取n(1≤n如果抽取是不放回的,称为不放回简单随机抽样.
如果抽取是放回的,叫做放回简单随机抽样;
通过简单随机抽样获得的样本称为简单随机样本.
如没特殊说明,本章所称简单随机抽样指不放回简单随机抽样.
效率更高
例1 下面的抽样方法是简单随机抽样吗?为什么?
(1)从无数个个体中抽取20个个体作为样本;
(2)从50台冰箱中一次性抽取5台冰箱进行质量检查;
(3)某班有40名同学,指定个子最高的5名同学参加学校组织的篮球赛;
(4)一彩民选号,从装有36个大小、形状都相同的号签的盒子中无放回地抽出6个号签.
总体的个数不是有限的
×
×
不是逐个抽取
×
不是等可能抽样
√
简单随机抽样的特点
1.有限性:总体中个体数有限;
2.逐一性:从总体中逐一抽取,这样便于在抽样试验中进行操作;
3.等可能性:简单随机抽样是一种等可能抽样,在整个抽样过程中每个个体被抽取到的可能性相等,从而保证了这种抽样方式的公平性.
归纳总结
知识点3:两种常见的简单随机抽样方法
问题:一家家具厂要为树人中学高一年级制作课桌椅,他们事先想了解全体高一年级学生的平均身高,以便设定可调节课桌椅的标准高度.已知树人中学高一年级有712名学生,如果要通过简单随机抽样的方法调查高一年级学生的平均身高,应该怎样抽取样本
抽签法
开始
712名同学从1到712编号
制作编号为1到712的号签(共712个)
将712个号签搅拌均匀
随机从中逐一抽出n个号签
与所抽取号码一致的学生即被选中
结束
归纳总结
抽签法的一般步骤:
(1)确定总体容量N并编号;
(2)制签并放入不透明容器中;
(3)充分搅拌均匀;
(4)不放回地逐个抽取n次,得到容量为n的样本.
随机数法,即利用随机试验,信息技术(计算器、电子表格软件、R统计软件、手机软件等)生成随机数进行抽样.
随机数法
(1)将总体中的N个个体编号;
步骤:
(2)用随机数工具产生1~N范围内的整数随机数,把产生的随机数作为抽中的编号;
(3)重复上述过程,直到抽足样本所需要的人数.
说明:如果生成的随机数有重复,即同一编号多次被抽到,可以剔除重复的编号并重新产生随机数,直到产生不同的编号个数等于样本数.
随机数的产生
1.用随机试验生成随机数
准备10个大小质地一样的小球,小球上分别写上数字0,1,2,…9,放在不透明的盒子中,
当编号是三位的时候,有放回抽取3次,抽前充分搅拌,第一、二、三次号作摸到数字分别作为百、十、个位数.
2.用信息技术生成随机数
①用计算器生成随机数
②用电子表格软件生成随机数
③用R统计软件生成随机数
RandInt# (1,712)
=RANDBETWEEN (1,712)
sample (1:712,50,replace=F)
思考:在简单随机抽样中,样本量是否越大越好?
抽样方法 优点 缺点 适用范围
抽签法
随机数法
两种抽样方法的比较
抽样调查中样本量的选择要根据实际问题的需要,并不一定是越大越好
简单易行
随机数表数字较多,因此当总体容量较多时,抽取较为便利
总体量较大时,操作起来较麻烦
适用于总体量大、样本量较小的情形
适用于总体中个体数不多的情形
总体量较大,样本量也很大时,利用随机数法抽取样本仍然不方便
要点概括整合
简单随机抽样
抽签法
随机数法
调查
全面调查
抽样调查
9.1.1 简单随机抽样
第1课时
1.正确理解总体、个体、样本、普查、抽样调查的概念
2.理解简单随机抽样的概念,掌握抽签法和随机数法的一般步骤
在现实生活中,我们经常会接触到各种统计数据.
为解决问题奠定基础
知识点1:统计的相关概念及抽样的必要性
统计学是通过收集数据和分析数据来认识未知现象的一门科学.
对每一个调查对象都进行调查的方法,称为全面调查,又称普查.
根据一定目的,从总体中抽取一部分个体进行调查,并以此为依据
对总体的情况做出估计和判断的调查方法,称为抽样调查.
把调查对象的全体称为总体,成总体的每一个调查对象称为个体.
从总体中抽取的一部分个体叫做这个总体的一个样本.
样本中包含的个体数称为样本量.
调查样本获得的变量值为样本数据.
思考:下列调查,适合采用的是普查还是抽查 为什么
调查一个班级学生每周的体育运动时间
为了防止新冠状病毒肺炎的蔓延,调查学生每天晨午晚体温
测试一批待收瓶装牛奶细菌数是否超标
“普查”与“抽样”的优劣对比:
方式 优点 缺点
普查
抽样调查
全面、准确性高
花费少,效率高
工作量大,时间长
耗人力、物力、财力
获得的信息不够全面
对象很少时,最好
对象很多,或检验对对象具有破坏性
普查需要花费大量的财力、物力,有时甚至具有破坏性,因而不宜经常进行.故在有些调查中,抽样调查具有不可替代的作用.
思考1:如何科学地抽取样本 怎样使抽取的样本充分地反映总体的情况
知识点2:简单随机抽样
可以通过放回摸球,用频率估计红球的比例
思考2:假设口袋中有红色和白色共1000个小球,除颜色外,小球的大小、质地完全相同.如何通过抽样调查的方法估计袋中红球所占的比例?
总体内的各个个体被抽到的概率都相等
存在不足
通过不放回摸球,用频率估计红球的比例
一般地,设一个总体含有N(N为正整数)个个体,从中逐个抽取n(1≤n
如果抽取是放回的,叫做放回简单随机抽样;
通过简单随机抽样获得的样本称为简单随机样本.
如没特殊说明,本章所称简单随机抽样指不放回简单随机抽样.
效率更高
例1 下面的抽样方法是简单随机抽样吗?为什么?
(1)从无数个个体中抽取20个个体作为样本;
(2)从50台冰箱中一次性抽取5台冰箱进行质量检查;
(3)某班有40名同学,指定个子最高的5名同学参加学校组织的篮球赛;
(4)一彩民选号,从装有36个大小、形状都相同的号签的盒子中无放回地抽出6个号签.
总体的个数不是有限的
×
×
不是逐个抽取
×
不是等可能抽样
√
简单随机抽样的特点
1.有限性:总体中个体数有限;
2.逐一性:从总体中逐一抽取,这样便于在抽样试验中进行操作;
3.等可能性:简单随机抽样是一种等可能抽样,在整个抽样过程中每个个体被抽取到的可能性相等,从而保证了这种抽样方式的公平性.
归纳总结
知识点3:两种常见的简单随机抽样方法
问题:一家家具厂要为树人中学高一年级制作课桌椅,他们事先想了解全体高一年级学生的平均身高,以便设定可调节课桌椅的标准高度.已知树人中学高一年级有712名学生,如果要通过简单随机抽样的方法调查高一年级学生的平均身高,应该怎样抽取样本
抽签法
开始
712名同学从1到712编号
制作编号为1到712的号签(共712个)
将712个号签搅拌均匀
随机从中逐一抽出n个号签
与所抽取号码一致的学生即被选中
结束
归纳总结
抽签法的一般步骤:
(1)确定总体容量N并编号;
(2)制签并放入不透明容器中;
(3)充分搅拌均匀;
(4)不放回地逐个抽取n次,得到容量为n的样本.
随机数法,即利用随机试验,信息技术(计算器、电子表格软件、R统计软件、手机软件等)生成随机数进行抽样.
随机数法
(1)将总体中的N个个体编号;
步骤:
(2)用随机数工具产生1~N范围内的整数随机数,把产生的随机数作为抽中的编号;
(3)重复上述过程,直到抽足样本所需要的人数.
说明:如果生成的随机数有重复,即同一编号多次被抽到,可以剔除重复的编号并重新产生随机数,直到产生不同的编号个数等于样本数.
随机数的产生
1.用随机试验生成随机数
准备10个大小质地一样的小球,小球上分别写上数字0,1,2,…9,放在不透明的盒子中,
当编号是三位的时候,有放回抽取3次,抽前充分搅拌,第一、二、三次号作摸到数字分别作为百、十、个位数.
2.用信息技术生成随机数
①用计算器生成随机数
②用电子表格软件生成随机数
③用R统计软件生成随机数
RandInt# (1,712)
=RANDBETWEEN (1,712)
sample (1:712,50,replace=F)
思考:在简单随机抽样中,样本量是否越大越好?
抽样方法 优点 缺点 适用范围
抽签法
随机数法
两种抽样方法的比较
抽样调查中样本量的选择要根据实际问题的需要,并不一定是越大越好
简单易行
随机数表数字较多,因此当总体容量较多时,抽取较为便利
总体量较大时,操作起来较麻烦
适用于总体量大、样本量较小的情形
适用于总体中个体数不多的情形
总体量较大,样本量也很大时,利用随机数法抽取样本仍然不方便
要点概括整合
简单随机抽样
抽签法
随机数法
调查
全面调查
抽样调查
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
