新人教版八年级18.1勾股定理
文档属性
| 名称 | 新人教版八年级18.1勾股定理 |  | |
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-22 20:34:00 | ||
图片预览


文档简介
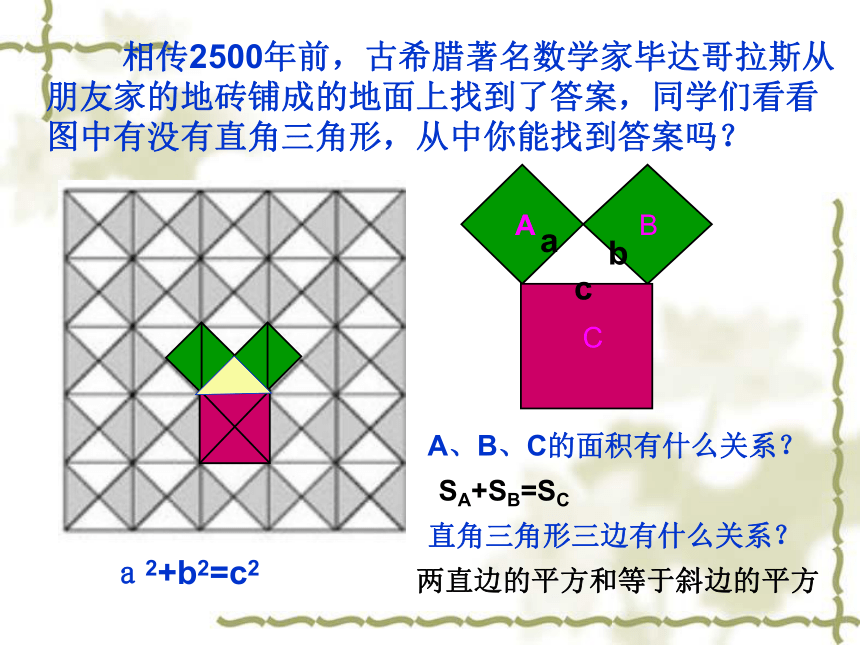
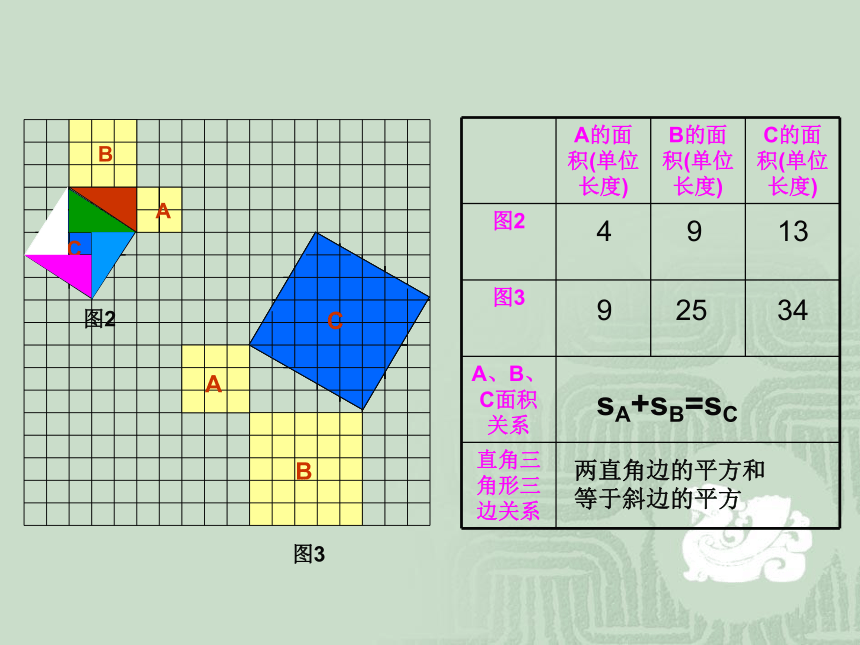
课件26张PPT。热烈欢迎各位领导、老师莅临指导!18.1 勾股定理abc 相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们看看图中有没有直角三角形,从中你能找到答案吗?A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方a2+b2=c2abcABC图2图3491392534sA+sB=sC两直角边的平方和
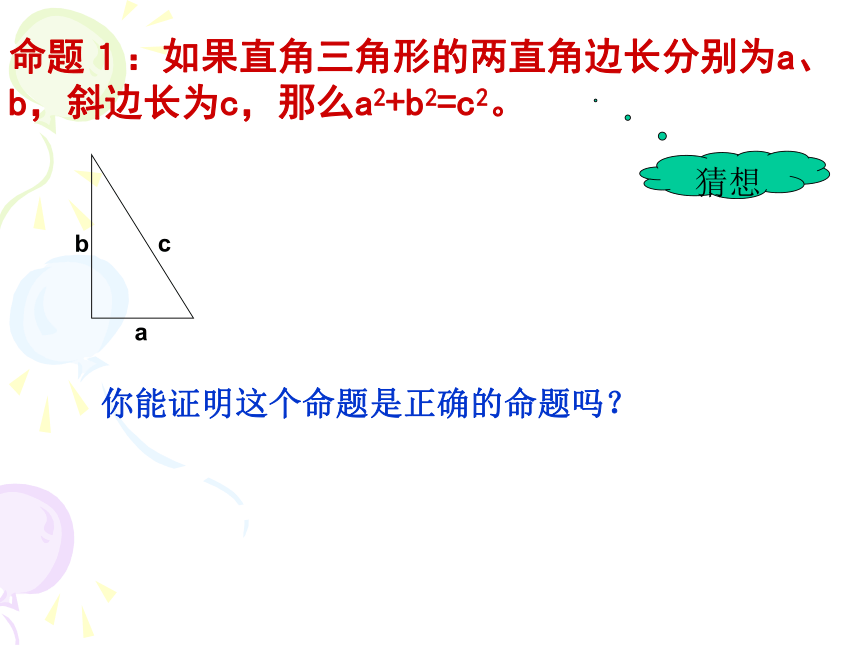
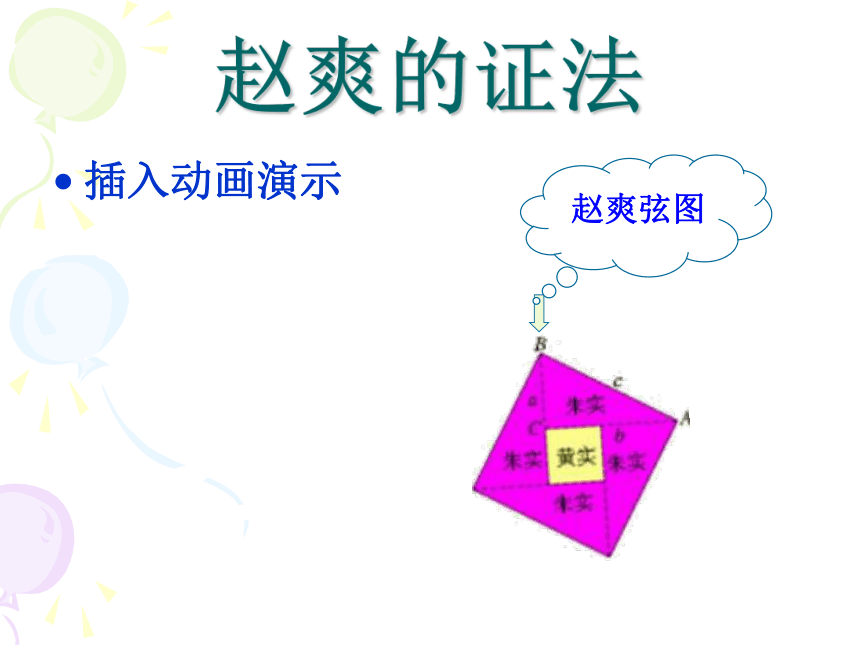
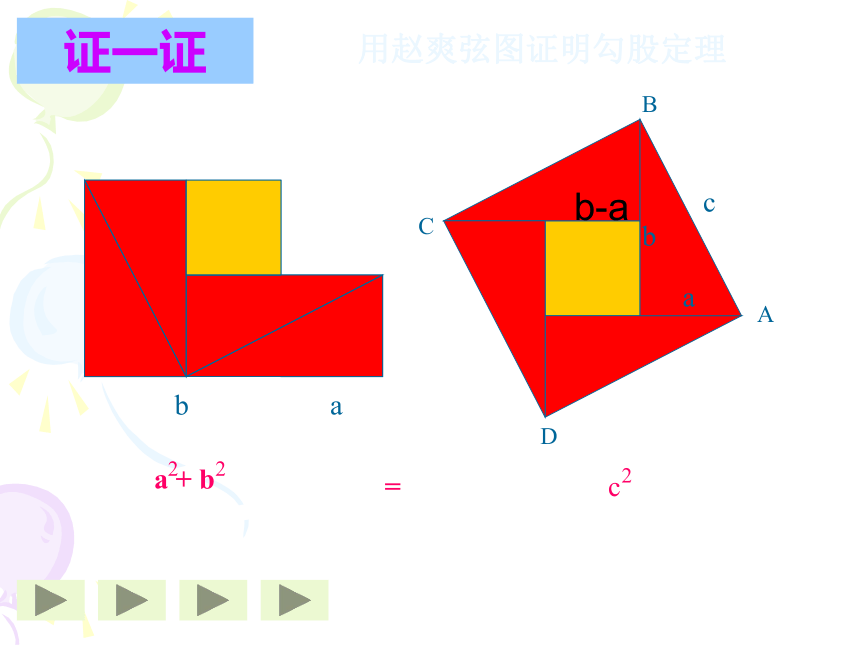
等于斜边的平方命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。abc你能证明这个命题是正确的命题吗?猜想赵爽的证法插入动画演示用赵爽弦图证明勾股定理=证一证b-a在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 定理:经过证明被确认为正确的命题叫做定理。 勾股定理:如果直角三角形的两直角边长分别为a、b,斜边为c,那么a2+b2=c2。结论变形直角三角形中,两直角边的平方和等于斜边的平方;
abcc2=a2 + b2练一练:
求下列图中字母所表示的正方形的面积=625=144 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和S1S2解:∵ SE= 49S1=SA+SBS2=SC+SD∴ SA+SB+SC+SD
= S1+S2 = SE = 49例1、求出下列直角三角形中未知边的长度解:由勾股定理得:x2 =36+64x2 =100x2=62+82∴ x=10∵ x2+52=132∴ x2=132-52x2 =169-25x2 =144∴ x=12∵ x > 0∵ x > 0(1)求出下列直角三角形中未知的边.练 习回答:①在解决上述问题时,每个直角三角形需知道几个条件?②直角三角形哪条边最长?1.在Rt△ABC中,∠C=90°.
(1) 已知:a=40,c=41,求b;
(2) 已知: a:b=3:4, c=15,求a、b.(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结做一做:比一比,看谁做的快 32511464如图,在Rt△ABC中,
∠c = 90°例2:如图,一个10米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为8米.①求梯子的底端B距墙角O多少米?②如果梯子的顶端A沿墙角下滑2米至C,请同学们:猜一猜,底端也将滑动2米吗?想一想,是不是梯子顶端下滑多少米?梯子底端也就滑动多少米? 例3.在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里的水有多深? 思考: 做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。3、学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。谢谢
等于斜边的平方命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。abc你能证明这个命题是正确的命题吗?猜想赵爽的证法插入动画演示用赵爽弦图证明勾股定理=证一证b-a在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 定理:经过证明被确认为正确的命题叫做定理。 勾股定理:如果直角三角形的两直角边长分别为a、b,斜边为c,那么a2+b2=c2。结论变形直角三角形中,两直角边的平方和等于斜边的平方;
abcc2=a2 + b2练一练:
求下列图中字母所表示的正方形的面积=625=144 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和S1S2解:∵ SE= 49S1=SA+SBS2=SC+SD∴ SA+SB+SC+SD
= S1+S2 = SE = 49例1、求出下列直角三角形中未知边的长度解:由勾股定理得:x2 =36+64x2 =100x2=62+82∴ x=10∵ x2+52=132∴ x2=132-52x2 =169-25x2 =144∴ x=12∵ x > 0∵ x > 0(1)求出下列直角三角形中未知的边.练 习回答:①在解决上述问题时,每个直角三角形需知道几个条件?②直角三角形哪条边最长?1.在Rt△ABC中,∠C=90°.
(1) 已知:a=40,c=41,求b;
(2) 已知: a:b=3:4, c=15,求a、b.(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结做一做:比一比,看谁做的快 32511464如图,在Rt△ABC中,
∠c = 90°例2:如图,一个10米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为8米.①求梯子的底端B距墙角O多少米?②如果梯子的顶端A沿墙角下滑2米至C,请同学们:猜一猜,底端也将滑动2米吗?想一想,是不是梯子顶端下滑多少米?梯子底端也就滑动多少米? 例3.在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里的水有多深? 思考: 做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。3、学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。谢谢
