2024年中考数学一轮复习练习题:锐角三角函数(含答案)
文档属性
| 名称 | 2024年中考数学一轮复习练习题:锐角三角函数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 250.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 18:02:40 | ||
图片预览



文档简介
2024年中考数学一轮复习练习题:锐角三角函数
一、选择题
1.在中,,则( )
A.1 B.2 C. D.
2.的值等于( )
A.1 B. C. D.2
3.学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳到地面,如图所示.已彩旗绳与地面形成角(即)、彩旗绳固定在地面的位置与图书馆相距32米(即米),则彩旗绳的长度为( )
A.米 B.米 C.米 D.米
4.如图所示,有一天桥高为5米,是通向天桥的斜坡,,市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使,则的长度约为(参考数据:)( )
A.米 B.米 C.米 D.米
5.如图,某货船以24海里/时的速度从处向正东方向的处航行,在点处测得某岛在北偏东的方向.该货船航行30分钟后到达处,此时测得该岛在北偏东的方向上.则货船在航行中离小岛的最短距离是( )
A.12海里 B.海里 C.海里 D.海里
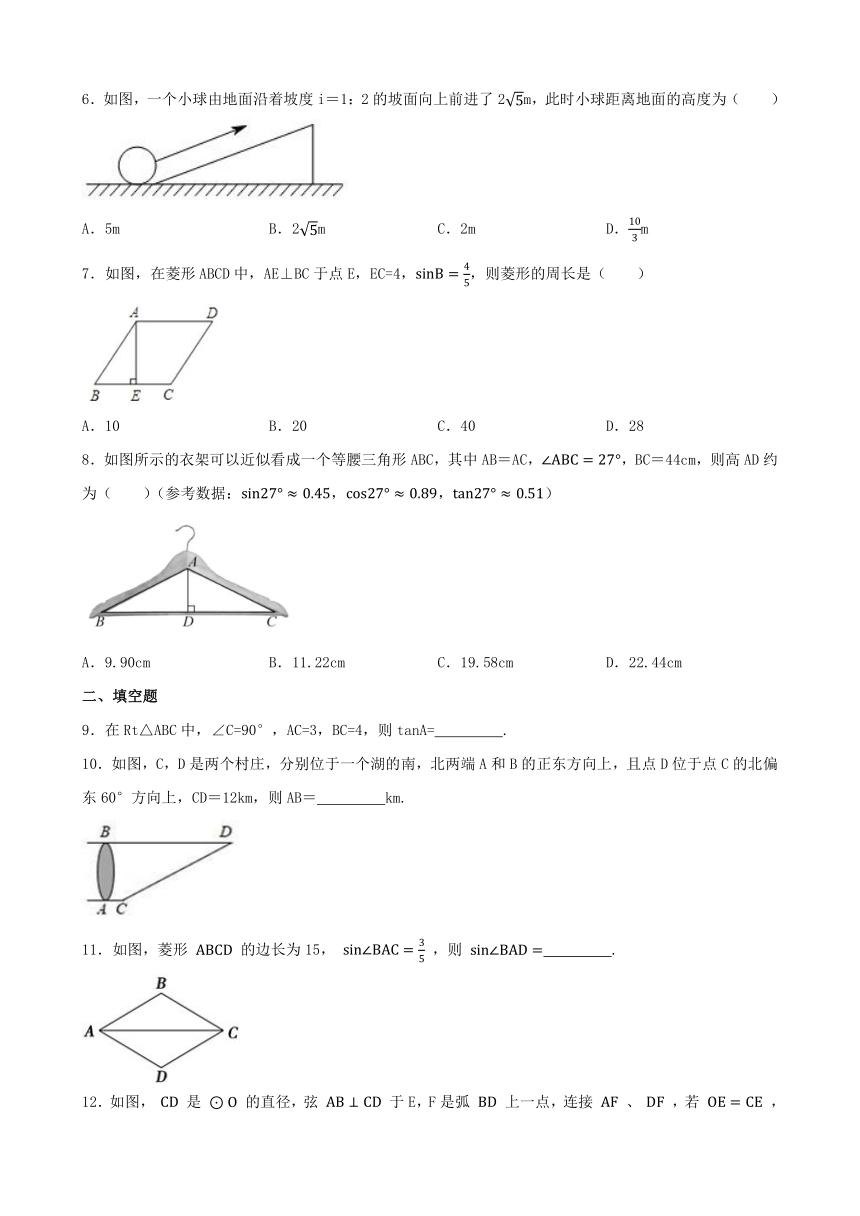
6.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了2m,此时小球距离地面的高度为( )
A.5m B.2m C.2m D.m
7.如图,在菱形ABCD中,AE⊥BC于点E,EC=4,,则菱形的周长是( )
A.10 B.20 C.40 D.28
8.如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,,BC=44cm,则高AD约为( )(参考数据:,,)
A.9.90cm B.11.22cm C.19.58cm D.22.44cm
二、填空题
9.在Rt△ABC中,∠C=90°,AC=3,BC=4,则tanA= .
10.如图,C,D是两个村庄,分别位于一个湖的南,北两端A和B的正东方向上,且点D位于点C的北偏东60°方向上,CD=12km,则AB= km.
11.如图,菱形 的边长为15, ,则 .
12.如图, 是 的直径,弦 于E,F是弧 上一点,连接 、 ,若 ,则 的值为 .
13.如图,在 中, ,点 在 边上, ,点E在 边上, ,点F为 上一点, ,若 , ,则 的长为 .
三、解答题
14. 计算:.
15.如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
16.随着近几年我国私家车日愈增多,超速行驶成为引发交通事故的主要原因之一,某中学数学活动小组为开展”文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO =30°,∠PBO=60°.
(1)求A、B之间的路程(保留根号) ;
(2)已知本路段对校车限速为12米/秒,若测得某校车从A到B用了2秒,这辆校车是否超速?请说明理由.
17.如图,已知是的直径,直线是的切线,切点为,,垂足为.连接.
(1)求证:平分;
(2)若,,求的半径.
18.如图,在边长为9的正方形中,等腰的直角顶点与正方形的顶点C重合,斜边EF与正方形的对角线交于点E,射线与交于点P,与交于点Q且.
(1)求证:;
(2)求的长;
(3)求的值.
参考答案
1.A
2.B
3.D
4.D
5.B
6.C
7.C
8.B
9.
10.6
11.
12.
13.4
14.解:
.
15.解:作BE⊥l于点E,DF⊥l于点F.
根据题意,得BE=24mm,DF=48mm.
在Rt△ABE中,sin ,
∴ mm
在Rt△ADF中,cos ,
∴ mm.
∴矩形ABCD的周长=2(40+60)=200mm.
16.(1)解:在,PO=21,∠PAO=30°
∴
在,PO=21,∠PBO=60°
∴
∴
(2)解:超速,理由如下
∵某校车从A到B用了2秒
∴速度为:(米/秒)
∵
∴这辆校车在AB路段超速
17.(1)证明:连接,
∵直线是的切线,
∴,
∵,
∴,
∴,
∵,
∴,
∴,即平分;
(2)解:连接,过点O作于F,则,
∵,,
∴,
∴,
∴,
∴,
∴,
即的半径为
18.(1)证明:四边形是正方形,是等腰直角三角形
,
,
在与中,
∵,
;
(2)解:,
,
,
,
,
,
,
;
(3)解:过点F作于R,
∵,
∴,
∴是等腰直角三角形,
,
在中,
,
,
,
,
,
.
一、选择题
1.在中,,则( )
A.1 B.2 C. D.
2.的值等于( )
A.1 B. C. D.2
3.学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳到地面,如图所示.已彩旗绳与地面形成角(即)、彩旗绳固定在地面的位置与图书馆相距32米(即米),则彩旗绳的长度为( )
A.米 B.米 C.米 D.米
4.如图所示,有一天桥高为5米,是通向天桥的斜坡,,市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使,则的长度约为(参考数据:)( )
A.米 B.米 C.米 D.米
5.如图,某货船以24海里/时的速度从处向正东方向的处航行,在点处测得某岛在北偏东的方向.该货船航行30分钟后到达处,此时测得该岛在北偏东的方向上.则货船在航行中离小岛的最短距离是( )
A.12海里 B.海里 C.海里 D.海里
6.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了2m,此时小球距离地面的高度为( )
A.5m B.2m C.2m D.m
7.如图,在菱形ABCD中,AE⊥BC于点E,EC=4,,则菱形的周长是( )
A.10 B.20 C.40 D.28
8.如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,,BC=44cm,则高AD约为( )(参考数据:,,)
A.9.90cm B.11.22cm C.19.58cm D.22.44cm
二、填空题
9.在Rt△ABC中,∠C=90°,AC=3,BC=4,则tanA= .
10.如图,C,D是两个村庄,分别位于一个湖的南,北两端A和B的正东方向上,且点D位于点C的北偏东60°方向上,CD=12km,则AB= km.
11.如图,菱形 的边长为15, ,则 .
12.如图, 是 的直径,弦 于E,F是弧 上一点,连接 、 ,若 ,则 的值为 .
13.如图,在 中, ,点 在 边上, ,点E在 边上, ,点F为 上一点, ,若 , ,则 的长为 .
三、解答题
14. 计算:.
15.如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
16.随着近几年我国私家车日愈增多,超速行驶成为引发交通事故的主要原因之一,某中学数学活动小组为开展”文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO =30°,∠PBO=60°.
(1)求A、B之间的路程(保留根号) ;
(2)已知本路段对校车限速为12米/秒,若测得某校车从A到B用了2秒,这辆校车是否超速?请说明理由.
17.如图,已知是的直径,直线是的切线,切点为,,垂足为.连接.
(1)求证:平分;
(2)若,,求的半径.
18.如图,在边长为9的正方形中,等腰的直角顶点与正方形的顶点C重合,斜边EF与正方形的对角线交于点E,射线与交于点P,与交于点Q且.
(1)求证:;
(2)求的长;
(3)求的值.
参考答案
1.A
2.B
3.D
4.D
5.B
6.C
7.C
8.B
9.
10.6
11.
12.
13.4
14.解:
.
15.解:作BE⊥l于点E,DF⊥l于点F.
根据题意,得BE=24mm,DF=48mm.
在Rt△ABE中,sin ,
∴ mm
在Rt△ADF中,cos ,
∴ mm.
∴矩形ABCD的周长=2(40+60)=200mm.
16.(1)解:在,PO=21,∠PAO=30°
∴
在,PO=21,∠PBO=60°
∴
∴
(2)解:超速,理由如下
∵某校车从A到B用了2秒
∴速度为:(米/秒)
∵
∴这辆校车在AB路段超速
17.(1)证明:连接,
∵直线是的切线,
∴,
∵,
∴,
∴,
∵,
∴,
∴,即平分;
(2)解:连接,过点O作于F,则,
∵,,
∴,
∴,
∴,
∴,
∴,
即的半径为
18.(1)证明:四边形是正方形,是等腰直角三角形
,
,
在与中,
∵,
;
(2)解:,
,
,
,
,
,
,
;
(3)解:过点F作于R,
∵,
∴,
∴是等腰直角三角形,
,
在中,
,
,
,
,
,
.
同课章节目录
