2024年中考数学一轮复习练习题:反比例函数(含答案)
文档属性
| 名称 | 2024年中考数学一轮复习练习题:反比例函数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 316.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 18:04:06 | ||
图片预览



文档简介
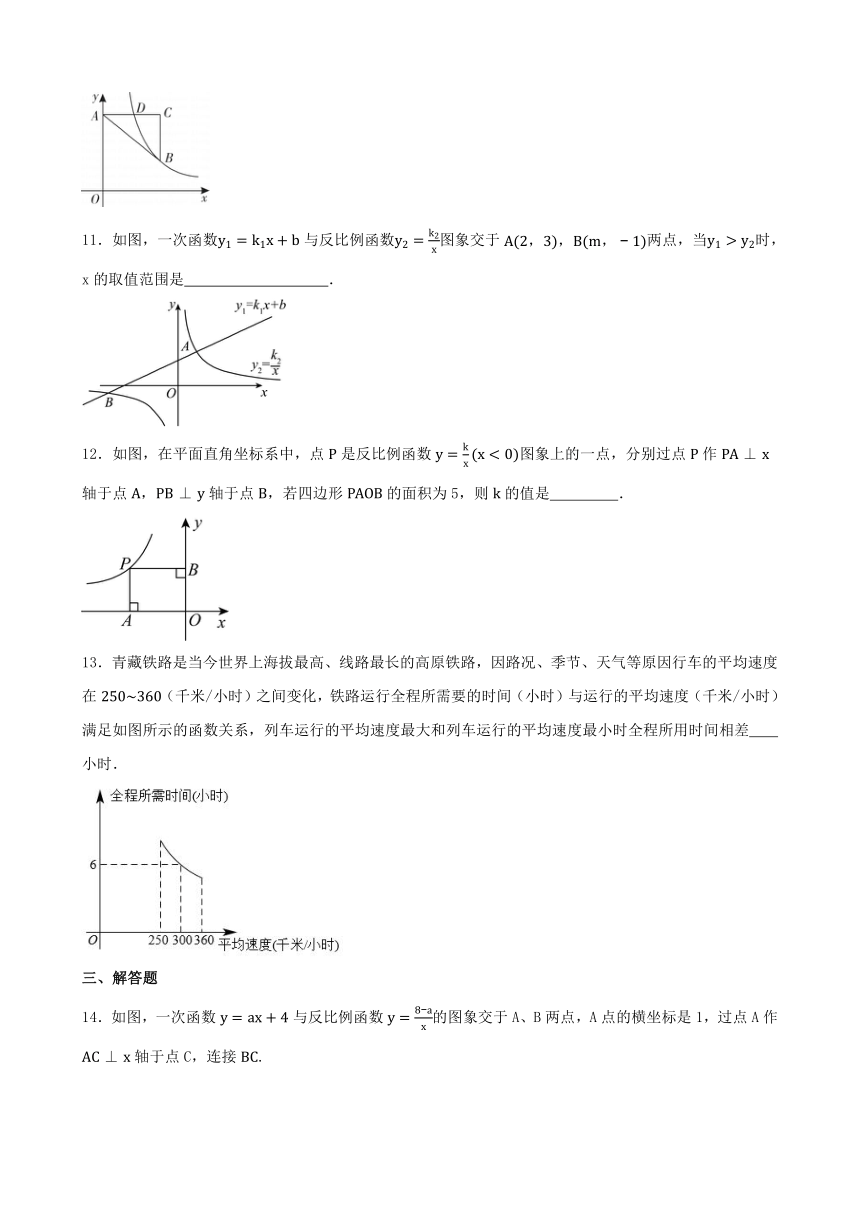
2024年中考数学一轮复习练习题:反比例函数
一、选择题
1.若反比例函数的图象经过点,则k的值是( )
A. B. C. D.
2.反比例函数经过点,则下列说法错误的是( )
A.函数图象经过点 B.函数图象分布在第一、三象限
C.当时,y随x的增大而增大 D.当时,y随x的增大而减小
3.在同一平面直角坐标系中,反比例函数与一次函数(为常数,且)的图象可能是( )
A.B.C.D.
4.若点在反比例函数的图像上,则的大小关系是( )
A. B. C. D.
5.如图,点A在函数的图象上,点B在函数的图象上,且轴,轴于点C,则四边形的面积为( )
A.1 B.2 C.3 D.4
6.某闭合并联电路中,各支路电流与电阻成反比例,如图表示该电路I与电阻R的函数关系图象,若该电路中某导体电阻为,则导体内通过的电流为( )
A. B. C. D.
7.如图,直线与x轴相交于点A,与函数的图象交于点B,C,点B的横坐标是8,点C的横坐标是,则不等式组的解集是( )
A. B. C. D.
8.如图,A、B是第二象限内双曲线y= 上的点,A、B两点的横坐标分别是a,3a,线段AB的延长线交x轴于点C,S△AOC=12.则k的值为( )
A.﹣6 B.﹣5 C.﹣4 D.﹣3
二、填空题
9.如图,的顶点A在反比例函数的图象上,点B在y轴上,点C,点D在轴上,AD与y轴交于点E,若,则的值为 .
10. 如图,在中,,,,的顶点在轴的正半轴上,点,点在第一象限,且直角边平行于轴,反比例函数且的图象经过点和边的中点,则的值为 .
11.如图,一次函数与反比例函数图象交于两点,当时,x的取值范围是 .
12.如图,在平面直角坐标系中,点是反比例函数图象上的一点,分别过点作轴于点,轴于点,若四边形的面积为5,则的值是 .
13.青藏铁路是当今世界上海拔最高、线路最长的高原铁路,因路况、季节、天气等原因行车的平均速度在(千米/小时)之间变化,铁路运行全程所需要的时间(小时)与运行的平均速度(千米/小时)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差 小时.
三、解答题
14.如图,一次函数与反比例函数的图象交于A、B两点,A点的横坐标是1,过点A作轴于点C,连接.
(1)求一次函数与反比例函数的解析式;
(2)求点B的坐标,直接写出不等式的解集.
15.经研究发现,近视眼镜的度数y(度)与镜片焦距x(m)之间的关系满足反比例函数,已知小明的近视眼镜度数为200度,他的镜片焦距为0.5m.
(1)求y与x之间的函数关系式;
(2)已知王力的近视眼镜度数为400度,请你求出王力近视眼镜的镜片焦距.
16.如图,在平面直角坐标系xOy中,已知正比例函数y1=﹣2x的图象与反比例函数y2= 的图象交于A(﹣1,n),B两点.
(1)求出反比例函数的解析式及点B的坐标;
(2)观察图象,请直接写出满足y≤2的取值范围;
(3)点P是第四象限内反比例函数的图象上一点,若△POB的面积为1,请直接写出点P的横坐标.
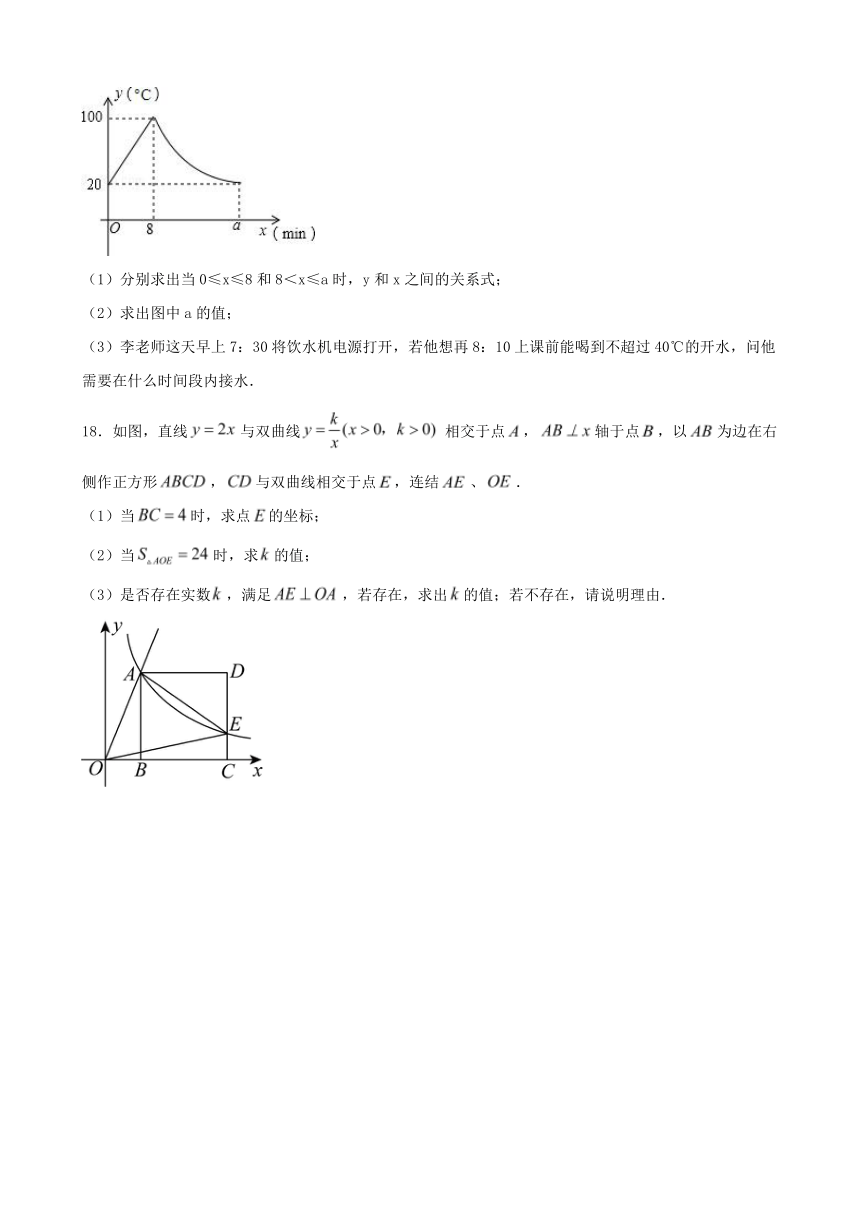
17.某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想再8:10上课前能喝到不超过40℃的开水,问他需要在什么时间段内接水.
18.如图,直线与双曲线相交于点,轴于点,以为边在右侧作正方形,与双曲线相交于点,连结、.
(1)当时,求点的坐标;
(2)当时,求的值;
(3)是否存在实数,满足,若存在,求出的值;若不存在,请说明理由.
参考答案
1.D
2.C
3.B
4.B
5.B
6.B
7.B
8.A
9.10
10.12
11.-6<x<0或x>2
12.
13.2.2
14.(1)解:联立得,
∵一次函数与反比例函数的图象交于A、B两点,A点的横坐标是1,
∴是方程的一个解,
∴,
∴,
∴一次函数解析式为,反比例函数解析式为;
(2)解:联立得,
∴,
解得或,
当时,,
∴点B的坐标为,
∵当或时,反比例函数图象在一次函数图象上方,
∴不等式的解集为或.
15.(1)解:根据题意,得
点(0.5,200)满足反比例函数,
∴,解得k=100,
∴y与x之间的函数关系式为.
(2)解:当y=400时,,解得x=0.25,
∴王力近视眼镜的镜片焦距为0.25m.
16.(1)解:把A(﹣1,n)代入y=﹣2x,可得n=2,
∴A(﹣1,2),
把A(﹣1,2)代入y= ,可得k=﹣2,
∴反比例函数的表达式为y=﹣ ,
∵点B与点A关于原点对称,
∴B(1,﹣2).
(2)解:∵A(﹣1,2),
∴y≤2的取值范围是x<﹣1或x>0;
(3)解:作BM⊥x轴于M,PN⊥x轴于N,
∵S梯形MBPN=S△POB=1,
设P(m,﹣ ),则 (2+ )(m﹣1)=1或 (2+ )(1﹣m)=1
整理得,m2﹣m﹣1=0或m2+m+1=0,
解得m= .或m= .,
∴P点的横坐标为 .
17.(1)解:当0≤x≤8时,设y=k1x+b,
将(0,20),(8,100)代入y=k1x+b,
得k1=10,b=20,
∴当0≤x≤8时,y=10x+20;
当8<x≤a时,设y= ,
将(8,100)代入,得k2=800,
∴当8<x≤a时,y= ;
故当0≤x≤8时,y=10x+20;当8<x≤a时,y=
(2)解:将y=20代入y= ,
解得a=40
(3)解:8:10﹣8分钟=8:02,
∵10x+20≤40,
∴0<x≤2,
∵ ≤40,
∴20≤x<40.
∴李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前能喝到不超过40℃的热水,
则需要在7:50~8:10时间段内接水
18.(1)解:∵四边形为正方形,,
∴A点的纵坐标为4,
∵A在直线上,
∴,
∴,
∴,
∴,
∴,
∴,
∴反比例函数解析式为,
∵,
∴,
∴,
∴点的坐标为
(2)解:设,
∴,,,
∴,,
∴,
∴,
∴
∵,,
∴,
∴,解得,
∴;
(3)解:不存在.理由如下:
∵四边形是正方形,
∴,,
要使,则,
∵,
∴,
∴,
∴,
由(2)可知,,则点,
∴,,
∴,得,
∴,
∵,
∴不符合题意,不存在
一、选择题
1.若反比例函数的图象经过点,则k的值是( )
A. B. C. D.
2.反比例函数经过点,则下列说法错误的是( )
A.函数图象经过点 B.函数图象分布在第一、三象限
C.当时,y随x的增大而增大 D.当时,y随x的增大而减小
3.在同一平面直角坐标系中,反比例函数与一次函数(为常数,且)的图象可能是( )
A.B.C.D.
4.若点在反比例函数的图像上,则的大小关系是( )
A. B. C. D.
5.如图,点A在函数的图象上,点B在函数的图象上,且轴,轴于点C,则四边形的面积为( )
A.1 B.2 C.3 D.4
6.某闭合并联电路中,各支路电流与电阻成反比例,如图表示该电路I与电阻R的函数关系图象,若该电路中某导体电阻为,则导体内通过的电流为( )
A. B. C. D.
7.如图,直线与x轴相交于点A,与函数的图象交于点B,C,点B的横坐标是8,点C的横坐标是,则不等式组的解集是( )
A. B. C. D.
8.如图,A、B是第二象限内双曲线y= 上的点,A、B两点的横坐标分别是a,3a,线段AB的延长线交x轴于点C,S△AOC=12.则k的值为( )
A.﹣6 B.﹣5 C.﹣4 D.﹣3
二、填空题
9.如图,的顶点A在反比例函数的图象上,点B在y轴上,点C,点D在轴上,AD与y轴交于点E,若,则的值为 .
10. 如图,在中,,,,的顶点在轴的正半轴上,点,点在第一象限,且直角边平行于轴,反比例函数且的图象经过点和边的中点,则的值为 .
11.如图,一次函数与反比例函数图象交于两点,当时,x的取值范围是 .
12.如图,在平面直角坐标系中,点是反比例函数图象上的一点,分别过点作轴于点,轴于点,若四边形的面积为5,则的值是 .
13.青藏铁路是当今世界上海拔最高、线路最长的高原铁路,因路况、季节、天气等原因行车的平均速度在(千米/小时)之间变化,铁路运行全程所需要的时间(小时)与运行的平均速度(千米/小时)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差 小时.
三、解答题
14.如图,一次函数与反比例函数的图象交于A、B两点,A点的横坐标是1,过点A作轴于点C,连接.
(1)求一次函数与反比例函数的解析式;
(2)求点B的坐标,直接写出不等式的解集.
15.经研究发现,近视眼镜的度数y(度)与镜片焦距x(m)之间的关系满足反比例函数,已知小明的近视眼镜度数为200度,他的镜片焦距为0.5m.
(1)求y与x之间的函数关系式;
(2)已知王力的近视眼镜度数为400度,请你求出王力近视眼镜的镜片焦距.
16.如图,在平面直角坐标系xOy中,已知正比例函数y1=﹣2x的图象与反比例函数y2= 的图象交于A(﹣1,n),B两点.
(1)求出反比例函数的解析式及点B的坐标;
(2)观察图象,请直接写出满足y≤2的取值范围;
(3)点P是第四象限内反比例函数的图象上一点,若△POB的面积为1,请直接写出点P的横坐标.
17.某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想再8:10上课前能喝到不超过40℃的开水,问他需要在什么时间段内接水.
18.如图,直线与双曲线相交于点,轴于点,以为边在右侧作正方形,与双曲线相交于点,连结、.
(1)当时,求点的坐标;
(2)当时,求的值;
(3)是否存在实数,满足,若存在,求出的值;若不存在,请说明理由.
参考答案
1.D
2.C
3.B
4.B
5.B
6.B
7.B
8.A
9.10
10.12
11.-6<x<0或x>2
12.
13.2.2
14.(1)解:联立得,
∵一次函数与反比例函数的图象交于A、B两点,A点的横坐标是1,
∴是方程的一个解,
∴,
∴,
∴一次函数解析式为,反比例函数解析式为;
(2)解:联立得,
∴,
解得或,
当时,,
∴点B的坐标为,
∵当或时,反比例函数图象在一次函数图象上方,
∴不等式的解集为或.
15.(1)解:根据题意,得
点(0.5,200)满足反比例函数,
∴,解得k=100,
∴y与x之间的函数关系式为.
(2)解:当y=400时,,解得x=0.25,
∴王力近视眼镜的镜片焦距为0.25m.
16.(1)解:把A(﹣1,n)代入y=﹣2x,可得n=2,
∴A(﹣1,2),
把A(﹣1,2)代入y= ,可得k=﹣2,
∴反比例函数的表达式为y=﹣ ,
∵点B与点A关于原点对称,
∴B(1,﹣2).
(2)解:∵A(﹣1,2),
∴y≤2的取值范围是x<﹣1或x>0;
(3)解:作BM⊥x轴于M,PN⊥x轴于N,
∵S梯形MBPN=S△POB=1,
设P(m,﹣ ),则 (2+ )(m﹣1)=1或 (2+ )(1﹣m)=1
整理得,m2﹣m﹣1=0或m2+m+1=0,
解得m= .或m= .,
∴P点的横坐标为 .
17.(1)解:当0≤x≤8时,设y=k1x+b,
将(0,20),(8,100)代入y=k1x+b,
得k1=10,b=20,
∴当0≤x≤8时,y=10x+20;
当8<x≤a时,设y= ,
将(8,100)代入,得k2=800,
∴当8<x≤a时,y= ;
故当0≤x≤8时,y=10x+20;当8<x≤a时,y=
(2)解:将y=20代入y= ,
解得a=40
(3)解:8:10﹣8分钟=8:02,
∵10x+20≤40,
∴0<x≤2,
∵ ≤40,
∴20≤x<40.
∴李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前能喝到不超过40℃的热水,
则需要在7:50~8:10时间段内接水
18.(1)解:∵四边形为正方形,,
∴A点的纵坐标为4,
∵A在直线上,
∴,
∴,
∴,
∴,
∴,
∴,
∴反比例函数解析式为,
∵,
∴,
∴,
∴点的坐标为
(2)解:设,
∴,,,
∴,,
∴,
∴,
∴
∵,,
∴,
∴,解得,
∴;
(3)解:不存在.理由如下:
∵四边形是正方形,
∴,,
要使,则,
∵,
∴,
∴,
∴,
由(2)可知,,则点,
∴,,
∴,得,
∴,
∵,
∴不符合题意,不存在
同课章节目录
