2024年中考数学二轮复习高频压轴题训练——二次函数与最值(含答案)
文档属性
| 名称 | 2024年中考数学二轮复习高频压轴题训练——二次函数与最值(含答案) | 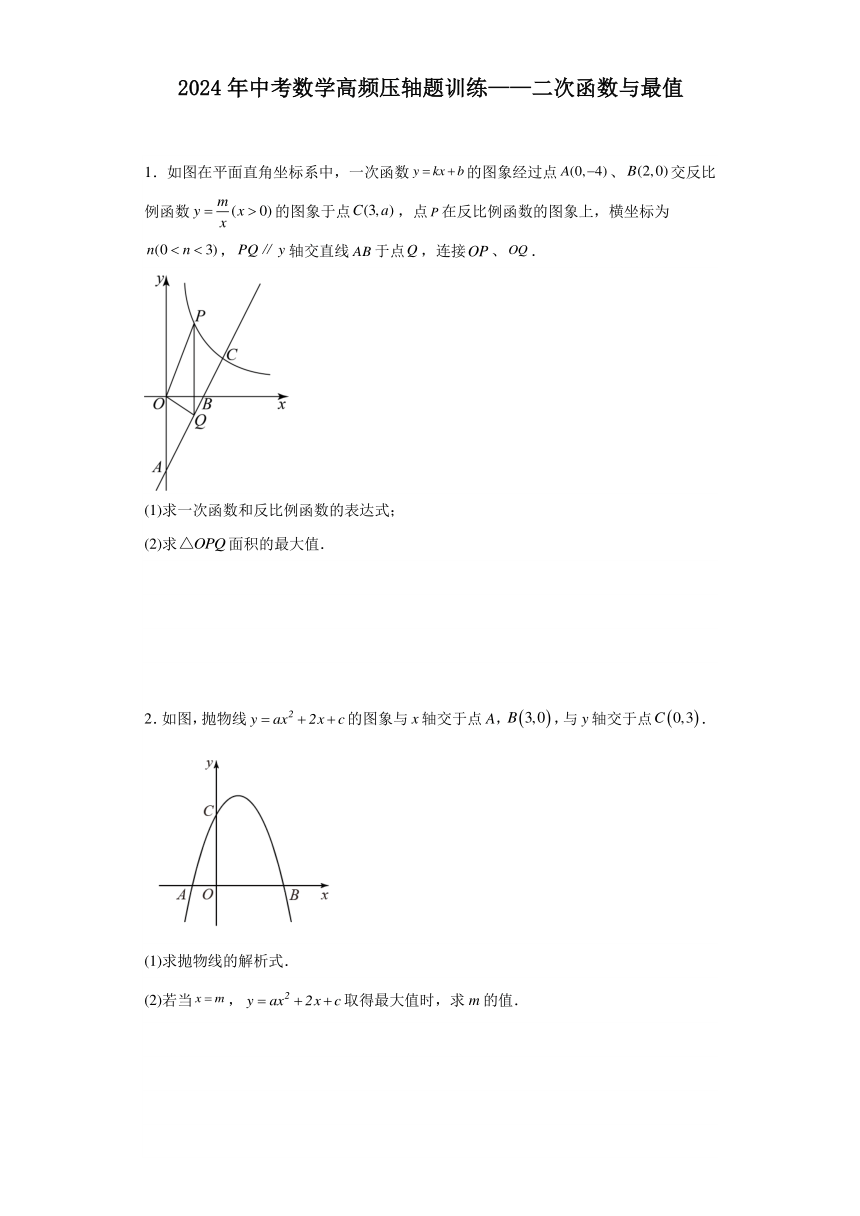 | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 18:04:48 | ||
图片预览




文档简介
2024年中考数学高频压轴题训练——二次函数与最值
1.如图在平面直角坐标系中,一次函数的图象经过点、交反比例函数的图象于点,点在反比例函数的图象上,横坐标为,轴交直线于点,连接、.
(1)求一次函数和反比例函数的表达式;
(2)求面积的最大值.
2.如图,抛物线的图象与x轴交于点A,,与y轴交于点.
(1)求抛物线的解析式.
(2)若当,取得最大值时,求m的值.
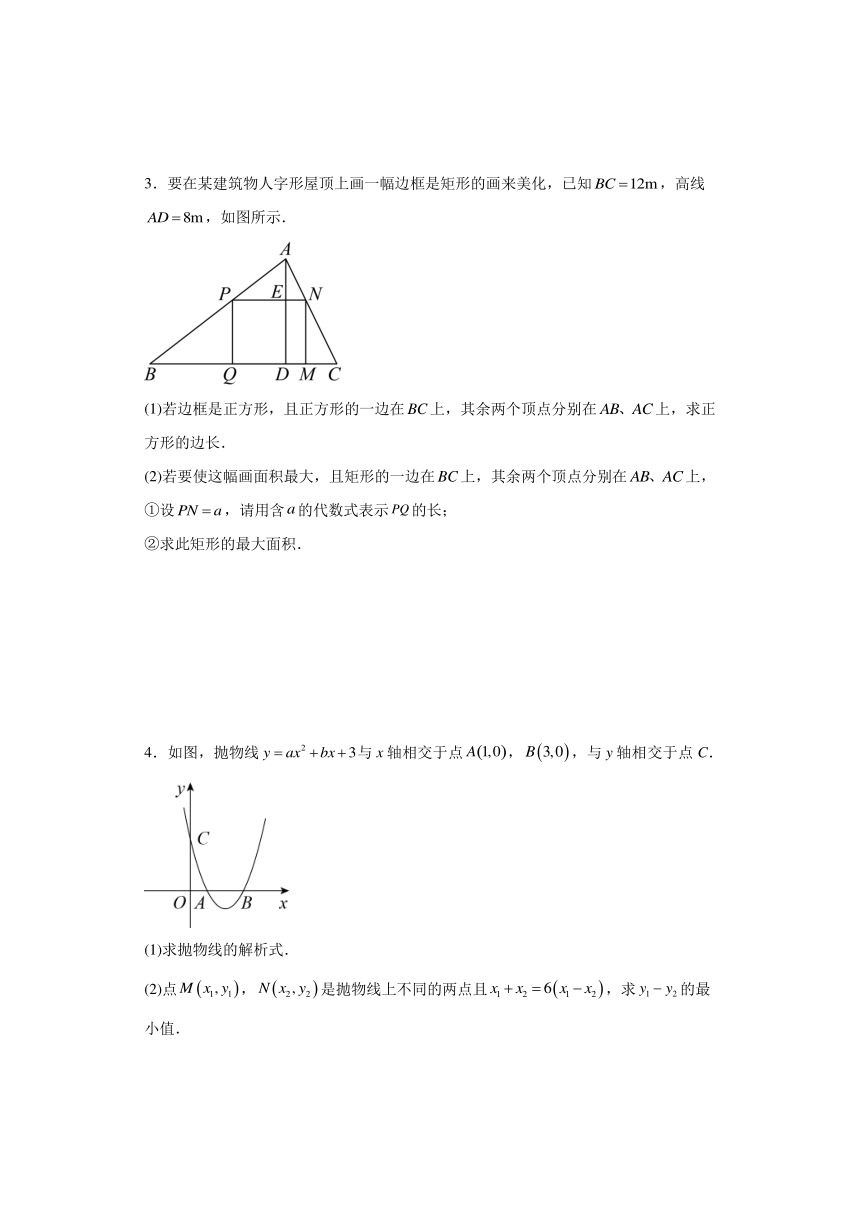
3.要在某建筑物人字形屋顶上画一幅边框是矩形的画来美化,已知,高线,如图所示.
(1)若边框是正方形,且正方形的一边在上,其余两个顶点分别在上,求正方形的边长.
(2)若要使这幅画面积最大,且矩形的一边在上,其余两个顶点分别在上,
①设,请用含的代数式表示的长;
②求此矩形的最大面积.
4.如图,抛物线与x轴相交于点,,与y轴相交于点C.
(1)求抛物线的解析式.
(2)点,是抛物线上不同的两点且,求的最小值.
5.为了改善小区环境,某小区决定在一块一边靠墙(墙长)的空地上修建一个矩形小花园,小花园一边靠墙,另三边用总长的栅栏围住,如下图所示.若设矩形小花园边的长为,面积为.
(1)求y与x之间的函数关系式;
(2)当x为何值时,小花园的面积最大?最大面积是多少?
6.中国茶文化是中国传统文化的重要组成部分之一,代表了中国文化的精髓和卓越,具有丰富的文化内涵和深远的历史意义.某茶庄经销一种绿茶,每千克成本为50元,经市场调查发现:在一段时间内,销售量W(千克)随销售单价x(元/千克)的变化而变化,具体关系式为.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x之间的函数关系式;
(2)当绿茶的销售单价是多少时,该茶庄这种绿茶在这段时间内的销售利润最大 最大利润是多少
7.如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于、点和点,一次函数的图象与抛物线交于两点.
(1)一次函数与二次函数的解析式;
(2)点是线段上的一点,过点作轴的平行线交抛物线于点,求线段的最大值.
8.如图,抛物线与轴交于点,与轴交于点和.若点是所在直线下方该抛物线上的一个动点,过点作平行于轴,交于点.
(1)求三个点,,的坐标;
(2)当点运动至抛物线的顶点时,求此时的长;
(3)设点的横坐标为,的长度为;求与之间的函数关系式,并写出的取值范围;是否存在最值,如有写出最值.
9.如图,抛物线与轴交于,两点(点在点的左侧),与轴交于点,.
(1)求抛物线的解析式;
(2)点为第四象限抛物线上一点,当值最大时,求点的坐标;
10.如图,在足够大的空地上有一段长为40米的旧墙,某人利用旧墙和木栏围成一个矩形菜园,其中,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.设矩形中,边为米,面积为平方米.
(1)求与之间的函数关系式,并写出自变量的取值范围;
(2)求矩形菜园面积的最大值.
11.发射装置距离地面15米的点处,向上发射物体,物体离地面的高度(米)与物体运动的时间(秒)之间满足函数关系,其图象如图所示,物体从发射到落地的运动时间为3秒.
(1)求此函数的解析式;
(2)求发射的物体到达最高点时距地面的高度.
12.如图,二次函数的图象交x轴于点A,B,交y轴于点C,点B的坐标为,对称轴是直线,点P是x轴上一动点,轴,交直线于点M,交抛物线于点N.
(1)求这个二次函数的解析式.
(2)若点P在线段上运动(点P与点A、点O不重合),求四边形面积的最大值,并求出此时点P的坐标.
13.如图,在平面直角坐标系中,抛物线与轴分别交于点和点,与轴交于点.
(1)求抛物线的解析式;
(2)如图,点与点关于对称轴对称,连接与对称轴交于点,求的面积;
(3)如图,点是抛物线上位于第一象限内的一点,轴,垂足为,与相交于点,
①当时,求点的坐标.
②求的最大值.
14.抛物线过,两点,与y轴相交于点C,点C、D关于抛物线的对称轴对称.
(1)求抛物线的解析式及D点坐标;
(2)在直线下方的抛物线上存在点P,使的面积最大,求出最大面积;
(3)当时,函数的最小值为5,求t的值.
15.如图,已知二次函数经过A,B两点,轴于点C,且点,,.
(1)求抛物线的解析式;
(2)点E是线段上一动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段的长度最大时,求点E的坐标.
(3)点P是抛物线对称轴上的一个动点,是否存在这样的P点,使成为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
参考答案:
1.(1);
(2)面积的最大值是
2.(1)
(2)1
3.(1)米
(2)①;②平方米
4.(1)
(2)
5.(1)
(2)当时,小花园的面积最大,最大面积是
6.(1)
(2)当绿茶的销售单价是85元/千克时,该茶庄这种绿茶在这段时间内的销售利润最大,最大利润是2450元.
7.(1),
(2)
8.(1)、、
(2)
(3)当时,有最大值2
9.(1)
(2)
10.(1)
(2)矩形菜园面积的最大值为1200平方米
11.(1)
(2)20
12.(1)二次函数解析式为
(2)当时,四边形的面积最大,最大值为,此时点P的坐标为
13.(1)抛物线的解析式为:;
(2);
(3)①;②的最大值为.
14.(1),
(2)的面积为
(3)或时,函数的最小值为5
15.(1)
(2)点E的坐标为
(3)存在;点P的坐标为或或或
1.如图在平面直角坐标系中,一次函数的图象经过点、交反比例函数的图象于点,点在反比例函数的图象上,横坐标为,轴交直线于点,连接、.
(1)求一次函数和反比例函数的表达式;
(2)求面积的最大值.
2.如图,抛物线的图象与x轴交于点A,,与y轴交于点.
(1)求抛物线的解析式.
(2)若当,取得最大值时,求m的值.
3.要在某建筑物人字形屋顶上画一幅边框是矩形的画来美化,已知,高线,如图所示.
(1)若边框是正方形,且正方形的一边在上,其余两个顶点分别在上,求正方形的边长.
(2)若要使这幅画面积最大,且矩形的一边在上,其余两个顶点分别在上,
①设,请用含的代数式表示的长;
②求此矩形的最大面积.
4.如图,抛物线与x轴相交于点,,与y轴相交于点C.
(1)求抛物线的解析式.
(2)点,是抛物线上不同的两点且,求的最小值.
5.为了改善小区环境,某小区决定在一块一边靠墙(墙长)的空地上修建一个矩形小花园,小花园一边靠墙,另三边用总长的栅栏围住,如下图所示.若设矩形小花园边的长为,面积为.
(1)求y与x之间的函数关系式;
(2)当x为何值时,小花园的面积最大?最大面积是多少?
6.中国茶文化是中国传统文化的重要组成部分之一,代表了中国文化的精髓和卓越,具有丰富的文化内涵和深远的历史意义.某茶庄经销一种绿茶,每千克成本为50元,经市场调查发现:在一段时间内,销售量W(千克)随销售单价x(元/千克)的变化而变化,具体关系式为.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x之间的函数关系式;
(2)当绿茶的销售单价是多少时,该茶庄这种绿茶在这段时间内的销售利润最大 最大利润是多少
7.如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于、点和点,一次函数的图象与抛物线交于两点.
(1)一次函数与二次函数的解析式;
(2)点是线段上的一点,过点作轴的平行线交抛物线于点,求线段的最大值.
8.如图,抛物线与轴交于点,与轴交于点和.若点是所在直线下方该抛物线上的一个动点,过点作平行于轴,交于点.
(1)求三个点,,的坐标;
(2)当点运动至抛物线的顶点时,求此时的长;
(3)设点的横坐标为,的长度为;求与之间的函数关系式,并写出的取值范围;是否存在最值,如有写出最值.
9.如图,抛物线与轴交于,两点(点在点的左侧),与轴交于点,.
(1)求抛物线的解析式;
(2)点为第四象限抛物线上一点,当值最大时,求点的坐标;
10.如图,在足够大的空地上有一段长为40米的旧墙,某人利用旧墙和木栏围成一个矩形菜园,其中,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.设矩形中,边为米,面积为平方米.
(1)求与之间的函数关系式,并写出自变量的取值范围;
(2)求矩形菜园面积的最大值.
11.发射装置距离地面15米的点处,向上发射物体,物体离地面的高度(米)与物体运动的时间(秒)之间满足函数关系,其图象如图所示,物体从发射到落地的运动时间为3秒.
(1)求此函数的解析式;
(2)求发射的物体到达最高点时距地面的高度.
12.如图,二次函数的图象交x轴于点A,B,交y轴于点C,点B的坐标为,对称轴是直线,点P是x轴上一动点,轴,交直线于点M,交抛物线于点N.
(1)求这个二次函数的解析式.
(2)若点P在线段上运动(点P与点A、点O不重合),求四边形面积的最大值,并求出此时点P的坐标.
13.如图,在平面直角坐标系中,抛物线与轴分别交于点和点,与轴交于点.
(1)求抛物线的解析式;
(2)如图,点与点关于对称轴对称,连接与对称轴交于点,求的面积;
(3)如图,点是抛物线上位于第一象限内的一点,轴,垂足为,与相交于点,
①当时,求点的坐标.
②求的最大值.
14.抛物线过,两点,与y轴相交于点C,点C、D关于抛物线的对称轴对称.
(1)求抛物线的解析式及D点坐标;
(2)在直线下方的抛物线上存在点P,使的面积最大,求出最大面积;
(3)当时,函数的最小值为5,求t的值.
15.如图,已知二次函数经过A,B两点,轴于点C,且点,,.
(1)求抛物线的解析式;
(2)点E是线段上一动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段的长度最大时,求点E的坐标.
(3)点P是抛物线对称轴上的一个动点,是否存在这样的P点,使成为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
参考答案:
1.(1);
(2)面积的最大值是
2.(1)
(2)1
3.(1)米
(2)①;②平方米
4.(1)
(2)
5.(1)
(2)当时,小花园的面积最大,最大面积是
6.(1)
(2)当绿茶的销售单价是85元/千克时,该茶庄这种绿茶在这段时间内的销售利润最大,最大利润是2450元.
7.(1),
(2)
8.(1)、、
(2)
(3)当时,有最大值2
9.(1)
(2)
10.(1)
(2)矩形菜园面积的最大值为1200平方米
11.(1)
(2)20
12.(1)二次函数解析式为
(2)当时,四边形的面积最大,最大值为,此时点P的坐标为
13.(1)抛物线的解析式为:;
(2);
(3)①;②的最大值为.
14.(1),
(2)的面积为
(3)或时,函数的最小值为5
15.(1)
(2)点E的坐标为
(3)存在;点P的坐标为或或或
同课章节目录
