2024年中考数学高频考点突破——二次函数与最大值
文档属性
| 名称 | 2024年中考数学高频考点突破——二次函数与最大值 | 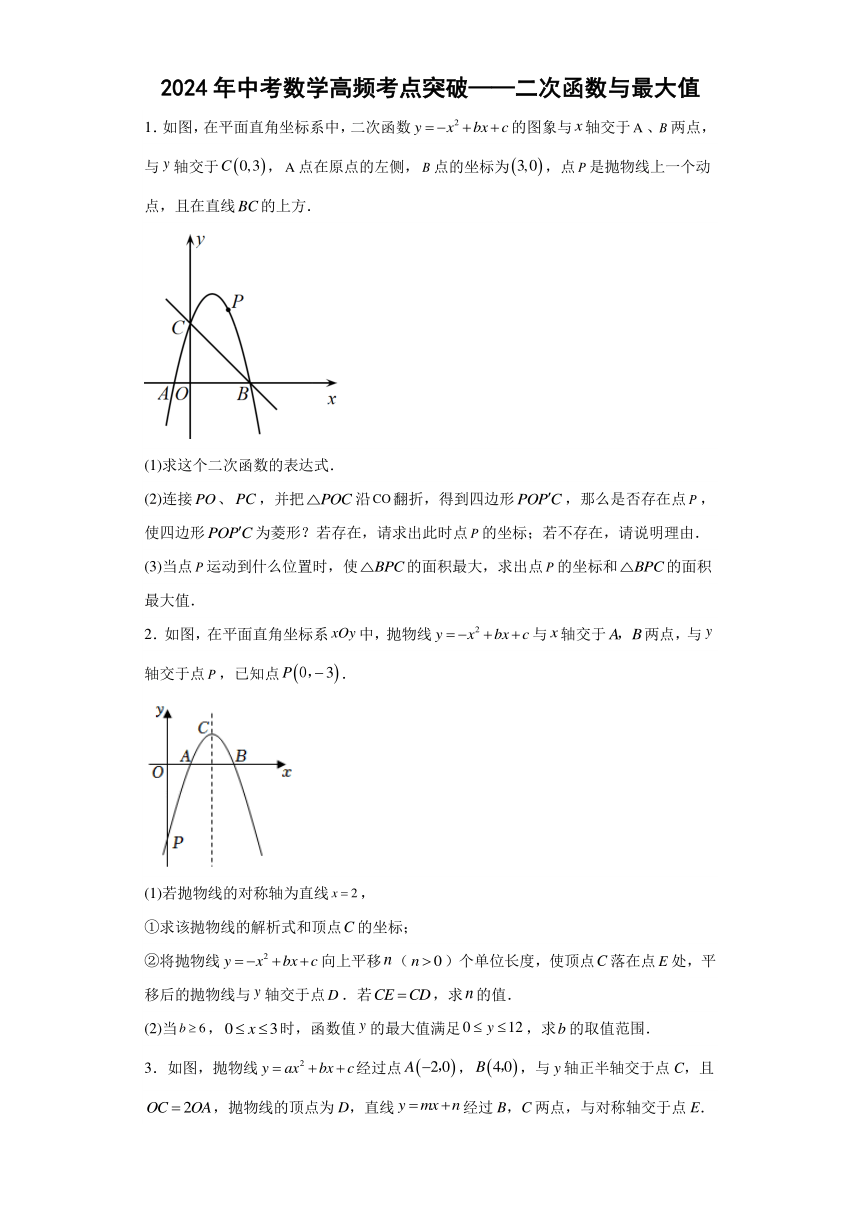 | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 18:10:27 | ||
图片预览




文档简介
2024年中考数学高频考点突破——二次函数与最大值
1.如图,在平面直角坐标系中,二次函数的图象与轴交于、两点,与轴交于,点在原点的左侧,点的坐标为,点是抛物线上一个动点,且在直线的上方.
(1)求这个二次函数的表达式.
(2)连接、,并把沿翻折,得到四边形,那么是否存在点,使四边形为菱形?若存在,请求出此时点的坐标;若不存在,请说明理由.
(3)当点运动到什么位置时,使的面积最大,求出点的坐标和的面积最大值.
2.如图,在平面直角坐标系中,抛物线与轴交于两点,与轴交于点,已知点.
(1)若抛物线的对称轴为直线,
①求该抛物线的解析式和顶点的坐标;
②将抛物线向上平移()个单位长度,使顶点落在点处,平移后的抛物线与轴交于点.若,求的值.
(2)当,时,函数值的最大值满足,求的取值范围.
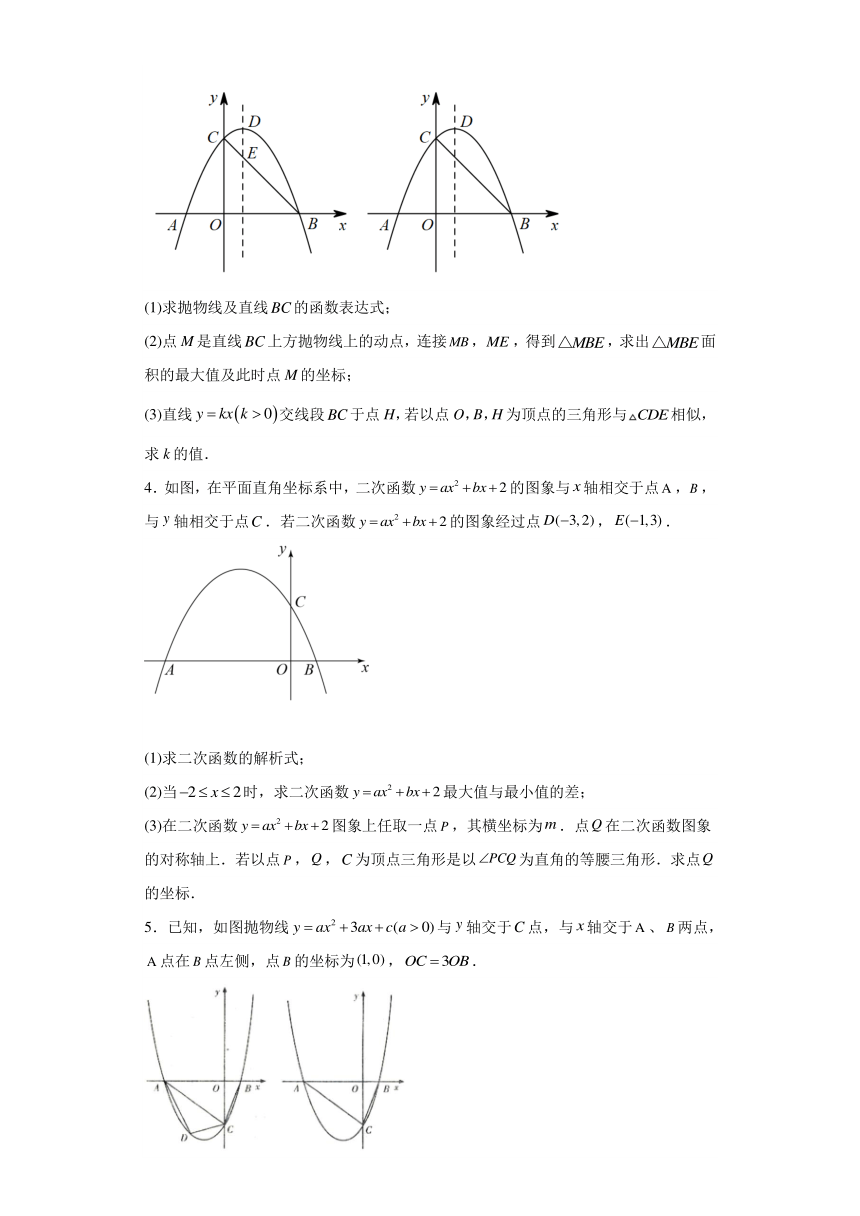
3.如图,抛物线经过点,,与y轴正半轴交于点C,且,抛物线的顶点为D,直线经过B,C两点,与对称轴交于点E.
(1)求抛物线及直线的函数表达式;
(2)点M是直线上方抛物线上的动点,连接,,得到,求出面积的最大值及此时点M的坐标;
(3)直线交线段于点H,若以点O,B,H为顶点的三角形与相似,求k的值.
4.如图,在平面直角坐标系中,二次函数的图象与轴相交于点,,与轴相交于点.若二次函数的图象经过点,.
(1)求二次函数的解析式;
(2)当时,求二次函数最大值与最小值的差;
(3)在二次函数图象上任取一点,其横坐标为.点在二次函数图象的对称轴上.若以点,,为顶点三角形是以为直角的等腰三角形.求点的坐标.
5.已知,如图抛物线与轴交于点,与轴交于、两点,点在点左侧,点的坐标为,.
(1)求抛物线的解析式;
(2)若点是线段下方抛物线上的动点,求四边形面积的最大值;
(3)若点在轴上,点在抛物线上,是否存在以为顶点且以为一边的平行四边形?若存在,求点的坐标;若不存在,请说明理由.
6.如图,抛物线与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为,,点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作轴于点D.若,的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
7.如图,已知抛物线的解析式为,抛物线与x轴交于点A和点B,与y轴交点于点C.
(1)请分别求出点A、B、C的坐标和抛物线的对称轴;
(2)连接AC、BC,将△ABC绕点B顺时针旋转90°,点A、C的对应点分别为M、N,求点M、N的坐标;
(3)若点为该抛物线上一动点,在(2)的条件下,请求出使最大时点的坐标,并请直接写出的最大值.
8.如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点,且OA=OC,连接AC.
(1)求抛物线的解析式.
(2)若点P是直线AC下方抛物线上一动点,求△ACP面积的最大值及此时点P的坐标.
(3)若点E在抛物线的对称轴上,抛物线上是否存在点F,使以A,B,E,F为顶点的四边形是平行四边形?若存在,求出所有满足条件的点F的坐标;若不存在,请说明理由.
9.如图,抛物线的对称轴为直线x=﹣1,与x轴相交于A、B两点,与y轴相交于C,OA=OC,点A的坐标为(﹣3,0).
(1)求抛物线的表达式;
(2)若点P在抛物线上,且,求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
10.在平面直角坐标系xOy中,已知抛物线经过A(4,0),B(1,4)两点.P是抛物线上一点,且在直线AB的上方.
(1)求抛物线的解析式;
(2)若△OAB面积是△PAB面积的2倍,求点P的坐标;
(3)如图,OP交AB于点C,交AB于点D.记△CDP,△CPB,△CBO的面积分别为,,.判断是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
11.抛物线过点A(-1,0),点B(3,0),与y轴交于C点.
图1 图2
(1)求抛物线的表达式及点C的坐标;
(2)如图1,设M是抛物线上的一点,若∠MAB=45°,求M点的坐标;
(3)如图2,点P在直线BC下方的抛物线上,过点P作PD⊥x轴于点D,交直线BC于点E,过P点作PF⊥BC,交BC与F点,△PEF的周长是否有最大值,若有最大值,求出此时P点的坐标.若不存在,说明理由.
12.如图,在平面直角坐标系中,已知抛物线经过,,三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,的面积为S,求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线上的动点,判断有几个位置能使以点P,Q,B,O为顶点的四边形为平行四边形(要求),直接写出相应的点Q的坐标.
13.如图,抛物线经过点,和点.
(1)求抛物线的解析式;
(2)作直线,点是线段上一个动点,过点作轴的平行线交轴于点,交抛物线于点,过点作直线的垂线,垂足为点,若设的周长为,的周长为,,点的横坐标为,请用含的代数式表示,并计算当取何值时,取得最大值;
(3)点是抛物线对称轴上的一点,若以点,,为顶点的三角形是直角三角形,请直接写出点的坐标.
14.如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能,请直接写出所有符合条件的点P坐标;若不能,请说明理由.
15.如图,的两直角边,分别在轴的负半轴和轴的正半轴上,为坐标原点,,两点的坐标分别为、,抛物线经过点,且顶点在直线上.
(1)求抛物线对应的函数关系式;
(2)若是由沿轴向右平移得到的,当四边形是菱形时,试判断点和点是否在该抛物线上,并说明理由;
(3)在(2)的条件下,若点是所在直线下方抛物线上的一个动点,过点作平行于轴交于.设点的横坐标为,的长度为.求与之间的函数关系式,写出自变量的取值范围,并求取最大值时,点的坐标.
16.如图,对称轴为直线x=-1的抛物线y=a(x-h)-4(a≠0)与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
(1)求该抛物线的解析式;
(2)若点P在抛物线上,且S△POC=4S△BOC.求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
17.如图,在直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,与y轴交于点C.
(1)写出抛物线顶点D的坐标 ;
(2)点D1是点D关于y轴的对称点,判断点D1是否在直线AC上,并说明理由;
(3)若点E是抛物线上的点,且在直线AC的上方,过点E作EF⊥x轴交线段AC于点F,求线段EF的最大值.
18.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
参考答案:
1.(1)
(2)存在,点的坐标为
(3)点的坐标为,的面积的最大值为
【分析】(1)利用待定系数法可直接求出二次函数的解析式;
(2)先设出点的坐标,再求出的坐标,利用菱形的对角线互相垂直且邻边相等即可求出点的坐标;
(3)先设出点的坐标,然后作平行轴交与点,将三角形和三角形的面积表示出来,再求出最大值的条件和最大值.
【详解】(1)解:把点,点的坐标代入,
得,
解得,
二次函数得表达式为;
(2)解:存在点,使四边形为菱形,
设,交于点,
若四边形是菱形,则,
连接,则,,
,
解得,不合题意,舍去,
点的坐标为;
(3)解:如图,过点作轴的平行线与交于点,
设,
设直线的解析式为,
则有,
解得:,
∴直线的解析式为,
则,
,
当时,的面积最大,
将代入,得,
点的坐标为,的面积的最大值为.
【点睛】本题主要考查二次函数的综合应用,关键是要会用待定系数法求抛物线的解析式,还要牢记菱形的性质:菱形的对角线互相垂直,菱形的四条边都相等,对于求三角形面积最大值的问题,一般是将三角形分割成两个三角形,即作轴的平行线或轴的平行线,然后再利用面积公式得出一个二次函数,求出顶点的纵坐标即是最大值.
2.(1)①,顶点的坐标为;②;
(2)
【分析】(1)①根据抛物线的对称轴公式即可求出解析式,由配方法可求出点的坐标;
②由题意得出,,由可得出关于的方程,解方程可得出答案;
(2)当时,确定对称轴的位置,再结合开口方向,确定当时,函数的增减性,从而得到当时,函数取最大值,再根据函数值的最大值满足,列出不等式组解答即可.
【详解】(1)解:①抛物线与轴交于,
,
抛物线的对称轴为直线,
若过点的直线是抛物线的对称轴,
则,解得:,
抛物线的解析式为,
,
顶点的坐标为;
②将抛物线向上平移()个单位长度,使顶点落在点处,
,,
,
,
,
;
(2)解:抛物线的对称轴为直线,
当时,,
抛物线开口向下,在对称轴左边,随的增大而增大,
当时,取,有最大值,
,
函数值的最大值满足,
,
解得:,
又 ,
.
【点睛】本题考查了二次函数的综合应用,二次函数的图象与性质,勾股定理的应用,平移的性质,二次函数最值问题,二次函数增减性应用等知识点,解题的关键是熟练掌握二次函数的图象与性质、平移的性质等相关知识,灵活运用数形结合思想、方程思想解决问题.
3.(1)抛物线的函数表达式为;直线的函数表达式为
(2)面积最大值为3,
(3)的值为3或2
【分析】(1)先求出C点的坐标,再利用待定系数法即可求解;
(2)先求出点B与点E之间的水平距离,再设出M点的坐标,表示出,再利用面积得到关于m的二次函数, 函数的最大值即可;
(3)先求出,得到一组对应角,再利用两个三角形相似分情况讨论,得到或,利用点的坐标得到对应线段的长度,代入求值即可.
【详解】(1)解:∵,,
∴,
∴,
∵抛物线经过点,,,
∴,
∴,
∴抛物线的函数表达式为,
∵直线经过B,C两点,
∴,
∴,
∴直线的函数表达式为.
(2)∵抛物线对称轴为直线即,
∴E点横坐标为1,
∵,
∴,
∴点B与点E之间的水平距离为,
∵点M是直线上方抛物线上的动点,
所以设,,
连接和,过M点向x轴作垂线,与交于点N,
∴,
∴,
∵面积,
设E点和B点到的距离分别为和,
∴,
该抛物线的对称轴为,图象开口向下,
∵,
∴当时,;
∵,
∴当时,;
综上可得:面积最大值为3,.
(3)将原抛物线的对称轴与x轴的交点记为T,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵以点O,B,H为顶点的三角形与相似,
∴或,
∵当时,,
∴,
∴,,
∵,
∴,或,
∵直线交线段于点H,
∴令,
解得:,
∴,
过H点向x轴作垂线,垂足为R,
∴
∵,
∴,
∴,
∴,
∴,
∴或,
∴或,
经检验,或均分别为这两个分式方程的解,且符合题意,
∴的值为3或2.
【点睛】本题考查了抛物线与一次函数的综合,涉及到了待定系数法求函数解析式、相似三角形的性质、勾股定理、两点间距离公式、等角对等边和等边对等角等知识, 解题关键是理解题意,正确做出辅助线,本题综合性较强,且要求学生具备较高的运算能力.
4.(1)
(2)
(3)或
【分析】(1)利用待定系数法即可求解;
(2)将二次函数化成顶点式为:,即抛物线的对称轴为:,即可得离抛物线对称轴越近的点的函数值越大,离抛物线对称轴越远的点的函数值越小,结合即可求出函数的最大值和最小值,问题随之得解;
(3)先求出C点坐标为:,即:,横坐标为,由点横坐标为:,可知,分情况讨论:作轴于点M,作轴于N,当M点在C点下方时,证明,即有,,即有,,可得,即有,解方程求出m的值,则Q点坐标相应可求;作轴于点M,作轴于N,当M点在C点上方时,同理可证明:,可得到,抛物线解析式化为顶点式为:,即此时二次函数的值最大为,根据,可知此时P点不存在;问题随之得解.
【详解】(1)将,代入中,
可得:,
解得:,
即二次函数解析式为:;
(2)将二次函数化成顶点式为:,
即抛物线的对称轴为:,
∵,
∴二次函数的图象开口朝下,
∴离抛物线对称轴越近的点的函数值越大,离抛物线对称轴越远的点的函数值越小,
∵,
∴当时,函数有最大值,最大值为:,
当时,函数有最小值,最小值为:,
∴函数的最大值与最小值的差为:;
(3)令时,,即C点坐标为:,
即:,
∵抛物线上点的横坐标为,
∴点坐标为,
∵点在二次函数图象的对称轴上,
∴点横坐标为:,即,
分情况讨论,
作轴于点M,作轴于N,当M点在C点下方时,如图,
∵等腰直角三角形,且,
∴,,
∵轴于点M,轴于N,
∴,,
∴,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
解得:,,
当时,,如上图,
∴,
∴,
此时Q点坐标为:;
当时,,
如图,
∴,
∴,
此时Q点坐标为:;
作轴于点M,作轴于N,当M点在C点上方时,如图,
同理可证明:,
∴,,
∵,
∴,
∵,
∴,
∴,
∵抛物线解析式化为顶点式为:,
∴此时二次函数的值最大为,
∵,
∴此时P点不存在;
综上所述:Q点坐标为:或.
【点睛】本题是一道压轴的二次函数综合题,主要考查了二次函数的图象与性质,待定系数法求解二次函数解析式,二次函数的最值问题,解一元二次方程,等腰直角三角形的性质以及全等三角形的判定与性质等知识,掌握二次函数的图象与性质,是解答本题的关键.
5.(1)
(2)13.5
(3)存在,,或
【分析】(1)根据,,求出C点坐标,把点的坐标代入,即可求出函数解析式;
(2)过点作轴分别交线段于点,设,然后求出的表达式,利用,转化为二次函数求最值;
(3)①过点作轴交抛物线于点,过点作交轴于点,此时四边形为平行四边形;②平移直线交轴于点,交轴上方的抛物线于点,由题意可知点的纵坐标为3,从而可求得其横坐标.
【详解】(1)解:∵的坐标为,
∴,
∵,点在轴下方,
∴,
∵将代入抛物线的解析式,
可得,解得,
∴抛物线的解析式为;
(2)如图1所示,过点作,交于点,
∵该抛物线的对称轴为,,
∴,
∴,
∴,
设的解析式为,
∵将代入,
可得,解得,
∴直线的解析式为,
设,则,
∵,
∴当时,有最大值,最大值为3,
∴的最大面积,
∴,
∴四边形的面积的最大值为13.5;
(3)存在,理由如下:
①如图2,过点作轴交抛物线于点,过点作交轴于点,此时四边形为平行四边形,
∵,令,
∴,
∴;
②平移直线交轴于点,交轴上方的抛物线于点,当时,四边形为平行四边形,当时,四边形为平行四边形,
∵,
∴的纵坐标均为3,
令,可得,
解得,
∴.
综上所述,存在3个点符合题意,坐标分别是,或.
【点睛】本题是二次函数综合题,涉及待定系数法求二次函数的解析式、利用二次函数求最值、平行四边形的判定与性质等知识,根据题意作出图形,利用数形结合求解是解答此题的关键.
6.(1)
(2)存在最大值,最大值为
(3)或
【分析】(1)将、代入,列方程组求出、的值即可;
(2)先求所在直线的解析式,用含的代数式表示点的坐标及的面积,求出关于的函数关系式,用函数的性质判断并求出的最值;
(3)存在符合条件的点,分三种情况根据点的位置或勾股定理列方程求出的值及点的坐标.
【详解】(1)解:把、代入,
得,
解得,
∴二次函数的解析式为.
(2)解:有最大值.理由如下:
如图1,设直线的解析式为,
,
∴该抛物线的顶点坐标为,
把、代入,得,
解得,
∴,
,
∴;
由,
得;
∵当点与点重合时,不存在以、、为顶点的三角形,
∴,
∴不存在最小值;
,
∴当时,,
∴的最大值为.
(3)解:存在,理由如下:
若,如图2,则轴,
∴,且在直线上,
∴,
解得,
∴;
若,如图3,则,
∴,
整理,得,
解得,(不符合题意,舍去);
∴,;
若,则,
∴,
整理,得,
解得,
此时不存在以,,为顶点的三角形,
∴舍去.
综上所述,点的坐标为或.
【点睛】此题重点考查二次函数的图象和性质、勾股定理、用待定系数法求函数解析式、二次根式的化简等知识,解第(3)题时应分类讨论并进行必要的检验,求出所有符合条件的点的坐标.
7.(1)A(-4,0),B(1,0),C(0,3),对称轴为直线
(2)M(1,5),N(4,1)
(3)当P的坐标为(1,0)或时,的值最大,此时最大值为
【分析】(1)提取二次项系数后分解因式,可以得出抛物线与x轴交点,令x=0代入可以得到与y轴的交点,把解析式配方后可得对称轴;
(2)根据题意作出几何图形,通过旋转性质以及通过AAS求证△OBC≌△QNB即可分别求出M、N的坐标;
(3)分析题意可得出,当P,N,B在同一直线上时,|NP-BP|的值最大,联立直线BN解析式以及抛物线解析式即可求出P的坐标.
【详解】(1)解:∵,
令x=0,则y=3,
令y=0,则,
解得x=-4或1,
∴A(-4,0),B(1,0),C(0,3),
∵,
∴对称轴为直线x=-;
(2)解:如图所示:
过N作NQ⊥x轴于点Q,
由旋转性质得MB⊥x轴,∠CBN=90°,BM=AB=5,BN=BC,
∴M(1,5),∠OBC+∠QBN=90°,
∵∠OBC+∠BCO=90°,
∴∠BCO=∠QBN,
又∵∠BOC=∠NQB=90°,BN=BC,
∴△OBC≌△QNB(AAS),
∴BQ=OC=3,NQ=OB=1,
∴OQ=1+3=4,
∴N(4,1);
(3)解:设直线NB的解析式为y=kx+b.
∵B(1,0)、N(4,1)在直线NB上,
∴,
解得:,
∴直线NB的解析式为:y=x-,
当点P,N,B在同一直线上时|NP-BP|=NB=,
当点P,N,B不在同一条直线上时|NP-BP|<NB,
∴当P,N,B在同一直线上时,|NP-BP|的值最大,
即点P为直线NB与抛物线的交点.
解方程组:,
解得:或,
∴当P的坐标为(1,0)或时,|NP-BP|的值最大,此时最大值为.
【点睛】本题属于二次函数综合题,考查待定系数法,旋转性质,全等三角形的判定与性质等知识,本题的关键是数形相结合,以及正确讨论出当P,N,B在同一直线上时,|NP-BP|的值最大是解题的关键.
8.(1)
(2)当时,△ACP面积的最大值为,此时点;
(3)点F的坐标为(﹣5,12)或(3,12)或(﹣1,﹣4)
【分析】(1)利用抛物线的解析式令时,求得点的坐标,再利用OA=OC,求得点的坐标,代入抛物线的解析式即可求解;
(2)过点P作轴交AC于点H,利用即可求解;
(3)分AB是边、AB是对角线两种情况,利用图形平移的性质和中点公式,即可求解.
【详解】(1)解:∵抛物线的解析式为,
∴当时,,
∴(0,-3)
故OC=3=OA,
∴A(﹣3,0),
将点A的坐标代入抛物线表达式得:9a﹣6a﹣3=0,解得a=1,
故抛物线的表达式为;
(2)设直线AC的表达式为,
∵直线AC过点(0,-3),A(﹣3,0),
∴,解得
∴直线AC的表达式为y=﹣x﹣3,
过点P作轴交AC于点H,
设点P(x,),则点H(x,﹣x﹣3),
∴,
则
,
∵<0,故△ACP面积有最大值,当时,△ACP面积的最大值为,
∴当时,
此时点P(,);
(3)对于,令y=0,
即,
解得x=﹣3或1,
故点B(1,0),
∴抛物线的对称轴为直线为x=﹣1,
设点F(m,n),即n=m2+2m﹣3①,点E(﹣1,t),
①当AB是边时,
点A向右平移4个单位得到点B,同样点F(E)向右平移4个单位得到点E(F),
即m±4=﹣1②,
联立①②并解得或,
故点F的坐标为(﹣5,12)或(3,12);
②当AB是对角线时,A(﹣3,0),B(1,0),
由中点公式得:③,
联立①③并解得,
故点F的坐标为(﹣1,﹣4);
综上,点F的坐标为(﹣5,12)或(3,12)或(﹣1,﹣4).
【点睛】本题考查的是二次函数综合运用,涉及到一次函数的性质、平行四边形的性质、中点坐标公式的运用、图形的平移等,其中(3),要注意分类求解,避免遗漏.
9.(1)
(2)P(4,21),(﹣4,5)
(3)
【分析】(1)根据OA=OC,可求c;再依据对称轴是直线x=﹣1,点A的坐标为(﹣3,0),可求a、b,即得求抛物线解析式.
(2)可求△BOC的面积,根据,可求P点坐标.
(3)求出直线AC解析式,设点Q(m,﹣m﹣3)(﹣3≤m≤0),则点D,根据二次函数的最值求法,可求QD的最大值.
【详解】(1)令x=0,则y=c,
∴OC=﹣c,
∵OA=OC,
∴3=﹣c,即c=﹣3.
∵对称轴是直线x=﹣1,点A的坐标为(﹣3,0),
根据题意得:,
解之:.
∴抛物线解析式.
(2)当x=0时,y=﹣3,
∴点C(0,﹣3),即OC=3,
∵A,B关于对称轴对称,
∴B(1,0),即OB=1,
∴,
设,
∴=×3×|x|,
∵=,
∴,
∴x=±4,
∴P(4,21),(﹣4,5).
(3)∵点A(﹣3,0),点C(0,﹣3),
∴直线AC解析式y=﹣x﹣3,
∴设点Q(m,﹣m﹣3)(﹣3≤m≤0),
则点,
∴,
∴当m=﹣时,QD的最大值为 .
【点睛】本题考查了二次函数的综合题,待定系数法求解析式,二次函数的最值问题,利用数形结合思想解决问题是本题的关键
10.(1)
(2)存在,或(3,4)
(3)存在,
【分析】(1)待定系数法求解析式即可求解;
(2)待定系数法求得直线AB的解析式为,过点P作PM⊥x轴,垂足为M,PM交AB于点N.过点B作BE⊥PM,垂足为E.可得,设,则.由,解方程求得的值,进而即可求解;
(3)由已知条件可得,进而可得,过点分别作轴的垂线,垂足分别,交于点,过作的平行线,交于点,可得,设,,则,根据可得,根据,根据二次函数的性质即可求的最大值.
【详解】(1)解:(1)将A(4,0),B(1,4)代入,
得,
解得.
所以抛物线的解析式为.
(2)设直线AB的解析式为,
将A(4,0),B(1,4)代入,
得,
解得.
所以直线AB的解析式为.
过点P作PM⊥x轴,垂足为M,PM交AB于点N.
过点B作BE⊥PM,垂足为E.
所以
.
因为A(4,0),B(1,4),所以.
因为△OAB的面积是△PAB面积的2倍,
所以,.
设,则.
所以,
即,
解得,.
所以点P的坐标为或(3,4).
(3)
记△CDP,△CPB,△CBO的面积分别为,,.则
如图,过点分别作轴的垂线,垂足分别,交于点,过作的平行线,交于点
,
,
设
直线AB的解析式为.
设,则
整理得
时,取得最大值,最大值为
【点睛】本题考查了二次函数综合,待定系数法求解析式,面积问题,相似三角形的性质与判定,第三问中转化为线段的比是解题的关键.
11.(1),C(0,-3)
(2)M(4,5)或M(2,-3)
(3)有,P点的坐标为(,-)
【分析】(1)把点的坐标代入解析式,转化为方程组,确定a,b的值即可.
(2)分点M在第一象限和第四象限两种情况根据45度角的特征列方程求解即可.
(3)根据垂直及对顶角相等易证△FPE∽△OBC,根据相似三角形的性质将题转化为与△OBC的周长有关的比例式;设直线BC的解析式为y=px+q,根据待定系数法求出直线BC的解析式,设P(n,),则E(n,n-3),列出关于n的二次函数式,根据二次函数最值即可得出答案.
【详解】(1)由题意得
,
解得,
∴抛物线的解析式为,
∴点C(0,-3).
(2)①当M点在第一象限时,
设M(m,),
过M点作MN⊥x轴,
∵∠MAB=45°,MN=NA,
∴m+1=,
解方程得:m=4或m=-1,
m=-1不合题意,舍去.
故m=4 ,
∴M(4,5);
当M点在第四象限时,同理可得:
m+1=-()
解方程得:m=2或m=-1,
m=-1不合题意,舍去.
故m=2,
∴M(2,-3),
综上M(4,5)或M(2,-3).
(3)△PEF的周长有最大值.理由如下:
∵PD⊥DB,
∴∠EBD=90°-∠DEB,
∵PF⊥BC,
∴∠FPE=90°-∠FEP,
∵∠DEB=∠FEP,
∴∠EBD=∠FPE,
又∵∠EFP=∠BOC=90°,
∴△FPE∽△OBC,
∴△PEF的周长:△OBC的周长=PE:BC,
∵OB=OC=3,
∴BC=,
∴△PEF的周长为z,△OBC的周长=,
∵直线BC过B(3,0)和C(0,-3),
设直线BC的解析式为y=px+q,
∴,
解得,
∴直线BC的解析式为y=x-3,
设P(n,),则E(n,n-3)
PE=n-3-()=,
∴z:(6+3)=():3,
z=-(+1) +3(+1)n,
∵-(+1)<0,
∴z有最大值,此时n=,
当n=时,=-,
故P点的坐标为(,-).
【点睛】本题考查了待定系数法确定函数的解析式,解方程,三角形相似的判断和性质,二次函数的最值,熟练掌握二次函数的最值是解题的关键.
12.(1)
(2)S的最大值为4
(3)或或.
【分析】(1)先假设出函数解析式,利用待定系数法求解函数解析式即可;
(2)设出M点的坐标,利用,即可进行解答;
(3)由,则,是平行四边形的边,根据平行四边形的对边相等,列出方程求解即可.
【详解】(1)解:设此抛物线的函数解析式为:,
将,,三点代入函数解析式得:
,
解得,
所以此函数解析式为:;
(2)解:连接 ,
∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为,
∴
,
∵,
当时,S有最大值为:.
(3)解:设,
根据平行四边形的性质知,且,则,为平行四边形的边,
∴Q的横坐标等于P的横坐标,
又∵直线的解析式为,
则,
由,得,
整理得:
所以或
解得或或(不符合题意,舍去),
∵,
∴不可能是对角线
∴由此可得:或或.
【点睛】本题考查的是二次函数综合运用,涉及到平行四边形的性质、面积的计算等,有一定的综合性,熟练的利用二次函数的性质与平行四边形的性质解题是关键.
13.(1)抛物线的关系式为;(2),当时,取得最大值;(3)点的坐标为或或或.
【分析】(1)将点A(,),B(,)分别代入抛物线的关系式中,即可求解;
(2)先求得的周长,证得,,利用相似三角形的性质得到二次函数的关系式,再利用二次函数的性质即可求解;
(3)分三种情形分别求解①当∠BCP=90°,②当∠CBP=90°,③当∠BPC=90°时,根据勾股定理列出方程即可.
【详解】(1)将点,分别代入抛物线的关系式中,得
解得,
∴抛物线的关系式为;
(2)令 ,则,
∴点C的坐标为(,),
∵点B的坐标为(,),
∴OB=3,OC=4,BC=,
∴的周长为,
设直线的关系式为,
把点B的坐标为(,)代入得:,
∴直线的关系式为,
∵点的横坐标为,
∴,,
∵轴,
∴,
∴,
∵,,
∴,
∴,
∴,,
∴,,
即,
∵,
∴当时,取得最大值;
(3)抛物线的关系式为,
∴抛物线的对称轴为:,
∴设点P的坐标为(1,m),
∴,
,
,
①当∠BCP=90°时,
∵,即,
解得:,
∴点P的坐标为(1,);
②当∠CBP=90°时,
∵,即,
解得:,
∴点P的坐标为(1,);
③当∠BPC=90°时,
∵,即,
解得:或
∴点P的坐标为(1,)或(1,);
综上,点的坐标为(1,)或(1,)或(1,)或(1,).
【点睛】本题是二次函数综合题,考查了待定系数法求函数解析式,二次函数的性质,相似三角形的判定和性质,勾股定理的应用等知识,解题的关键是学会构建二次函数解决最值问题,学会用分类讨论的思想思考问题,属于中考压轴题.
14.(1)y=x2-4x+3;(2)点P在运动的过程中,线段PD长度的最大值为;(3)能,点P的坐标为:(1,0)或(2,-1).
【分析】(1)把点A、B的坐标代入抛物线解析式,解方程组得到b、c的值,即可得解;
(2)求出点C的坐标,再利用待定系数法求出直线AC的解析式,再根据抛物线解析式设出点P的坐标,然后表示出PD的长度,再根据二次函数的最值问题解答;
(3)分情况讨论①∠APD是直角时,点P与点B重合,②求出抛物线顶点坐标,然后判断出点P为在抛物线顶点时,∠PAD是直角,分别写出点P的坐标即可;
【详解】(1)把点A(3,0)和点B(1,0)代入抛物线y=x2+bx+c,
得:
解得
∴y=x2-4x+3.
(2)把x=0代入y=x2-4x+3,得y=3.
∴C(0,3).
又∵A(3,0),
设直线AC的解析式为:y=kx+m,
把点A,C的坐标代入得:
∴直线AC的解析式为:y=-x+3.
PD=-x+3- (x2-4x+3)=-x2+3x=+.
∵0∴x=时,PD最大为.
即点P在运动的过程中,线段PD长度的最大值为.
(3)①∠APD是直角时,点P与点B重合,
此时,点P(1,0),
②∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的顶点坐标为(2,﹣1),
∵A(3,0),
∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,
此时,点P(2,﹣1),
综上所述,点P(1,0)或(2,﹣1)时,△APD能构成直角三角形;
【点睛】本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,二次函数的最值问题,二次函数的对称性以及顶点坐标的求解,直角三角形存在性问题时需要分类讨论.
15.(1);(2)在,理由见解析;(3)s=,时,最大,点的坐标为.
【分析】(1)已知了抛物线上A、B点的坐标以及抛物线的对称轴方程,可用待定系数法求出抛物线的解析式.(2)首先求出AB的长,将A、B的坐标向右平移AB个单位,即可得出C、D的坐标,再代入抛物线的解析式中进行验证即可.(3)根据C、D的坐标,易求得直线CD的解析式;那么线段MN的长实际是直线BC与抛物线的函数值的差,可将x=t代入两个函数的解析式中,得出的两函数值的差即为l的表达式,由此可求出l、t的函数关系式,根据所得函数的性质即可求出l取最大值时,点M的坐标.
【详解】(1)∵的顶点在直线上,
∴可设所求抛物线对应的函数关系式为,
∴点在此抛物线上,
∴,
∴,
∴所求函数关系式为:;
(2)在中,,,
∴,
∵四边形是菱形,
∴,
∵两点的坐标分别是、,
∴两点的坐标分别是、;
当时,;
当时,;
∴点和点在所求抛物线上;
(3)设直线对应的函数关系式为,
则,
解得:;
∴.
∵轴,点点的横坐标为,
∴点的横坐标也为;
则,,
∴
,
∵,
∴当时,最大,此时.
此时点的坐标为.
【点睛】本题考查待定系数法求一次函数、二次函数解析式、菱形的性质、图象的平移变换,等知识.熟练掌握待定系数法是解题的关键.
16.(1)所求抛物线的解析式是;
(2)点的坐标为,或;
(3)如当时,有最大值.
【分析】(1)因为抛物线的对称轴为,可得h值;点坐标为在抛物线上,代入抛物线的解析式,即可解答;
(2)先由二次函数的解析式为,得到点坐标,然后设点坐标为,根据列出关于的方程,解方程求出的值,进而得到点的坐标;
(3)先运用待定系数法求出直线的解析式为,再设点坐标为,则点坐标为,然后用含的代数式表示,根据二次函数的性质即可求出线段长度的最大值.
【详解】(1)由题意对称轴为直线,
设抛物线解析式为,把点代入得,
.
∴所求抛物线的解析式是.
(2)如图1.
,当时,.所以点,.
令,解得,或.点,.
设点.
此时.
.
由得.
解得或.
所以或.
所以点的坐标为,或.
(3)如图2.
设直线的解析式为:.
把,代入得,解得.
所以直线AC的解析式为.
设点,点.
所以.
所以当时,有最大值.
【点睛】此题考查了待定系数法求二次函数、一次函数的解析式,二次函数的性质以及三角形面积、线段长度问题.此题难度适中,解题的关键是运用方程思想与数形结合思想.
17.(1) (﹣1,4);(2)见解析;(3) 2.25.
【分析】(1)根据二次函数的解析式直接写出即可;
(2)先根据二次函数求出A、C的坐标,再用待定系数法确定直线AC的关系式,再求出
点D1,把它代入直线判断是否再直线上;
(3)设点E(x,﹣x2﹣2x+3),F(x,x+3),则EF=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+1.5)2+2.25, 则可知x=-1.5时,EF的最大值2.25.
【详解】解:(1)∵y=﹣(x+1)2+4,
∴抛物线顶点D的坐标是(﹣1,4).
故答案为(﹣1,4);
(2)点D1在直线AC上,理由如下:
∵抛物线y=﹣(x+1)2+4与x轴交于点A、B,与y轴交于点C,
∴当y=0时,﹣(x+1)2+4=0,解得x=1或﹣3,A(﹣3,0),B(1,0),
当x=0时,y=﹣1+4=3,C(0,3).
设直线AC的解析式为y=kx+b,
由题意得,解得,
∴直线AC的解析式为y=x+3.
∵点D1是点D关于y轴的对称点,D(﹣1,4).
∴D1(1,4),
∵x=1时,y=1+3=4,
∴点D1在直线AC上;
(3)设点E(x,﹣x2﹣2x+3),则F(x,x+3),
∵EF=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+1.5)2+2.25,
∴线段EF的最大值是2.25.
【点睛】此题主要考查二次函数的图像,根据题意求出与坐标轴的交点是解题的关键.
18.(1)y=﹣x2﹣2x+3;y=﹣x+1;(2)当x=﹣时,△APC的面积取最大值,最大值为,此时点P的坐标为(﹣,);(3)在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为3.
【分析】(1)根据点A,C的坐标,利用待定系数法即可求出抛物线及直线AC的函数关系式;(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,设点P的坐标为(x,﹣x2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),进而可得出PF的值,由点C的坐标可得出点Q的坐标,进而可得出AQ的值,利用三角形的面积公式可得出S△APC=﹣x2﹣x+3,再利用二次函数的性质,即可解决最值问题;(3)利用二次函数图象上点的坐标特征可得出点N的坐标,利用配方法可找出抛物线的对称轴,由点C,N的坐标可得出点C,N关于抛物线的对称轴对称,令直线AC与抛物线的对称轴的交点为点M,则此时△ANM周长取最小值,再利用一次函数图象上点的坐标特征求出点M的坐标,以及利用两点间的距离公式结合三角形的周长公式求出△ANM周长的最小值即可得出结论.
【详解】(1)将A(1,0),C(﹣2,3)代入y=﹣x2+bx+c,得:
,解得:,
∴抛物线的函数关系式为y=﹣x2﹣2x+3;
设直线AC的函数关系式为y=mx+n(m≠0),
将A(1,0),C(﹣2,3)代入y=mx+n,得:
,解得:,
∴直线AC的函数关系式为y=﹣x+1.
(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,如图1所示.
设点P的坐标为(x,﹣x2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),
∴PE=﹣x2﹣2x+3,EF=﹣x+1,EF=PE﹣EF=﹣x2﹣2x+3﹣(﹣x+1)=﹣x2﹣x+2.
∵点C的坐标为(﹣2,3),
∴点Q的坐标为(﹣2,0),
∴AQ=1﹣(﹣2)=3,
∴S△APC=AQ PF=﹣x2﹣x+3=﹣(x+)2+ .
∵﹣<0,
∴当x=﹣时,△APC的面积取最大值,最大值为,此时点P的坐标为(﹣, ).
(3)当x=0时,y=﹣x2﹣2x+3=3,
∴点N的坐标为(0,3).
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的对称轴为直线x=﹣1.
∵点C的坐标为(﹣2,3),
∴点C,N关于抛物线的对称轴对称.
令直线AC与抛物线的对称轴的交点为点M,如图2所示.
∵点C,N关于抛物线的对称轴对称,
∴MN=CM,
∴AM+MN=AM+MC=AC,
∴此时△ANM周长取最小值.
当x=﹣1时,y=﹣x+1=2,
∴此时点M的坐标为(﹣1,2).
∵点A的坐标为(1,0),点C的坐标为(﹣2,3),点N的坐标为(0,3),
∴AC= =3,AN= =,
∴C△ANM=AM+MN+AN=AC+AN=3+.
∴在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为3+.
【点睛】本题考查待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图象上点的坐标特征、一次函数图象上点的坐标特征、二次函数的性质、三角形的面积以及周长,解题的关键是:(1)根据点的坐标,利用待定系数法求出抛物线及直线AC的函数关系式;(2)利用三角形的面积公式找出S△APC=﹣x2﹣x+3的最值;(3)利用二次函数图象的对称性结合两点之间线段最短找出点M的位置.
1.如图,在平面直角坐标系中,二次函数的图象与轴交于、两点,与轴交于,点在原点的左侧,点的坐标为,点是抛物线上一个动点,且在直线的上方.
(1)求这个二次函数的表达式.
(2)连接、,并把沿翻折,得到四边形,那么是否存在点,使四边形为菱形?若存在,请求出此时点的坐标;若不存在,请说明理由.
(3)当点运动到什么位置时,使的面积最大,求出点的坐标和的面积最大值.
2.如图,在平面直角坐标系中,抛物线与轴交于两点,与轴交于点,已知点.
(1)若抛物线的对称轴为直线,
①求该抛物线的解析式和顶点的坐标;
②将抛物线向上平移()个单位长度,使顶点落在点处,平移后的抛物线与轴交于点.若,求的值.
(2)当,时,函数值的最大值满足,求的取值范围.
3.如图,抛物线经过点,,与y轴正半轴交于点C,且,抛物线的顶点为D,直线经过B,C两点,与对称轴交于点E.
(1)求抛物线及直线的函数表达式;
(2)点M是直线上方抛物线上的动点,连接,,得到,求出面积的最大值及此时点M的坐标;
(3)直线交线段于点H,若以点O,B,H为顶点的三角形与相似,求k的值.
4.如图,在平面直角坐标系中,二次函数的图象与轴相交于点,,与轴相交于点.若二次函数的图象经过点,.
(1)求二次函数的解析式;
(2)当时,求二次函数最大值与最小值的差;
(3)在二次函数图象上任取一点,其横坐标为.点在二次函数图象的对称轴上.若以点,,为顶点三角形是以为直角的等腰三角形.求点的坐标.
5.已知,如图抛物线与轴交于点,与轴交于、两点,点在点左侧,点的坐标为,.
(1)求抛物线的解析式;
(2)若点是线段下方抛物线上的动点,求四边形面积的最大值;
(3)若点在轴上,点在抛物线上,是否存在以为顶点且以为一边的平行四边形?若存在,求点的坐标;若不存在,请说明理由.
6.如图,抛物线与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为,,点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作轴于点D.若,的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
7.如图,已知抛物线的解析式为,抛物线与x轴交于点A和点B,与y轴交点于点C.
(1)请分别求出点A、B、C的坐标和抛物线的对称轴;
(2)连接AC、BC,将△ABC绕点B顺时针旋转90°,点A、C的对应点分别为M、N,求点M、N的坐标;
(3)若点为该抛物线上一动点,在(2)的条件下,请求出使最大时点的坐标,并请直接写出的最大值.
8.如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点,且OA=OC,连接AC.
(1)求抛物线的解析式.
(2)若点P是直线AC下方抛物线上一动点,求△ACP面积的最大值及此时点P的坐标.
(3)若点E在抛物线的对称轴上,抛物线上是否存在点F,使以A,B,E,F为顶点的四边形是平行四边形?若存在,求出所有满足条件的点F的坐标;若不存在,请说明理由.
9.如图,抛物线的对称轴为直线x=﹣1,与x轴相交于A、B两点,与y轴相交于C,OA=OC,点A的坐标为(﹣3,0).
(1)求抛物线的表达式;
(2)若点P在抛物线上,且,求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
10.在平面直角坐标系xOy中,已知抛物线经过A(4,0),B(1,4)两点.P是抛物线上一点,且在直线AB的上方.
(1)求抛物线的解析式;
(2)若△OAB面积是△PAB面积的2倍,求点P的坐标;
(3)如图,OP交AB于点C,交AB于点D.记△CDP,△CPB,△CBO的面积分别为,,.判断是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
11.抛物线过点A(-1,0),点B(3,0),与y轴交于C点.
图1 图2
(1)求抛物线的表达式及点C的坐标;
(2)如图1,设M是抛物线上的一点,若∠MAB=45°,求M点的坐标;
(3)如图2,点P在直线BC下方的抛物线上,过点P作PD⊥x轴于点D,交直线BC于点E,过P点作PF⊥BC,交BC与F点,△PEF的周长是否有最大值,若有最大值,求出此时P点的坐标.若不存在,说明理由.
12.如图,在平面直角坐标系中,已知抛物线经过,,三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,的面积为S,求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线上的动点,判断有几个位置能使以点P,Q,B,O为顶点的四边形为平行四边形(要求),直接写出相应的点Q的坐标.
13.如图,抛物线经过点,和点.
(1)求抛物线的解析式;
(2)作直线,点是线段上一个动点,过点作轴的平行线交轴于点,交抛物线于点,过点作直线的垂线,垂足为点,若设的周长为,的周长为,,点的横坐标为,请用含的代数式表示,并计算当取何值时,取得最大值;
(3)点是抛物线对称轴上的一点,若以点,,为顶点的三角形是直角三角形,请直接写出点的坐标.
14.如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能,请直接写出所有符合条件的点P坐标;若不能,请说明理由.
15.如图,的两直角边,分别在轴的负半轴和轴的正半轴上,为坐标原点,,两点的坐标分别为、,抛物线经过点,且顶点在直线上.
(1)求抛物线对应的函数关系式;
(2)若是由沿轴向右平移得到的,当四边形是菱形时,试判断点和点是否在该抛物线上,并说明理由;
(3)在(2)的条件下,若点是所在直线下方抛物线上的一个动点,过点作平行于轴交于.设点的横坐标为,的长度为.求与之间的函数关系式,写出自变量的取值范围,并求取最大值时,点的坐标.
16.如图,对称轴为直线x=-1的抛物线y=a(x-h)-4(a≠0)与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
(1)求该抛物线的解析式;
(2)若点P在抛物线上,且S△POC=4S△BOC.求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
17.如图,在直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,与y轴交于点C.
(1)写出抛物线顶点D的坐标 ;
(2)点D1是点D关于y轴的对称点,判断点D1是否在直线AC上,并说明理由;
(3)若点E是抛物线上的点,且在直线AC的上方,过点E作EF⊥x轴交线段AC于点F,求线段EF的最大值.
18.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
参考答案:
1.(1)
(2)存在,点的坐标为
(3)点的坐标为,的面积的最大值为
【分析】(1)利用待定系数法可直接求出二次函数的解析式;
(2)先设出点的坐标,再求出的坐标,利用菱形的对角线互相垂直且邻边相等即可求出点的坐标;
(3)先设出点的坐标,然后作平行轴交与点,将三角形和三角形的面积表示出来,再求出最大值的条件和最大值.
【详解】(1)解:把点,点的坐标代入,
得,
解得,
二次函数得表达式为;
(2)解:存在点,使四边形为菱形,
设,交于点,
若四边形是菱形,则,
连接,则,,
,
解得,不合题意,舍去,
点的坐标为;
(3)解:如图,过点作轴的平行线与交于点,
设,
设直线的解析式为,
则有,
解得:,
∴直线的解析式为,
则,
,
当时,的面积最大,
将代入,得,
点的坐标为,的面积的最大值为.
【点睛】本题主要考查二次函数的综合应用,关键是要会用待定系数法求抛物线的解析式,还要牢记菱形的性质:菱形的对角线互相垂直,菱形的四条边都相等,对于求三角形面积最大值的问题,一般是将三角形分割成两个三角形,即作轴的平行线或轴的平行线,然后再利用面积公式得出一个二次函数,求出顶点的纵坐标即是最大值.
2.(1)①,顶点的坐标为;②;
(2)
【分析】(1)①根据抛物线的对称轴公式即可求出解析式,由配方法可求出点的坐标;
②由题意得出,,由可得出关于的方程,解方程可得出答案;
(2)当时,确定对称轴的位置,再结合开口方向,确定当时,函数的增减性,从而得到当时,函数取最大值,再根据函数值的最大值满足,列出不等式组解答即可.
【详解】(1)解:①抛物线与轴交于,
,
抛物线的对称轴为直线,
若过点的直线是抛物线的对称轴,
则,解得:,
抛物线的解析式为,
,
顶点的坐标为;
②将抛物线向上平移()个单位长度,使顶点落在点处,
,,
,
,
,
;
(2)解:抛物线的对称轴为直线,
当时,,
抛物线开口向下,在对称轴左边,随的增大而增大,
当时,取,有最大值,
,
函数值的最大值满足,
,
解得:,
又 ,
.
【点睛】本题考查了二次函数的综合应用,二次函数的图象与性质,勾股定理的应用,平移的性质,二次函数最值问题,二次函数增减性应用等知识点,解题的关键是熟练掌握二次函数的图象与性质、平移的性质等相关知识,灵活运用数形结合思想、方程思想解决问题.
3.(1)抛物线的函数表达式为;直线的函数表达式为
(2)面积最大值为3,
(3)的值为3或2
【分析】(1)先求出C点的坐标,再利用待定系数法即可求解;
(2)先求出点B与点E之间的水平距离,再设出M点的坐标,表示出,再利用面积得到关于m的二次函数, 函数的最大值即可;
(3)先求出,得到一组对应角,再利用两个三角形相似分情况讨论,得到或,利用点的坐标得到对应线段的长度,代入求值即可.
【详解】(1)解:∵,,
∴,
∴,
∵抛物线经过点,,,
∴,
∴,
∴抛物线的函数表达式为,
∵直线经过B,C两点,
∴,
∴,
∴直线的函数表达式为.
(2)∵抛物线对称轴为直线即,
∴E点横坐标为1,
∵,
∴,
∴点B与点E之间的水平距离为,
∵点M是直线上方抛物线上的动点,
所以设,,
连接和,过M点向x轴作垂线,与交于点N,
∴,
∴,
∵面积,
设E点和B点到的距离分别为和,
∴,
该抛物线的对称轴为,图象开口向下,
∵,
∴当时,;
∵,
∴当时,;
综上可得:面积最大值为3,.
(3)将原抛物线的对称轴与x轴的交点记为T,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵以点O,B,H为顶点的三角形与相似,
∴或,
∵当时,,
∴,
∴,,
∵,
∴,或,
∵直线交线段于点H,
∴令,
解得:,
∴,
过H点向x轴作垂线,垂足为R,
∴
∵,
∴,
∴,
∴,
∴,
∴或,
∴或,
经检验,或均分别为这两个分式方程的解,且符合题意,
∴的值为3或2.
【点睛】本题考查了抛物线与一次函数的综合,涉及到了待定系数法求函数解析式、相似三角形的性质、勾股定理、两点间距离公式、等角对等边和等边对等角等知识, 解题关键是理解题意,正确做出辅助线,本题综合性较强,且要求学生具备较高的运算能力.
4.(1)
(2)
(3)或
【分析】(1)利用待定系数法即可求解;
(2)将二次函数化成顶点式为:,即抛物线的对称轴为:,即可得离抛物线对称轴越近的点的函数值越大,离抛物线对称轴越远的点的函数值越小,结合即可求出函数的最大值和最小值,问题随之得解;
(3)先求出C点坐标为:,即:,横坐标为,由点横坐标为:,可知,分情况讨论:作轴于点M,作轴于N,当M点在C点下方时,证明,即有,,即有,,可得,即有,解方程求出m的值,则Q点坐标相应可求;作轴于点M,作轴于N,当M点在C点上方时,同理可证明:,可得到,抛物线解析式化为顶点式为:,即此时二次函数的值最大为,根据,可知此时P点不存在;问题随之得解.
【详解】(1)将,代入中,
可得:,
解得:,
即二次函数解析式为:;
(2)将二次函数化成顶点式为:,
即抛物线的对称轴为:,
∵,
∴二次函数的图象开口朝下,
∴离抛物线对称轴越近的点的函数值越大,离抛物线对称轴越远的点的函数值越小,
∵,
∴当时,函数有最大值,最大值为:,
当时,函数有最小值,最小值为:,
∴函数的最大值与最小值的差为:;
(3)令时,,即C点坐标为:,
即:,
∵抛物线上点的横坐标为,
∴点坐标为,
∵点在二次函数图象的对称轴上,
∴点横坐标为:,即,
分情况讨论,
作轴于点M,作轴于N,当M点在C点下方时,如图,
∵等腰直角三角形,且,
∴,,
∵轴于点M,轴于N,
∴,,
∴,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
解得:,,
当时,,如上图,
∴,
∴,
此时Q点坐标为:;
当时,,
如图,
∴,
∴,
此时Q点坐标为:;
作轴于点M,作轴于N,当M点在C点上方时,如图,
同理可证明:,
∴,,
∵,
∴,
∵,
∴,
∴,
∵抛物线解析式化为顶点式为:,
∴此时二次函数的值最大为,
∵,
∴此时P点不存在;
综上所述:Q点坐标为:或.
【点睛】本题是一道压轴的二次函数综合题,主要考查了二次函数的图象与性质,待定系数法求解二次函数解析式,二次函数的最值问题,解一元二次方程,等腰直角三角形的性质以及全等三角形的判定与性质等知识,掌握二次函数的图象与性质,是解答本题的关键.
5.(1)
(2)13.5
(3)存在,,或
【分析】(1)根据,,求出C点坐标,把点的坐标代入,即可求出函数解析式;
(2)过点作轴分别交线段于点,设,然后求出的表达式,利用,转化为二次函数求最值;
(3)①过点作轴交抛物线于点,过点作交轴于点,此时四边形为平行四边形;②平移直线交轴于点,交轴上方的抛物线于点,由题意可知点的纵坐标为3,从而可求得其横坐标.
【详解】(1)解:∵的坐标为,
∴,
∵,点在轴下方,
∴,
∵将代入抛物线的解析式,
可得,解得,
∴抛物线的解析式为;
(2)如图1所示,过点作,交于点,
∵该抛物线的对称轴为,,
∴,
∴,
∴,
设的解析式为,
∵将代入,
可得,解得,
∴直线的解析式为,
设,则,
∵,
∴当时,有最大值,最大值为3,
∴的最大面积,
∴,
∴四边形的面积的最大值为13.5;
(3)存在,理由如下:
①如图2,过点作轴交抛物线于点,过点作交轴于点,此时四边形为平行四边形,
∵,令,
∴,
∴;
②平移直线交轴于点,交轴上方的抛物线于点,当时,四边形为平行四边形,当时,四边形为平行四边形,
∵,
∴的纵坐标均为3,
令,可得,
解得,
∴.
综上所述,存在3个点符合题意,坐标分别是,或.
【点睛】本题是二次函数综合题,涉及待定系数法求二次函数的解析式、利用二次函数求最值、平行四边形的判定与性质等知识,根据题意作出图形,利用数形结合求解是解答此题的关键.
6.(1)
(2)存在最大值,最大值为
(3)或
【分析】(1)将、代入,列方程组求出、的值即可;
(2)先求所在直线的解析式,用含的代数式表示点的坐标及的面积,求出关于的函数关系式,用函数的性质判断并求出的最值;
(3)存在符合条件的点,分三种情况根据点的位置或勾股定理列方程求出的值及点的坐标.
【详解】(1)解:把、代入,
得,
解得,
∴二次函数的解析式为.
(2)解:有最大值.理由如下:
如图1,设直线的解析式为,
,
∴该抛物线的顶点坐标为,
把、代入,得,
解得,
∴,
,
∴;
由,
得;
∵当点与点重合时,不存在以、、为顶点的三角形,
∴,
∴不存在最小值;
,
∴当时,,
∴的最大值为.
(3)解:存在,理由如下:
若,如图2,则轴,
∴,且在直线上,
∴,
解得,
∴;
若,如图3,则,
∴,
整理,得,
解得,(不符合题意,舍去);
∴,;
若,则,
∴,
整理,得,
解得,
此时不存在以,,为顶点的三角形,
∴舍去.
综上所述,点的坐标为或.
【点睛】此题重点考查二次函数的图象和性质、勾股定理、用待定系数法求函数解析式、二次根式的化简等知识,解第(3)题时应分类讨论并进行必要的检验,求出所有符合条件的点的坐标.
7.(1)A(-4,0),B(1,0),C(0,3),对称轴为直线
(2)M(1,5),N(4,1)
(3)当P的坐标为(1,0)或时,的值最大,此时最大值为
【分析】(1)提取二次项系数后分解因式,可以得出抛物线与x轴交点,令x=0代入可以得到与y轴的交点,把解析式配方后可得对称轴;
(2)根据题意作出几何图形,通过旋转性质以及通过AAS求证△OBC≌△QNB即可分别求出M、N的坐标;
(3)分析题意可得出,当P,N,B在同一直线上时,|NP-BP|的值最大,联立直线BN解析式以及抛物线解析式即可求出P的坐标.
【详解】(1)解:∵,
令x=0,则y=3,
令y=0,则,
解得x=-4或1,
∴A(-4,0),B(1,0),C(0,3),
∵,
∴对称轴为直线x=-;
(2)解:如图所示:
过N作NQ⊥x轴于点Q,
由旋转性质得MB⊥x轴,∠CBN=90°,BM=AB=5,BN=BC,
∴M(1,5),∠OBC+∠QBN=90°,
∵∠OBC+∠BCO=90°,
∴∠BCO=∠QBN,
又∵∠BOC=∠NQB=90°,BN=BC,
∴△OBC≌△QNB(AAS),
∴BQ=OC=3,NQ=OB=1,
∴OQ=1+3=4,
∴N(4,1);
(3)解:设直线NB的解析式为y=kx+b.
∵B(1,0)、N(4,1)在直线NB上,
∴,
解得:,
∴直线NB的解析式为:y=x-,
当点P,N,B在同一直线上时|NP-BP|=NB=,
当点P,N,B不在同一条直线上时|NP-BP|<NB,
∴当P,N,B在同一直线上时,|NP-BP|的值最大,
即点P为直线NB与抛物线的交点.
解方程组:,
解得:或,
∴当P的坐标为(1,0)或时,|NP-BP|的值最大,此时最大值为.
【点睛】本题属于二次函数综合题,考查待定系数法,旋转性质,全等三角形的判定与性质等知识,本题的关键是数形相结合,以及正确讨论出当P,N,B在同一直线上时,|NP-BP|的值最大是解题的关键.
8.(1)
(2)当时,△ACP面积的最大值为,此时点;
(3)点F的坐标为(﹣5,12)或(3,12)或(﹣1,﹣4)
【分析】(1)利用抛物线的解析式令时,求得点的坐标,再利用OA=OC,求得点的坐标,代入抛物线的解析式即可求解;
(2)过点P作轴交AC于点H,利用即可求解;
(3)分AB是边、AB是对角线两种情况,利用图形平移的性质和中点公式,即可求解.
【详解】(1)解:∵抛物线的解析式为,
∴当时,,
∴(0,-3)
故OC=3=OA,
∴A(﹣3,0),
将点A的坐标代入抛物线表达式得:9a﹣6a﹣3=0,解得a=1,
故抛物线的表达式为;
(2)设直线AC的表达式为,
∵直线AC过点(0,-3),A(﹣3,0),
∴,解得
∴直线AC的表达式为y=﹣x﹣3,
过点P作轴交AC于点H,
设点P(x,),则点H(x,﹣x﹣3),
∴,
则
,
∵<0,故△ACP面积有最大值,当时,△ACP面积的最大值为,
∴当时,
此时点P(,);
(3)对于,令y=0,
即,
解得x=﹣3或1,
故点B(1,0),
∴抛物线的对称轴为直线为x=﹣1,
设点F(m,n),即n=m2+2m﹣3①,点E(﹣1,t),
①当AB是边时,
点A向右平移4个单位得到点B,同样点F(E)向右平移4个单位得到点E(F),
即m±4=﹣1②,
联立①②并解得或,
故点F的坐标为(﹣5,12)或(3,12);
②当AB是对角线时,A(﹣3,0),B(1,0),
由中点公式得:③,
联立①③并解得,
故点F的坐标为(﹣1,﹣4);
综上,点F的坐标为(﹣5,12)或(3,12)或(﹣1,﹣4).
【点睛】本题考查的是二次函数综合运用,涉及到一次函数的性质、平行四边形的性质、中点坐标公式的运用、图形的平移等,其中(3),要注意分类求解,避免遗漏.
9.(1)
(2)P(4,21),(﹣4,5)
(3)
【分析】(1)根据OA=OC,可求c;再依据对称轴是直线x=﹣1,点A的坐标为(﹣3,0),可求a、b,即得求抛物线解析式.
(2)可求△BOC的面积,根据,可求P点坐标.
(3)求出直线AC解析式,设点Q(m,﹣m﹣3)(﹣3≤m≤0),则点D,根据二次函数的最值求法,可求QD的最大值.
【详解】(1)令x=0,则y=c,
∴OC=﹣c,
∵OA=OC,
∴3=﹣c,即c=﹣3.
∵对称轴是直线x=﹣1,点A的坐标为(﹣3,0),
根据题意得:,
解之:.
∴抛物线解析式.
(2)当x=0时,y=﹣3,
∴点C(0,﹣3),即OC=3,
∵A,B关于对称轴对称,
∴B(1,0),即OB=1,
∴,
设,
∴=×3×|x|,
∵=,
∴,
∴x=±4,
∴P(4,21),(﹣4,5).
(3)∵点A(﹣3,0),点C(0,﹣3),
∴直线AC解析式y=﹣x﹣3,
∴设点Q(m,﹣m﹣3)(﹣3≤m≤0),
则点,
∴,
∴当m=﹣时,QD的最大值为 .
【点睛】本题考查了二次函数的综合题,待定系数法求解析式,二次函数的最值问题,利用数形结合思想解决问题是本题的关键
10.(1)
(2)存在,或(3,4)
(3)存在,
【分析】(1)待定系数法求解析式即可求解;
(2)待定系数法求得直线AB的解析式为,过点P作PM⊥x轴,垂足为M,PM交AB于点N.过点B作BE⊥PM,垂足为E.可得,设,则.由,解方程求得的值,进而即可求解;
(3)由已知条件可得,进而可得,过点分别作轴的垂线,垂足分别,交于点,过作的平行线,交于点,可得,设,,则,根据可得,根据,根据二次函数的性质即可求的最大值.
【详解】(1)解:(1)将A(4,0),B(1,4)代入,
得,
解得.
所以抛物线的解析式为.
(2)设直线AB的解析式为,
将A(4,0),B(1,4)代入,
得,
解得.
所以直线AB的解析式为.
过点P作PM⊥x轴,垂足为M,PM交AB于点N.
过点B作BE⊥PM,垂足为E.
所以
.
因为A(4,0),B(1,4),所以.
因为△OAB的面积是△PAB面积的2倍,
所以,.
设,则.
所以,
即,
解得,.
所以点P的坐标为或(3,4).
(3)
记△CDP,△CPB,△CBO的面积分别为,,.则
如图,过点分别作轴的垂线,垂足分别,交于点,过作的平行线,交于点
,
,
设
直线AB的解析式为.
设,则
整理得
时,取得最大值,最大值为
【点睛】本题考查了二次函数综合,待定系数法求解析式,面积问题,相似三角形的性质与判定,第三问中转化为线段的比是解题的关键.
11.(1),C(0,-3)
(2)M(4,5)或M(2,-3)
(3)有,P点的坐标为(,-)
【分析】(1)把点的坐标代入解析式,转化为方程组,确定a,b的值即可.
(2)分点M在第一象限和第四象限两种情况根据45度角的特征列方程求解即可.
(3)根据垂直及对顶角相等易证△FPE∽△OBC,根据相似三角形的性质将题转化为与△OBC的周长有关的比例式;设直线BC的解析式为y=px+q,根据待定系数法求出直线BC的解析式,设P(n,),则E(n,n-3),列出关于n的二次函数式,根据二次函数最值即可得出答案.
【详解】(1)由题意得
,
解得,
∴抛物线的解析式为,
∴点C(0,-3).
(2)①当M点在第一象限时,
设M(m,),
过M点作MN⊥x轴,
∵∠MAB=45°,MN=NA,
∴m+1=,
解方程得:m=4或m=-1,
m=-1不合题意,舍去.
故m=4 ,
∴M(4,5);
当M点在第四象限时,同理可得:
m+1=-()
解方程得:m=2或m=-1,
m=-1不合题意,舍去.
故m=2,
∴M(2,-3),
综上M(4,5)或M(2,-3).
(3)△PEF的周长有最大值.理由如下:
∵PD⊥DB,
∴∠EBD=90°-∠DEB,
∵PF⊥BC,
∴∠FPE=90°-∠FEP,
∵∠DEB=∠FEP,
∴∠EBD=∠FPE,
又∵∠EFP=∠BOC=90°,
∴△FPE∽△OBC,
∴△PEF的周长:△OBC的周长=PE:BC,
∵OB=OC=3,
∴BC=,
∴△PEF的周长为z,△OBC的周长=,
∵直线BC过B(3,0)和C(0,-3),
设直线BC的解析式为y=px+q,
∴,
解得,
∴直线BC的解析式为y=x-3,
设P(n,),则E(n,n-3)
PE=n-3-()=,
∴z:(6+3)=():3,
z=-(+1) +3(+1)n,
∵-(+1)<0,
∴z有最大值,此时n=,
当n=时,=-,
故P点的坐标为(,-).
【点睛】本题考查了待定系数法确定函数的解析式,解方程,三角形相似的判断和性质,二次函数的最值,熟练掌握二次函数的最值是解题的关键.
12.(1)
(2)S的最大值为4
(3)或或.
【分析】(1)先假设出函数解析式,利用待定系数法求解函数解析式即可;
(2)设出M点的坐标,利用,即可进行解答;
(3)由,则,是平行四边形的边,根据平行四边形的对边相等,列出方程求解即可.
【详解】(1)解:设此抛物线的函数解析式为:,
将,,三点代入函数解析式得:
,
解得,
所以此函数解析式为:;
(2)解:连接 ,
∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为,
∴
,
∵,
当时,S有最大值为:.
(3)解:设,
根据平行四边形的性质知,且,则,为平行四边形的边,
∴Q的横坐标等于P的横坐标,
又∵直线的解析式为,
则,
由,得,
整理得:
所以或
解得或或(不符合题意,舍去),
∵,
∴不可能是对角线
∴由此可得:或或.
【点睛】本题考查的是二次函数综合运用,涉及到平行四边形的性质、面积的计算等,有一定的综合性,熟练的利用二次函数的性质与平行四边形的性质解题是关键.
13.(1)抛物线的关系式为;(2),当时,取得最大值;(3)点的坐标为或或或.
【分析】(1)将点A(,),B(,)分别代入抛物线的关系式中,即可求解;
(2)先求得的周长,证得,,利用相似三角形的性质得到二次函数的关系式,再利用二次函数的性质即可求解;
(3)分三种情形分别求解①当∠BCP=90°,②当∠CBP=90°,③当∠BPC=90°时,根据勾股定理列出方程即可.
【详解】(1)将点,分别代入抛物线的关系式中,得
解得,
∴抛物线的关系式为;
(2)令 ,则,
∴点C的坐标为(,),
∵点B的坐标为(,),
∴OB=3,OC=4,BC=,
∴的周长为,
设直线的关系式为,
把点B的坐标为(,)代入得:,
∴直线的关系式为,
∵点的横坐标为,
∴,,
∵轴,
∴,
∴,
∵,,
∴,
∴,
∴,,
∴,,
即,
∵,
∴当时,取得最大值;
(3)抛物线的关系式为,
∴抛物线的对称轴为:,
∴设点P的坐标为(1,m),
∴,
,
,
①当∠BCP=90°时,
∵,即,
解得:,
∴点P的坐标为(1,);
②当∠CBP=90°时,
∵,即,
解得:,
∴点P的坐标为(1,);
③当∠BPC=90°时,
∵,即,
解得:或
∴点P的坐标为(1,)或(1,);
综上,点的坐标为(1,)或(1,)或(1,)或(1,).
【点睛】本题是二次函数综合题,考查了待定系数法求函数解析式,二次函数的性质,相似三角形的判定和性质,勾股定理的应用等知识,解题的关键是学会构建二次函数解决最值问题,学会用分类讨论的思想思考问题,属于中考压轴题.
14.(1)y=x2-4x+3;(2)点P在运动的过程中,线段PD长度的最大值为;(3)能,点P的坐标为:(1,0)或(2,-1).
【分析】(1)把点A、B的坐标代入抛物线解析式,解方程组得到b、c的值,即可得解;
(2)求出点C的坐标,再利用待定系数法求出直线AC的解析式,再根据抛物线解析式设出点P的坐标,然后表示出PD的长度,再根据二次函数的最值问题解答;
(3)分情况讨论①∠APD是直角时,点P与点B重合,②求出抛物线顶点坐标,然后判断出点P为在抛物线顶点时,∠PAD是直角,分别写出点P的坐标即可;
【详解】(1)把点A(3,0)和点B(1,0)代入抛物线y=x2+bx+c,
得:
解得
∴y=x2-4x+3.
(2)把x=0代入y=x2-4x+3,得y=3.
∴C(0,3).
又∵A(3,0),
设直线AC的解析式为:y=kx+m,
把点A,C的坐标代入得:
∴直线AC的解析式为:y=-x+3.
PD=-x+3- (x2-4x+3)=-x2+3x=+.
∵0
即点P在运动的过程中,线段PD长度的最大值为.
(3)①∠APD是直角时,点P与点B重合,
此时,点P(1,0),
②∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的顶点坐标为(2,﹣1),
∵A(3,0),
∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,
此时,点P(2,﹣1),
综上所述,点P(1,0)或(2,﹣1)时,△APD能构成直角三角形;
【点睛】本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,二次函数的最值问题,二次函数的对称性以及顶点坐标的求解,直角三角形存在性问题时需要分类讨论.
15.(1);(2)在,理由见解析;(3)s=,时,最大,点的坐标为.
【分析】(1)已知了抛物线上A、B点的坐标以及抛物线的对称轴方程,可用待定系数法求出抛物线的解析式.(2)首先求出AB的长,将A、B的坐标向右平移AB个单位,即可得出C、D的坐标,再代入抛物线的解析式中进行验证即可.(3)根据C、D的坐标,易求得直线CD的解析式;那么线段MN的长实际是直线BC与抛物线的函数值的差,可将x=t代入两个函数的解析式中,得出的两函数值的差即为l的表达式,由此可求出l、t的函数关系式,根据所得函数的性质即可求出l取最大值时,点M的坐标.
【详解】(1)∵的顶点在直线上,
∴可设所求抛物线对应的函数关系式为,
∴点在此抛物线上,
∴,
∴,
∴所求函数关系式为:;
(2)在中,,,
∴,
∵四边形是菱形,
∴,
∵两点的坐标分别是、,
∴两点的坐标分别是、;
当时,;
当时,;
∴点和点在所求抛物线上;
(3)设直线对应的函数关系式为,
则,
解得:;
∴.
∵轴,点点的横坐标为,
∴点的横坐标也为;
则,,
∴
,
∵,
∴当时,最大,此时.
此时点的坐标为.
【点睛】本题考查待定系数法求一次函数、二次函数解析式、菱形的性质、图象的平移变换,等知识.熟练掌握待定系数法是解题的关键.
16.(1)所求抛物线的解析式是;
(2)点的坐标为,或;
(3)如当时,有最大值.
【分析】(1)因为抛物线的对称轴为,可得h值;点坐标为在抛物线上,代入抛物线的解析式,即可解答;
(2)先由二次函数的解析式为,得到点坐标,然后设点坐标为,根据列出关于的方程,解方程求出的值,进而得到点的坐标;
(3)先运用待定系数法求出直线的解析式为,再设点坐标为,则点坐标为,然后用含的代数式表示,根据二次函数的性质即可求出线段长度的最大值.
【详解】(1)由题意对称轴为直线,
设抛物线解析式为,把点代入得,
.
∴所求抛物线的解析式是.
(2)如图1.
,当时,.所以点,.
令,解得,或.点,.
设点.
此时.
.
由得.
解得或.
所以或.
所以点的坐标为,或.
(3)如图2.
设直线的解析式为:.
把,代入得,解得.
所以直线AC的解析式为.
设点,点.
所以.
所以当时,有最大值.
【点睛】此题考查了待定系数法求二次函数、一次函数的解析式,二次函数的性质以及三角形面积、线段长度问题.此题难度适中,解题的关键是运用方程思想与数形结合思想.
17.(1) (﹣1,4);(2)见解析;(3) 2.25.
【分析】(1)根据二次函数的解析式直接写出即可;
(2)先根据二次函数求出A、C的坐标,再用待定系数法确定直线AC的关系式,再求出
点D1,把它代入直线判断是否再直线上;
(3)设点E(x,﹣x2﹣2x+3),F(x,x+3),则EF=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+1.5)2+2.25, 则可知x=-1.5时,EF的最大值2.25.
【详解】解:(1)∵y=﹣(x+1)2+4,
∴抛物线顶点D的坐标是(﹣1,4).
故答案为(﹣1,4);
(2)点D1在直线AC上,理由如下:
∵抛物线y=﹣(x+1)2+4与x轴交于点A、B,与y轴交于点C,
∴当y=0时,﹣(x+1)2+4=0,解得x=1或﹣3,A(﹣3,0),B(1,0),
当x=0时,y=﹣1+4=3,C(0,3).
设直线AC的解析式为y=kx+b,
由题意得,解得,
∴直线AC的解析式为y=x+3.
∵点D1是点D关于y轴的对称点,D(﹣1,4).
∴D1(1,4),
∵x=1时,y=1+3=4,
∴点D1在直线AC上;
(3)设点E(x,﹣x2﹣2x+3),则F(x,x+3),
∵EF=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+1.5)2+2.25,
∴线段EF的最大值是2.25.
【点睛】此题主要考查二次函数的图像,根据题意求出与坐标轴的交点是解题的关键.
18.(1)y=﹣x2﹣2x+3;y=﹣x+1;(2)当x=﹣时,△APC的面积取最大值,最大值为,此时点P的坐标为(﹣,);(3)在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为3.
【分析】(1)根据点A,C的坐标,利用待定系数法即可求出抛物线及直线AC的函数关系式;(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,设点P的坐标为(x,﹣x2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),进而可得出PF的值,由点C的坐标可得出点Q的坐标,进而可得出AQ的值,利用三角形的面积公式可得出S△APC=﹣x2﹣x+3,再利用二次函数的性质,即可解决最值问题;(3)利用二次函数图象上点的坐标特征可得出点N的坐标,利用配方法可找出抛物线的对称轴,由点C,N的坐标可得出点C,N关于抛物线的对称轴对称,令直线AC与抛物线的对称轴的交点为点M,则此时△ANM周长取最小值,再利用一次函数图象上点的坐标特征求出点M的坐标,以及利用两点间的距离公式结合三角形的周长公式求出△ANM周长的最小值即可得出结论.
【详解】(1)将A(1,0),C(﹣2,3)代入y=﹣x2+bx+c,得:
,解得:,
∴抛物线的函数关系式为y=﹣x2﹣2x+3;
设直线AC的函数关系式为y=mx+n(m≠0),
将A(1,0),C(﹣2,3)代入y=mx+n,得:
,解得:,
∴直线AC的函数关系式为y=﹣x+1.
(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,如图1所示.
设点P的坐标为(x,﹣x2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),
∴PE=﹣x2﹣2x+3,EF=﹣x+1,EF=PE﹣EF=﹣x2﹣2x+3﹣(﹣x+1)=﹣x2﹣x+2.
∵点C的坐标为(﹣2,3),
∴点Q的坐标为(﹣2,0),
∴AQ=1﹣(﹣2)=3,
∴S△APC=AQ PF=﹣x2﹣x+3=﹣(x+)2+ .
∵﹣<0,
∴当x=﹣时,△APC的面积取最大值,最大值为,此时点P的坐标为(﹣, ).
(3)当x=0时,y=﹣x2﹣2x+3=3,
∴点N的坐标为(0,3).
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的对称轴为直线x=﹣1.
∵点C的坐标为(﹣2,3),
∴点C,N关于抛物线的对称轴对称.
令直线AC与抛物线的对称轴的交点为点M,如图2所示.
∵点C,N关于抛物线的对称轴对称,
∴MN=CM,
∴AM+MN=AM+MC=AC,
∴此时△ANM周长取最小值.
当x=﹣1时,y=﹣x+1=2,
∴此时点M的坐标为(﹣1,2).
∵点A的坐标为(1,0),点C的坐标为(﹣2,3),点N的坐标为(0,3),
∴AC= =3,AN= =,
∴C△ANM=AM+MN+AN=AC+AN=3+.
∴在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为3+.
【点睛】本题考查待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图象上点的坐标特征、一次函数图象上点的坐标特征、二次函数的性质、三角形的面积以及周长,解题的关键是:(1)根据点的坐标,利用待定系数法求出抛物线及直线AC的函数关系式;(2)利用三角形的面积公式找出S△APC=﹣x2﹣x+3的最值;(3)利用二次函数图象的对称性结合两点之间线段最短找出点M的位置.
同课章节目录
