2024年九年级中考数学专项练习:一次函数背景下的存在性问题(无答案)
文档属性
| 名称 | 2024年九年级中考数学专项练习:一次函数背景下的存在性问题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 548.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 18:34:54 | ||
图片预览



文档简介
2023-2024学年九年级+中考数学专项练习:一次函数背景下的存在性问题
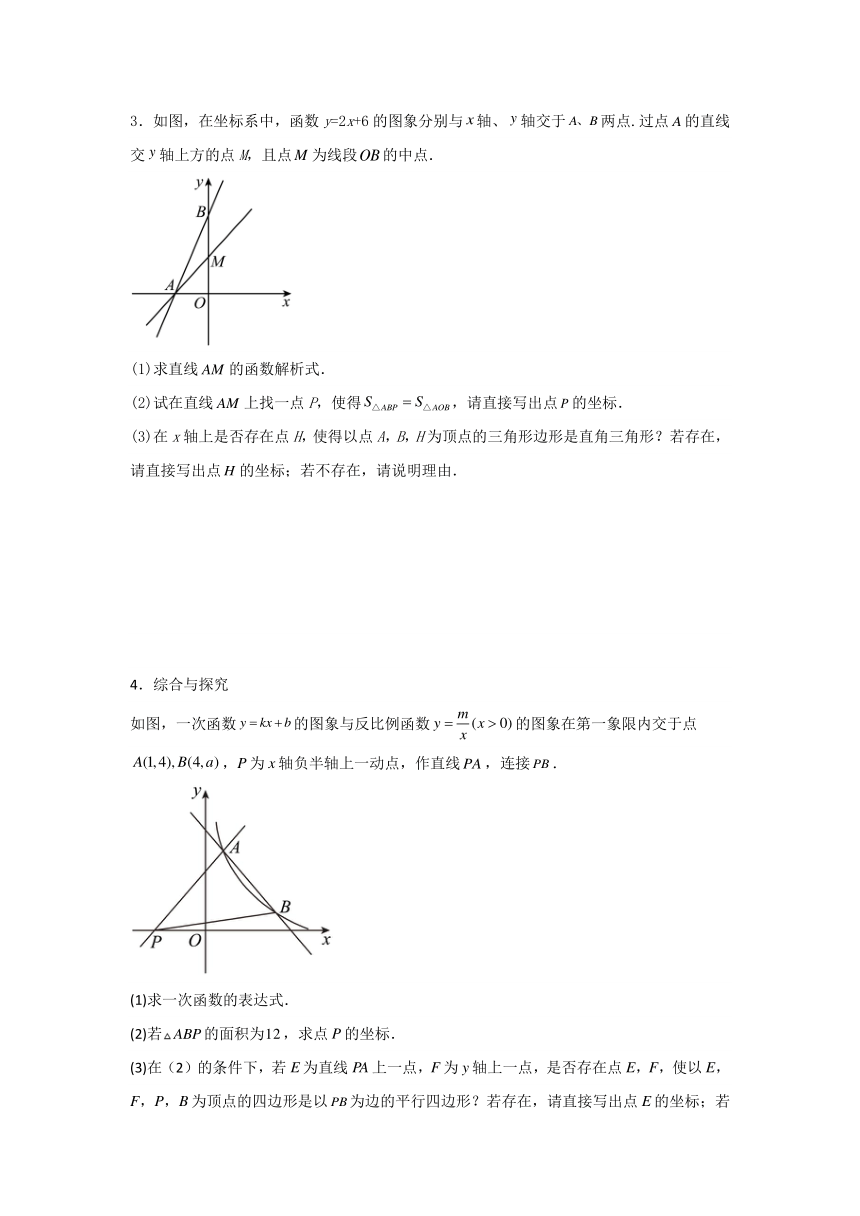
1. 如图,在△ABC中,AB=AC,∠BAC=120°,直角三角板含30°角的顶点P在边BC上移动(点P不与B、C重合),一直角边始终经过点A,斜边与腰AC交于点D,若△APB为等腰三角形,则∠PAB的度数= .
2.如图,在平面直角坐标系xOy中,直线AB:y=kx+3k(k≠0)交x轴于点B,交y轴于点A,AB=3.
(1)求点A的坐标;
(2)点C为x轴正半轴上一点,∠BAO=∠ACO,点M为线段AC上一动点,设M的纵坐标为a(a≠0),请用含a的代数式表示点M到y轴的距离d;
(3)在(2)的条件下,过点M作MN∥AB交x轴于点N,连接BM,AN,当△ABM为等腰三角形时,求△AMN的面积.
3.如图,在坐标系中,函数y=2x+6的图象分别与轴、轴交于两点.过点的直线交轴上方的点M,且点为线段的中点.
(1)求直线的函数解析式.
(2)试在直线上找一点P,使得,请直接写出点的坐标.
(3)在x轴上是否存在点H,使得以点A,B,H为顶点的三角形边形是直角三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
4.综合与探究
如图,一次函数的图象与反比例函数的图象在第一象限内交于点,P为x轴负半轴上一动点,作直线,连接.
(1)求一次函数的表达式.
(2)若的面积为,求点P的坐标.
(3)在(2)的条件下,若E为直线PA上一点,F为y轴上一点,是否存在点E,F,使以E,F,P,B为顶点的四边形是以为边的平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
5.如图,直线l1:y1=-x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l 1上一点,另一直线l2:y2=x+b过点P.
(1)求点P坐标和b的值;
(2)若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动至 A,设点Q的运动时间为t秒.
①请写出当点Q在运动过程中,APQ的面积S与t的函数关系式;
②是否存在t的值,使APQ面积为APC的一半?若存在,请求出t的值;若不存在,请说明理由.
③是否存在t的值,使APQ为以AQ为底的等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
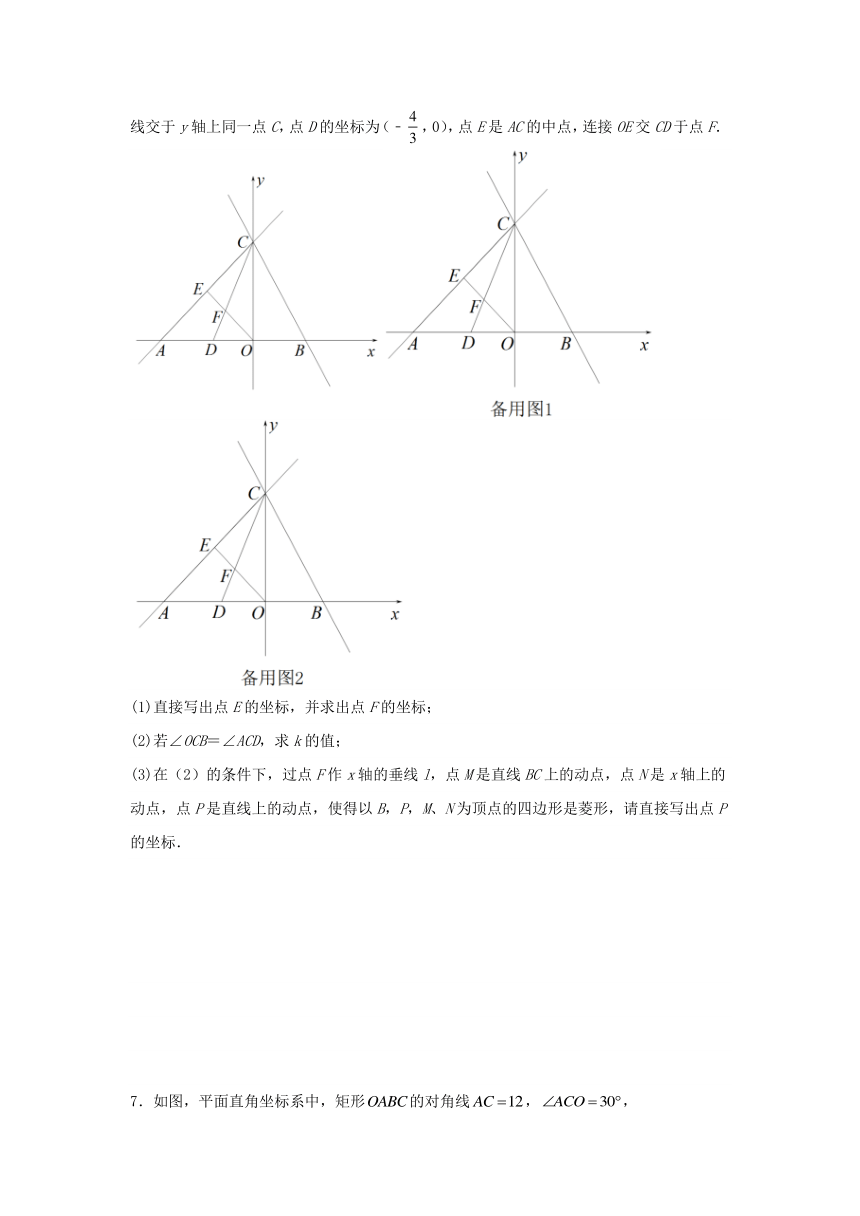
6.如图,在平面直角坐标系xOy中,直线y=x+4与y=kx+4分别交x轴于点A、B,两直线交于y轴上同一点C,点D的坐标为(﹣,0),点E是AC的中点,连接OE交CD于点F.
(1)直接写出点E的坐标,并求出点F的坐标;
(2)若∠OCB=∠ACD,求k的值;
(3)在(2)的条件下,过点F作x轴的垂线l,点M是直线BC上的动点,点N是x轴上的动点,点P是直线上的动点,使得以B,P,M、N为顶点的四边形是菱形,请直接写出点P的坐标.
7.如图,平面直角坐标系中,矩形的对角线,,
(1)求B点的坐标;
(2)把矩形沿直线对折使点C落在点A处,与相交于点F,求四边形的周长;
(3)若点M在坐标轴上,平面内是否存在点N,使以O、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
8、已知,如图,在第一象限中,点A的坐标是(3,6),射线OM的解析式为y=x,作线段AC⊥x轴于点C,点B在射线OM上,且OB的长度为3.
(1)求△AOB的面积;
(2)试判断△AOB的形状,并说明理由;
(3)直线AB交坐标轴于E、F两点,若点P在线段EF上,点Q在线段OF上,且△FPQ与△AOC全等,求点Q的坐标.
9.一次函数y=kx+b的图象与x轴、y轴分别交于点A(a,0),点B(0,b).过B点作垂直于直线AB的直线交x轴于点C,过A点的直线交线段OB于点D,交直线BC于点E.其中实数a、b满足b2+8b+16=0.
(1)求直线AB解析式;
(2)如图1,当BE=DE时,求E点坐标;
(3)如图2,当BD=DE时,F为直线AC上一点,且位于E点右侧,过点F作平行于y轴的直线交直线AD于点G,点H为直线AB上的动点,当△FGH为等腰直角三角形时,求点H坐标.
10.如图1,平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
(1)求点C的坐标及直线AB的表达式;
(2)如图2,在x轴上有一点E,过点E作直线⊥x轴,交直线y=2x于点F,交直线y=kx+b于点G,若GF的长为3.求点E的坐标;
(3)在y轴上是否存在一点F,使以O、C、F为顶点的三角形是等腰三角形,若存在,直接写出点F的坐标;若不存在,说明理由.
11.如图1,在平面直角坐标系中,直线交x轴于点C,交y轴于点D,,,点P是直线上一动点,连接,.
(1)求直线的表达式;
(2)求的最小值;
(3)如图2,将三角形沿翻折得到,当点落在坐标轴上时,请直接写出直线的表达式.
12.如图1,在平面直角坐标系中,直线:与x轴交于点,与y轴交于点.直线:与直线交于点C.
(1)求直线的解析式.
(2)如图2,点P是射线上的任意一点,过点P作轴且与交于点D,连接.当时,求的面积.
(3)如图3,在(2)的条件下,将先向右平移2个单位,再向上平移4个单位,点P的对应点为点F.在x轴上确定一点G,使得以点A,F,G为顶点的三角形是等腰三角形,直接写出所有符合条件的点G的坐标.
13、如图,已知一次函数y=3x+3与y轴交于A,与x轴交于点B,直线AC与正半轴交于点C,且AC=BC.
(1)求直线AC的解析式.
(2)点D为线段AC上一点,点E为线段CD的中点,过点E作x轴的平行线交直线AB于点F,连接DF并延长交x轴于点G,求证;AD=BG.
(3)在(2)的条件下,若∠AFD=2∠BAO,求点D坐标.
14.如图 1,在平面直角坐标系中,直线l1:yx5与x轴,y轴分别交于A.B两点.直线l2:y4xb与l1交于点 D(-3,8)且与x轴,y轴分别交于C、E.
(1)求出点A坐标,直线l2的解析式;
(2)如图2,点P为线段AD上一点(不含端点),连接CP,一动点Q从C出发,沿线段CP 以每秒1个单位的速度运动到点P,再沿着线段PD以每秒个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
(3)如图3,平面直角坐标系中有一点G(m,2),使得SCEGSCEB,求点G的坐标.
15.如图1,直线与坐标轴分别交于两点,过点的直线交轴于点.
(1)求直线的解析式并判定的形状;
(2)如图2,若点,是直线上的一动点,连接,当的值最小时,求点的坐标,并求出这个最小值;
(3)如图3,将直线向上平移个单位,与坐标轴交于点,分别以为腰,点为直角顶点分别在第一、二象限作等腰直角和等腰直角,连接交轴于点,求的长度.
8、【模型建立】
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CA=CB,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△CDA≌△BEC.
【模型运用】
(2)如图2,直线l1:y=x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转90°至直线l2,求直线l2的函数表达式.
【模型迁移】
如图3,直线l经过坐标原点O,且与x轴正半轴的夹角为30°,点A在直线l上,点P为x轴上一动点,连接AP,将线段AP绕点P顺时针旋转30°得到BP,过点B的直线BC交x轴于点C,∠OCB=30°,点B到x轴的距离为2,求点P的坐标.
1. 如图,在△ABC中,AB=AC,∠BAC=120°,直角三角板含30°角的顶点P在边BC上移动(点P不与B、C重合),一直角边始终经过点A,斜边与腰AC交于点D,若△APB为等腰三角形,则∠PAB的度数= .
2.如图,在平面直角坐标系xOy中,直线AB:y=kx+3k(k≠0)交x轴于点B,交y轴于点A,AB=3.
(1)求点A的坐标;
(2)点C为x轴正半轴上一点,∠BAO=∠ACO,点M为线段AC上一动点,设M的纵坐标为a(a≠0),请用含a的代数式表示点M到y轴的距离d;
(3)在(2)的条件下,过点M作MN∥AB交x轴于点N,连接BM,AN,当△ABM为等腰三角形时,求△AMN的面积.
3.如图,在坐标系中,函数y=2x+6的图象分别与轴、轴交于两点.过点的直线交轴上方的点M,且点为线段的中点.
(1)求直线的函数解析式.
(2)试在直线上找一点P,使得,请直接写出点的坐标.
(3)在x轴上是否存在点H,使得以点A,B,H为顶点的三角形边形是直角三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
4.综合与探究
如图,一次函数的图象与反比例函数的图象在第一象限内交于点,P为x轴负半轴上一动点,作直线,连接.
(1)求一次函数的表达式.
(2)若的面积为,求点P的坐标.
(3)在(2)的条件下,若E为直线PA上一点,F为y轴上一点,是否存在点E,F,使以E,F,P,B为顶点的四边形是以为边的平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
5.如图,直线l1:y1=-x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l 1上一点,另一直线l2:y2=x+b过点P.
(1)求点P坐标和b的值;
(2)若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动至 A,设点Q的运动时间为t秒.
①请写出当点Q在运动过程中,APQ的面积S与t的函数关系式;
②是否存在t的值,使APQ面积为APC的一半?若存在,请求出t的值;若不存在,请说明理由.
③是否存在t的值,使APQ为以AQ为底的等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
6.如图,在平面直角坐标系xOy中,直线y=x+4与y=kx+4分别交x轴于点A、B,两直线交于y轴上同一点C,点D的坐标为(﹣,0),点E是AC的中点,连接OE交CD于点F.
(1)直接写出点E的坐标,并求出点F的坐标;
(2)若∠OCB=∠ACD,求k的值;
(3)在(2)的条件下,过点F作x轴的垂线l,点M是直线BC上的动点,点N是x轴上的动点,点P是直线上的动点,使得以B,P,M、N为顶点的四边形是菱形,请直接写出点P的坐标.
7.如图,平面直角坐标系中,矩形的对角线,,
(1)求B点的坐标;
(2)把矩形沿直线对折使点C落在点A处,与相交于点F,求四边形的周长;
(3)若点M在坐标轴上,平面内是否存在点N,使以O、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
8、已知,如图,在第一象限中,点A的坐标是(3,6),射线OM的解析式为y=x,作线段AC⊥x轴于点C,点B在射线OM上,且OB的长度为3.
(1)求△AOB的面积;
(2)试判断△AOB的形状,并说明理由;
(3)直线AB交坐标轴于E、F两点,若点P在线段EF上,点Q在线段OF上,且△FPQ与△AOC全等,求点Q的坐标.
9.一次函数y=kx+b的图象与x轴、y轴分别交于点A(a,0),点B(0,b).过B点作垂直于直线AB的直线交x轴于点C,过A点的直线交线段OB于点D,交直线BC于点E.其中实数a、b满足b2+8b+16=0.
(1)求直线AB解析式;
(2)如图1,当BE=DE时,求E点坐标;
(3)如图2,当BD=DE时,F为直线AC上一点,且位于E点右侧,过点F作平行于y轴的直线交直线AD于点G,点H为直线AB上的动点,当△FGH为等腰直角三角形时,求点H坐标.
10.如图1,平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
(1)求点C的坐标及直线AB的表达式;
(2)如图2,在x轴上有一点E,过点E作直线⊥x轴,交直线y=2x于点F,交直线y=kx+b于点G,若GF的长为3.求点E的坐标;
(3)在y轴上是否存在一点F,使以O、C、F为顶点的三角形是等腰三角形,若存在,直接写出点F的坐标;若不存在,说明理由.
11.如图1,在平面直角坐标系中,直线交x轴于点C,交y轴于点D,,,点P是直线上一动点,连接,.
(1)求直线的表达式;
(2)求的最小值;
(3)如图2,将三角形沿翻折得到,当点落在坐标轴上时,请直接写出直线的表达式.
12.如图1,在平面直角坐标系中,直线:与x轴交于点,与y轴交于点.直线:与直线交于点C.
(1)求直线的解析式.
(2)如图2,点P是射线上的任意一点,过点P作轴且与交于点D,连接.当时,求的面积.
(3)如图3,在(2)的条件下,将先向右平移2个单位,再向上平移4个单位,点P的对应点为点F.在x轴上确定一点G,使得以点A,F,G为顶点的三角形是等腰三角形,直接写出所有符合条件的点G的坐标.
13、如图,已知一次函数y=3x+3与y轴交于A,与x轴交于点B,直线AC与正半轴交于点C,且AC=BC.
(1)求直线AC的解析式.
(2)点D为线段AC上一点,点E为线段CD的中点,过点E作x轴的平行线交直线AB于点F,连接DF并延长交x轴于点G,求证;AD=BG.
(3)在(2)的条件下,若∠AFD=2∠BAO,求点D坐标.
14.如图 1,在平面直角坐标系中,直线l1:yx5与x轴,y轴分别交于A.B两点.直线l2:y4xb与l1交于点 D(-3,8)且与x轴,y轴分别交于C、E.
(1)求出点A坐标,直线l2的解析式;
(2)如图2,点P为线段AD上一点(不含端点),连接CP,一动点Q从C出发,沿线段CP 以每秒1个单位的速度运动到点P,再沿着线段PD以每秒个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
(3)如图3,平面直角坐标系中有一点G(m,2),使得SCEGSCEB,求点G的坐标.
15.如图1,直线与坐标轴分别交于两点,过点的直线交轴于点.
(1)求直线的解析式并判定的形状;
(2)如图2,若点,是直线上的一动点,连接,当的值最小时,求点的坐标,并求出这个最小值;
(3)如图3,将直线向上平移个单位,与坐标轴交于点,分别以为腰,点为直角顶点分别在第一、二象限作等腰直角和等腰直角,连接交轴于点,求的长度.
8、【模型建立】
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CA=CB,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△CDA≌△BEC.
【模型运用】
(2)如图2,直线l1:y=x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转90°至直线l2,求直线l2的函数表达式.
【模型迁移】
如图3,直线l经过坐标原点O,且与x轴正半轴的夹角为30°,点A在直线l上,点P为x轴上一动点,连接AP,将线段AP绕点P顺时针旋转30°得到BP,过点B的直线BC交x轴于点C,∠OCB=30°,点B到x轴的距离为2,求点P的坐标.
同课章节目录
