求二次函数的解析式
图片预览




文档简介
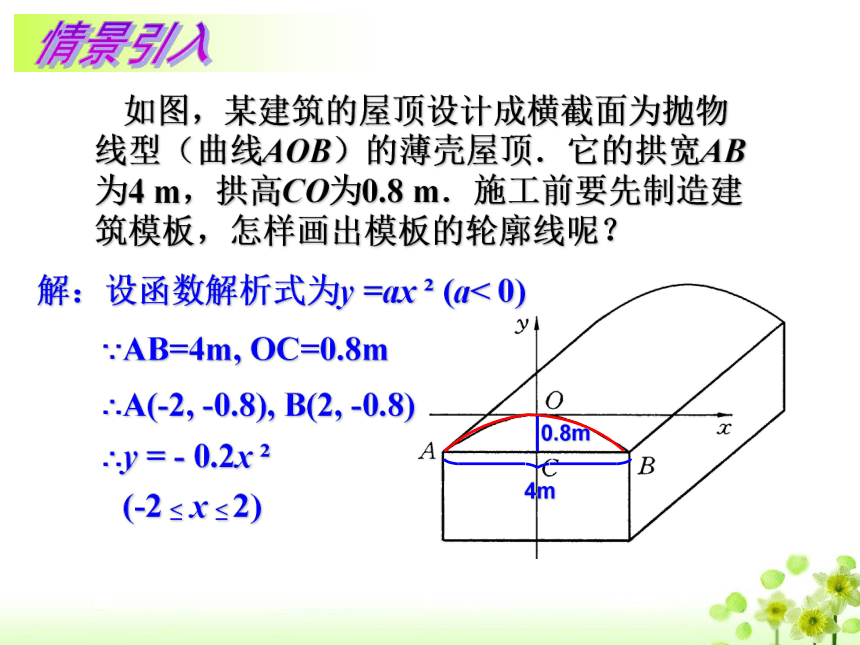
课件11张PPT。0.8m解:设函数解析式为y =ax 2 (a< 0)∵AB=4m, OC=0.8m∴A(-2, -0.8), B(2, -0.8)∴y = - 0.2x 2(-2 ≤ x ≤ 2)例1、已知抛物线经过(-1,0)、(0,-3)、(2,-3)
三点:
(1)求抛物线的解析式;
(2)写出抛物线的开口方向,对称轴和顶
点坐标.1、一般式: y =ax 2+bx +c (a≠ 0)特点:已知三点坐标.方法:将三对对应值代入,求出a、b、c的值.例2、已知一个二次函数的图象经过点(3,-4),且当x=2时,函数的最大值为-1,顶点是(-2,3),且过(-1,5),求其解析式.1、一般式: y =ax 2+bx +c (a≠ 0)特点:已知三点坐标.方法:将三对对应值代入,求出a、b、c的值.2、顶点式:y =a(x-h)2+k (a≠ 0)特点:已知顶点坐标或最大(小)值或
对称轴和另一点坐标.方法:将顶点(或最值)和另一点的坐标代入
顶点式,求出a的值.求下列二次函数解析式:(1)抛物线 y = x2-5(m+1)x+2m的对称轴是y轴.(2)抛物线y=(m-3)x2+mx+m+3的最大值是0. (3)抛物线y=ax2+bx+c与y=-x2形状相同,对称轴是直线x=3,最高点在直线 y=x+1上,求抛物线解析式.(0,0)
(2,0)
(1,-1)如图:求二次函数的关系式.求二次函数解析式:已知图象过一般三点已知顶点坐标
已知最大(小)值
已知对称轴和另一点坐标本节课你掌握了哪些知识?谢谢 再见
三点:
(1)求抛物线的解析式;
(2)写出抛物线的开口方向,对称轴和顶
点坐标.1、一般式: y =ax 2+bx +c (a≠ 0)特点:已知三点坐标.方法:将三对对应值代入,求出a、b、c的值.例2、已知一个二次函数的图象经过点(3,-4),且当x=2时,函数的最大值为-1,顶点是(-2,3),且过(-1,5),求其解析式.1、一般式: y =ax 2+bx +c (a≠ 0)特点:已知三点坐标.方法:将三对对应值代入,求出a、b、c的值.2、顶点式:y =a(x-h)2+k (a≠ 0)特点:已知顶点坐标或最大(小)值或
对称轴和另一点坐标.方法:将顶点(或最值)和另一点的坐标代入
顶点式,求出a的值.求下列二次函数解析式:(1)抛物线 y = x2-5(m+1)x+2m的对称轴是y轴.(2)抛物线y=(m-3)x2+mx+m+3的最大值是0. (3)抛物线y=ax2+bx+c与y=-x2形状相同,对称轴是直线x=3,最高点在直线 y=x+1上,求抛物线解析式.(0,0)
(2,0)
(1,-1)如图:求二次函数的关系式.求二次函数解析式:已知图象过一般三点已知顶点坐标
已知最大(小)值
已知对称轴和另一点坐标本节课你掌握了哪些知识?谢谢 再见
