人教版小学数学二年级上册4.2.3 《乘加、乘减》课件(共24张PPT)
文档属性
| 名称 | 人教版小学数学二年级上册4.2.3 《乘加、乘减》课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 20:40:15 | ||
图片预览

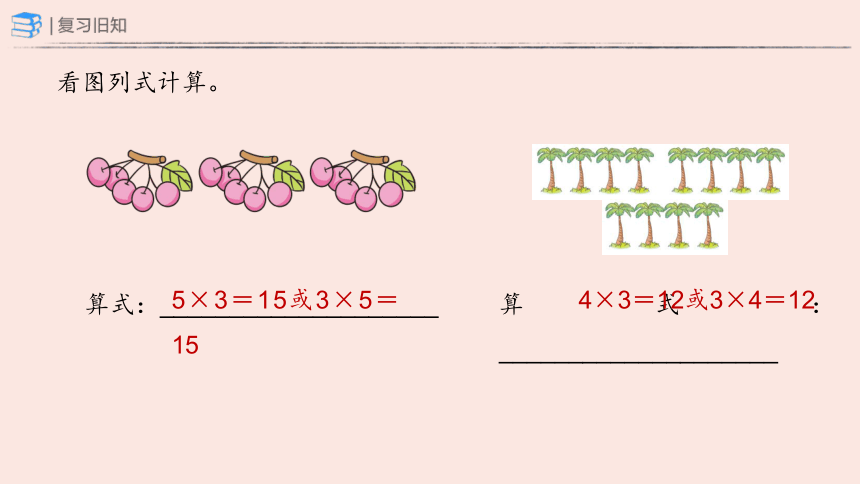

文档简介
(共24张PPT)
人教版二年级数学上册
4.2.3 乘加、乘减
算式:____________________
5×3=15或3×5=15
算式:____________________
看图列式计算。
4×3=12或3×4=12
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
3
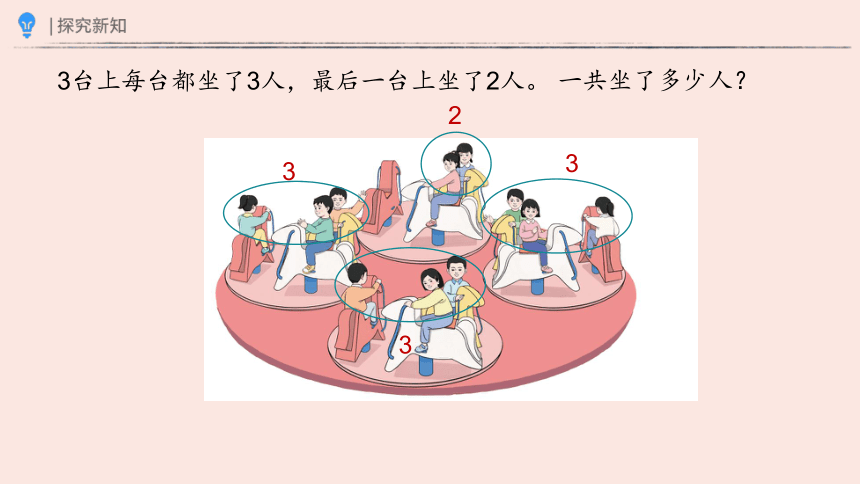
3台上每台都坐了3人,最后一台上坐了2人。
3
3
2
一共坐了多少人?
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
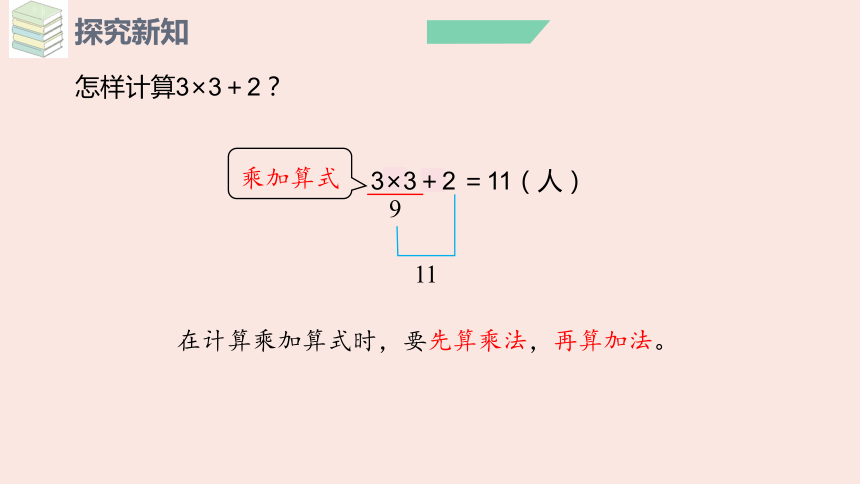
怎样计算3×3+2?
3×3+2
9
11
=11(人)
乘加算式
在计算乘加算式时,要先算乘法,再算加法。
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
学习任务一
(1)利用手中的学具摆一摆或画一画等方式表示出对情境的理解。
(2)独立列出算式。
(3)和同桌相互说一说自己的想法。
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
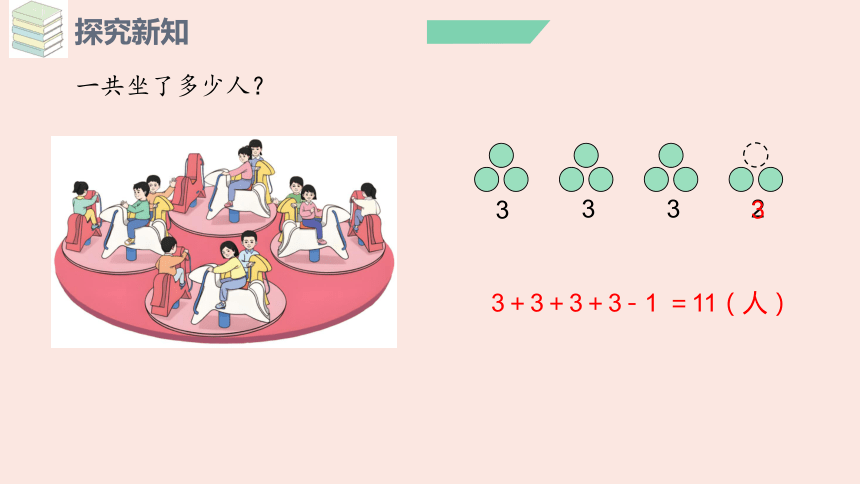
一共坐了多少人?
3
3
3
2
3
3+3+3+3
-1
=11(人)
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
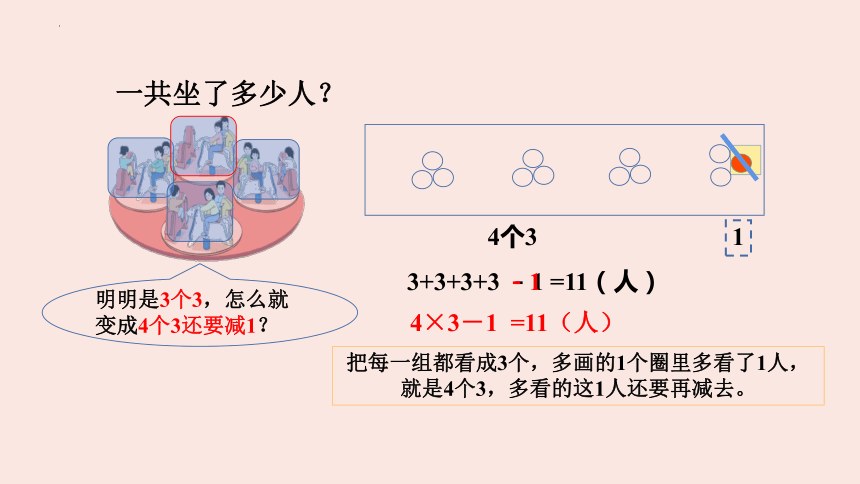
4×3-1 =11(人)
4个3
1
3+3+3+3 -1 =11(人)
明明是3个3,怎么就变成4个3还要减1?
把每一组都看成3个,多画的1个圈里多看了1人,就是4个3,多看的这1人还要再减去。
-1
一共坐了多少人?
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
一共坐了多少人?
3
3
3
3
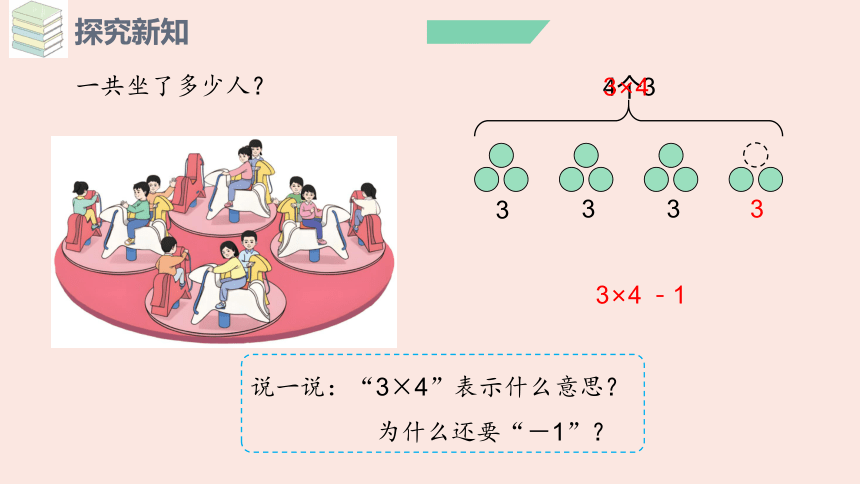
3×4
-1
4个3
3×4
说一说:“3×4”表示什么意思?
为什么还要“-1”?
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
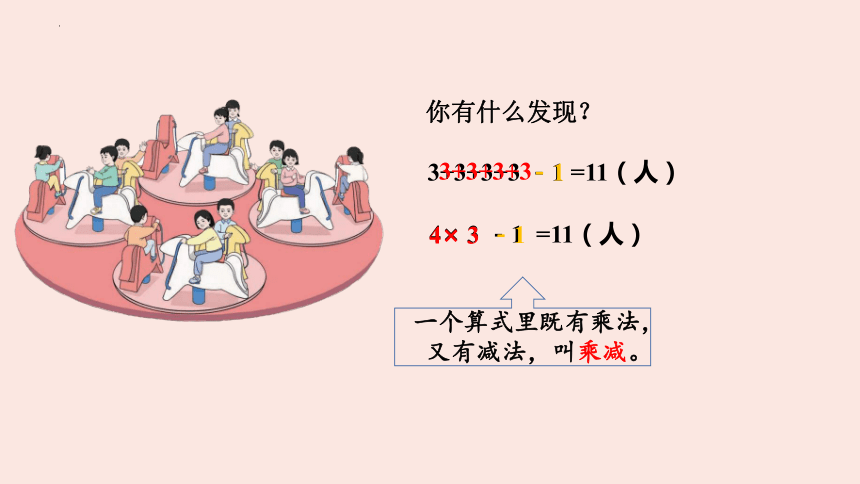
4× 3 -1 =11(人)
3+3+3+3 -1 =11(人)
你有什么发现?
3+3+3+3
4× 3
-1
-1
一个算式里既有乘法,
又有减法,叫乘减。
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
怎样计算3×4-1?
3×4-1
12
11
=11(人)
乘减算式
在计算乘减算式时,要先算乘法,再算减法。
4× 3 -1 =11(人)
3× 3+2=11(人)
9
12
既有乘又有加(减),先算什么,再算什么?
既有乘又有加(减),先算乘法,再算加(减)法。
小结:在乘加、乘减算式中,要先算乘法,再算加法或减法。
课堂小结
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
你更喜欢哪一种?
3+3+3+2=11
3×3+2=11
3+3+3+3-1=11
3×4-1=11
同一个问题,思考的角度不同,列出的算式一般也不同。但计算的结果都是相同的。
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
4× 3 -1 =11(人)
3× 3+2=11(人)
9
12
既有乘又有加(减),先算什么,再算什么?
既有乘又有加(减),先算乘法,再算加(减)法。
小结:在乘加、乘减算式中,要先算乘法,再算加法或减法。
课堂小结
5×5
-2
=23
4×6
-2
=22
小丽
教材第59页“练习十二”第5题
谁涂色的个数多?说说你是怎样比较的。
☆
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
训练与应用
一共停了多少辆车?
多种方法解决问题
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
3×4-1
12
11
=11
3×3+2
9
11
=11
在计算乘加、乘减算式时,都是先算的什么?
在计算乘加、乘减算式时,要先算乘法,再算加法或减法。
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
一共停了多少辆车?
4个3
1
1
3个4
3
4个2
3个3
2
4× 3-2=11(人)
3× 3+2=11(人)
3× 4-1=11(人)
4× 2+3=11(人)
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
1
一共有多少人?
方法一:
5×4+4=24(人)
方法二:
5×5-1=24(人)
答:一共有24人。
教材第59页“练习十二”第4题
2.看图填写合适的数和运算符号。
×
=
3
-
5
2
13
3
+
4
1
13
×
=
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
3
你能用乘法口诀直接计算得数吗?
6×4-4可以看作6个4减去1个4,还剩5个4,也就是5×4或4×5。
6×4-4=
× =
5
4
20
3×3+2×3=
× =
口诀:
四五二十
口诀:
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
4
找规律,填一填。
33
3
一共坐了多少人?
3+3+3+2=11(人)
3×3+2=11(人)
3×4-1=11(人)
这几种方法,你们觉得哪种更简便?
课堂小结
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
1.乘加、乘减算式
(1)像3×3+2这样的有乘、有加的算式,是乘加算式。
(2)像3×4-1这样的有乘、有减的算式,是乘减算式。
2.计算乘加或乘减算式
要先算乘法,后算加法或减法。
乘加、乘减
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
人教版二年级数学上册
4.2.3 乘加、乘减
算式:____________________
5×3=15或3×5=15
算式:____________________
看图列式计算。
4×3=12或3×4=12
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
3
3台上每台都坐了3人,最后一台上坐了2人。
3
3
2
一共坐了多少人?
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
怎样计算3×3+2?
3×3+2
9
11
=11(人)
乘加算式
在计算乘加算式时,要先算乘法,再算加法。
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
学习任务一
(1)利用手中的学具摆一摆或画一画等方式表示出对情境的理解。
(2)独立列出算式。
(3)和同桌相互说一说自己的想法。
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
一共坐了多少人?
3
3
3
2
3
3+3+3+3
-1
=11(人)
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
4×3-1 =11(人)
4个3
1
3+3+3+3 -1 =11(人)
明明是3个3,怎么就变成4个3还要减1?
把每一组都看成3个,多画的1个圈里多看了1人,就是4个3,多看的这1人还要再减去。
-1
一共坐了多少人?
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
一共坐了多少人?
3
3
3
3
3×4
-1
4个3
3×4
说一说:“3×4”表示什么意思?
为什么还要“-1”?
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
4× 3 -1 =11(人)
3+3+3+3 -1 =11(人)
你有什么发现?
3+3+3+3
4× 3
-1
-1
一个算式里既有乘法,
又有减法,叫乘减。
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
怎样计算3×4-1?
3×4-1
12
11
=11(人)
乘减算式
在计算乘减算式时,要先算乘法,再算减法。
4× 3 -1 =11(人)
3× 3+2=11(人)
9
12
既有乘又有加(减),先算什么,再算什么?
既有乘又有加(减),先算乘法,再算加(减)法。
小结:在乘加、乘减算式中,要先算乘法,再算加法或减法。
课堂小结
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
你更喜欢哪一种?
3+3+3+2=11
3×3+2=11
3+3+3+3-1=11
3×4-1=11
同一个问题,思考的角度不同,列出的算式一般也不同。但计算的结果都是相同的。
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
4× 3 -1 =11(人)
3× 3+2=11(人)
9
12
既有乘又有加(减),先算什么,再算什么?
既有乘又有加(减),先算乘法,再算加(减)法。
小结:在乘加、乘减算式中,要先算乘法,再算加法或减法。
课堂小结
5×5
-2
=23
4×6
-2
=22
小丽
教材第59页“练习十二”第5题
谁涂色的个数多?说说你是怎样比较的。
☆
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
训练与应用
一共停了多少辆车?
多种方法解决问题
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
3×4-1
12
11
=11
3×3+2
9
11
=11
在计算乘加、乘减算式时,都是先算的什么?
在计算乘加、乘减算式时,要先算乘法,再算加法或减法。
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
一共停了多少辆车?
4个3
1
1
3个4
3
4个2
3个3
2
4× 3-2=11(人)
3× 3+2=11(人)
3× 4-1=11(人)
4× 2+3=11(人)
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
1
一共有多少人?
方法一:
5×4+4=24(人)
方法二:
5×5-1=24(人)
答:一共有24人。
教材第59页“练习十二”第4题
2.看图填写合适的数和运算符号。
×
=
3
-
5
2
13
3
+
4
1
13
×
=
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
3
你能用乘法口诀直接计算得数吗?
6×4-4可以看作6个4减去1个4,还剩5个4,也就是5×4或4×5。
6×4-4=
× =
5
4
20
3×3+2×3=
× =
口诀:
四五二十
口诀:
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
4
找规律,填一填。
33
3
一共坐了多少人?
3+3+3+2=11(人)
3×3+2=11(人)
3×4-1=11(人)
这几种方法,你们觉得哪种更简便?
课堂小结
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
1.乘加、乘减算式
(1)像3×3+2这样的有乘、有加的算式,是乘加算式。
(2)像3×4-1这样的有乘、有减的算式,是乘减算式。
2.计算乘加或乘减算式
要先算乘法,后算加法或减法。
乘加、乘减
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
古之成大事者,不惟有超世之才,亦有坚忍不拔之志
