苏教版小学数学五年级下册8.3《整理与复习——图形王国》课件(共37张PPT)
文档属性
| 名称 | 苏教版小学数学五年级下册8.3《整理与复习——图形王国》课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 20:48:48 | ||
图片预览






文档简介
(共37张PPT)
整理与复习
图形王国
八
苏教版数学五年级(下)
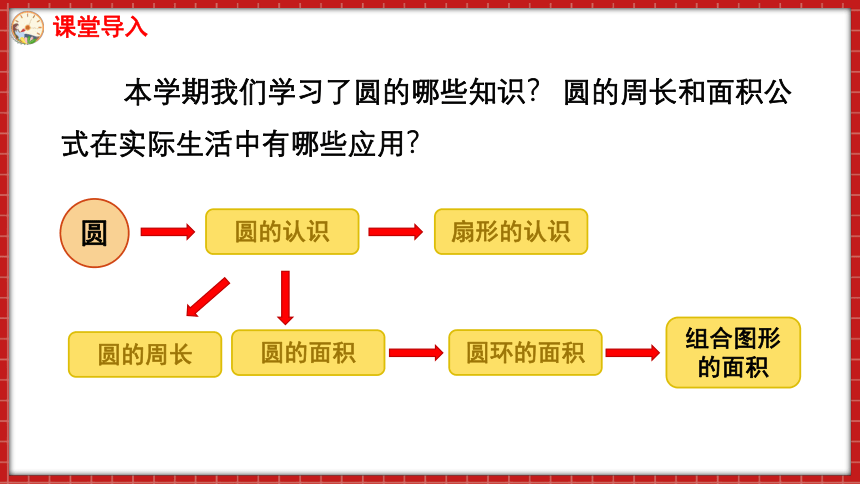
本学期我们学习了圆的哪些知识? 圆的周长和面积公式在实际生活中有哪些应用?
圆
圆的认识
扇形的认识
圆的周长
圆的面积
圆环的面积
组合图形的面积
课堂导入
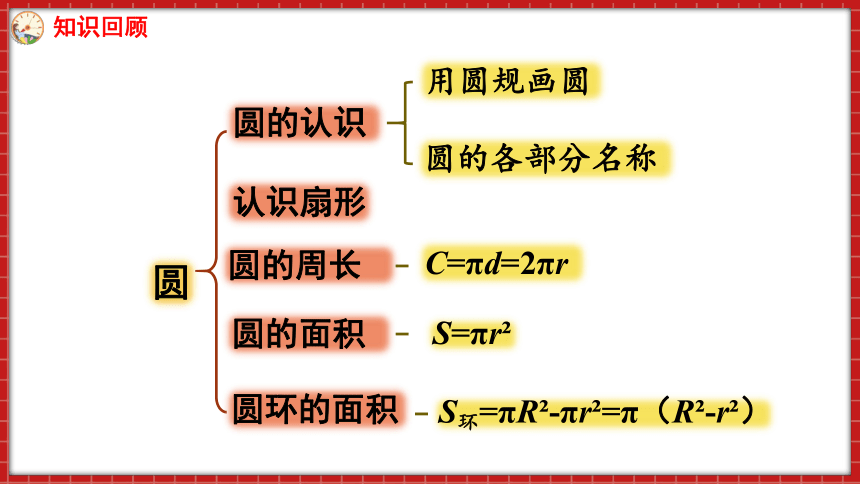
圆
圆的认识
认识扇形
圆的周长
圆环的面积
圆的面积
用圆规画圆
圆的各部分名称
C=πd=2πr
S=πr
S环=πR -πr =π(R -r )
知识回顾
圆是由一条曲线围成的封闭的平面图形。
圆的认识
知识回顾
第一步:把圆规的两脚分开,
定好两脚间的距离(即半径);
第二步:把有针尖的一脚固
定在圆心上;
第三步:把装有铅笔的一脚旋转一周,
就画出一个圆。
① 定长
② 定点
③ 旋转一周
用圆规画圆
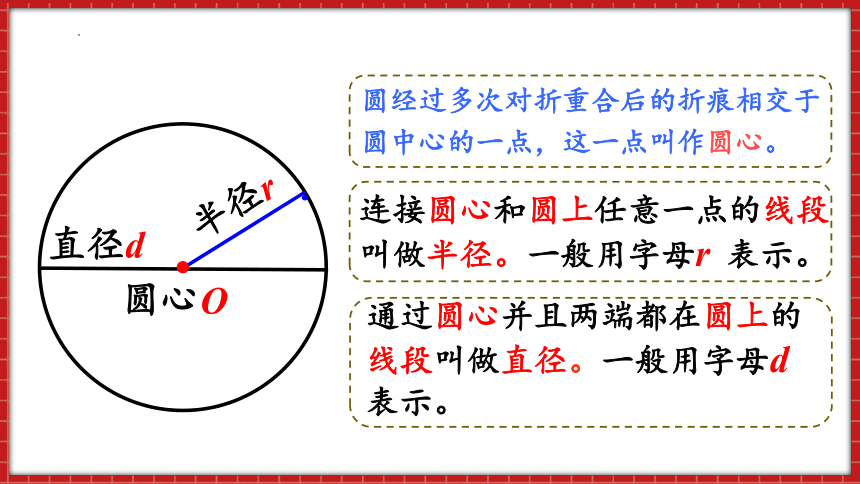
连接圆心和圆上任意一点的线段叫做半径。一般用字母r 表示。
通过圆心并且两端都在圆上的线段叫做直径。一般用字母d 表示。
O
圆心
半径r
直径d
圆经过多次对折重合后的折痕相交于圆中心的一点,这一点叫作圆心。
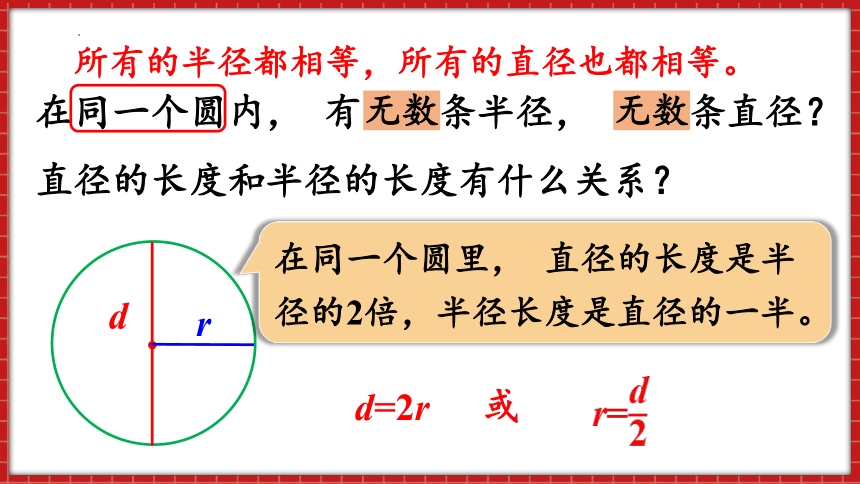
在同一个圆内, 有多少条半径, 多少条直径?
直径的长度和半径的长度有什么关系?
r
无数
d
无数
所有的半径都相等,所有的直径也都相等。
在同一个圆里, 直径的长度是半径的2倍,半径长度是直径的一半。
d=2r
r=
或
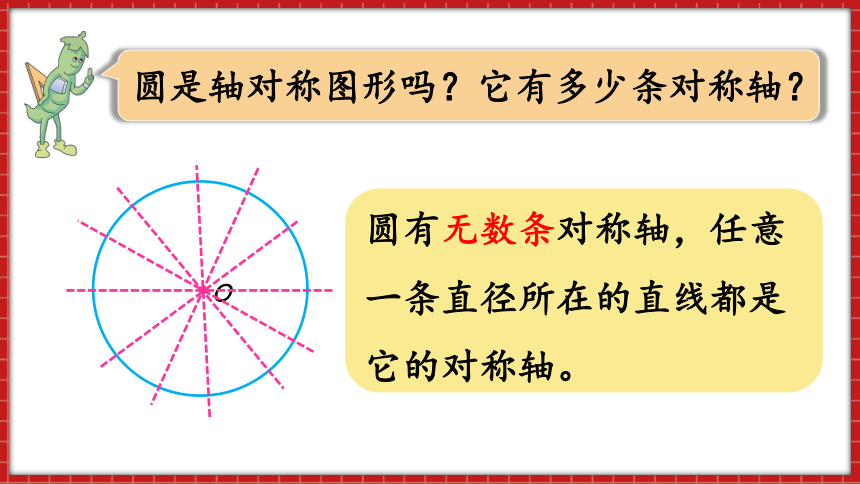
圆是轴对称图形吗?它有多少条对称轴?
两边可以重合,圆是轴对称图形。
把圆沿任意一条直径对折。
圆是轴对称图形吗?它有多少条对称轴?
O
圆有无数条对称轴,任意一条直径所在的直线都是它的对称轴。
如下图,在一个长为8厘米的长方形内,有2个大小相等的圆。
(1)求圆的半径;
(2)求长方形的面积。
(1)8÷2÷2=2(厘米)
答:圆的半径为2厘米。
(2)8÷2×8=32(平方厘米)
答:长方形的面积为32平方厘米。
典例讲解
A
B
O
圆心角
半径
半径
弧
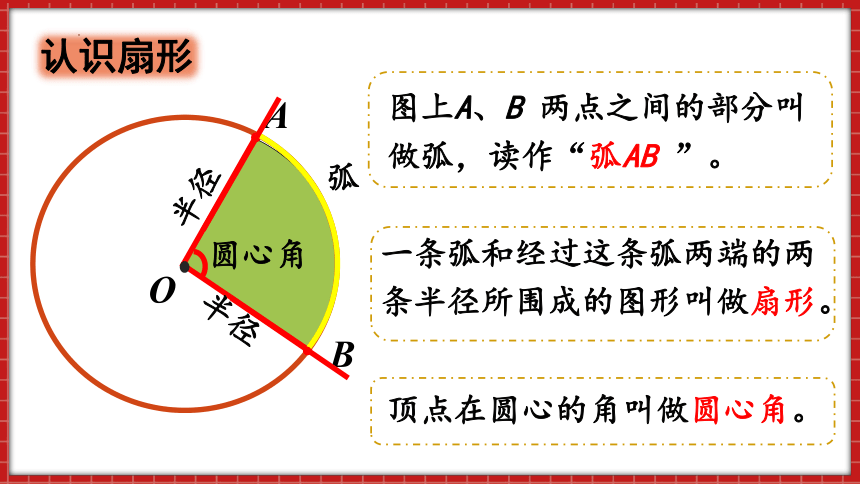
图上A、B 两点之间的部分叫做弧,读作“弧AB ”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
认识扇形
在同一个圆中,扇形的大小与什么有关系呢?
O
在同一个圆里,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
圆心角相等时,半径越大扇形就越大。
圆心角
同一个圆里
圆心角越大,扇形就越大
先画一个圆,再在圆上画一个扇形,并剪下来,折一折,说说你发现了什么?
扇形是轴对称图形,经过圆心和弧的中心的直线是对称轴。
只有1条对称轴
在扇形下面的括号里画“√”。
√
典例讲解
围成圆的曲线的长是圆的周长。
圆的周长指什么?
圆的周长
如果用C 表示圆的周长,d 表示直径,r 表示半径,就有:
C =πd
=圆周率
圆的周长=圆周率×直径
圆的周长=圆周率×半径×2
圆的周长
直径
C=2πr
或
1.3.14是r的近似值,不能说π=3.14;
2.周长是直径的倍,而不是3.14倍;
3.圆周率(π)是一个固定的数,与圆的大小无关。
希望小学有一个直径为20米的大型花坛,要在周围围上栏杆,需要栏杆多少米?
C = πd =3.14×20=62.8(米)
答:需要栏杆62.8米。
典例讲解
C
2
r
C=2πr
把圆沿直径切成偶数等份,在拼成近似的长方形:
πr
圆的面积
r
因为: 长方形面积= 长 × 宽
所以: 圆的面积 = ×
πr
r
πr
=
如果用S表示圆的面积,那么圆的面积计算公式就是 :
S=πr
πr
幸福小学新修建一个直径为20米的圆形花坛,花坛的占地面积是多少平方米?
S = πr2 =3.14×102=314(平方米)
答:花坛的占地面积是314平方米。
20÷2=10(米)
典例讲解
圆环的面积
什么叫圆环?
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环。
r
R
环宽
外圆:圆环中较大的圆。外圆的半径一般用字母R表示。
O
内圆:圆环中较小的圆。内圆的半径一般用字母r表示。
环宽:两个圆之间的宽度。
环宽=外圆半径-内圆半径,即R-r。
(1)两个圆是同心圆,即圆心在同一点上。
圆环具有哪些特点?
(2)圆环是轴对称图形,有无数条对称轴。
(3)两个圆间的距离处处相等。
=
或 S环=π×(R2-r2)
S环
πR2
πr2
-
圆环的面积=外圆的面积-内圆的面积
减去
得到
要绕着一个直径为12米的圆形花坛铺一条宽1米的水泥路,这条路的面积是多少?
S = π(R2-r2 )
=3.14×(72-62)
=40.82(平方米)
答:这条路的面积是40.82平方米。
12÷2=6(米) 6+1=7(米)
典例讲解
1. 填一填。
(1)俞月在画圆时忘记测量圆规两脚尖之间的距离,于是她用如图的方法去测量。画这个圆时,圆规两脚尖之间的距离是( 1 )厘米,圆的周长是
( 6.28 )厘米,面积是( 3.14 )平方厘米。
1
6.28
3.14
课堂练习
(2)一个圆的周长是31.4厘米,它的半径是( 5 )厘米,它的面积是( 78.5 )平方厘米。
(3)在一个直径为6米的圆形花坛的四周有一条宽2米的水泥路,这条水泥路面的面积是( 50.24 )平方米。在水泥路的内侧加一圈木制的护栏,至少需要
( 18.84 )米长的护栏。
5
78.5
50.24
18.84
(4)一个圆的直径扩大到原来的4倍,它的周长扩大到原来的( 4 )倍,面积扩大到原来的
( 16 )倍。
(5)用一根14米长的绳子绕一棵大树围了10圈还余1.44米,这棵大树树干的横截面直径大约是
( 0.4 )米。
4
16
0.4
2.求如图中各涂色部分的周长。
(1) (2)
(1)3.14×3×2÷2+3.14×2×2÷2=15.7(cm)
2+3+(3-2)=6(cm)
15.7+6=21.7(cm)
(2)3.14×8÷2+15×2+8=50.56(厘米)
(3)
4×(4×2)-3.14×(4÷2)2×2=6.88(平方米)
3.14×42÷2-3.14×(4÷2)2÷2-4×4÷2=10.84(平方米)
3. 从一个长是8厘米、宽是5厘米的长方形中,剪下一个最大的半圆,半圆的面积是多少平方厘米
8÷2=4(厘米)
3.14×42÷2=25.12(平方厘米)
4. 如图,利用两面墙作边,用栅栏围成一个扇形羊圈。已知羊圈的直径是10米,求围成羊圈需要多少米的栅栏。
3.14×10÷4×3=23.55(米)
5.蓝湾公园里有一个周长为62.8 m的圆形草坪,管理处准
备安装一个自动旋转喷水龙头进行喷灌。现有射程为20 m、
15 m、10 m的三种装置,你认为选哪种射程的装置比较合适?这种射程的装置能喷灌的面积有多大?
62.8÷3.14÷2=10(m)
3.14×102=314(m2)
答:选射程为10 m的装置比较合适,能喷灌的面积是
314 m2。
6.甲、乙两人从圆形街心花园的同一地点同时出发,反向而
行,10分钟后两人首次相遇,甲每分钟走76米,乙每分钟走81
米。这个圆形街心花园的占地面积是多少?
花园的周长:(76+81)×10=1570(米)
花园的半径:1570÷3.14÷2=250(米)
面积:3.14×2502=196250(平方米)
答:这个圆形街心花园的占地面积是196250平方米。
1.有8个半径为1厘米的小圆,用它们的圆周的一部分连成
一个花瓣图形(如图),点A、点B、点C、点D、点E、点F、
点G、点O为这些圆的圆心,花瓣图形的周长和面积分别是多少?
周长:2×3.14×1×2+2×3.14×1÷4×3×4=31.4(厘米)
面积:(1×4)×(1×4)+3.14×12=19.14(平方厘米)
答:花瓣图形的周长是31.4厘米,面积是19.14平方厘米。
思维拓展
2. 如图,大圆的半径是6厘米,小圆的半径是2厘米。现让小圆沿着大圆滚动一周。
(1)小圆的圆心走过的路程是多少厘米
(2)小圆滚过的面的面积是多少平方厘米
(1)小圆的圆心走过的路程是多少厘米
3.14×(6+2)×2=50.24(厘米)
(2)小圆滚过的面的面积是多少平方厘米
6+2×2=10(厘米)
3.14×(102-62)=200.96(平方厘米)
整理与复习
图形王国
八
苏教版数学五年级(下)
本学期我们学习了圆的哪些知识? 圆的周长和面积公式在实际生活中有哪些应用?
圆
圆的认识
扇形的认识
圆的周长
圆的面积
圆环的面积
组合图形的面积
课堂导入
圆
圆的认识
认识扇形
圆的周长
圆环的面积
圆的面积
用圆规画圆
圆的各部分名称
C=πd=2πr
S=πr
S环=πR -πr =π(R -r )
知识回顾
圆是由一条曲线围成的封闭的平面图形。
圆的认识
知识回顾
第一步:把圆规的两脚分开,
定好两脚间的距离(即半径);
第二步:把有针尖的一脚固
定在圆心上;
第三步:把装有铅笔的一脚旋转一周,
就画出一个圆。
① 定长
② 定点
③ 旋转一周
用圆规画圆
连接圆心和圆上任意一点的线段叫做半径。一般用字母r 表示。
通过圆心并且两端都在圆上的线段叫做直径。一般用字母d 表示。
O
圆心
半径r
直径d
圆经过多次对折重合后的折痕相交于圆中心的一点,这一点叫作圆心。
在同一个圆内, 有多少条半径, 多少条直径?
直径的长度和半径的长度有什么关系?
r
无数
d
无数
所有的半径都相等,所有的直径也都相等。
在同一个圆里, 直径的长度是半径的2倍,半径长度是直径的一半。
d=2r
r=
或
圆是轴对称图形吗?它有多少条对称轴?
两边可以重合,圆是轴对称图形。
把圆沿任意一条直径对折。
圆是轴对称图形吗?它有多少条对称轴?
O
圆有无数条对称轴,任意一条直径所在的直线都是它的对称轴。
如下图,在一个长为8厘米的长方形内,有2个大小相等的圆。
(1)求圆的半径;
(2)求长方形的面积。
(1)8÷2÷2=2(厘米)
答:圆的半径为2厘米。
(2)8÷2×8=32(平方厘米)
答:长方形的面积为32平方厘米。
典例讲解
A
B
O
圆心角
半径
半径
弧
图上A、B 两点之间的部分叫做弧,读作“弧AB ”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
认识扇形
在同一个圆中,扇形的大小与什么有关系呢?
O
在同一个圆里,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
圆心角相等时,半径越大扇形就越大。
圆心角
同一个圆里
圆心角越大,扇形就越大
先画一个圆,再在圆上画一个扇形,并剪下来,折一折,说说你发现了什么?
扇形是轴对称图形,经过圆心和弧的中心的直线是对称轴。
只有1条对称轴
在扇形下面的括号里画“√”。
√
典例讲解
围成圆的曲线的长是圆的周长。
圆的周长指什么?
圆的周长
如果用C 表示圆的周长,d 表示直径,r 表示半径,就有:
C =πd
=圆周率
圆的周长=圆周率×直径
圆的周长=圆周率×半径×2
圆的周长
直径
C=2πr
或
1.3.14是r的近似值,不能说π=3.14;
2.周长是直径的倍,而不是3.14倍;
3.圆周率(π)是一个固定的数,与圆的大小无关。
希望小学有一个直径为20米的大型花坛,要在周围围上栏杆,需要栏杆多少米?
C = πd =3.14×20=62.8(米)
答:需要栏杆62.8米。
典例讲解
C
2
r
C=2πr
把圆沿直径切成偶数等份,在拼成近似的长方形:
πr
圆的面积
r
因为: 长方形面积= 长 × 宽
所以: 圆的面积 = ×
πr
r
πr
=
如果用S表示圆的面积,那么圆的面积计算公式就是 :
S=πr
πr
幸福小学新修建一个直径为20米的圆形花坛,花坛的占地面积是多少平方米?
S = πr2 =3.14×102=314(平方米)
答:花坛的占地面积是314平方米。
20÷2=10(米)
典例讲解
圆环的面积
什么叫圆环?
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环。
r
R
环宽
外圆:圆环中较大的圆。外圆的半径一般用字母R表示。
O
内圆:圆环中较小的圆。内圆的半径一般用字母r表示。
环宽:两个圆之间的宽度。
环宽=外圆半径-内圆半径,即R-r。
(1)两个圆是同心圆,即圆心在同一点上。
圆环具有哪些特点?
(2)圆环是轴对称图形,有无数条对称轴。
(3)两个圆间的距离处处相等。
=
或 S环=π×(R2-r2)
S环
πR2
πr2
-
圆环的面积=外圆的面积-内圆的面积
减去
得到
要绕着一个直径为12米的圆形花坛铺一条宽1米的水泥路,这条路的面积是多少?
S = π(R2-r2 )
=3.14×(72-62)
=40.82(平方米)
答:这条路的面积是40.82平方米。
12÷2=6(米) 6+1=7(米)
典例讲解
1. 填一填。
(1)俞月在画圆时忘记测量圆规两脚尖之间的距离,于是她用如图的方法去测量。画这个圆时,圆规两脚尖之间的距离是( 1 )厘米,圆的周长是
( 6.28 )厘米,面积是( 3.14 )平方厘米。
1
6.28
3.14
课堂练习
(2)一个圆的周长是31.4厘米,它的半径是( 5 )厘米,它的面积是( 78.5 )平方厘米。
(3)在一个直径为6米的圆形花坛的四周有一条宽2米的水泥路,这条水泥路面的面积是( 50.24 )平方米。在水泥路的内侧加一圈木制的护栏,至少需要
( 18.84 )米长的护栏。
5
78.5
50.24
18.84
(4)一个圆的直径扩大到原来的4倍,它的周长扩大到原来的( 4 )倍,面积扩大到原来的
( 16 )倍。
(5)用一根14米长的绳子绕一棵大树围了10圈还余1.44米,这棵大树树干的横截面直径大约是
( 0.4 )米。
4
16
0.4
2.求如图中各涂色部分的周长。
(1) (2)
(1)3.14×3×2÷2+3.14×2×2÷2=15.7(cm)
2+3+(3-2)=6(cm)
15.7+6=21.7(cm)
(2)3.14×8÷2+15×2+8=50.56(厘米)
(3)
4×(4×2)-3.14×(4÷2)2×2=6.88(平方米)
3.14×42÷2-3.14×(4÷2)2÷2-4×4÷2=10.84(平方米)
3. 从一个长是8厘米、宽是5厘米的长方形中,剪下一个最大的半圆,半圆的面积是多少平方厘米
8÷2=4(厘米)
3.14×42÷2=25.12(平方厘米)
4. 如图,利用两面墙作边,用栅栏围成一个扇形羊圈。已知羊圈的直径是10米,求围成羊圈需要多少米的栅栏。
3.14×10÷4×3=23.55(米)
5.蓝湾公园里有一个周长为62.8 m的圆形草坪,管理处准
备安装一个自动旋转喷水龙头进行喷灌。现有射程为20 m、
15 m、10 m的三种装置,你认为选哪种射程的装置比较合适?这种射程的装置能喷灌的面积有多大?
62.8÷3.14÷2=10(m)
3.14×102=314(m2)
答:选射程为10 m的装置比较合适,能喷灌的面积是
314 m2。
6.甲、乙两人从圆形街心花园的同一地点同时出发,反向而
行,10分钟后两人首次相遇,甲每分钟走76米,乙每分钟走81
米。这个圆形街心花园的占地面积是多少?
花园的周长:(76+81)×10=1570(米)
花园的半径:1570÷3.14÷2=250(米)
面积:3.14×2502=196250(平方米)
答:这个圆形街心花园的占地面积是196250平方米。
1.有8个半径为1厘米的小圆,用它们的圆周的一部分连成
一个花瓣图形(如图),点A、点B、点C、点D、点E、点F、
点G、点O为这些圆的圆心,花瓣图形的周长和面积分别是多少?
周长:2×3.14×1×2+2×3.14×1÷4×3×4=31.4(厘米)
面积:(1×4)×(1×4)+3.14×12=19.14(平方厘米)
答:花瓣图形的周长是31.4厘米,面积是19.14平方厘米。
思维拓展
2. 如图,大圆的半径是6厘米,小圆的半径是2厘米。现让小圆沿着大圆滚动一周。
(1)小圆的圆心走过的路程是多少厘米
(2)小圆滚过的面的面积是多少平方厘米
(1)小圆的圆心走过的路程是多少厘米
3.14×(6+2)×2=50.24(厘米)
(2)小圆滚过的面的面积是多少平方厘米
6+2×2=10(厘米)
3.14×(102-62)=200.96(平方厘米)
