立体几何中的向量方法(3)
图片预览





文档简介
课件25张PPT。3.2 立体几何中的向量方法(3)xxz----利用向量解决平行与垂直问题一、复习1、用空间向量解决立体几何问题的“三步曲” (1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题; (2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(3)把向量的运算结果“翻译”成相应的几何意义。(化为向量问题)(进行向量运算)(回到图形问题)2、平行与垂直关系的向量表示(1)平行关系线线平行线面平行面面平行点击点击点击 (2)垂直关系线线垂直线面垂直面面垂直点击点击点击二、新课
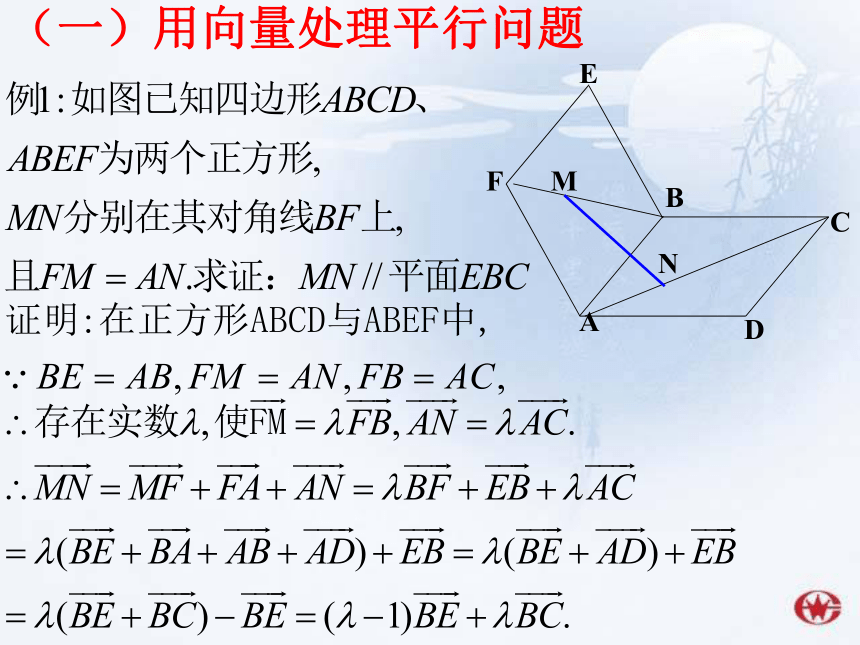
(一)用向量处理平行问题(二)用向量处理垂直问题(一)用向量处理平行问题评注:
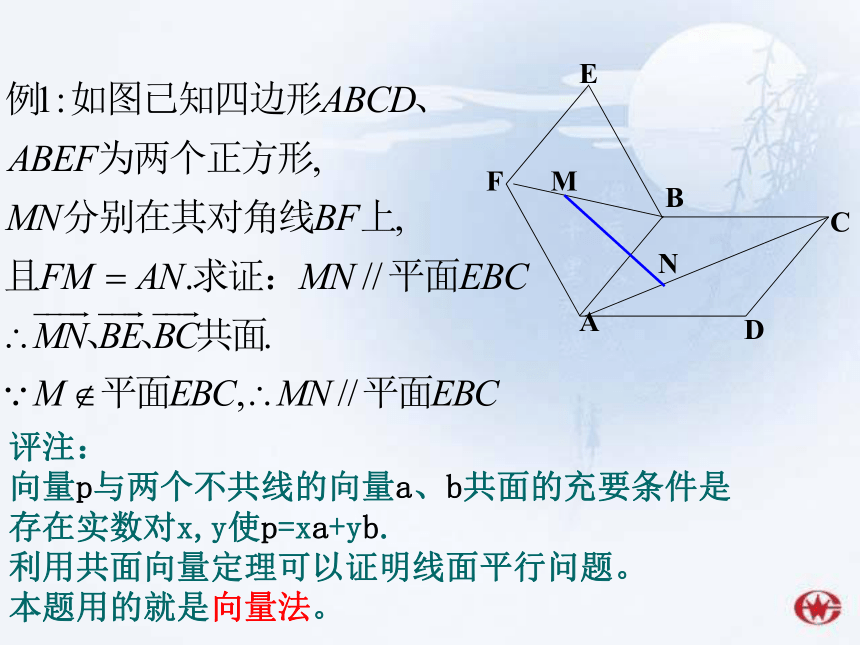
向量p与两个不共线的向量a、b共面的充要条件是
存在实数对x,y使p=xa+yb.
利用共面向量定理可以证明线面平行问题。
本题用的就是向量法。
XYZXYZ评注:
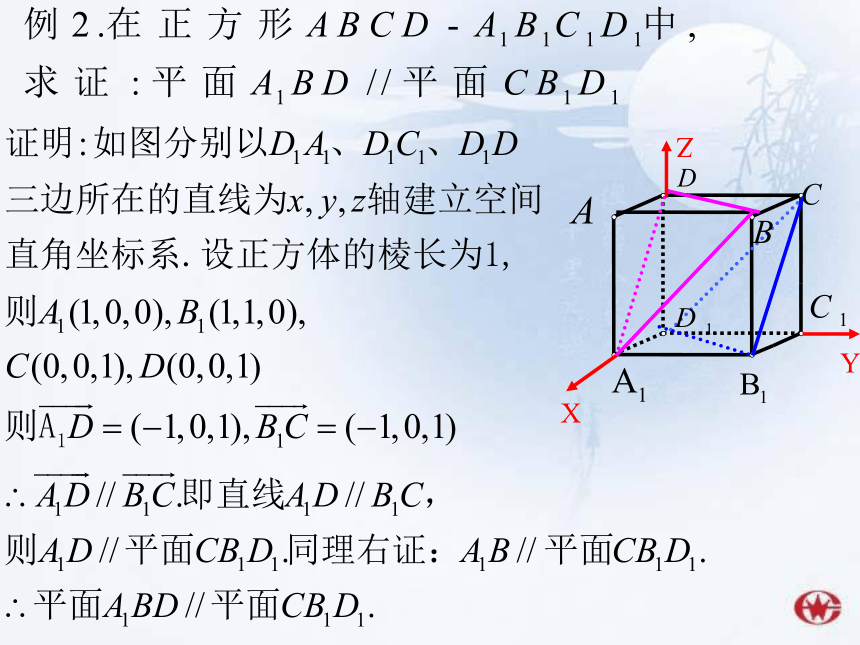
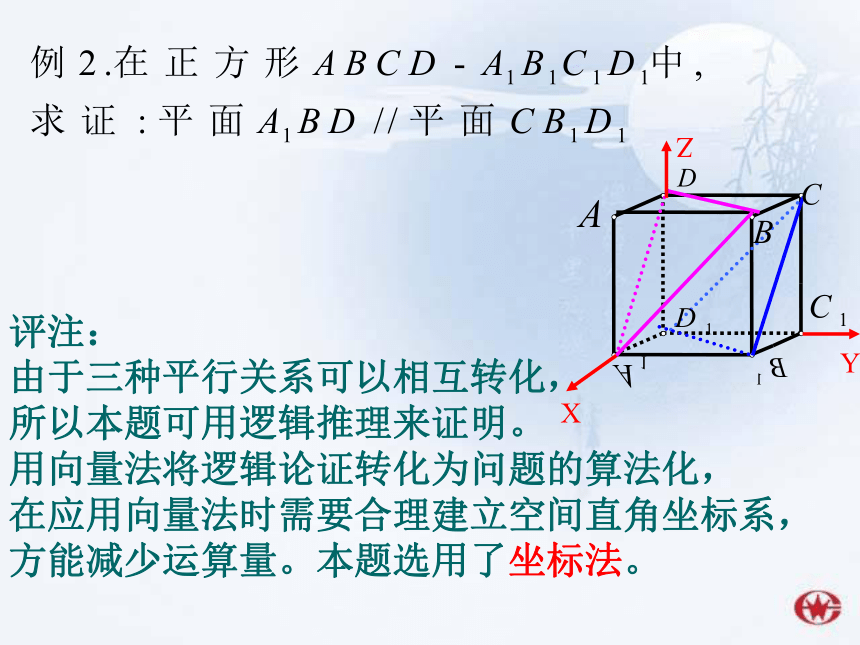
由于三种平行关系可以相互转化,
所以本题可用逻辑推理来证明。
用向量法将逻辑论证转化为问题的算法化,
在应用向量法时需要合理建立空间直角坐标系,
方能减少运算量。本题选用了坐标法。
(二)用向量处理垂直问题FEXYZFEXYZFEXYZ评注:
本题若用一般法证明,
容易证A’F垂直于BD,
而证A’F垂直于DE,
或证A’F垂直于EF则较难,
用建立空间坐标系的方法
能使问题化难为易。
向量法坐标法三、小结利用向量解决平行与垂直问题
向量法:利用向量的概念技巧运算解决问 题。
坐标法:利用数及其运算解决问题。
两种方法经常结合起来使用。XYZ四、作业 1.XYZ1.作业:2.课本p.116第2题。Bye-bye!lmllml
向量p与两个不共线的向量a、b共面的充要条件是
存在实数对x,y使p=xa+yb.
利用共面向量定理可以证明线面平行问题。
本题用的就是向量法。
XYZXYZ评注:
由于三种平行关系可以相互转化,
所以本题可用逻辑推理来证明。
用向量法将逻辑论证转化为问题的算法化,
在应用向量法时需要合理建立空间直角坐标系,
方能减少运算量。本题选用了坐标法。
(二)用向量处理垂直问题FEXYZFEXYZFEXYZ评注:
本题若用一般法证明,
容易证A’F垂直于BD,
而证A’F垂直于DE,
或证A’F垂直于EF则较难,
用建立空间坐标系的方法
能使问题化难为易。
向量法坐标法三、小结利用向量解决平行与垂直问题
向量法:利用向量的概念技巧运算解决问 题。
坐标法:利用数及其运算解决问题。
两种方法经常结合起来使用。XYZ四、作业 1.XYZ1.作业:2.课本p.116第2题。Bye-bye!lmllml
