期末应用题易错专项:分数四则混合运算-数学六年级上册苏教版(含答案)
文档属性
| 名称 | 期末应用题易错专项:分数四则混合运算-数学六年级上册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 537.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 09:39:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末应用题易错专项:分数四则混合运算-数学六年级上册苏教版
1.甲、乙两城相距480千米,一辆汽车上午9:00从甲城开往乙城,4小时行了全程的,照这样计算,这辆汽车在下午三点之前能否到达乙城?
2.家里的菜地共450平方米,王大爷准备用种番茄,按4∶9的面积比种黄瓜与番茄,黄瓜的种植面积是多少平方米?
3.三信小学美术组有63人,比舞蹈组的人数多,舞蹈组有多少人?(列方程解)
4.两筐苹果共重126千克。从第一筐取出放入第二筐,两筐苹果就同样重。原来两筐苹果各重多少千克?
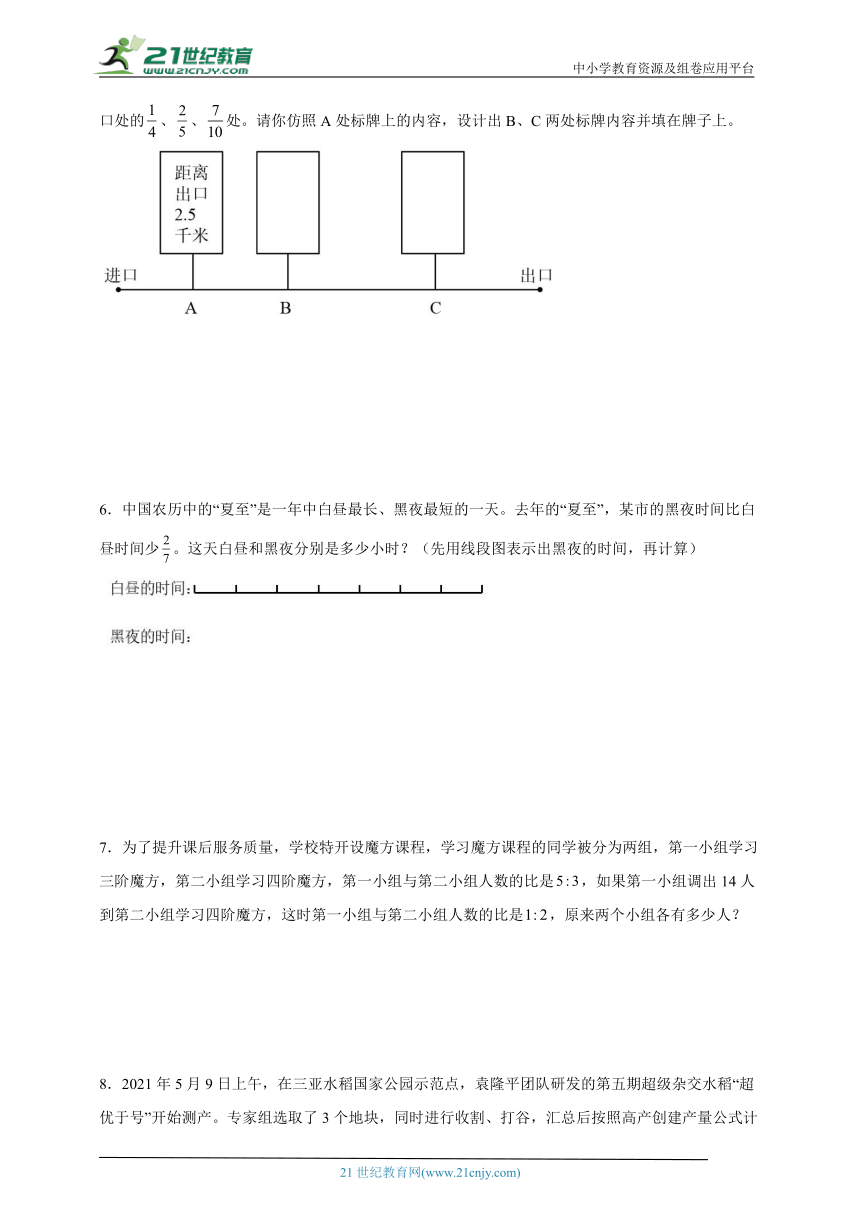
5.勺湖公园想在下图的A、B、C三个景点处各立一块标牌。A、B、C三个景点分别在从进口到出口处的、、处。请你仿照A处标牌上的内容,设计出B、C两处标牌内容并填在牌子上。
6.中国农历中的“夏至”是一年中白昼最长、黑夜最短的一天。去年的“夏至”,某市的黑夜时间比白昼时间少。这天白昼和黑夜分别是多少小时?(先用线段图表示出黑夜的时间,再计算)
7.为了提升课后服务质量,学校特开设魔方课程,学习魔方课程的同学被分为两组,第一小组学习三阶魔方,第二小组学习四阶魔方,第一小组与第二小组人数的比是,如果第一小组调出14人到第二小组学习四阶魔方,这时第一小组与第二小组人数的比是,原来两个小组各有多少人?
8.2021年5月9日上午,在三亚水稻国家公园示范点,袁隆平团队研发的第五期超级杂交水稻“超优于号”开始测产。专家组选取了3个地块,同时进行收割、打谷,汇总后按照高产创建产量公式计算,最终测产结果约为每公顷15吨,比第二期超级杂交水稻的产量增产。第二期超级杂交水稻产量大约是每公顷多少吨?(列方程解答)
9.两个仓库共有空调3000台,如果从甲仓库调出放到乙仓库,那么甲乙两仓库的空调台数的比是2∶3,原来甲仓库有空调多少台?
10.一桶油连桶共重16.5千克,倒出油的后,连桶共重11.5千克,油桶重多少千克?
11.第二十届省运会将于2022年8月28日至9月5日在泰州举行。省运会比赛分为青少年部、高校部和职工部三个部分。第十九届省运会在青少年部设置了28个比赛项目,第二十届省运会在青少年部设置的比赛项目预计比上届多。第二十届省运会预计在青少年部设置多少个比赛项目?(先把线段图补充完整,再解答)
12.某校五年级甲、乙、丙三个班分别都是54人,其中甲班男生人数与乙班女生人数同样多,丙班女生占全班人数的。这三个班一共有女生多少人?
13.刘老师买了一个篮球和一个排球一共用去216元,排球的单价是篮球的。一个排球和一个篮球的价格分别是多少元?
14.学校举办春季运动会,参加比赛的运动员一共有162人。已知男运动员的人数比女运动员多,请你算一算,男、女运动员各有多少人?
15.小明看一本课外书,第一天看了全书的,第二天看了全书的,两天一共看了69页,这本书共有多少页?
16.甲、乙两筐苹果,甲筐中已卖出,乙筐中已卖出,两筐剩下的苹果数量正好相等,已知甲筐中原有苹果45个,乙筐中原有苹果多少个?
17.仓库运一批面粉,第一次运走总数的,第二次运走总数的,两次一共运走了49吨。这批面粉一共多少吨?
18.一件冲锋衣的原价是360元,在国庆促销活动中降价,活动结束后又提价。现在这件冲锋衣的价格和原来相等吗?
19.一桶油,第一次用去千克,第二次用去千克,第三次用去前两次总质量的。第三次用去多少千克?
20.水果店有12筐苹果和6筐香蕉,一共需1650元,每筐香蕉的价钱是苹果的。每筐苹果多少元?每筐香蕉多少元?
21.学校举行运动会,缺席的学生人数占出席学生人数的,后来又有一个学生请假回家,这时缺席学生人数占出席学生人数的。求现在还有多少学生。
参考答案:
1.不能
【分析】用480×,求出汽车4小时行驶的路程。再根据速度=路程÷时间,代入数据,求出汽车的速度,再根据时间=路程÷速度,求出甲城到乙城的时间,进而解答。
【详解】480÷(480×÷4)
=480÷(320÷4)
=480÷80
=6(小时)
上午9:00=9时
9时+6小时=15时=下午3时。下午三点之前不能到达乙城。
答:这辆汽车在下午三点之前不能到达乙城。
【点睛】根据速度、时间、路程三者关系已经求一个数的几分之几是多少的计算方法进行解答。
2.60平方米
【分析】把这块菜地的面积看作单位“1” 王大爷准备用种番茄,用这块地的面积× ,求出种番茄的面积;按4∶9的面积种黄瓜与番茄,把种黄瓜和番茄的面积分成4+9份,番茄占其中的9,即番茄占种番茄和黄瓜的,黄瓜占种番茄和黄瓜面积的,用种番茄的面积÷,求出种番茄和黄瓜的面积,再进一步求出种黄瓜的面积。
【详解】450×÷×
=135÷×
=135××
=195×
=60(平方米)
答:黄瓜的种植面积是60平方米。
【点睛】利用求一个数的几分之几的计算方法,已知一个数的几分之几是多少,求这个数的计算方法以及按比例分配的计算方法进行解答。
3.56人
【分析】把舞蹈组的人数看作单位“1”,美术小组的人数比舞蹈组的人数多,美术小组的人数是舞蹈组的(1+),用舞蹈组的人数×(1+)=美术组的人数,设舞蹈组有x人,列方程:x×(1+)=63,解方程,即可解答。
【详解】解:设舞蹈组有x人。
x×(1+)=63
x=63
x=63÷
x=63×
x=56
答:舞蹈组有56人。
【点睛】本题考查方程的实际应用,根据求比一个数多或少几分之几的数是多少的计算方法,设出未知数,找出相关的量,列方程,解方程。
4.第一筐重81千克;第二筐重45千克
【分析】从第一筐取出放入第二筐,两筐苹果就同样重,则现在每筐苹果的重量是126÷2=63(千克)。把原来第一筐苹果的重量看作单位“1”,取出后,现在的重量是原来重量的(1-),根据“已知一个数的几分之几是多少,求这个数,用除法计算”,用63除以(1-)即可求出原来第一筐苹果的重量。再用126减去原来第一筐的重量求出原来第二筐苹果的重量。
【详解】126÷2=63(千克)
第一筐:63÷(1-)
=63÷
=63×
=81(千克)
第二筐:126-81=45(千克)
答:原来第一筐苹果重81千克,第二筐重45千克。
【点睛】本题考查分数四则混合运算的应用。已知一个数的几分之几是多少,求这个数,用除法计算,据此先求出第一筐苹果现在的重量,以及现在的重量是原来重量的几分之几是解题的关键。
5.见详解
【分析】把进口与出口之间的距离看作单位“1”,A、B、C三个景点处各立一块标牌。A、B、C三个景点分别在从进口到出口处的、、,由此可知A景点距离出口2.5千米占进口与出口距离的(1-),用2.5÷(1-),求出进口与出口的距离;再用进口与出口的距离×(1-);进口与出口的距离×(1-),分别求出B、C各距离进口的距离,据此解答。
【详解】2.5÷(1-)
=2.5÷
=2.5×
=(千米)
×(1-)
=×
=2(千米)
×(1-)
=×
=1(千米)
所以B景点距离出口2千米,C景点距离出口1千米。
【点睛】解答本题的关键是单位“1”的确定,重点是求出进口与出口之间的距离,进而求出B景点距离出口多少千米,C景点距离出口多少千米。
6.图见详解
白昼:14小时;黑夜:10小时
【分析】把白昼时间看作单位“1”,根据题中的已知条件,白昼平均分成7段,黑夜比白昼少2段,则用线段画5段表示出黑夜的时间;把白昼的时间看作单位“1”,则黑夜的时间是白昼时间的(1-),用白昼时间×(1-),就是黑夜的时间,设白昼时间为x小时,则黑夜时间为(1-)x小时;白昼+黑夜=24小时,列方程:x+(1-)x=24,解方程,求出白昼的时间,进而求出黑夜的时间。
【详解】
解:设白昼的时间为x小时,则黑夜时间为(1-)x小时。
x+(1-)x=24
x+x=24
x=24
x=24÷
x=24×
x=14
24-14=10(小时)
答:白昼时间是14小时,黑夜时间是10小时。
【点睛】本题考查方程的实际应用。可以白昼与黑夜的时间关系,设出未知数,找出相关的量,列方程,解方程,注意一天是24小时,即白昼+黑夜=小时。
7.第一小组:30人;第二小组:18人
【分析】根据题意,把两个小组的总人数看作单位“1”,第二小组的人数原来占总人数的,现在第二小组的人数占总人数的,增加了总人数的(-),对应的是14人,用14÷(-),求出两个小组的总人数,进而求出原来各自小组有的人数。
【详解】14÷(-)
=14÷(-)
=14÷(-)
=14÷
=14×
=48(人)
第二小组:48×
=48×
=18(人)
第一小组:48-18=30(人)
答:原来第一小组有30人,第二小组有18人。
【点睛】本题主要找出不变的量作为单位“1”,求出14人所对应的分率,进而进行解答。
8.12吨
【分析】设第二期超级杂交水稻产量大约是每公顷x吨,则(1+)x等于15吨,列方程:(1+)x=15,解方程,即可解答。
【详解】解:设第二期超级杂交水稻产量大约是每公顷x吨。
(1+)x=15
x=15
x=15÷
x=15×
x=12
答:第二期超级杂交水稻产量大约是每公顷12吨。
【点睛】本题考查方程的实际应用,关键是找准题目中的等量关系。
9.1600台
【分析】两个仓库共有空调3000台,后来甲仓库与乙仓库的存空调台数数比是2∶3,一共是2+3=5份,先用3000台除以5份,求出每份的台数,进而分别求出甲仓后来的台数,甲仓后来的台数相当于原来的台数的(1-),据分数除法的意义求出甲仓库原来的台数。
【详解】3000÷(2+3)×2÷(1-)
=3000÷5×2÷
=1200÷
=1600(台)
答:原来甲仓库有1600台空调。
【点睛】解答此题的关键是明确:从甲仓库取出到乙仓库,甲、乙两个仓库的空调台数的和不变,再根据两者后来的比,按照按比分配的方法,分别求出它们后来的台数,再逆推出原来的台数。
10.1.5千克
【分析】用16.5-11.5,求出倒出油的重量,把这桶油的重量看作单位“1”,倒出油的,对应的是倒出油的重量,用倒出油的重量除以,求出这桶油的重量,再用这桶油连桶的重量-这桶油的重量,即可求出油桶的重量。
【详解】16.5-(16.5-11.5)÷
=16.5-5÷
=16.5-5×3
=16.5-15
=1.5(千克)
答:油桶重1.5千克。
【点睛】利用已知一个数的几分之几是多少,求这个数的知识进行解答,关键是求出倒出油的对应的油的重量。
11.图见详解;36个
【分析】根据题意,把第十九届省运会在青少年设置的比赛项目的个数看作单位“1”,第二十届省运会在青少年部设置的比赛项目个数预计比十九届多,第二十届省运会在青少年部设置的比赛项目的个数是第十九届的(1+),用第十九届省运会在青少年部设置的比赛项目的个数×(1+),即28×(1+),即可求出第二十届省运会预计在青少年部设置比赛项目的个数。
【详解】
28×(1+)
=28×
=36(个)
答:第二十届省运会预计在青少年部设置36个比赛项目。
【点睛】利用求比一个数多或少几分之几的数是多少的知识进行解答,注意单位“1”确定。
12.78人
【分析】由三个班人数都是54人,甲班男生人数与乙班女生人数同样多,可以判断出甲、乙两班女生人数正好相当于一个班人数即54人;
丙班女生占全班的,即54×=24(人),把54与24相加即可求出三个班女生总数。
【详解】54+54×
=54+24
=78(人)
答:这三个班一共有女生78人。
【点睛】弄清甲、乙两班女生人数总和是解决本题的关键。
13.篮球:120元;排球:96元
【分析】根据题意,设篮球的价格是x元,排球的单价是篮球的,排球的价格=篮球的价格×,排球的价格是x元;买了一个篮球和一个排球一共用去216元,列方程:x+x=216,解方程,即可解答。
【详解】解:设篮球的价格数x元,则排球的价格是x元。
x+x=216
x=216
x=216÷
x=216×
x=120
排球价格:120×=96(元)
答:篮球的价格是120元,排球的价格是96元,
【点睛】本题是方程的实际应用,根据篮球和排球价格的关系,设出未知数,列方程,解方程。
14.男运动员90人;女运动员72人
【分析】根据题意,设女运动员有x人,把女运动员人数看作单位“1”,男运动员比女运动员多,则男运动员有(1+)x人,一共有162人,列方程:x+(1+)x=162,解方程,即可解答。
【详解】解:设女运动员有x人,则男运动员有(1+)x人。
x+(1+)x=162
x+ x=162
x=162
x=162÷
x=162×
x=72
男运动员有:162-72=90(人)
答:男运动员有90人,女运动员有72人。
【点睛】本题考查方程的实际应用,关键是把女运动员的人数看作单位“1”,再根据题意,设出未知数,找出相关的量,列方程,解方程。
15.120页
【分析】根据题意,求出两天看全书的几分之几,用+,再用两天一共看的页数除以两天看全书页数的几分之几,即可解答。
【详解】69÷(+)
=69÷(+)
=69÷
=69×
=120(页)
答:这本书共有120页。
【点睛】本题考查已知一个数的几分之几是多少,求这个数。
16.42个
【分析】根据题意,把甲筐中原有的苹果个数看作单位“1”,卖出,还剩1-,用45×(1-),求出甲筐中还剩苹果个数;这时甲筐剩下的苹果个数等于乙筐卖出剩下的苹果个数;把乙筐中原有苹果个数看作单位“1”,卖出,还剩1-,对应的是甲筐剩下的苹果个数,再用甲筐剩下的苹果个数÷(1-),求出乙筐中原来有苹果个数。
【详解】45×(1-)÷(1-)
=45×÷
=36÷
=36×
=42(个)
答:乙筐中原有苹果42个。
【点睛】本题考查分数四则混合运算,求一个数的几分之几是多少;已知一个数的几分之几是多少,求这个数。
17.84吨
【分析】求出两次一共运走面粉总数的几分之几,用第一次运走总数的+第二次运走总数的,再用两次一共运走的49吨÷(+),即可解答。
【详解】49÷(+)
=49÷(+)
=49÷
=49×
=84(吨)
答:这批面粉一共84吨。
【点睛】本题考查分数的四则混合运算,已知一个数的几分之几是多少,求这个数。
18.不相等
【分析】把冲锋衣的原价看作单位“1”,降价,降价后的价格是原价的(1-),求出降价后的价格,用原价×(1-),即360×(1-)=300元,再把降价后的冲锋衣的价格看作单位“1”,提价,现价就是降价后价格的(1+),再用降价后的价格×(1+),再和原价比较,即可解答。
【详解】360×(1-)×(1+)
=360××
=300×
=350(元)
360元≠350元
答:现在这件冲锋衣的价格和原来不相等。
【点睛】本题考查求一个数的几分之几是多少,关键是找准单位“1”。
19.千克
【分析】先求出前两次用去的质量,即+,再乘,就是第三次用去的质量。
【详解】(+)×
=×
=
=(千克)
答:第三次用去千克。
【点睛】本题考查求一个数的几分之几是多少,用乘法解决。
20.苹果:100元;香蕉:75元
【分析】可以设每筐苹果x元,则每筐香蕉的价钱:x,由于12×每筐苹果的价格+6×每筐香蕉的价格=1650,由此即可列方程,再根据等式的性质解方程即可。
【详解】解:设每筐苹果x元,则每筐香蕉的价钱:x元。
12x+6×x=1650
16.5x=1650
x=1650÷16.5
x=100
100×=75(元)
答:每筐苹果100元,每筐香蕉75元。
【点睛】此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子表示,然后列方程解答。
21.35名
【分析】设初级阶段出席人数为x人,缺席的学生人数占出席人数的,缺席人数为x人;又有一名同学请假,现在出席人数为(x-1)人,缺席人数占出席人数的,缺席人数为(x-1),列方程:x+1=(x-1)×,解方程,进而求出现在出席人数。
【详解】解:设初级出席人数为x人
x+1=(x-1)×
x+1=x-
x-x=1+
x-x=
x=
x=÷
x=×30
x=36
36-1=35(人)
答:现在还有35人。
【点睛】本题考查方程的实际应用,根据题意找出相关的量,列方程,解方程。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末应用题易错专项:分数四则混合运算-数学六年级上册苏教版
1.甲、乙两城相距480千米,一辆汽车上午9:00从甲城开往乙城,4小时行了全程的,照这样计算,这辆汽车在下午三点之前能否到达乙城?
2.家里的菜地共450平方米,王大爷准备用种番茄,按4∶9的面积比种黄瓜与番茄,黄瓜的种植面积是多少平方米?
3.三信小学美术组有63人,比舞蹈组的人数多,舞蹈组有多少人?(列方程解)
4.两筐苹果共重126千克。从第一筐取出放入第二筐,两筐苹果就同样重。原来两筐苹果各重多少千克?
5.勺湖公园想在下图的A、B、C三个景点处各立一块标牌。A、B、C三个景点分别在从进口到出口处的、、处。请你仿照A处标牌上的内容,设计出B、C两处标牌内容并填在牌子上。
6.中国农历中的“夏至”是一年中白昼最长、黑夜最短的一天。去年的“夏至”,某市的黑夜时间比白昼时间少。这天白昼和黑夜分别是多少小时?(先用线段图表示出黑夜的时间,再计算)
7.为了提升课后服务质量,学校特开设魔方课程,学习魔方课程的同学被分为两组,第一小组学习三阶魔方,第二小组学习四阶魔方,第一小组与第二小组人数的比是,如果第一小组调出14人到第二小组学习四阶魔方,这时第一小组与第二小组人数的比是,原来两个小组各有多少人?
8.2021年5月9日上午,在三亚水稻国家公园示范点,袁隆平团队研发的第五期超级杂交水稻“超优于号”开始测产。专家组选取了3个地块,同时进行收割、打谷,汇总后按照高产创建产量公式计算,最终测产结果约为每公顷15吨,比第二期超级杂交水稻的产量增产。第二期超级杂交水稻产量大约是每公顷多少吨?(列方程解答)
9.两个仓库共有空调3000台,如果从甲仓库调出放到乙仓库,那么甲乙两仓库的空调台数的比是2∶3,原来甲仓库有空调多少台?
10.一桶油连桶共重16.5千克,倒出油的后,连桶共重11.5千克,油桶重多少千克?
11.第二十届省运会将于2022年8月28日至9月5日在泰州举行。省运会比赛分为青少年部、高校部和职工部三个部分。第十九届省运会在青少年部设置了28个比赛项目,第二十届省运会在青少年部设置的比赛项目预计比上届多。第二十届省运会预计在青少年部设置多少个比赛项目?(先把线段图补充完整,再解答)
12.某校五年级甲、乙、丙三个班分别都是54人,其中甲班男生人数与乙班女生人数同样多,丙班女生占全班人数的。这三个班一共有女生多少人?
13.刘老师买了一个篮球和一个排球一共用去216元,排球的单价是篮球的。一个排球和一个篮球的价格分别是多少元?
14.学校举办春季运动会,参加比赛的运动员一共有162人。已知男运动员的人数比女运动员多,请你算一算,男、女运动员各有多少人?
15.小明看一本课外书,第一天看了全书的,第二天看了全书的,两天一共看了69页,这本书共有多少页?
16.甲、乙两筐苹果,甲筐中已卖出,乙筐中已卖出,两筐剩下的苹果数量正好相等,已知甲筐中原有苹果45个,乙筐中原有苹果多少个?
17.仓库运一批面粉,第一次运走总数的,第二次运走总数的,两次一共运走了49吨。这批面粉一共多少吨?
18.一件冲锋衣的原价是360元,在国庆促销活动中降价,活动结束后又提价。现在这件冲锋衣的价格和原来相等吗?
19.一桶油,第一次用去千克,第二次用去千克,第三次用去前两次总质量的。第三次用去多少千克?
20.水果店有12筐苹果和6筐香蕉,一共需1650元,每筐香蕉的价钱是苹果的。每筐苹果多少元?每筐香蕉多少元?
21.学校举行运动会,缺席的学生人数占出席学生人数的,后来又有一个学生请假回家,这时缺席学生人数占出席学生人数的。求现在还有多少学生。
参考答案:
1.不能
【分析】用480×,求出汽车4小时行驶的路程。再根据速度=路程÷时间,代入数据,求出汽车的速度,再根据时间=路程÷速度,求出甲城到乙城的时间,进而解答。
【详解】480÷(480×÷4)
=480÷(320÷4)
=480÷80
=6(小时)
上午9:00=9时
9时+6小时=15时=下午3时。下午三点之前不能到达乙城。
答:这辆汽车在下午三点之前不能到达乙城。
【点睛】根据速度、时间、路程三者关系已经求一个数的几分之几是多少的计算方法进行解答。
2.60平方米
【分析】把这块菜地的面积看作单位“1” 王大爷准备用种番茄,用这块地的面积× ,求出种番茄的面积;按4∶9的面积种黄瓜与番茄,把种黄瓜和番茄的面积分成4+9份,番茄占其中的9,即番茄占种番茄和黄瓜的,黄瓜占种番茄和黄瓜面积的,用种番茄的面积÷,求出种番茄和黄瓜的面积,再进一步求出种黄瓜的面积。
【详解】450×÷×
=135÷×
=135××
=195×
=60(平方米)
答:黄瓜的种植面积是60平方米。
【点睛】利用求一个数的几分之几的计算方法,已知一个数的几分之几是多少,求这个数的计算方法以及按比例分配的计算方法进行解答。
3.56人
【分析】把舞蹈组的人数看作单位“1”,美术小组的人数比舞蹈组的人数多,美术小组的人数是舞蹈组的(1+),用舞蹈组的人数×(1+)=美术组的人数,设舞蹈组有x人,列方程:x×(1+)=63,解方程,即可解答。
【详解】解:设舞蹈组有x人。
x×(1+)=63
x=63
x=63÷
x=63×
x=56
答:舞蹈组有56人。
【点睛】本题考查方程的实际应用,根据求比一个数多或少几分之几的数是多少的计算方法,设出未知数,找出相关的量,列方程,解方程。
4.第一筐重81千克;第二筐重45千克
【分析】从第一筐取出放入第二筐,两筐苹果就同样重,则现在每筐苹果的重量是126÷2=63(千克)。把原来第一筐苹果的重量看作单位“1”,取出后,现在的重量是原来重量的(1-),根据“已知一个数的几分之几是多少,求这个数,用除法计算”,用63除以(1-)即可求出原来第一筐苹果的重量。再用126减去原来第一筐的重量求出原来第二筐苹果的重量。
【详解】126÷2=63(千克)
第一筐:63÷(1-)
=63÷
=63×
=81(千克)
第二筐:126-81=45(千克)
答:原来第一筐苹果重81千克,第二筐重45千克。
【点睛】本题考查分数四则混合运算的应用。已知一个数的几分之几是多少,求这个数,用除法计算,据此先求出第一筐苹果现在的重量,以及现在的重量是原来重量的几分之几是解题的关键。
5.见详解
【分析】把进口与出口之间的距离看作单位“1”,A、B、C三个景点处各立一块标牌。A、B、C三个景点分别在从进口到出口处的、、,由此可知A景点距离出口2.5千米占进口与出口距离的(1-),用2.5÷(1-),求出进口与出口的距离;再用进口与出口的距离×(1-);进口与出口的距离×(1-),分别求出B、C各距离进口的距离,据此解答。
【详解】2.5÷(1-)
=2.5÷
=2.5×
=(千米)
×(1-)
=×
=2(千米)
×(1-)
=×
=1(千米)
所以B景点距离出口2千米,C景点距离出口1千米。
【点睛】解答本题的关键是单位“1”的确定,重点是求出进口与出口之间的距离,进而求出B景点距离出口多少千米,C景点距离出口多少千米。
6.图见详解
白昼:14小时;黑夜:10小时
【分析】把白昼时间看作单位“1”,根据题中的已知条件,白昼平均分成7段,黑夜比白昼少2段,则用线段画5段表示出黑夜的时间;把白昼的时间看作单位“1”,则黑夜的时间是白昼时间的(1-),用白昼时间×(1-),就是黑夜的时间,设白昼时间为x小时,则黑夜时间为(1-)x小时;白昼+黑夜=24小时,列方程:x+(1-)x=24,解方程,求出白昼的时间,进而求出黑夜的时间。
【详解】
解:设白昼的时间为x小时,则黑夜时间为(1-)x小时。
x+(1-)x=24
x+x=24
x=24
x=24÷
x=24×
x=14
24-14=10(小时)
答:白昼时间是14小时,黑夜时间是10小时。
【点睛】本题考查方程的实际应用。可以白昼与黑夜的时间关系,设出未知数,找出相关的量,列方程,解方程,注意一天是24小时,即白昼+黑夜=小时。
7.第一小组:30人;第二小组:18人
【分析】根据题意,把两个小组的总人数看作单位“1”,第二小组的人数原来占总人数的,现在第二小组的人数占总人数的,增加了总人数的(-),对应的是14人,用14÷(-),求出两个小组的总人数,进而求出原来各自小组有的人数。
【详解】14÷(-)
=14÷(-)
=14÷(-)
=14÷
=14×
=48(人)
第二小组:48×
=48×
=18(人)
第一小组:48-18=30(人)
答:原来第一小组有30人,第二小组有18人。
【点睛】本题主要找出不变的量作为单位“1”,求出14人所对应的分率,进而进行解答。
8.12吨
【分析】设第二期超级杂交水稻产量大约是每公顷x吨,则(1+)x等于15吨,列方程:(1+)x=15,解方程,即可解答。
【详解】解:设第二期超级杂交水稻产量大约是每公顷x吨。
(1+)x=15
x=15
x=15÷
x=15×
x=12
答:第二期超级杂交水稻产量大约是每公顷12吨。
【点睛】本题考查方程的实际应用,关键是找准题目中的等量关系。
9.1600台
【分析】两个仓库共有空调3000台,后来甲仓库与乙仓库的存空调台数数比是2∶3,一共是2+3=5份,先用3000台除以5份,求出每份的台数,进而分别求出甲仓后来的台数,甲仓后来的台数相当于原来的台数的(1-),据分数除法的意义求出甲仓库原来的台数。
【详解】3000÷(2+3)×2÷(1-)
=3000÷5×2÷
=1200÷
=1600(台)
答:原来甲仓库有1600台空调。
【点睛】解答此题的关键是明确:从甲仓库取出到乙仓库,甲、乙两个仓库的空调台数的和不变,再根据两者后来的比,按照按比分配的方法,分别求出它们后来的台数,再逆推出原来的台数。
10.1.5千克
【分析】用16.5-11.5,求出倒出油的重量,把这桶油的重量看作单位“1”,倒出油的,对应的是倒出油的重量,用倒出油的重量除以,求出这桶油的重量,再用这桶油连桶的重量-这桶油的重量,即可求出油桶的重量。
【详解】16.5-(16.5-11.5)÷
=16.5-5÷
=16.5-5×3
=16.5-15
=1.5(千克)
答:油桶重1.5千克。
【点睛】利用已知一个数的几分之几是多少,求这个数的知识进行解答,关键是求出倒出油的对应的油的重量。
11.图见详解;36个
【分析】根据题意,把第十九届省运会在青少年设置的比赛项目的个数看作单位“1”,第二十届省运会在青少年部设置的比赛项目个数预计比十九届多,第二十届省运会在青少年部设置的比赛项目的个数是第十九届的(1+),用第十九届省运会在青少年部设置的比赛项目的个数×(1+),即28×(1+),即可求出第二十届省运会预计在青少年部设置比赛项目的个数。
【详解】
28×(1+)
=28×
=36(个)
答:第二十届省运会预计在青少年部设置36个比赛项目。
【点睛】利用求比一个数多或少几分之几的数是多少的知识进行解答,注意单位“1”确定。
12.78人
【分析】由三个班人数都是54人,甲班男生人数与乙班女生人数同样多,可以判断出甲、乙两班女生人数正好相当于一个班人数即54人;
丙班女生占全班的,即54×=24(人),把54与24相加即可求出三个班女生总数。
【详解】54+54×
=54+24
=78(人)
答:这三个班一共有女生78人。
【点睛】弄清甲、乙两班女生人数总和是解决本题的关键。
13.篮球:120元;排球:96元
【分析】根据题意,设篮球的价格是x元,排球的单价是篮球的,排球的价格=篮球的价格×,排球的价格是x元;买了一个篮球和一个排球一共用去216元,列方程:x+x=216,解方程,即可解答。
【详解】解:设篮球的价格数x元,则排球的价格是x元。
x+x=216
x=216
x=216÷
x=216×
x=120
排球价格:120×=96(元)
答:篮球的价格是120元,排球的价格是96元,
【点睛】本题是方程的实际应用,根据篮球和排球价格的关系,设出未知数,列方程,解方程。
14.男运动员90人;女运动员72人
【分析】根据题意,设女运动员有x人,把女运动员人数看作单位“1”,男运动员比女运动员多,则男运动员有(1+)x人,一共有162人,列方程:x+(1+)x=162,解方程,即可解答。
【详解】解:设女运动员有x人,则男运动员有(1+)x人。
x+(1+)x=162
x+ x=162
x=162
x=162÷
x=162×
x=72
男运动员有:162-72=90(人)
答:男运动员有90人,女运动员有72人。
【点睛】本题考查方程的实际应用,关键是把女运动员的人数看作单位“1”,再根据题意,设出未知数,找出相关的量,列方程,解方程。
15.120页
【分析】根据题意,求出两天看全书的几分之几,用+,再用两天一共看的页数除以两天看全书页数的几分之几,即可解答。
【详解】69÷(+)
=69÷(+)
=69÷
=69×
=120(页)
答:这本书共有120页。
【点睛】本题考查已知一个数的几分之几是多少,求这个数。
16.42个
【分析】根据题意,把甲筐中原有的苹果个数看作单位“1”,卖出,还剩1-,用45×(1-),求出甲筐中还剩苹果个数;这时甲筐剩下的苹果个数等于乙筐卖出剩下的苹果个数;把乙筐中原有苹果个数看作单位“1”,卖出,还剩1-,对应的是甲筐剩下的苹果个数,再用甲筐剩下的苹果个数÷(1-),求出乙筐中原来有苹果个数。
【详解】45×(1-)÷(1-)
=45×÷
=36÷
=36×
=42(个)
答:乙筐中原有苹果42个。
【点睛】本题考查分数四则混合运算,求一个数的几分之几是多少;已知一个数的几分之几是多少,求这个数。
17.84吨
【分析】求出两次一共运走面粉总数的几分之几,用第一次运走总数的+第二次运走总数的,再用两次一共运走的49吨÷(+),即可解答。
【详解】49÷(+)
=49÷(+)
=49÷
=49×
=84(吨)
答:这批面粉一共84吨。
【点睛】本题考查分数的四则混合运算,已知一个数的几分之几是多少,求这个数。
18.不相等
【分析】把冲锋衣的原价看作单位“1”,降价,降价后的价格是原价的(1-),求出降价后的价格,用原价×(1-),即360×(1-)=300元,再把降价后的冲锋衣的价格看作单位“1”,提价,现价就是降价后价格的(1+),再用降价后的价格×(1+),再和原价比较,即可解答。
【详解】360×(1-)×(1+)
=360××
=300×
=350(元)
360元≠350元
答:现在这件冲锋衣的价格和原来不相等。
【点睛】本题考查求一个数的几分之几是多少,关键是找准单位“1”。
19.千克
【分析】先求出前两次用去的质量,即+,再乘,就是第三次用去的质量。
【详解】(+)×
=×
=
=(千克)
答:第三次用去千克。
【点睛】本题考查求一个数的几分之几是多少,用乘法解决。
20.苹果:100元;香蕉:75元
【分析】可以设每筐苹果x元,则每筐香蕉的价钱:x,由于12×每筐苹果的价格+6×每筐香蕉的价格=1650,由此即可列方程,再根据等式的性质解方程即可。
【详解】解:设每筐苹果x元,则每筐香蕉的价钱:x元。
12x+6×x=1650
16.5x=1650
x=1650÷16.5
x=100
100×=75(元)
答:每筐苹果100元,每筐香蕉75元。
【点睛】此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子表示,然后列方程解答。
21.35名
【分析】设初级阶段出席人数为x人,缺席的学生人数占出席人数的,缺席人数为x人;又有一名同学请假,现在出席人数为(x-1)人,缺席人数占出席人数的,缺席人数为(x-1),列方程:x+1=(x-1)×,解方程,进而求出现在出席人数。
【详解】解:设初级出席人数为x人
x+1=(x-1)×
x+1=x-
x-x=1+
x-x=
x=
x=÷
x=×30
x=36
36-1=35(人)
答:现在还有35人。
【点睛】本题考查方程的实际应用,根据题意找出相关的量,列方程,解方程。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
