4.3.1 一元线性回归模型 第1课时 课件(共25张PPT)
文档属性
| 名称 | 4.3.1 一元线性回归模型 第1课时 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 07:31:42 | ||
图片预览








文档简介
(共25张PPT)
4.3.1 一元线性回归模型
第1课时
新授课
1.结合实例,了解两个变量之间的相关关系的含义,知道线性相关关系及正相关、负相关、散点图等概念.
2.结合具体实例,了解一元线性回归模型的概念及最小二乘法原理,掌握回归直线方程的求法.
3.结合直线方程的性质,了解回归直线方程的性质及了解模型参数的统计意义,会用回归模型对实际问题进行预测.
你知道“名师出高徒”的意思吗?
——高明的师傅一定能教出技艺高的徒弟,比喻学识丰富的人对于培养人才的重要.也就是说,高水平的老师往往能教出高水平的学生.
那么老师的水平与学生的水平之间具有怎样的关系呢?这种关系是确定的吗?该关系与函数关系相同吗?
情境与问题
(1)圆的面积S与半径r之间的关系;
(2)16岁学生的体重w与身高h之间的关系;
(3)匀速运动的物体,其运动的路程S与时间t之间的关系;
(4)学习成绩 f 与平均学习时间t之间的关系.
S=πr2
S=vt
思考:分析以上变量之间的关系,它们可按什么标准分为两类,每一类变量关系有何特点?
知识点一:变量的相关关系及线性相关
1.具有确定性:如(1)(3)是明确的函数关系.
2.有一定关系,但不能互相确定:如(2)(4)不具有明确的函数关系.
分类
概念生成
如果两个变量之间有一定的关系,但没有达到可以互相决定的程度,它们之间的关系具有一定的随机性,像这样两个变量之间的关系,统计学上都称为相关关系.
相关关系
数学 88 82 79 89 92 78 79 56 83 66 61 74 68 77 78 80
物理 87 91 66 86 88 79 91 53 93 77 62 69 62 58 79 68
数学 51 58 98 73 75 84 69 76 71 43 74 82 70 75 65 63
物理 50 65 82 79 59 98 59 87 76 42 75 91 46 68 83 55
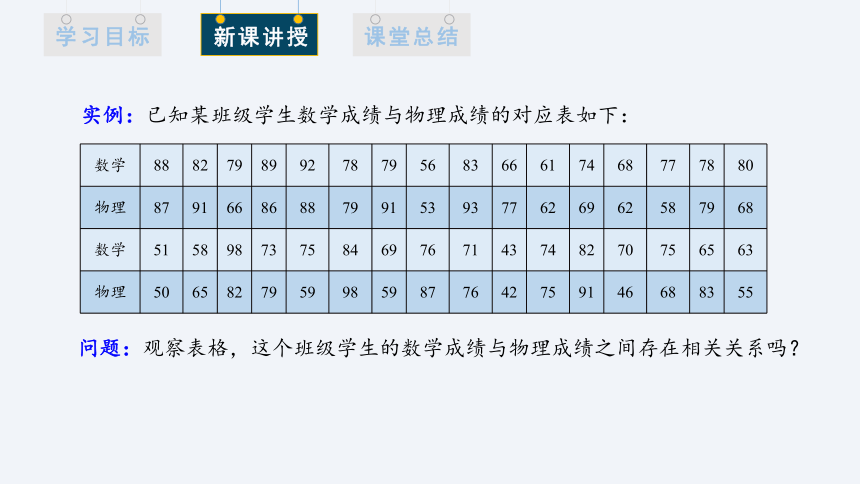
实例:已知某班级学生数学成绩与物理成绩的对应表如下:
问题:观察表格,这个班级学生的数学成绩与物理成绩之间存在相关关系吗?
数学 43 51 56 58 61 63 65 66 68 69 70 71 73 74 74 75
物理 42 50 53 65 66 55 83 77 62 59 46 76 79 69 75 59
数学 75 76 77 78 78 79 79 80 82 82 83 84 88 89 92 98
物理 68 87 58 79 79 66 91 68 91 91 93 98 87 86 88 82
由表可知:数学成绩增加时,物理成绩大致也增加.
①对数据进行如下整理:
②根据表格数据作如下图像.
散点图
该班级学生数学成绩与物理成绩构成的点分布在直线上或直线的两侧,且都在直线附近.
因此数学成绩与物理成绩之间有相关关系的,可以近似用一次函数来描述它们之间的关系.
由图可得:
数学成绩增加时,物理成绩大致也增加.
如果由变量的成对数据、散点图或直观经验可知,变量x与变量y之间的关系可以近似地用一次函数来刻画,则称x与y线性相关.
线性相关关系
概念生成
如果一个变量增大,另一个变量大体上也增大,则称这两个变量正相关.
如果一个变量增大,另一个变量大体上减少,则称这两个变量负相关.
·
·
·
·
·
·
·
·
·
·
·
·
y
x
o
正相关
·
·
·
·
·
·
·
·
·
·
·
y
x
o
负相关
某公司的利润y(单位:千万元)与销售总额x(单位:千万元)之间有如下表对应数据:
(1)画出散点图;
(2)判断y与x是否具有线性相关关系.
x 10 15 17 20 25 28 32
y 1 1.3 1.8 2 2.6 2.7 3.3
解:(1)散点图如右图所示:
(2)由图可知,所有数据点接近直线排列,
因此,y与x有线性相关关系,且为正相关.
练一练
某地区从某一年开始进行了环境污染整治,得到了如下数据
第x年 1 2 3 4 5 6 7
污染指数y 6.1 5.2 4.5 4.7 3.8 3.4 3.1
(1)作出这些成对数据的散点图,则污染指数y与x是否线性相关?如果是,判断是正相关还是负相关.
知识点二:回归直线方程
y与x是具有线性相关关系,且为负相关.
(2)如何找出近似描述y与x之间关系的一次函数表达式?
例如:过点(1,6)和(7,3),得 y=-0.5x+6.5.
y=-0.5x+6.5是最好的直线吗?衡量标准是什么呢?
过点(1,6)和(6,3.4),得
y=-0.54x+6.52.
......
第x年 1 2 3 4 5 6 7
污染指数y 6.1 5.2 4.5 4.7 3.8 3.4 3.1
预测值-0.5x+6.5
误差(残差)
6
5.5
4.5
5
4
3
0.1
-0.3
-0.5
0.2
-0.2
-0.1
0.1
3.5
由函数表达式y=-0.5x+6.5可得下表:
“最好”的直线
误差平方和最小.
y关于x的回归直线方程
.
误差平方和最小的直线为:
可以证明,对于表格数据
取得最小值,
则 称为y关于x的回归直线方程(对应的直线称为回归直线).
概念生成
一般地,已知变量x与y的n对成对数据(xi,yi),i=1,2,3,…,n.任意给定一个一次函数y=bx+a,对每一个已知的xi,由直线方程可以得到一个估计值
最小二乘法.
方法
如果一次函数 能使残差平方和即
回归直线方程
最小二乘法确定回归直线方程
给定两个变量y与x的一组数据之后,回归直线方程 总是存在的,
其中称为回归系数.它实际上也就是回归直线方程的斜率.
而且
思考:某地区从某一年开始进行了环境污染整治,得到了如下数据
第x年 1 2 3 4 5 6 7
污染指数y 6.1 5.2 4.5 4.7 3.8 3.4 3.1
已知y与x线性相关,求近似描述y与x之间关系的一次函数表达式,该地区第8年的污染指数估计为多少?
由表中所给数据可得 ,可得下表:
因此
所求的y关于x的线性回归直线方程为
由题意,将x=8代入回归方程 ,可得
所以预测第8年的污染指数为2.5.
思考:假设y与x具有相关关系,而且回归直线方程为+,
(1)将=代入回归直线方程,并求出
将 = 代入 +,可得 即:回归直线一定过(,).
一次函数 + 的单调性由决定.
即:y与x正相关的充要条件;y与x负相关的充要条件
(2)一次函数 + 的单调性由谁决定?函数的单调性与正相关、负相关之间有怎样的联系?
知识点三:回归直线方程的性质.
(3)当x每增大一个单位时, 将如何变化
?
由直线方程的性质可知,
归纳总结
①回归直线一定过(,).
② y与x正相关的充要条件;
y与x负相关的充要条件
③
回归直线方程
的性质:
例1 如果某位同学10次考试的物理成绩y与数学成绩x如下表所示.
数学成绩x 76 82 72 87 93 78 89 66 81 76
物理成绩y 80 87 75 86 100 79 93 68 85 77
已知y与x线性相关:(1)判断正相关还是负相关;
解:(1)根据数据可作出散点图,如图所示
从图上可以直观地看出,y与x正相关.
(2)求出y关于x的回归直线方程;
将每个x的值都减去80可得-4,2,-8,7,13,-2,9,-14,1,-4.
这些数字的平均数为0,因此=80.
将每个y的值都减去80可得0,7,-5,6,20,-1,13,-12,5,-3.
这些数字的平均数为3,因此=83.
数学成绩x 76 82 72 87 93 78 89 66 81 76
物理成绩y 80 87 75 86 100 79 93 68 85 77
因此
回归直线方程为
(3)该同学的数学成绩每提高3分,物理成绩估计能提高多少分?
由回归系数 可知,x每增大1个单位时, 增大1.1个单位.
因此,数学成绩每提高3分,物理成绩估计能提高的分值为
1.1×3=3.3.
求线性回归方程的步骤:(1)画出散点图.从直观上分析数据间是否存在线性相关关系.(2)计算 等相关数据.(3)代入公式求出 中参数 的值.(4)写出回归方程并对实际问题作出估计.
归纳总结
根据本节课所学,回答下列问题:
1.线性相关关系可以分为哪几类?
2.用什么方法求回归直线方程中,,公式是什么?
3.求回归直线方程的步骤是什么?
4.3.1 一元线性回归模型
第1课时
新授课
1.结合实例,了解两个变量之间的相关关系的含义,知道线性相关关系及正相关、负相关、散点图等概念.
2.结合具体实例,了解一元线性回归模型的概念及最小二乘法原理,掌握回归直线方程的求法.
3.结合直线方程的性质,了解回归直线方程的性质及了解模型参数的统计意义,会用回归模型对实际问题进行预测.
你知道“名师出高徒”的意思吗?
——高明的师傅一定能教出技艺高的徒弟,比喻学识丰富的人对于培养人才的重要.也就是说,高水平的老师往往能教出高水平的学生.
那么老师的水平与学生的水平之间具有怎样的关系呢?这种关系是确定的吗?该关系与函数关系相同吗?
情境与问题
(1)圆的面积S与半径r之间的关系;
(2)16岁学生的体重w与身高h之间的关系;
(3)匀速运动的物体,其运动的路程S与时间t之间的关系;
(4)学习成绩 f 与平均学习时间t之间的关系.
S=πr2
S=vt
思考:分析以上变量之间的关系,它们可按什么标准分为两类,每一类变量关系有何特点?
知识点一:变量的相关关系及线性相关
1.具有确定性:如(1)(3)是明确的函数关系.
2.有一定关系,但不能互相确定:如(2)(4)不具有明确的函数关系.
分类
概念生成
如果两个变量之间有一定的关系,但没有达到可以互相决定的程度,它们之间的关系具有一定的随机性,像这样两个变量之间的关系,统计学上都称为相关关系.
相关关系
数学 88 82 79 89 92 78 79 56 83 66 61 74 68 77 78 80
物理 87 91 66 86 88 79 91 53 93 77 62 69 62 58 79 68
数学 51 58 98 73 75 84 69 76 71 43 74 82 70 75 65 63
物理 50 65 82 79 59 98 59 87 76 42 75 91 46 68 83 55
实例:已知某班级学生数学成绩与物理成绩的对应表如下:
问题:观察表格,这个班级学生的数学成绩与物理成绩之间存在相关关系吗?
数学 43 51 56 58 61 63 65 66 68 69 70 71 73 74 74 75
物理 42 50 53 65 66 55 83 77 62 59 46 76 79 69 75 59
数学 75 76 77 78 78 79 79 80 82 82 83 84 88 89 92 98
物理 68 87 58 79 79 66 91 68 91 91 93 98 87 86 88 82
由表可知:数学成绩增加时,物理成绩大致也增加.
①对数据进行如下整理:
②根据表格数据作如下图像.
散点图
该班级学生数学成绩与物理成绩构成的点分布在直线上或直线的两侧,且都在直线附近.
因此数学成绩与物理成绩之间有相关关系的,可以近似用一次函数来描述它们之间的关系.
由图可得:
数学成绩增加时,物理成绩大致也增加.
如果由变量的成对数据、散点图或直观经验可知,变量x与变量y之间的关系可以近似地用一次函数来刻画,则称x与y线性相关.
线性相关关系
概念生成
如果一个变量增大,另一个变量大体上也增大,则称这两个变量正相关.
如果一个变量增大,另一个变量大体上减少,则称这两个变量负相关.
·
·
·
·
·
·
·
·
·
·
·
·
y
x
o
正相关
·
·
·
·
·
·
·
·
·
·
·
y
x
o
负相关
某公司的利润y(单位:千万元)与销售总额x(单位:千万元)之间有如下表对应数据:
(1)画出散点图;
(2)判断y与x是否具有线性相关关系.
x 10 15 17 20 25 28 32
y 1 1.3 1.8 2 2.6 2.7 3.3
解:(1)散点图如右图所示:
(2)由图可知,所有数据点接近直线排列,
因此,y与x有线性相关关系,且为正相关.
练一练
某地区从某一年开始进行了环境污染整治,得到了如下数据
第x年 1 2 3 4 5 6 7
污染指数y 6.1 5.2 4.5 4.7 3.8 3.4 3.1
(1)作出这些成对数据的散点图,则污染指数y与x是否线性相关?如果是,判断是正相关还是负相关.
知识点二:回归直线方程
y与x是具有线性相关关系,且为负相关.
(2)如何找出近似描述y与x之间关系的一次函数表达式?
例如:过点(1,6)和(7,3),得 y=-0.5x+6.5.
y=-0.5x+6.5是最好的直线吗?衡量标准是什么呢?
过点(1,6)和(6,3.4),得
y=-0.54x+6.52.
......
第x年 1 2 3 4 5 6 7
污染指数y 6.1 5.2 4.5 4.7 3.8 3.4 3.1
预测值-0.5x+6.5
误差(残差)
6
5.5
4.5
5
4
3
0.1
-0.3
-0.5
0.2
-0.2
-0.1
0.1
3.5
由函数表达式y=-0.5x+6.5可得下表:
“最好”的直线
误差平方和最小.
y关于x的回归直线方程
.
误差平方和最小的直线为:
可以证明,对于表格数据
取得最小值,
则 称为y关于x的回归直线方程(对应的直线称为回归直线).
概念生成
一般地,已知变量x与y的n对成对数据(xi,yi),i=1,2,3,…,n.任意给定一个一次函数y=bx+a,对每一个已知的xi,由直线方程可以得到一个估计值
最小二乘法.
方法
如果一次函数 能使残差平方和即
回归直线方程
最小二乘法确定回归直线方程
给定两个变量y与x的一组数据之后,回归直线方程 总是存在的,
其中称为回归系数.它实际上也就是回归直线方程的斜率.
而且
思考:某地区从某一年开始进行了环境污染整治,得到了如下数据
第x年 1 2 3 4 5 6 7
污染指数y 6.1 5.2 4.5 4.7 3.8 3.4 3.1
已知y与x线性相关,求近似描述y与x之间关系的一次函数表达式,该地区第8年的污染指数估计为多少?
由表中所给数据可得 ,可得下表:
因此
所求的y关于x的线性回归直线方程为
由题意,将x=8代入回归方程 ,可得
所以预测第8年的污染指数为2.5.
思考:假设y与x具有相关关系,而且回归直线方程为+,
(1)将=代入回归直线方程,并求出
将 = 代入 +,可得 即:回归直线一定过(,).
一次函数 + 的单调性由决定.
即:y与x正相关的充要条件;y与x负相关的充要条件
(2)一次函数 + 的单调性由谁决定?函数的单调性与正相关、负相关之间有怎样的联系?
知识点三:回归直线方程的性质.
(3)当x每增大一个单位时, 将如何变化
?
由直线方程的性质可知,
归纳总结
①回归直线一定过(,).
② y与x正相关的充要条件;
y与x负相关的充要条件
③
回归直线方程
的性质:
例1 如果某位同学10次考试的物理成绩y与数学成绩x如下表所示.
数学成绩x 76 82 72 87 93 78 89 66 81 76
物理成绩y 80 87 75 86 100 79 93 68 85 77
已知y与x线性相关:(1)判断正相关还是负相关;
解:(1)根据数据可作出散点图,如图所示
从图上可以直观地看出,y与x正相关.
(2)求出y关于x的回归直线方程;
将每个x的值都减去80可得-4,2,-8,7,13,-2,9,-14,1,-4.
这些数字的平均数为0,因此=80.
将每个y的值都减去80可得0,7,-5,6,20,-1,13,-12,5,-3.
这些数字的平均数为3,因此=83.
数学成绩x 76 82 72 87 93 78 89 66 81 76
物理成绩y 80 87 75 86 100 79 93 68 85 77
因此
回归直线方程为
(3)该同学的数学成绩每提高3分,物理成绩估计能提高多少分?
由回归系数 可知,x每增大1个单位时, 增大1.1个单位.
因此,数学成绩每提高3分,物理成绩估计能提高的分值为
1.1×3=3.3.
求线性回归方程的步骤:(1)画出散点图.从直观上分析数据间是否存在线性相关关系.(2)计算 等相关数据.(3)代入公式求出 中参数 的值.(4)写出回归方程并对实际问题作出估计.
归纳总结
根据本节课所学,回答下列问题:
1.线性相关关系可以分为哪几类?
2.用什么方法求回归直线方程中,,公式是什么?
3.求回归直线方程的步骤是什么?
