2.1 坐标法 课件(共15张PPT)
文档属性
| 名称 | 2.1 坐标法 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
2.1 坐标法
新授课
1.掌握平面直角坐标系中两点间的距离公式和中点坐标公式.
2.掌握用坐标法解决几何问题的基本步骤,会用坐标法解决问题.
表示为 x2-x1.
知识点一:两点间距离公式和中点坐标公式
1.若A,B两点在数轴上,其中A,B的坐标分别为x1,x2,如图所示
(1)的坐标如何表示?
|AB|=||=|x2-x1|.
(2)A,B两点间距离可以如何表示?
(3)如果M(x)是线段AB的中点,则=,则数轴上的M坐标如何表示?
M(x)
数轴上的中点坐标公式
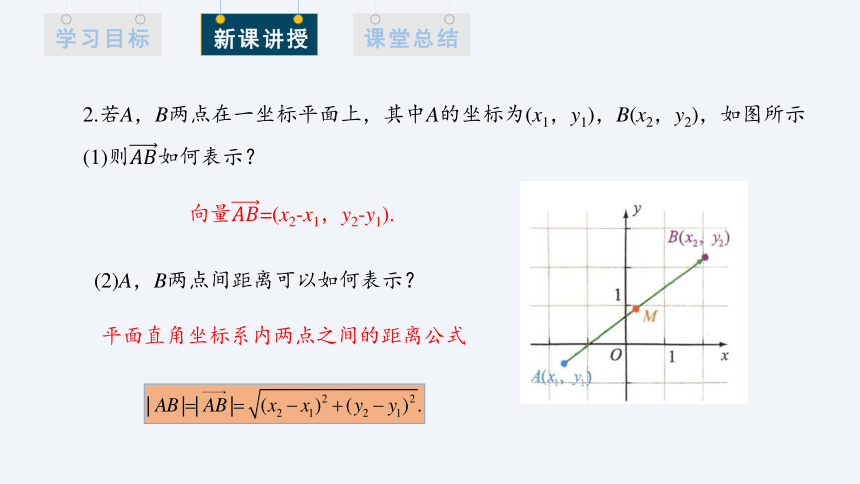
2.若A,B两点在一坐标平面上,其中A的坐标为(x1,y1),B(x2,y2),如图所示
(1)则如何表示?
向量=(x2-x1,y2-y1).
平面直角坐标系内两点之间的距离公式
(2)A,B两点间距离可以如何表示?
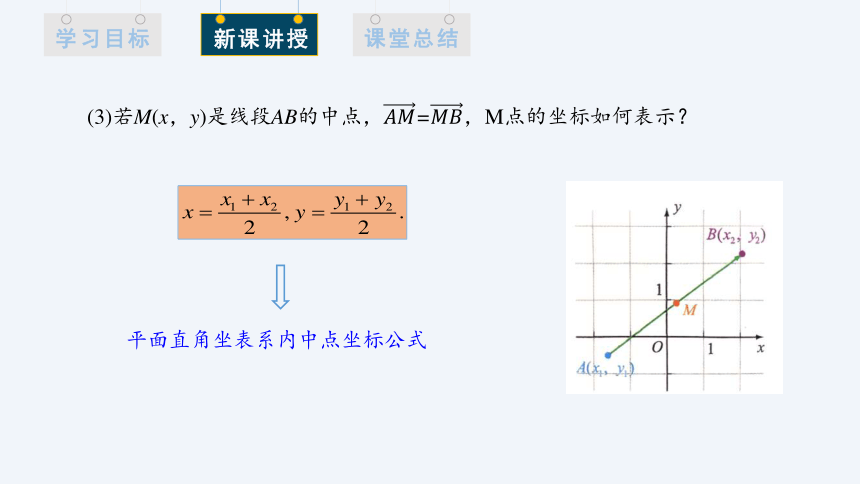
(3)若M(x,y)是线段AB的中点,=,M点的坐标如何表示?
平面直角坐表系内中点坐标公式
例1 已知A(1,2),B(3,4),C(5,0)是△ABC的三个顶点,求这个三角形AB边上中线的长.
解:设AB的中点为M(x,y),则
从而可知所求中线长为
△ABC的顶点A(3,7),B(-2,5),若AC的中点在x轴上,BC的中点在y轴上,求顶点C的坐标.
解:设顶点C的坐标为(x,y),则
∴顶点C的坐标为(-2,7).
练一练
知识点二:坐标法
思考:(1)如图所示 ABCD中,AC,BD的长可以如何表示?
取A为坐标原点,AB所在的直线为x轴,建立如图所示的平面直角坐标系.
则A(0,0),设B(a,0),C(b,c),从而由平行四边形的性质可知D(b-a,c).
因此
A
B
C
D
O
y
x
所以
(2)如何证明 AC2+BD2=2(AB2+AD2)?
由(1)得:
A
B
C
D
O
y
x
通过建立平面直角坐标系,将几何问题转化为代数问题,然后通过代数运算等解决了问题.这种解决问题的方法称为坐标法.
几何问题
几何结论
几何问题
代数问题
建系
反推
坐标法的基本思路:
1.用坐标法解决几何问题的基本步骤:
建系
设点
列式
化简
证明
还原为几何结论
归纳总结
2.建立坐标系应遵循的原则:
(1)尽可能多的已知点落在坐标轴上;
(2)若图形中有互相垂直的两条线,考虑将其作为坐标轴;
(3)若图形具有中心对称性,考虑将图形中心作为坐标原点;
(4)若图形具有对称性,考虑将对称轴作为坐标轴.
例2 已知ABCD是一个长方形,AB=4,AD=1.判断线段CD上是否存在点P,
使得AP⊥BP.如果存在,指出满足条件的P有多少个;如果不存在,说明理由.
解:以AB的中点为原点,AB所在直线为x轴,建立如图所示平面直角坐标系.
设P(t,1)是线段CD上一点,则-2≤t≤2,
因为AP⊥BP的充要条件是⊥,即·=0,即
解得t=或t=-,所以满足条件的P点存在,而且有两个.
(-2-t)(2-t)+1=0.
A(-2,0),B(2,0),C(2,1),D(-2,1).
由题可得
=(-2-t,-1),=(2-t,-1).
而且
练一练
已知△ABC是直角三角形,斜边BC的中点为M,证明:|AM|=|BC|.
证明:如图所示,以Rt△ABC的直角边AB,AC所在直线为坐标轴,
建立平面直角坐标系.设B,C两点的坐标分别为(b,0),(0,c).
因为点M是BC的中点,所以点M的坐标为
所以
C
A
B
M
根据本节课所学回答下列问题:
(1)平面直角坐标系中两点间距离和中点坐标如何求?
(2)用坐标法解决问题时,建立坐标系应遵循哪些原则?
2.1 坐标法
新授课
1.掌握平面直角坐标系中两点间的距离公式和中点坐标公式.
2.掌握用坐标法解决几何问题的基本步骤,会用坐标法解决问题.
表示为 x2-x1.
知识点一:两点间距离公式和中点坐标公式
1.若A,B两点在数轴上,其中A,B的坐标分别为x1,x2,如图所示
(1)的坐标如何表示?
|AB|=||=|x2-x1|.
(2)A,B两点间距离可以如何表示?
(3)如果M(x)是线段AB的中点,则=,则数轴上的M坐标如何表示?
M(x)
数轴上的中点坐标公式
2.若A,B两点在一坐标平面上,其中A的坐标为(x1,y1),B(x2,y2),如图所示
(1)则如何表示?
向量=(x2-x1,y2-y1).
平面直角坐标系内两点之间的距离公式
(2)A,B两点间距离可以如何表示?
(3)若M(x,y)是线段AB的中点,=,M点的坐标如何表示?
平面直角坐表系内中点坐标公式
例1 已知A(1,2),B(3,4),C(5,0)是△ABC的三个顶点,求这个三角形AB边上中线的长.
解:设AB的中点为M(x,y),则
从而可知所求中线长为
△ABC的顶点A(3,7),B(-2,5),若AC的中点在x轴上,BC的中点在y轴上,求顶点C的坐标.
解:设顶点C的坐标为(x,y),则
∴顶点C的坐标为(-2,7).
练一练
知识点二:坐标法
思考:(1)如图所示 ABCD中,AC,BD的长可以如何表示?
取A为坐标原点,AB所在的直线为x轴,建立如图所示的平面直角坐标系.
则A(0,0),设B(a,0),C(b,c),从而由平行四边形的性质可知D(b-a,c).
因此
A
B
C
D
O
y
x
所以
(2)如何证明 AC2+BD2=2(AB2+AD2)?
由(1)得:
A
B
C
D
O
y
x
通过建立平面直角坐标系,将几何问题转化为代数问题,然后通过代数运算等解决了问题.这种解决问题的方法称为坐标法.
几何问题
几何结论
几何问题
代数问题
建系
反推
坐标法的基本思路:
1.用坐标法解决几何问题的基本步骤:
建系
设点
列式
化简
证明
还原为几何结论
归纳总结
2.建立坐标系应遵循的原则:
(1)尽可能多的已知点落在坐标轴上;
(2)若图形中有互相垂直的两条线,考虑将其作为坐标轴;
(3)若图形具有中心对称性,考虑将图形中心作为坐标原点;
(4)若图形具有对称性,考虑将对称轴作为坐标轴.
例2 已知ABCD是一个长方形,AB=4,AD=1.判断线段CD上是否存在点P,
使得AP⊥BP.如果存在,指出满足条件的P有多少个;如果不存在,说明理由.
解:以AB的中点为原点,AB所在直线为x轴,建立如图所示平面直角坐标系.
设P(t,1)是线段CD上一点,则-2≤t≤2,
因为AP⊥BP的充要条件是⊥,即·=0,即
解得t=或t=-,所以满足条件的P点存在,而且有两个.
(-2-t)(2-t)+1=0.
A(-2,0),B(2,0),C(2,1),D(-2,1).
由题可得
=(-2-t,-1),=(2-t,-1).
而且
练一练
已知△ABC是直角三角形,斜边BC的中点为M,证明:|AM|=|BC|.
证明:如图所示,以Rt△ABC的直角边AB,AC所在直线为坐标轴,
建立平面直角坐标系.设B,C两点的坐标分别为(b,0),(0,c).
因为点M是BC的中点,所以点M的坐标为
所以
C
A
B
M
根据本节课所学回答下列问题:
(1)平面直角坐标系中两点间距离和中点坐标如何求?
(2)用坐标法解决问题时,建立坐标系应遵循哪些原则?
