2.2.4 点到直线的距离 课件(共22张PPT)
文档属性
| 名称 | 2.2.4 点到直线的距离 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 601.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-12 07:54:44 | ||
图片预览





文档简介
(共22张PPT)
2.2.4 点到直线的距离
新授课
情境:
如图,在铁路的附近有一大型仓库,现要修建一公路与之连接起来,那么怎样设计能使公路最短?
1.掌握点到直线、两条平行直线之间的距离公式,能应用两个距离公式解决有关距离问题
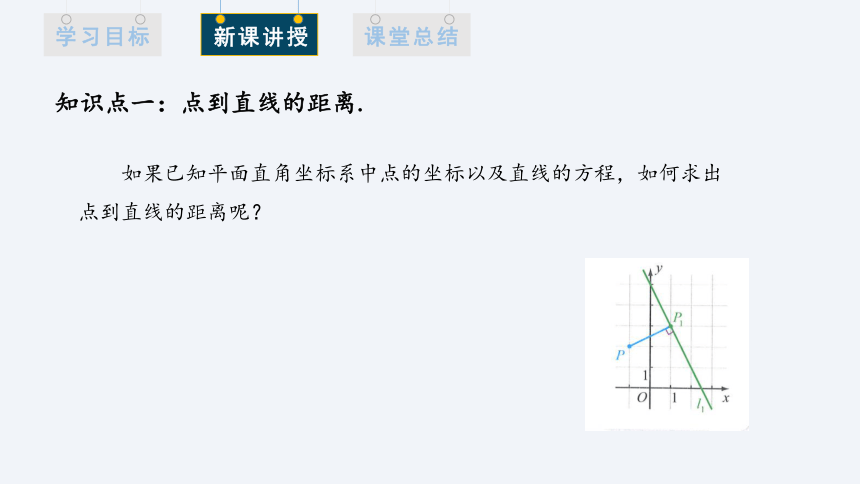
知识点一:点到直线的距离.
如果已知平面直角坐标系中点的坐标以及直线的方程,如何求出点到直线的距离呢?
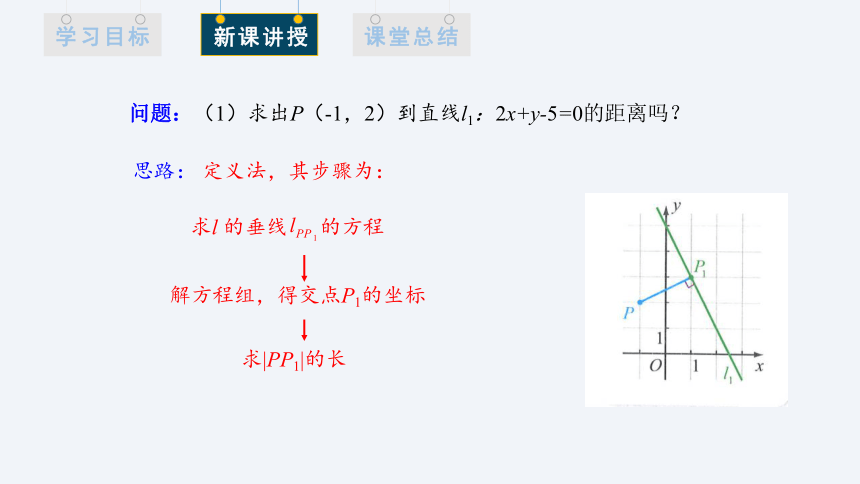
问题:(1)求出P(-1,2)到直线l1:2x+y-5=0的距离吗?
思路: 定义法,其步骤为:
求l 的垂线 的方程
解方程组,得交点P1的坐标
求|PP1|的长
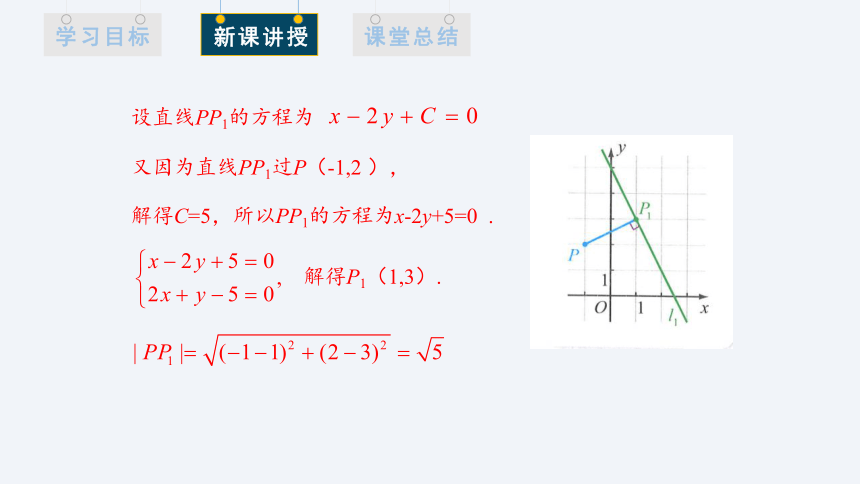
设直线PP1的方程为
又因为直线PP1过P(-1,2 ),
解得C=5,所以PP1的方程为x-2y+5=0 .
解得P1(1,3).
(2)求 到直线 的距离d .
设直线PP1的方程为
又因为直线PP1过 ,
直线PP1方程为
所以
①
②
解得
联立方程
方法一:
点到直线的距离公式
因此
代入l1,PP1直线方程得:
设
则
①
②
方法二:
③
②化简得:
④
①两边同时减去Ax0,By0,整理得
③
④
⑦
将④与⑥两边平方后相加可得:
因此
从而
x
y
O
l
P1
思考:(1)如图,直线PP1垂直于直线l,P2为直线上一点, 为l的法向量,则向量 可以怎样表示?
设 是直线 l 上任意一点,
则 到直线 l 的距离d 满足
是直线 l 的一个法向量
(2)从向量角度考虑,求 到直线 的距离.
x
y
O
l
P1
又因为 是直线 l 上的点,所以
从而
即
因为
1.点(1,-1)到直线 x-y+1=0的距离是( )
C
练一练
例1 已知△ABC的三个顶点A(2,2),B(2,0),C(0,1),
求△ABC的BC边上的高.
整理为一般式方程为
因此所求高为
A(2,2)
2
C
x
y
O
B
1
解:直线BC的方程为
知识点二:两条平行直线之间的距离
思考:根据点到直线距离的求法,如何求两条平行线之间的距离?
两条平行线之间的距离,等于其中一条直线上任意一点到另一条直线的距离.因此,可以借助点到直线的距离求两条平行直线之间的距离.
d
例2 求平行线 与
之间的距离.
解:在l1的方程中,令y=0,则x=-1,因此(-1,0)为直线l1上一点.
又因为(-1,0)到6x-8y-5=0的距离为
所以所求距离为
例3 已知直线
求证:两条直线的距离为
解:设P(x1,y1)为l1上一点,则:
从而
因为P到l2的距离为
所以结论成立
思考:观察直线 Ax + By + C1 = 0与Ax + By + C2 = 0 的形式,说说上述式子有什么需要注意的?
归纳小结
两平行直线间距离公式:已知两条直线 Ax + By + C1 = 0 与 Ax + By + C2 = 0 平行,则它们的距离为:
注意:① 直线方程要化成一般式; ② 两直线方程中 x,y 的系数要相同.
练一练
已知两平行直线l1:3x+5y+1=0和l2:6x+10y+5=0,求l1与l2间的距离.
解:l2:6x+10y+5=0可以化为3x+5y+=0,
∴l1与l2间的距离
根据今天所学回答下列问题:
1.点到直线的距离公式是什么?
2.两条平行直线之间的距离公式如何表示?
2.2.4 点到直线的距离
新授课
情境:
如图,在铁路的附近有一大型仓库,现要修建一公路与之连接起来,那么怎样设计能使公路最短?
1.掌握点到直线、两条平行直线之间的距离公式,能应用两个距离公式解决有关距离问题
知识点一:点到直线的距离.
如果已知平面直角坐标系中点的坐标以及直线的方程,如何求出点到直线的距离呢?
问题:(1)求出P(-1,2)到直线l1:2x+y-5=0的距离吗?
思路: 定义法,其步骤为:
求l 的垂线 的方程
解方程组,得交点P1的坐标
求|PP1|的长
设直线PP1的方程为
又因为直线PP1过P(-1,2 ),
解得C=5,所以PP1的方程为x-2y+5=0 .
解得P1(1,3).
(2)求 到直线 的距离d .
设直线PP1的方程为
又因为直线PP1过 ,
直线PP1方程为
所以
①
②
解得
联立方程
方法一:
点到直线的距离公式
因此
代入l1,PP1直线方程得:
设
则
①
②
方法二:
③
②化简得:
④
①两边同时减去Ax0,By0,整理得
③
④
⑦
将④与⑥两边平方后相加可得:
因此
从而
x
y
O
l
P1
思考:(1)如图,直线PP1垂直于直线l,P2为直线上一点, 为l的法向量,则向量 可以怎样表示?
设 是直线 l 上任意一点,
则 到直线 l 的距离d 满足
是直线 l 的一个法向量
(2)从向量角度考虑,求 到直线 的距离.
x
y
O
l
P1
又因为 是直线 l 上的点,所以
从而
即
因为
1.点(1,-1)到直线 x-y+1=0的距离是( )
C
练一练
例1 已知△ABC的三个顶点A(2,2),B(2,0),C(0,1),
求△ABC的BC边上的高.
整理为一般式方程为
因此所求高为
A(2,2)
2
C
x
y
O
B
1
解:直线BC的方程为
知识点二:两条平行直线之间的距离
思考:根据点到直线距离的求法,如何求两条平行线之间的距离?
两条平行线之间的距离,等于其中一条直线上任意一点到另一条直线的距离.因此,可以借助点到直线的距离求两条平行直线之间的距离.
d
例2 求平行线 与
之间的距离.
解:在l1的方程中,令y=0,则x=-1,因此(-1,0)为直线l1上一点.
又因为(-1,0)到6x-8y-5=0的距离为
所以所求距离为
例3 已知直线
求证:两条直线的距离为
解:设P(x1,y1)为l1上一点,则:
从而
因为P到l2的距离为
所以结论成立
思考:观察直线 Ax + By + C1 = 0与Ax + By + C2 = 0 的形式,说说上述式子有什么需要注意的?
归纳小结
两平行直线间距离公式:已知两条直线 Ax + By + C1 = 0 与 Ax + By + C2 = 0 平行,则它们的距离为:
注意:① 直线方程要化成一般式; ② 两直线方程中 x,y 的系数要相同.
练一练
已知两平行直线l1:3x+5y+1=0和l2:6x+10y+5=0,求l1与l2间的距离.
解:l2:6x+10y+5=0可以化为3x+5y+=0,
∴l1与l2间的距离
根据今天所学回答下列问题:
1.点到直线的距离公式是什么?
2.两条平行直线之间的距离公式如何表示?
