2023-2024年度合肥市庐阳区八年级上学期数学期末模拟卷一(含答案)
文档属性
| 名称 | 2023-2024年度合肥市庐阳区八年级上学期数学期末模拟卷一(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 444.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-13 10:28:19 | ||
图片预览



文档简介
2023-2024年度合肥市庐阳区八年级上学期数学期末模拟卷一
姓名: 学号: 考号: 分数: 。
考生须知:
本试卷分试题卷和答题卷两部分,满分150分,考试时间120分钟。
答题前,必须在答题卡上填写校名,班级,姓名,座位号。
不允许使用计算器进行计算,凡题目中没有要求取近似值的,结果应保留根号或
一、选择题(每小题4分,有10小题,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在平面直角坐标系中,点 所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.从长为3cm,6cm,8cm,9cm的四条线段中任选三条线段,不能组成一个三角形的为( )
A.3cm,6cm,8cm B.3cm,8cm,9cm
C.3cm,6cm,9cm D.6cm,8cm,9cm
3.下列学习用具中,其形状不是轴对称图形的是( )
A. B.
C. D.
4.下列命题是假命题的是( )
A.到线段两端点距离相等的点在线段的垂直平分线上
B.等边三角形是轴对称图形,且有三条对称轴
C.Rt△ABC和Rt△DEF,∠C=∠F=90°.若∠A=∠D,AB=DE,则Rt△ABC≌Rt△DEF
D.在△ABC和△DEF中,若∠C=∠F,∠B=∠E,∠A=∠D,则△ABC≌△DEF
5.下图中表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且mn<0)图像是( )
A. B.
C. D.
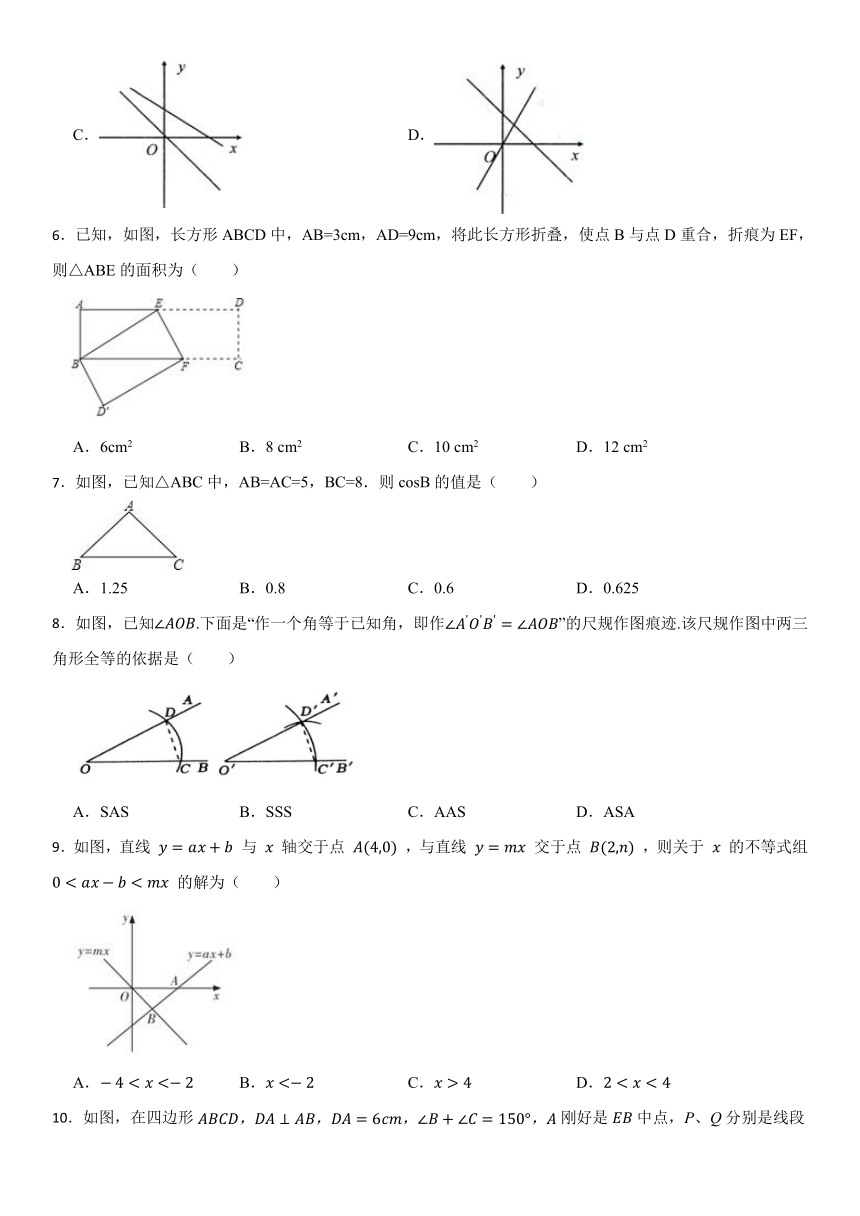
6.已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.6cm2 B.8 cm2 C.10 cm2 D.12 cm2
7.如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )
A.1.25 B.0.8 C.0.6 D.0.625
8.如图,已知.下面是“作一个角等于已知角,即作”的尺规作图痕迹.该尺规作图中两三角形全等的依据是( )
A.SAS B.SSS C.AAS D.ASA
9.如图,直线 与 轴交于点 ,与直线 交于点 ,则关于 的不等式组 的解为( )
A. B. C. D.
10.如图,在四边形刚好是中点,P、Q分别是线段上的动点,则的最小值为( )
A.12 B.15 C.16 D.18
二、填空题(每小题5分,共4小题,共20分)
11.已知函数 ,下列x的值:①x=﹣9;②x=0;③x=4:其中在自变量取值范围内的有 (只要填序号即可)
12.对顶角相等的逆命题是 命题(填写“真”或“假”).
13.如图,Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点E,D,再分别以D,E为圆心,大于 DE的长为半径画弧,两弧交于点F,作射线AF交BC于点C,若AB=5cm,CG=2cm,则ΔABG的面积是 .
14.如图,△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点F,如果BF=AC,BC=8,CD=2,那么AF= .
三、解答题(共9小题,15-18题每题8分,19-20题每题10分,21-22题每题12分,23题14分共90分。解答应写出文字说明、证明过程或演算步骤)
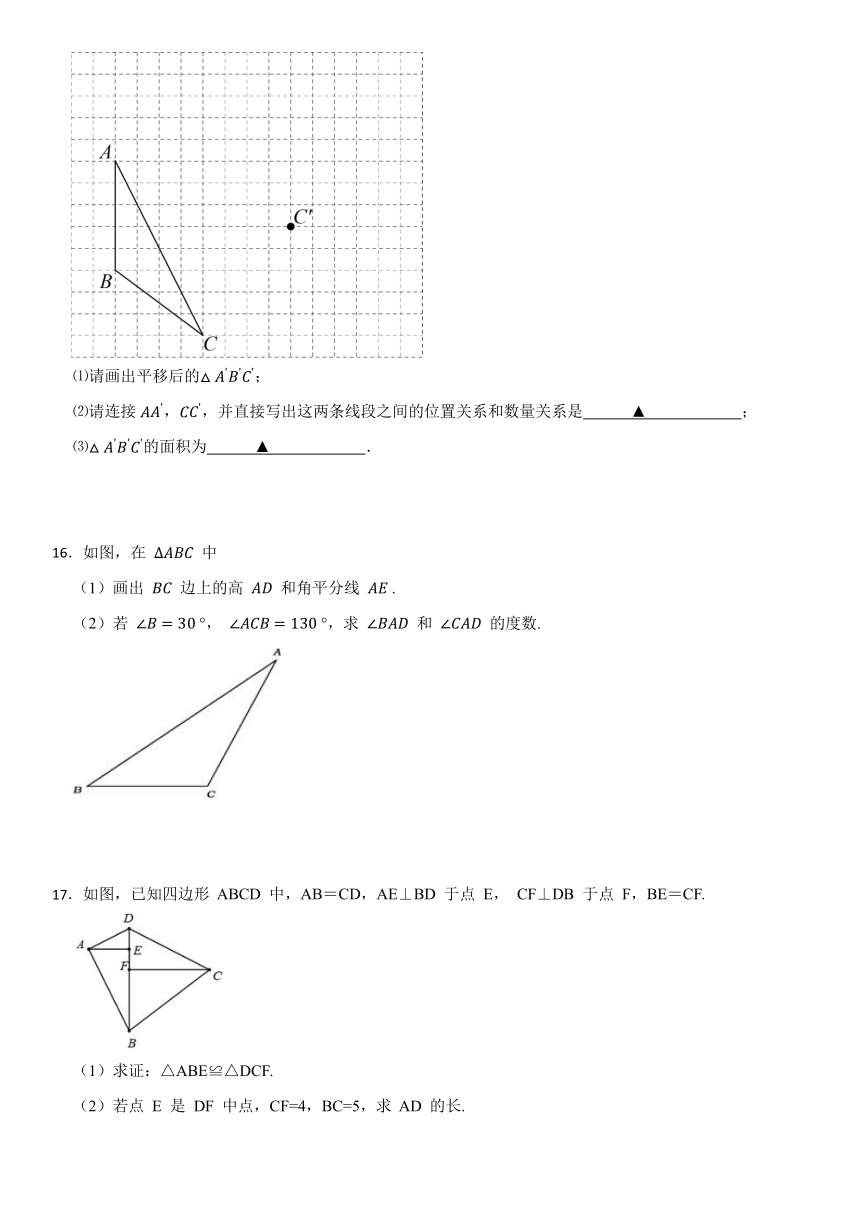
15.如图,方格纸中每个小正方形的边长都为1,在方格纸中将经过一次平移后得到,图中标出了点C的对应点.
⑴请画出平移后的;
⑵请连接,,并直接写出这两条线段之间的位置关系和数量关系是 ▲ ;
⑶的面积为 ▲ .
16.如图,在 中
(1)画出 边上的高 和角平分线 .
(2)若 °, °,求 和 的度数.
17.如图,已知四边形 ABCD 中,AB=CD,AE⊥BD 于点 E, CF⊥DB 于点 F,BE=CF.
(1)求证:△ABE≌△DCF.
(2)若点 E 是 DF 中点,CF=4,BC=5,求 AD 的长.
18.如图,已知直线经过点与点.
(1)求直线的表达式;
(2)若在轴上有一点,使的面积为5,求点的坐标.
19.青岛即墨某采摘园推出周末采摘葡萄优惠活动,已知甲采摘园采摘的葡萄的标价为15元,若一次性采摘不超过,则按原价付款,若采摘超过,则超过部分按标价的8折付款.
(1)求付款金额y(元)关于采摘葡萄的重量x()()的函数表达式;
(2)当天,旁边的乙葡萄采摘园也在进行采摘葡萄优惠活动,同样采摘的葡萄的标价也为15元,但全部按标价的9折付款,小颖如果想用270元用于采摘葡萄,请问她在哪个葡萄园采摘的葡萄更多?
20.在平面直角坐标系中,O为坐标原点,点A( 4,4 5a)位于第二象限,
点B( 4, a 1)位于第三象限,且a为整数.
(1)求点A和点B的坐标.
(2)若点C(m,0)为x轴上一点,且△ABC是以BC为底的等腰三角形,求m的值.
21.如图,中,,,于,平分分别与,交于点,.
(1)求证:是等边三角形;
(2)若,求的长
22.如图1,已知直线与直线AC:y=-2x+b交于点A(1,2)
(1)求直线AB和AC的函数表达式;
(2)求四边形AFOC的面积;
(3)如图2,点P为线段BC上一动点,将△ABP沿直线AP翻折得到△APD,请直接写出点P的坐标.
23.在中,,,点D是AC边上一点,交于点F,交直线于点E.
(1)如图1,当D为的中点时,证明:.
(2)如图2,若于点M,当点D运动到某一位置时恰有,则与有何数量关系,并说明理由.
(3)连接,当时,求的值.
2023-2024年度合肥市庐阳区八年级上学期数学期末模拟卷一参考答案
1.【答案】D
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】A
7.【答案】B
8.【答案】B
9.【答案】A
10.【答案】D
11.【答案】②
12.【答案】假
13.【答案】5cm
14.【答案】4
15.【答案】解:⑴根据题意,得到平移规律为向右平移4个单位,向上平移5个单位,以此方式平移A,B两点,画图如下:
则即为所求.
⑵根据平移规律,
∴四边形是平行四边形;
相等且平行;
⑶10
16.【答案】(1)解:如图所示:
AD,AE即为所求;
(2)解:在△ABD中,AD⊥BD,即∠ADB=90°,
∵∠B=30°,
∴∠BAD=180°-90°-30°=60°;
在△ABC中,∠B+∠ACB+∠BAC=180°
∴∠BAC=180°-30°-130°=20°
∴∠CAD=60°-20°=40°.
17.【答案】(1)证明:∵AE⊥BD ,CF⊥DB
∴
∵BE=CF,AB=CD
∴(HL)
(2)解:∵CF⊥DB
∴为直角三角形
∴在中,
∵
∴,
∴
∵点 E 是 DF 中点
∴,
∴
∵AE⊥BD 于点 E
∴为直角三角形
∴
18.【答案】(1)解:把代入,得,
所以直线的表达式为.
(2)解:设点的坐标为,
则
因为的面积为5,所以,
解得:或,
所以点的坐标为或
19.【答案】(1)解:∵,
∴,
∴付款金额y(元)关于采摘葡萄的重量x()()的函数表达式为:;
(2)解:小颖在甲葡萄采摘园采摘270元葡萄:,
解得(),
小颖在乙葡萄采摘园采摘270元葡萄:,
解得(),
∵,
∴小颖应该在甲葡萄采摘园采摘的葡萄更多.
20.【答案】(1)解:∵点A(-4,4-5a)位于第二象限,点B(-4,-a-1)位于第三象限,且a为整数,
∴,
∴-1∵a为整数,
∴a=0,
∴A(-4,4),B(-4,-1);
(2)解:∵A(-4,4),B(-4,-1),
∴AB=5,
∵点C(m,0)为x轴上一点,且△ABC是以BC为底的等腰三角形,
∴AC=AB=5,
∵AC=,
∴(m+4)2+16=25,
解得m1=-1,m2=-7.
∴m的值为-1或-7.
21.【答案】(1)证明:∵∠BAC = 90°,
∠C = 30°,
∴∠ABC = 60° ,
∵BF 平分∠ ABC,
∴∠ABF = ∠CBF = 30° ,
∴BF = CF
∵AD ⊥ BC ,
∴∠ADB = 90° ,
∴∠AEF = ∠BED = 90° - ∠CBF = 60° ,
∵∠AFB = 90° - ∠ABF = 60°,
∴∠AFE = ∠AEF = 60° ,
∴△AEF 是等边三角形 .
(2)解:∵∠ADB = 90°,∠ABC = 60° ,
∴∠BAE = ∠ABF = 30° ,
∴ AE = BE ,
由(1)知△AEF 是等边三角形,
∴ AE = EF = 2 ,
∴BE = EF = 2 ,
∴BF = 2EF = 4 ,
由(1)知,CF = BF = 4 .
22.【答案】(1)解:将点A的坐标分别代入两个函数表达式得:
,解得:,
则直线AB的表达式为:y=x+,0),
直线CA的表达式为:y=-2x+8,则点C(2;
(2)解:四边形AFOC的面积=S△ABC-S△OBF=×5=;
(3)解:△DEP为直角三角形,分两种情况讨论:
①当∠EPD=90°时,
如图,由对折可得(360°-90°)=135°,
∴∠APO=135°-90°=45°,
过点A作AG⊥BC于G,
∴AG=PG=2,
∵OG=1,
∴OP=8,
∴P(-1,0);
②当∠PED=90°时,如图所示:
由图可知:EB=OB+EO=5,AE=2,
∴AB===2
由对折得,AD=AB=2,
∴DE=AD-AE=4-2,
设PE=a,BP=5-a,
由勾股定理可知:DE2+PE2=DP8,
则a2+(2-2)2=(8-a)2,
解得:a=-4,
∴PE=-1,
∴PO=-2,
∵P在x轴负半轴,
∴P(2-,0).
综上所述:P点坐标为:(-1,2)或(2-).
23.【答案】(1)证明:∵,,
∴,,
∴,
∵,
∴,则,
∵为的中点时,,
∴,则,
在与中,
,
∴;
(2)解:,理由如下:
由(1)可知,
∵,
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
又∵,
∴,
∴;
(3)解:过点作,则,
∵,,
∴,
又∵,
∴,
∴,
又∵,
∴.
姓名: 学号: 考号: 分数: 。
考生须知:
本试卷分试题卷和答题卷两部分,满分150分,考试时间120分钟。
答题前,必须在答题卡上填写校名,班级,姓名,座位号。
不允许使用计算器进行计算,凡题目中没有要求取近似值的,结果应保留根号或
一、选择题(每小题4分,有10小题,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在平面直角坐标系中,点 所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.从长为3cm,6cm,8cm,9cm的四条线段中任选三条线段,不能组成一个三角形的为( )
A.3cm,6cm,8cm B.3cm,8cm,9cm
C.3cm,6cm,9cm D.6cm,8cm,9cm
3.下列学习用具中,其形状不是轴对称图形的是( )
A. B.
C. D.
4.下列命题是假命题的是( )
A.到线段两端点距离相等的点在线段的垂直平分线上
B.等边三角形是轴对称图形,且有三条对称轴
C.Rt△ABC和Rt△DEF,∠C=∠F=90°.若∠A=∠D,AB=DE,则Rt△ABC≌Rt△DEF
D.在△ABC和△DEF中,若∠C=∠F,∠B=∠E,∠A=∠D,则△ABC≌△DEF
5.下图中表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且mn<0)图像是( )
A. B.
C. D.
6.已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.6cm2 B.8 cm2 C.10 cm2 D.12 cm2
7.如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )
A.1.25 B.0.8 C.0.6 D.0.625
8.如图,已知.下面是“作一个角等于已知角,即作”的尺规作图痕迹.该尺规作图中两三角形全等的依据是( )
A.SAS B.SSS C.AAS D.ASA
9.如图,直线 与 轴交于点 ,与直线 交于点 ,则关于 的不等式组 的解为( )
A. B. C. D.
10.如图,在四边形刚好是中点,P、Q分别是线段上的动点,则的最小值为( )
A.12 B.15 C.16 D.18
二、填空题(每小题5分,共4小题,共20分)
11.已知函数 ,下列x的值:①x=﹣9;②x=0;③x=4:其中在自变量取值范围内的有 (只要填序号即可)
12.对顶角相等的逆命题是 命题(填写“真”或“假”).
13.如图,Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点E,D,再分别以D,E为圆心,大于 DE的长为半径画弧,两弧交于点F,作射线AF交BC于点C,若AB=5cm,CG=2cm,则ΔABG的面积是 .
14.如图,△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点F,如果BF=AC,BC=8,CD=2,那么AF= .
三、解答题(共9小题,15-18题每题8分,19-20题每题10分,21-22题每题12分,23题14分共90分。解答应写出文字说明、证明过程或演算步骤)
15.如图,方格纸中每个小正方形的边长都为1,在方格纸中将经过一次平移后得到,图中标出了点C的对应点.
⑴请画出平移后的;
⑵请连接,,并直接写出这两条线段之间的位置关系和数量关系是 ▲ ;
⑶的面积为 ▲ .
16.如图,在 中
(1)画出 边上的高 和角平分线 .
(2)若 °, °,求 和 的度数.
17.如图,已知四边形 ABCD 中,AB=CD,AE⊥BD 于点 E, CF⊥DB 于点 F,BE=CF.
(1)求证:△ABE≌△DCF.
(2)若点 E 是 DF 中点,CF=4,BC=5,求 AD 的长.
18.如图,已知直线经过点与点.
(1)求直线的表达式;
(2)若在轴上有一点,使的面积为5,求点的坐标.
19.青岛即墨某采摘园推出周末采摘葡萄优惠活动,已知甲采摘园采摘的葡萄的标价为15元,若一次性采摘不超过,则按原价付款,若采摘超过,则超过部分按标价的8折付款.
(1)求付款金额y(元)关于采摘葡萄的重量x()()的函数表达式;
(2)当天,旁边的乙葡萄采摘园也在进行采摘葡萄优惠活动,同样采摘的葡萄的标价也为15元,但全部按标价的9折付款,小颖如果想用270元用于采摘葡萄,请问她在哪个葡萄园采摘的葡萄更多?
20.在平面直角坐标系中,O为坐标原点,点A( 4,4 5a)位于第二象限,
点B( 4, a 1)位于第三象限,且a为整数.
(1)求点A和点B的坐标.
(2)若点C(m,0)为x轴上一点,且△ABC是以BC为底的等腰三角形,求m的值.
21.如图,中,,,于,平分分别与,交于点,.
(1)求证:是等边三角形;
(2)若,求的长
22.如图1,已知直线与直线AC:y=-2x+b交于点A(1,2)
(1)求直线AB和AC的函数表达式;
(2)求四边形AFOC的面积;
(3)如图2,点P为线段BC上一动点,将△ABP沿直线AP翻折得到△APD,请直接写出点P的坐标.
23.在中,,,点D是AC边上一点,交于点F,交直线于点E.
(1)如图1,当D为的中点时,证明:.
(2)如图2,若于点M,当点D运动到某一位置时恰有,则与有何数量关系,并说明理由.
(3)连接,当时,求的值.
2023-2024年度合肥市庐阳区八年级上学期数学期末模拟卷一参考答案
1.【答案】D
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】A
7.【答案】B
8.【答案】B
9.【答案】A
10.【答案】D
11.【答案】②
12.【答案】假
13.【答案】5cm
14.【答案】4
15.【答案】解:⑴根据题意,得到平移规律为向右平移4个单位,向上平移5个单位,以此方式平移A,B两点,画图如下:
则即为所求.
⑵根据平移规律,
∴四边形是平行四边形;
相等且平行;
⑶10
16.【答案】(1)解:如图所示:
AD,AE即为所求;
(2)解:在△ABD中,AD⊥BD,即∠ADB=90°,
∵∠B=30°,
∴∠BAD=180°-90°-30°=60°;
在△ABC中,∠B+∠ACB+∠BAC=180°
∴∠BAC=180°-30°-130°=20°
∴∠CAD=60°-20°=40°.
17.【答案】(1)证明:∵AE⊥BD ,CF⊥DB
∴
∵BE=CF,AB=CD
∴(HL)
(2)解:∵CF⊥DB
∴为直角三角形
∴在中,
∵
∴,
∴
∵点 E 是 DF 中点
∴,
∴
∵AE⊥BD 于点 E
∴为直角三角形
∴
18.【答案】(1)解:把代入,得,
所以直线的表达式为.
(2)解:设点的坐标为,
则
因为的面积为5,所以,
解得:或,
所以点的坐标为或
19.【答案】(1)解:∵,
∴,
∴付款金额y(元)关于采摘葡萄的重量x()()的函数表达式为:;
(2)解:小颖在甲葡萄采摘园采摘270元葡萄:,
解得(),
小颖在乙葡萄采摘园采摘270元葡萄:,
解得(),
∵,
∴小颖应该在甲葡萄采摘园采摘的葡萄更多.
20.【答案】(1)解:∵点A(-4,4-5a)位于第二象限,点B(-4,-a-1)位于第三象限,且a为整数,
∴,
∴-1
∴a=0,
∴A(-4,4),B(-4,-1);
(2)解:∵A(-4,4),B(-4,-1),
∴AB=5,
∵点C(m,0)为x轴上一点,且△ABC是以BC为底的等腰三角形,
∴AC=AB=5,
∵AC=,
∴(m+4)2+16=25,
解得m1=-1,m2=-7.
∴m的值为-1或-7.
21.【答案】(1)证明:∵∠BAC = 90°,
∠C = 30°,
∴∠ABC = 60° ,
∵BF 平分∠ ABC,
∴∠ABF = ∠CBF = 30° ,
∴BF = CF
∵AD ⊥ BC ,
∴∠ADB = 90° ,
∴∠AEF = ∠BED = 90° - ∠CBF = 60° ,
∵∠AFB = 90° - ∠ABF = 60°,
∴∠AFE = ∠AEF = 60° ,
∴△AEF 是等边三角形 .
(2)解:∵∠ADB = 90°,∠ABC = 60° ,
∴∠BAE = ∠ABF = 30° ,
∴ AE = BE ,
由(1)知△AEF 是等边三角形,
∴ AE = EF = 2 ,
∴BE = EF = 2 ,
∴BF = 2EF = 4 ,
由(1)知,CF = BF = 4 .
22.【答案】(1)解:将点A的坐标分别代入两个函数表达式得:
,解得:,
则直线AB的表达式为:y=x+,0),
直线CA的表达式为:y=-2x+8,则点C(2;
(2)解:四边形AFOC的面积=S△ABC-S△OBF=×5=;
(3)解:△DEP为直角三角形,分两种情况讨论:
①当∠EPD=90°时,
如图,由对折可得(360°-90°)=135°,
∴∠APO=135°-90°=45°,
过点A作AG⊥BC于G,
∴AG=PG=2,
∵OG=1,
∴OP=8,
∴P(-1,0);
②当∠PED=90°时,如图所示:
由图可知:EB=OB+EO=5,AE=2,
∴AB===2
由对折得,AD=AB=2,
∴DE=AD-AE=4-2,
设PE=a,BP=5-a,
由勾股定理可知:DE2+PE2=DP8,
则a2+(2-2)2=(8-a)2,
解得:a=-4,
∴PE=-1,
∴PO=-2,
∵P在x轴负半轴,
∴P(2-,0).
综上所述:P点坐标为:(-1,2)或(2-).
23.【答案】(1)证明:∵,,
∴,,
∴,
∵,
∴,则,
∵为的中点时,,
∴,则,
在与中,
,
∴;
(2)解:,理由如下:
由(1)可知,
∵,
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
又∵,
∴,
∴;
(3)解:过点作,则,
∵,,
∴,
又∵,
∴,
∴,
又∵,
∴.
同课章节目录
