分解因式知识整理1(浙江省台州市)
文档属性
| 名称 | 分解因式知识整理1(浙江省台州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 483.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-24 00:00:00 | ||
图片预览






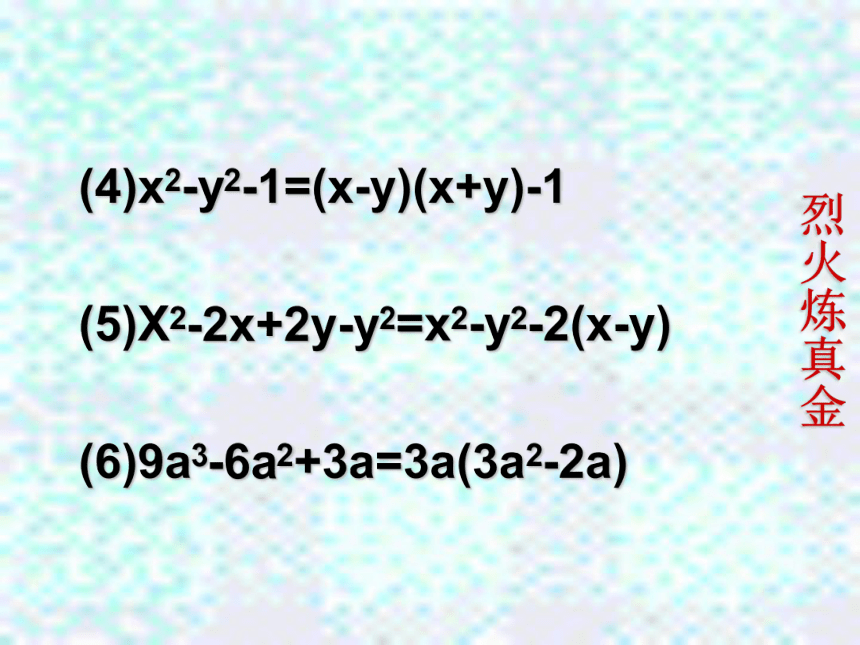


文档简介
课件24张PPT。八年级(上)数学多媒体课件新课程
新思想
新理念因式分解知识整理因式分解重难点1.弄清因式分解与整式乘法的区别因式分解是和差化为积的形式,与整式乘法是互逆的两个过程.因式分解重难点2.因式分解的方法有:
提取公因式法(公因式要提尽,提取负号括号内要变号);
运用公式法(符合公式特点,变形后凑成平方差公式或完全平方公式). 3. 分解因式的步骤是先提取公因式,再运用公式,直到不能再分解为止.知识规律重点问题一:理解因式分解的概念例1.下列从左到右,哪些是 因式分解,哪些不是?
(1)a(a+b-c)=a2+ab-ac
(2)x2-2x+4=x2-2(x-2)
(3)a(x2-9)=a(x-3)(x+3) (4)x2-y2-1=(x-y)(x+y)-1
(5)X2-2x+2y-y2=x2-y2-2(x-y)
(6)9a3-6a2+3a=3a(3a2-2a)
思考与解答分析:(1)是乘法运算.(2)(4)(5)的右边不是乘积形式.(6)的右边漏掉了1这一项,只有(3)把多项式化成了积的形式,且二式不可再分.
解答:(3)是因式分解,其它都不是.思考与解答分析:(1)是乘法运算.(2)(4)(5)的右边不是乘积形式.(6)的右边漏掉了1这一项,只有(3)把多项式化成了积的形式,且二式不可再分.
解答:(3)是因式分解,其它都不是.重点问题二: 提取公因式法例 2 分解因式:
(1)12a2b-18ab2-24a3b3
(2)-9m2n+27mn2-18mn
(3)5a2(x-y)+10a(y-x)
(4)6x(x-y)2+3(y-x)3 思考与解答(1)分析:各项系数的最大公约数是6,相同字母最低次幂是 ab, 最大公因式是6ab,提取后括号内的项数与原项数相同.
解答:
原式=6ab(2a-3b-4a2b2) (2)分析:首项为负,提取负号后,括号内各项要变号.
解答:原式=-9 mn(m-3n+2)
[ =9mn(3n-m-2) ]
(3)分析:把y-x变为 –(x-y)可找到公因式,单项式写在多项式的前面. 解答:原式=5a2(x-y)-10a(x-y)
=5a(x-y)(a-2)(4)分析 :(x-y)2=(y-x)2,且(y-x)3= -(x-y)3 可找到公因式是3(x-y)2
解答:原式=6 (x-y)2-3(x-y)3
=3(x-y)2[2x-(x-y)]
=3(X-y)2(x+y)
1.提取公因式法是因式分解最基本的方法,用这种方法进行因式分解的关键是确定多项式的公因式,同时要注意:
①公因式要提尽;②不要漏掉因式1;③多项式首项取正号;小结2.多项式的公因式:
多项式各项系数的最大公约数与相同字母的最低幂的积就是多项式的公因式.在因式分解中若多项式第一项系数为负数时,所提公因式应带符号,括号内均要变号.
重点三:运用公式法例3. 下列多项式能否用 公式法分解因式?
(1)a2+36 (2)-x2-4y2
(3)9(a+b)2-25c2 (4)m2+6mn+4n2
(5)-4a2-12ab+9b2 分析: 紧扣平方差公式和完全平方公式的结构特点,看题中是否具有.
解答:只有(3)能用公式法分解因式,余都不能.例5 用公式法分解因式:
(1)4a2-4a+1
(2)16(a-b)2-(a+b)2
(3)9(p-q)2-6(q-p)+1
(4)x6+24x3+144例5 用公式法分解因式:
(1)4a2-4a+1
(2)16(a-b)2-(a+b)2
(3)9(p-q)2-6(q-p)+1
(4)x6+24x3+144思考与解答(1)运用完全平方分式得:
4a2-4a+1=(2a)2-2?(2a)?1+12
=(2a-1)2
(2)把(a-b),(a+b)当作一个整体得:
16(a-b)2-(a+b)2=[4(a-b)]2-(a+b)2
= [4(a-b)+ (a+b)][4(a-b)- (a+b)]
=(5a-3b)(3a-5b)思考与解答(1)运用完全平方分式得:
4a2-4a+1=(2a)2-2?(2a)?1+12
=(2a-1)2
(2)把(a-b),(a+b)当作一个整体得:
16(a-b)2-(a+b)2=[4(a-b)]2-(a+b)2
= [4(a-b)+ (a+b)][4(a-b)- (a+b)]
=(5a-3b)(3a-5b)(3)把(p-q)当作一个整体进行分解 9(p-q)2-6(q-p)+1 =[3(p-q)]2+2·3· (p-q)+12 =[3(p-q)+1]2=(3p-3q+1)2 (4)分析:x6=(x3)2,把x3看成一个整体可解. x6+24x3+144
=(x3)2+2? (x3) ? 12+122
=(x3+12)2(3)把(p-q)当作一个整体进行分解 9(p-q)2-6(q-p)+1 =[3(p-q)]2+2·3· (p-q)+12 =[3(p-q)+1]2=(3p-3q+1)2 (4)分析:x6=(x3)2,把x3看成一个整体可解. x6+24x3+144
=(x3)2+2? (x3) ? 12+122
=(x3+12)21.要选择相应的公式进行因式分解,首先要观察它的项数,各项的系数,次数是否符合公式的特点,
其次再观察多项式,若是二项式,应考虑平方差公式,若是三项式,则考虑完全平方公式.小结
公式中的字母,可表示一个数,一个单项式或者一个多项式.2.分解因式的步骤是先提取公因式,再运用公式,直到不能再分解为止.
3.因式分解与它所在的数集有关,当有理数集还没有扩充之前,多项式的因式分解都是在有理数集上进行的.重点问题四:灵活选用方法分解因式
重点问题五: 因式分解的应用下节课内容再会!
新思想
新理念因式分解知识整理因式分解重难点1.弄清因式分解与整式乘法的区别因式分解是和差化为积的形式,与整式乘法是互逆的两个过程.因式分解重难点2.因式分解的方法有:
提取公因式法(公因式要提尽,提取负号括号内要变号);
运用公式法(符合公式特点,变形后凑成平方差公式或完全平方公式). 3. 分解因式的步骤是先提取公因式,再运用公式,直到不能再分解为止.知识规律重点问题一:理解因式分解的概念例1.下列从左到右,哪些是 因式分解,哪些不是?
(1)a(a+b-c)=a2+ab-ac
(2)x2-2x+4=x2-2(x-2)
(3)a(x2-9)=a(x-3)(x+3) (4)x2-y2-1=(x-y)(x+y)-1
(5)X2-2x+2y-y2=x2-y2-2(x-y)
(6)9a3-6a2+3a=3a(3a2-2a)
思考与解答分析:(1)是乘法运算.(2)(4)(5)的右边不是乘积形式.(6)的右边漏掉了1这一项,只有(3)把多项式化成了积的形式,且二式不可再分.
解答:(3)是因式分解,其它都不是.思考与解答分析:(1)是乘法运算.(2)(4)(5)的右边不是乘积形式.(6)的右边漏掉了1这一项,只有(3)把多项式化成了积的形式,且二式不可再分.
解答:(3)是因式分解,其它都不是.重点问题二: 提取公因式法例 2 分解因式:
(1)12a2b-18ab2-24a3b3
(2)-9m2n+27mn2-18mn
(3)5a2(x-y)+10a(y-x)
(4)6x(x-y)2+3(y-x)3 思考与解答(1)分析:各项系数的最大公约数是6,相同字母最低次幂是 ab, 最大公因式是6ab,提取后括号内的项数与原项数相同.
解答:
原式=6ab(2a-3b-4a2b2) (2)分析:首项为负,提取负号后,括号内各项要变号.
解答:原式=-9 mn(m-3n+2)
[ =9mn(3n-m-2) ]
(3)分析:把y-x变为 –(x-y)可找到公因式,单项式写在多项式的前面. 解答:原式=5a2(x-y)-10a(x-y)
=5a(x-y)(a-2)(4)分析 :(x-y)2=(y-x)2,且(y-x)3= -(x-y)3 可找到公因式是3(x-y)2
解答:原式=6 (x-y)2-3(x-y)3
=3(x-y)2[2x-(x-y)]
=3(X-y)2(x+y)
1.提取公因式法是因式分解最基本的方法,用这种方法进行因式分解的关键是确定多项式的公因式,同时要注意:
①公因式要提尽;②不要漏掉因式1;③多项式首项取正号;小结2.多项式的公因式:
多项式各项系数的最大公约数与相同字母的最低幂的积就是多项式的公因式.在因式分解中若多项式第一项系数为负数时,所提公因式应带符号,括号内均要变号.
重点三:运用公式法例3. 下列多项式能否用 公式法分解因式?
(1)a2+36 (2)-x2-4y2
(3)9(a+b)2-25c2 (4)m2+6mn+4n2
(5)-4a2-12ab+9b2 分析: 紧扣平方差公式和完全平方公式的结构特点,看题中是否具有.
解答:只有(3)能用公式法分解因式,余都不能.例5 用公式法分解因式:
(1)4a2-4a+1
(2)16(a-b)2-(a+b)2
(3)9(p-q)2-6(q-p)+1
(4)x6+24x3+144例5 用公式法分解因式:
(1)4a2-4a+1
(2)16(a-b)2-(a+b)2
(3)9(p-q)2-6(q-p)+1
(4)x6+24x3+144思考与解答(1)运用完全平方分式得:
4a2-4a+1=(2a)2-2?(2a)?1+12
=(2a-1)2
(2)把(a-b),(a+b)当作一个整体得:
16(a-b)2-(a+b)2=[4(a-b)]2-(a+b)2
= [4(a-b)+ (a+b)][4(a-b)- (a+b)]
=(5a-3b)(3a-5b)思考与解答(1)运用完全平方分式得:
4a2-4a+1=(2a)2-2?(2a)?1+12
=(2a-1)2
(2)把(a-b),(a+b)当作一个整体得:
16(a-b)2-(a+b)2=[4(a-b)]2-(a+b)2
= [4(a-b)+ (a+b)][4(a-b)- (a+b)]
=(5a-3b)(3a-5b)(3)把(p-q)当作一个整体进行分解 9(p-q)2-6(q-p)+1 =[3(p-q)]2+2·3· (p-q)+12 =[3(p-q)+1]2=(3p-3q+1)2 (4)分析:x6=(x3)2,把x3看成一个整体可解. x6+24x3+144
=(x3)2+2? (x3) ? 12+122
=(x3+12)2(3)把(p-q)当作一个整体进行分解 9(p-q)2-6(q-p)+1 =[3(p-q)]2+2·3· (p-q)+12 =[3(p-q)+1]2=(3p-3q+1)2 (4)分析:x6=(x3)2,把x3看成一个整体可解. x6+24x3+144
=(x3)2+2? (x3) ? 12+122
=(x3+12)21.要选择相应的公式进行因式分解,首先要观察它的项数,各项的系数,次数是否符合公式的特点,
其次再观察多项式,若是二项式,应考虑平方差公式,若是三项式,则考虑完全平方公式.小结
公式中的字母,可表示一个数,一个单项式或者一个多项式.2.分解因式的步骤是先提取公因式,再运用公式,直到不能再分解为止.
3.因式分解与它所在的数集有关,当有理数集还没有扩充之前,多项式的因式分解都是在有理数集上进行的.重点问题四:灵活选用方法分解因式
重点问题五: 因式分解的应用下节课内容再会!
