分解因式知识整理2(浙江省台州市)
文档属性
| 名称 | 分解因式知识整理2(浙江省台州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 854.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-24 14:50:00 | ||
图片预览




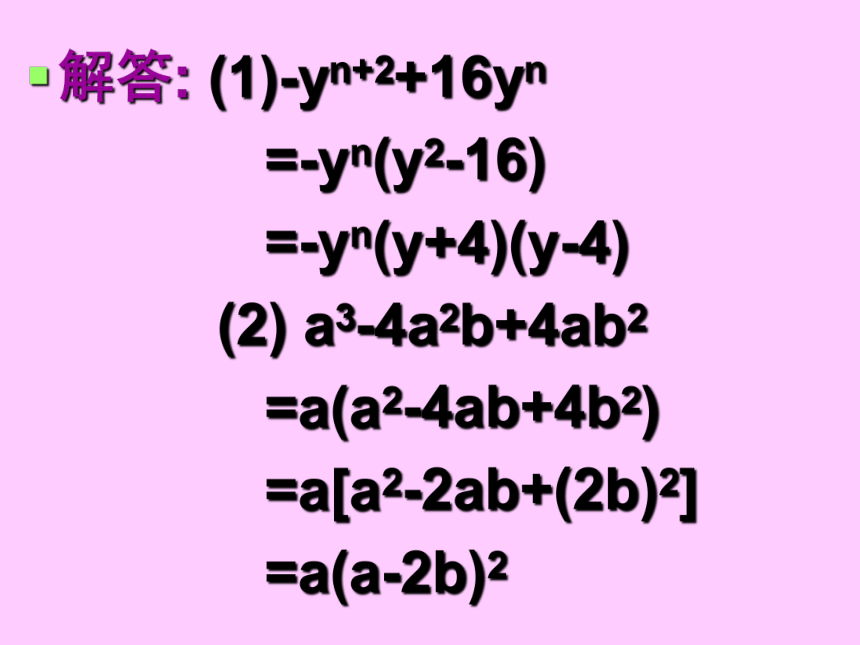
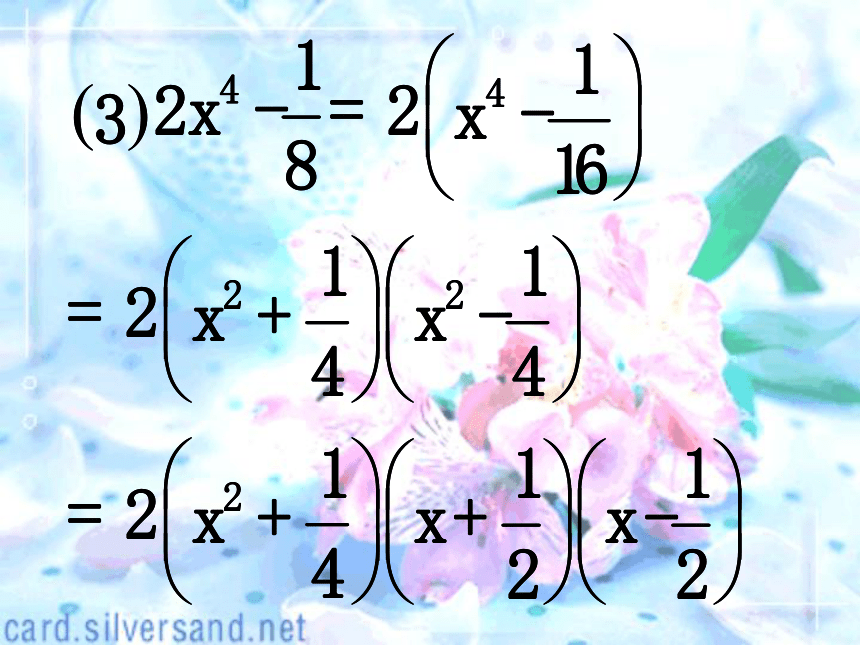

文档简介
课件15张PPT。八年级(上)数学多媒体课件新课程
新思想
新理念因式分解知识整理(二)重点问题四: 灵活选用方法进行因式分解例1.把下列各式分解因式
(1)-yn+2+16yn
(2)a3-4a2b+4ab2
思维方式:有公因式先提取公因式,再运用公式进行分解.直到完全分解为止.有时可采用凑合的办法达到运用公式的目的. 分析与解答解答: (1)-yn+2+16yn
=-yn(y2-16)
=-yn(y+4)(y-4)
(2) a3-4a2b+4ab2
=a(a2-4ab+4b2)
=a[a2-2ab+(2b)2]
=a(a-2b)2采用配凑法使之符合完全平方公式.例题2.分解因式(1) (m-2n)2+6(2n-m)(m+n)
+9(m+n)2
(2)(x2-2x)2+2(x2-2x)+1分析:整体处理思想,即把m-2n, m+n,x2-2x分别当成一个整体, 使之符合公式形式.解(1)原式= (m-2n)2-2?3(m-2n)(m+n)+[3(m+n)]2 = [(m-2n)-3(m+n)] 2 =(-2m-5n)2=(2m+5n)2解(2) (x2-2x)2+2(x2-2x)+1
=(x2-2x)2+2(x2-2x)·1+12
=(x2-2x+1)2
=[(x-1)2]2=(x-1)4重点问题五: 因式分解的应用例3.计算(1)210-29-28
解答(1)210-29-28
=28(22-2-1)=28(4-2-1)=28例4 求值(1)求当x=0.5时
(x+1)2(2x-3)+(x+1)(2x-3)
+2(x+1)(3-2x)的值
(2)不解方程组 2x+y=6
x-3y=1
求7y(x-3y)2-2(3y-x)3之值(1)求当x=0.5时
(x+1)2(2x-3)+(x+1)(2x-3)
+2(x+1)(3-2x)的值
(2)不解方程组 2x+y=6
x-3y=1
求7y(x-3y)2-2(3y-x)3之值解答(1)先化简,再求值.
原式=(x+1)2(2x-3)+(x+1)(2x-3)
-2(x+1)(2x-3)
=(x+1)(2x-3)[(x+1)+1-2]
=x(x+1)(2x-3)
把x的值代入即得值为-1.5.解答(1)先化简,再求值.
原式=(x+1)2(2x-3)+(x+1)(2x-3)
-2(x+1)(2x-3)
=(x+1)(2x-3)[(x+1)+1-2]
=x(x+1)(2x-3)
把x的值代入即得值为-1.5.解(2) (2)7y(x-3y)2-2(3y-x)3
= 7y(x-3y)2+2(x-3y)3
=(x-3y)2[ 7y+2(x-3y)]
=(x-3y)2(2x+y)
把 2x+y=6, x-3y=1代入即得
原式=6.例题5(1)若n为整数则(2n+1)2-(2n-1)2一定能被8整除,试证明。证明:∵ (2n+1)2-(2n-1)2 =[(2n+1)+(2n-1)][(2n+1)+(2n-1)]
=4n?2=8n
且n为整数,∴8n是8的整数倍,一定能被8整除。
新思想
新理念因式分解知识整理(二)重点问题四: 灵活选用方法进行因式分解例1.把下列各式分解因式
(1)-yn+2+16yn
(2)a3-4a2b+4ab2
思维方式:有公因式先提取公因式,再运用公式进行分解.直到完全分解为止.有时可采用凑合的办法达到运用公式的目的. 分析与解答解答: (1)-yn+2+16yn
=-yn(y2-16)
=-yn(y+4)(y-4)
(2) a3-4a2b+4ab2
=a(a2-4ab+4b2)
=a[a2-2ab+(2b)2]
=a(a-2b)2采用配凑法使之符合完全平方公式.例题2.分解因式(1) (m-2n)2+6(2n-m)(m+n)
+9(m+n)2
(2)(x2-2x)2+2(x2-2x)+1分析:整体处理思想,即把m-2n, m+n,x2-2x分别当成一个整体, 使之符合公式形式.解(1)原式= (m-2n)2-2?3(m-2n)(m+n)+[3(m+n)]2 = [(m-2n)-3(m+n)] 2 =(-2m-5n)2=(2m+5n)2解(2) (x2-2x)2+2(x2-2x)+1
=(x2-2x)2+2(x2-2x)·1+12
=(x2-2x+1)2
=[(x-1)2]2=(x-1)4重点问题五: 因式分解的应用例3.计算(1)210-29-28
解答(1)210-29-28
=28(22-2-1)=28(4-2-1)=28例4 求值(1)求当x=0.5时
(x+1)2(2x-3)+(x+1)(2x-3)
+2(x+1)(3-2x)的值
(2)不解方程组 2x+y=6
x-3y=1
求7y(x-3y)2-2(3y-x)3之值(1)求当x=0.5时
(x+1)2(2x-3)+(x+1)(2x-3)
+2(x+1)(3-2x)的值
(2)不解方程组 2x+y=6
x-3y=1
求7y(x-3y)2-2(3y-x)3之值解答(1)先化简,再求值.
原式=(x+1)2(2x-3)+(x+1)(2x-3)
-2(x+1)(2x-3)
=(x+1)(2x-3)[(x+1)+1-2]
=x(x+1)(2x-3)
把x的值代入即得值为-1.5.解答(1)先化简,再求值.
原式=(x+1)2(2x-3)+(x+1)(2x-3)
-2(x+1)(2x-3)
=(x+1)(2x-3)[(x+1)+1-2]
=x(x+1)(2x-3)
把x的值代入即得值为-1.5.解(2) (2)7y(x-3y)2-2(3y-x)3
= 7y(x-3y)2+2(x-3y)3
=(x-3y)2[ 7y+2(x-3y)]
=(x-3y)2(2x+y)
把 2x+y=6, x-3y=1代入即得
原式=6.例题5(1)若n为整数则(2n+1)2-(2n-1)2一定能被8整除,试证明。证明:∵ (2n+1)2-(2n-1)2 =[(2n+1)+(2n-1)][(2n+1)+(2n-1)]
=4n?2=8n
且n为整数,∴8n是8的整数倍,一定能被8整除。
