圆周角与圆心角的关系(二)(广东省深圳市福田区)
文档属性
| 名称 | 圆周角与圆心角的关系(二)(广东省深圳市福田区) |

|
|
| 格式 | rar | ||
| 文件大小 | 530.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-25 00:00:00 | ||
图片预览


文档简介
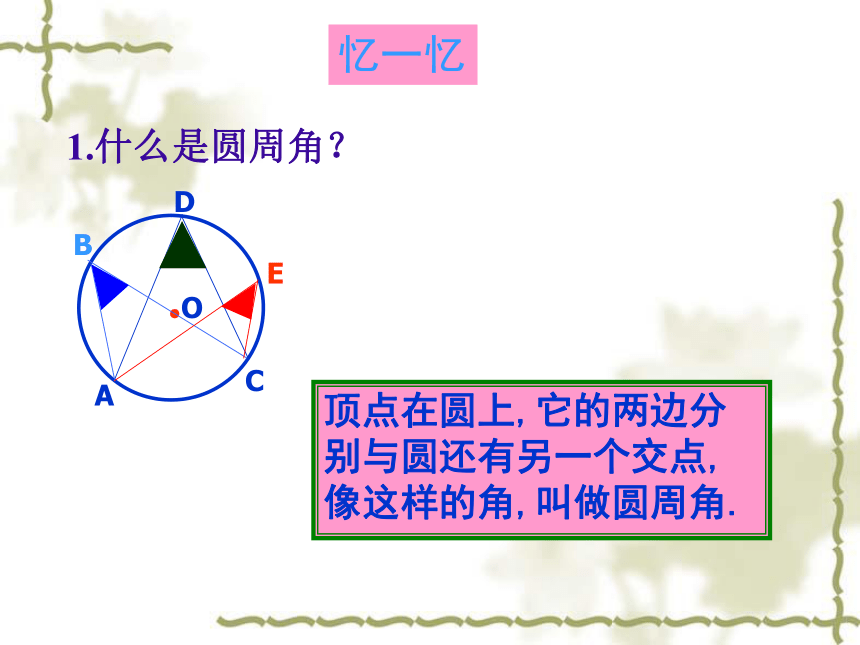
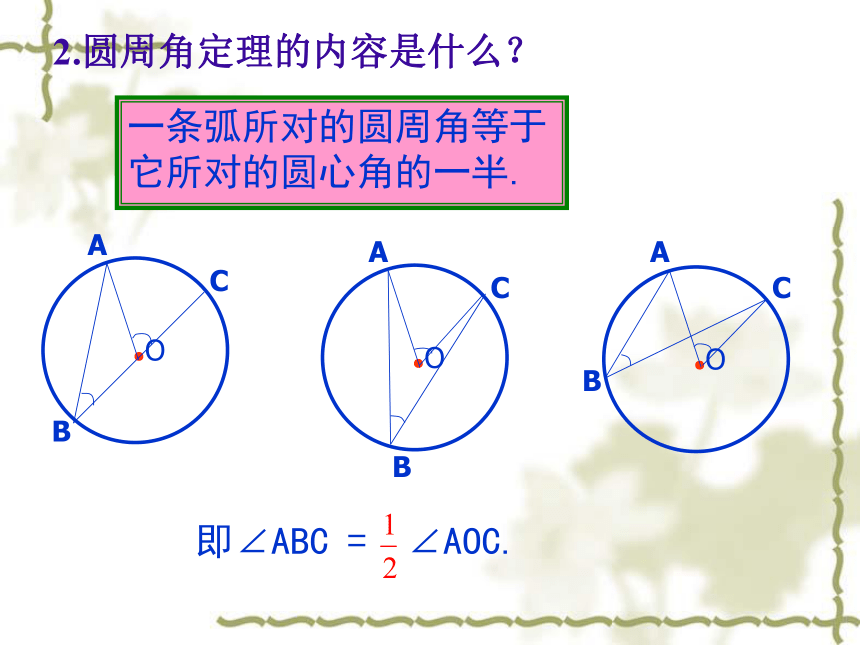
课件27张PPT。圆周角和圆心角的关系(二)1.什么是圆周角?顶点在圆上,它的两边分别与圆还有另一个交点,像这样的角,叫做圆周角.忆一忆2.圆周角定理的内容是什么?一条弧所对的圆周角等于它所对的圆心角的一半.1.100o的弧所对的圆心角等于_______,所对的圆周角等于_______
2、一弦分圆周成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为______________
3、如图,在⊙O中,∠BAC=32o,则∠BOC=______
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______B
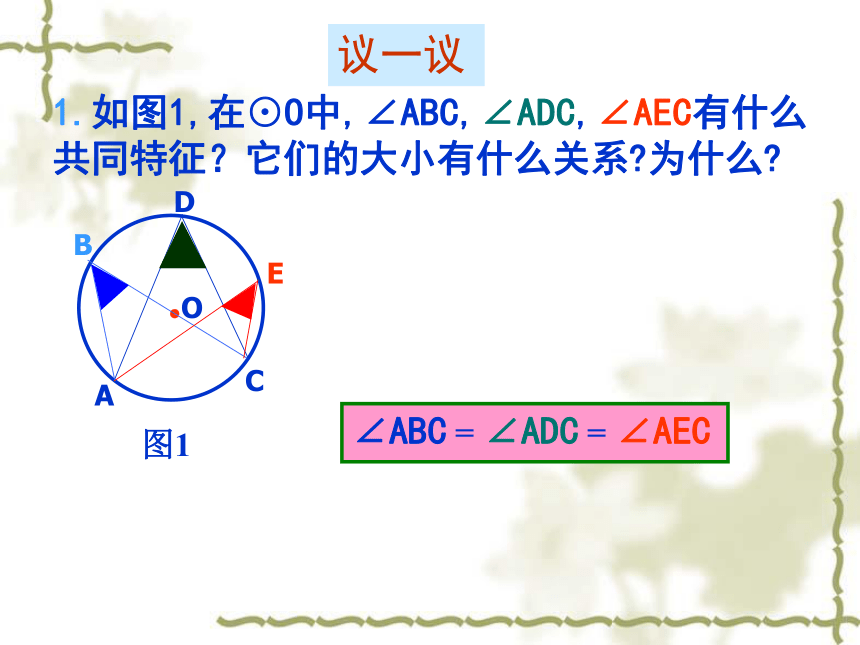
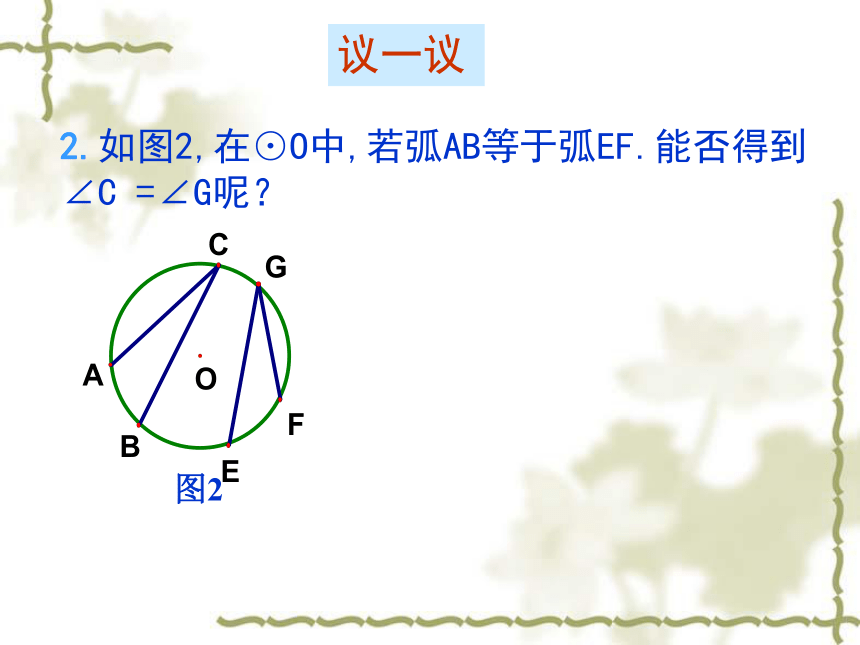
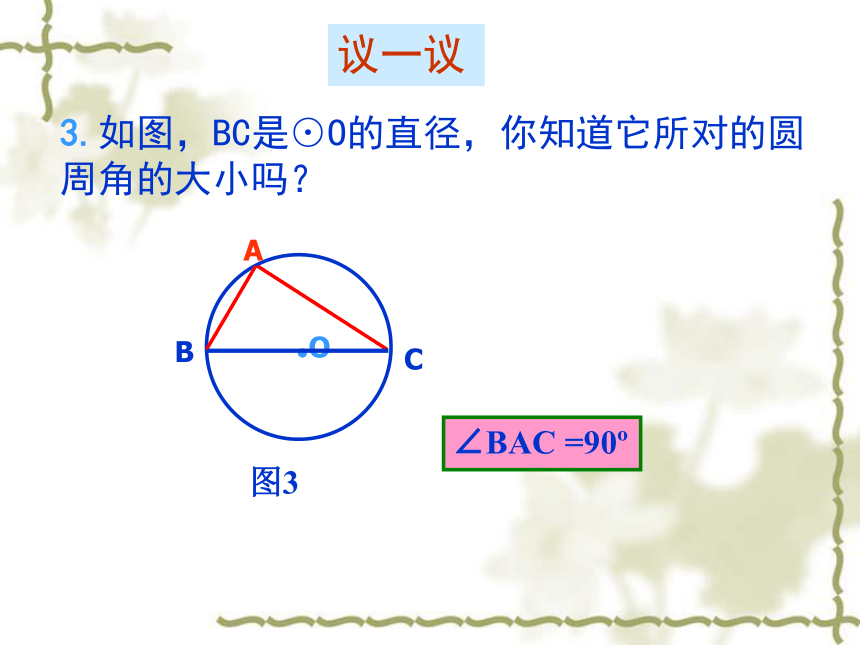
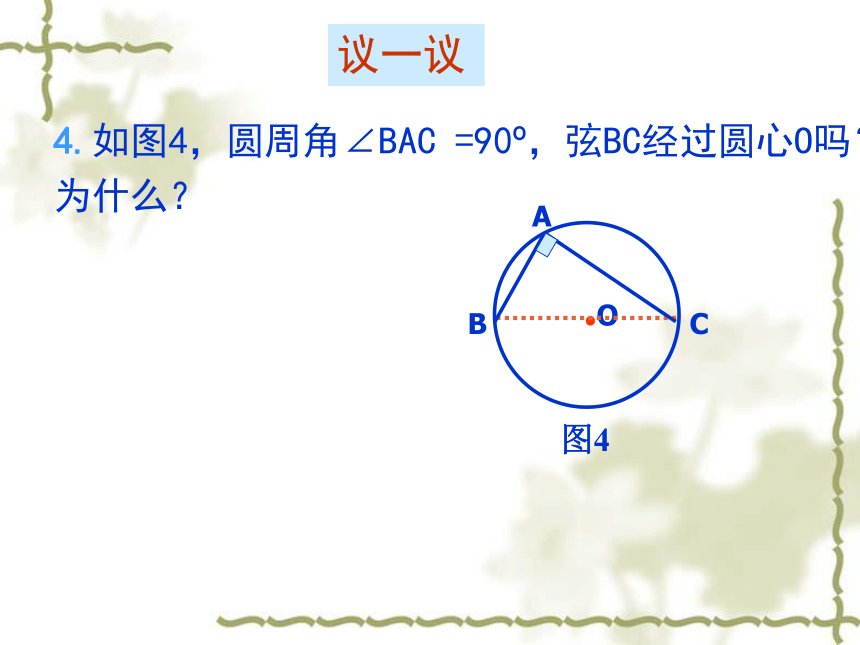
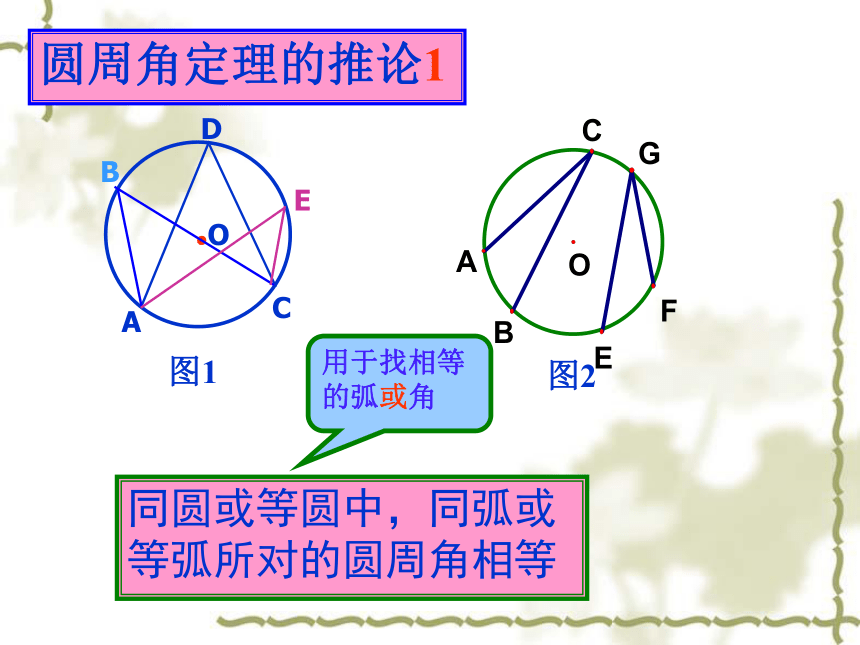
100o50o36o或144o64o100o做一做1.如图1,在⊙O中,∠ABC,∠ADC,∠AEC有什么共同特征?它们的大小有什么关系?为什么?议一议∠ABC = ∠ADC = ∠AEC2.如图2,在⊙O中,若弧AB等于弧EF.能否得到∠C =∠G呢?议一议3.如图,BC是⊙O的直径,你知道它所对的圆周角的大小吗?图3∠BAC =90o议一议4.如图4,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?议一议圆周角定理的推论1同圆或等圆中,同弧或等弧所对的圆周角相等用于找相等的弧或角
圆周角定理的推论2直径所对的圆周角是直角
90°圆周角所对的弦是直径用于判断某条直线是否过圆心
或判断某个圆周角是否是直角6XXX
(1)相等的圆周角所对的弧也相等。( )
(2)90。的角所对的弦是直径。 ( )
(3)同弦所对的圆周角相等。 ( )判断对错
(1)如图所示,
∠BAC= ,∠DAC= .∠DBC∠BDC(2)如图所示,⊙O的直径AB=10cm,
C为⊙O上一点,∠BAC=30°,
则BC= cm 5填一填如图,△ABC的顶点均在⊙O上,
AB=4, ∠C=30°,则⊙O的直径为_____ E8做一做点A、B、C在半径为2cm的⊙O上,若
BC= cm,则∠A的度数为___________。试一试60°或120° 如图,以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则
(1)OC与AD的位置关系是_______;
(2)OC与BD的位置关系是_______;
(3)若OC = 2cm,则BD = ____cm。垂 直平 行4填一填C 1.如图,AB是⊙O的直径,BD是弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?理由是:连接AD
∵AB是⊙O的直径
∴∠ADB=90°
即AD⊥BC
又∵AC=AB
∴BD=CD(三线合一)解: BD=CD试一试实际应用分析 :船所处区域有三种情况:
(1)在⊙O上;(2)在⊙O内;
(3)在⊙O外。
分这三种情况逐一讨论,便可说明。2、船在航行过程中,船长通过测定角度来确定是否会遇到暗礁。如图,A、B表示灯塔,暗礁分布在经过A、B两
点的一个圆形区域内,C表示一个危险临界点, ∠ACB
就是“危险角”。当船与两个灯塔的夹角大于“危险角”时,
就有可能触礁。
(1)当船与两个灯塔的夹角大于“危险角”时,
船位于哪个区域?为什么?
(2)当船与两个灯塔的夹角小于“危险角”时,
船位于哪个区域?为什么? ·oα解: (1)当船与两个灯塔的夹角α大于“危险角”时,船位于暗礁区域内( ⊙O内)。理由如下:
①假设船在⊙O上,则∠ α= ∠C,这与∠ α> ∠C矛盾,所以船不可能在⊙O上;
②假设船在⊙O外,如图,则∠ α< ∠AEB, ∠AEB= ∠C,即∠ α< ∠C,这与∠ α> ∠C矛盾,所以船不可能在⊙O外;
综上所述,船只能在⊙O内。 ·oα解: (2)当船与两个灯塔的夹角α小于“危险角”时,船位于暗礁区域外( ⊙O外)。理由如下:
①假设船在⊙O上,则∠ α= ∠C,这与∠ α< ∠C矛盾,所以船不可能在⊙O上;
②假设船在⊙O内,如图,延长AP交⊙O于E,连接BE,则∠E= ∠C。因为 ∠ α> ∠E, 所以∠ α> ∠C,这与∠ α< ∠C矛盾,所以船不可能在⊙O内;ABCEP·Oα综上所述,船只能在⊙O外。 3、如图,AE⊙O的直径, △ABC的顶点都在⊙O上,AD是△ABC的高; 求证:AB · AC = AE · ADAOBCDE综合运用证明:连结BE
∵AE是⊙O的直径,∴∠ABE=90°
∵ AD是△ABC的高,∴∠ADC=90°
∴∠ADC =∠ABE=900,
∠C =∠E
∴△ADC∽ △ABE
∴∴AB · AC = AE · AD能力拓展4、在直径为AB的半圆内划出一块三角形区域,使三角形的一边为AB,顶点C在半圆周上,其他两边分别为6和8,现要建造一个矩形水池DEFN,使D、E在AB上,N在AC上,F在BC上。设计如图所示的方案,其中使AC=8,BC=6。
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x取何值时,水池DEFN的面积最大?最大值是多少?ADGEBNCFM解:(1)(2)设水池DEFN的面积为y
∵NF∥AB
∴△CNF∽△CAB∴当x=2.4时,水池DEFN的面积最大,最大值是12。1、本节课我们学习了哪些知识?
小结圆周角定理的两个推论引辅助线的方法:
(1)构造直径上的圆周角。
(2)构造同弧所对的圆周角。2、本节课我们学习了哪些方法?同步:P52-53作业谢谢莅临指导!
2、一弦分圆周成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为______________
3、如图,在⊙O中,∠BAC=32o,则∠BOC=______
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______B
100o50o36o或144o64o100o做一做1.如图1,在⊙O中,∠ABC,∠ADC,∠AEC有什么共同特征?它们的大小有什么关系?为什么?议一议∠ABC = ∠ADC = ∠AEC2.如图2,在⊙O中,若弧AB等于弧EF.能否得到∠C =∠G呢?议一议3.如图,BC是⊙O的直径,你知道它所对的圆周角的大小吗?图3∠BAC =90o议一议4.如图4,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?议一议圆周角定理的推论1同圆或等圆中,同弧或等弧所对的圆周角相等用于找相等的弧或角
圆周角定理的推论2直径所对的圆周角是直角
90°圆周角所对的弦是直径用于判断某条直线是否过圆心
或判断某个圆周角是否是直角6XXX
(1)相等的圆周角所对的弧也相等。( )
(2)90。的角所对的弦是直径。 ( )
(3)同弦所对的圆周角相等。 ( )判断对错
(1)如图所示,
∠BAC= ,∠DAC= .∠DBC∠BDC(2)如图所示,⊙O的直径AB=10cm,
C为⊙O上一点,∠BAC=30°,
则BC= cm 5填一填如图,△ABC的顶点均在⊙O上,
AB=4, ∠C=30°,则⊙O的直径为_____ E8做一做点A、B、C在半径为2cm的⊙O上,若
BC= cm,则∠A的度数为___________。试一试60°或120° 如图,以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则
(1)OC与AD的位置关系是_______;
(2)OC与BD的位置关系是_______;
(3)若OC = 2cm,则BD = ____cm。垂 直平 行4填一填C 1.如图,AB是⊙O的直径,BD是弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?理由是:连接AD
∵AB是⊙O的直径
∴∠ADB=90°
即AD⊥BC
又∵AC=AB
∴BD=CD(三线合一)解: BD=CD试一试实际应用分析 :船所处区域有三种情况:
(1)在⊙O上;(2)在⊙O内;
(3)在⊙O外。
分这三种情况逐一讨论,便可说明。2、船在航行过程中,船长通过测定角度来确定是否会遇到暗礁。如图,A、B表示灯塔,暗礁分布在经过A、B两
点的一个圆形区域内,C表示一个危险临界点, ∠ACB
就是“危险角”。当船与两个灯塔的夹角大于“危险角”时,
就有可能触礁。
(1)当船与两个灯塔的夹角大于“危险角”时,
船位于哪个区域?为什么?
(2)当船与两个灯塔的夹角小于“危险角”时,
船位于哪个区域?为什么? ·oα解: (1)当船与两个灯塔的夹角α大于“危险角”时,船位于暗礁区域内( ⊙O内)。理由如下:
①假设船在⊙O上,则∠ α= ∠C,这与∠ α> ∠C矛盾,所以船不可能在⊙O上;
②假设船在⊙O外,如图,则∠ α< ∠AEB, ∠AEB= ∠C,即∠ α< ∠C,这与∠ α> ∠C矛盾,所以船不可能在⊙O外;
综上所述,船只能在⊙O内。 ·oα解: (2)当船与两个灯塔的夹角α小于“危险角”时,船位于暗礁区域外( ⊙O外)。理由如下:
①假设船在⊙O上,则∠ α= ∠C,这与∠ α< ∠C矛盾,所以船不可能在⊙O上;
②假设船在⊙O内,如图,延长AP交⊙O于E,连接BE,则∠E= ∠C。因为 ∠ α> ∠E, 所以∠ α> ∠C,这与∠ α< ∠C矛盾,所以船不可能在⊙O内;ABCEP·Oα综上所述,船只能在⊙O外。 3、如图,AE⊙O的直径, △ABC的顶点都在⊙O上,AD是△ABC的高; 求证:AB · AC = AE · ADAOBCDE综合运用证明:连结BE
∵AE是⊙O的直径,∴∠ABE=90°
∵ AD是△ABC的高,∴∠ADC=90°
∴∠ADC =∠ABE=900,
∠C =∠E
∴△ADC∽ △ABE
∴∴AB · AC = AE · AD能力拓展4、在直径为AB的半圆内划出一块三角形区域,使三角形的一边为AB,顶点C在半圆周上,其他两边分别为6和8,现要建造一个矩形水池DEFN,使D、E在AB上,N在AC上,F在BC上。设计如图所示的方案,其中使AC=8,BC=6。
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x取何值时,水池DEFN的面积最大?最大值是多少?ADGEBNCFM解:(1)(2)设水池DEFN的面积为y
∵NF∥AB
∴△CNF∽△CAB∴当x=2.4时,水池DEFN的面积最大,最大值是12。1、本节课我们学习了哪些知识?
小结圆周角定理的两个推论引辅助线的方法:
(1)构造直径上的圆周角。
(2)构造同弧所对的圆周角。2、本节课我们学习了哪些方法?同步:P52-53作业谢谢莅临指导!
