相似三角形应用(1)

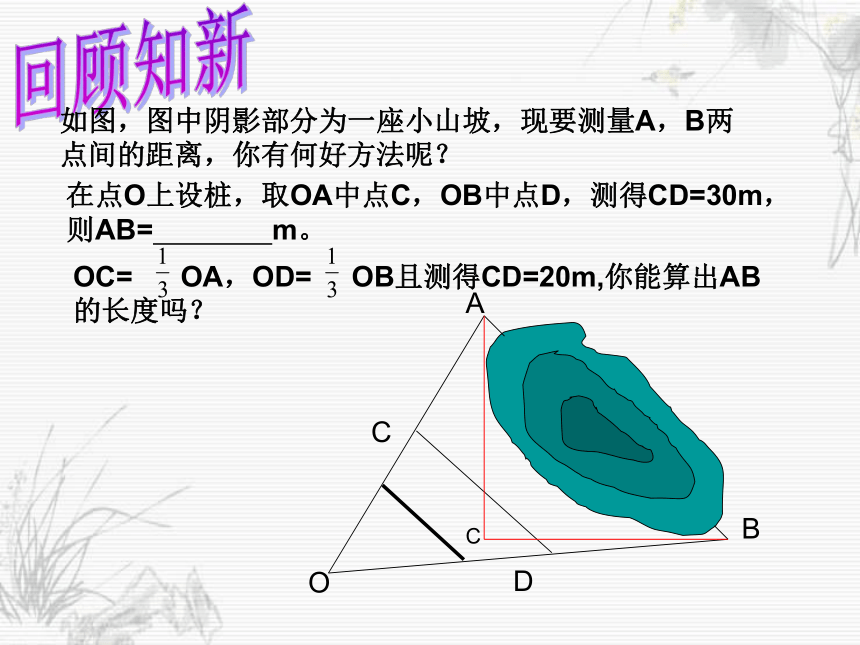
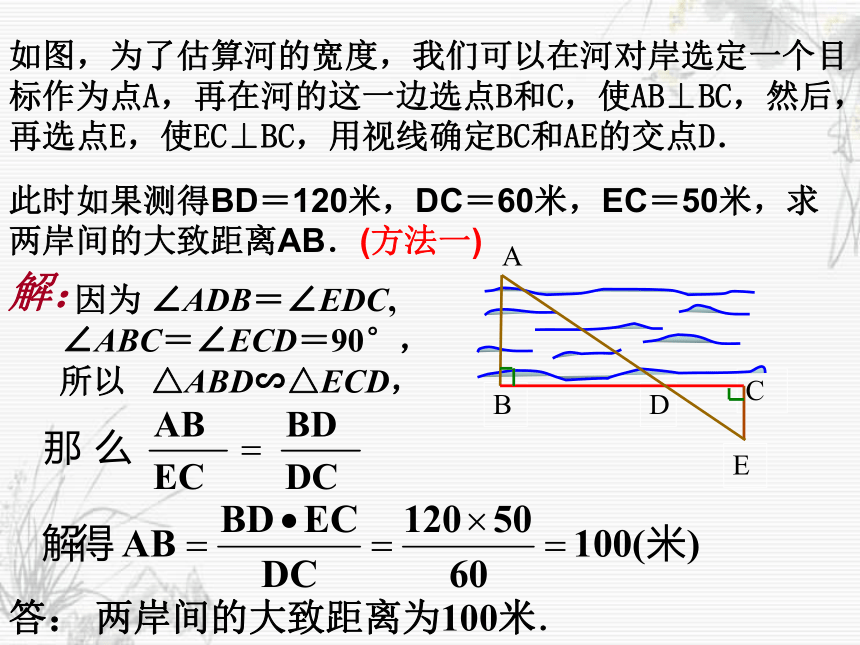
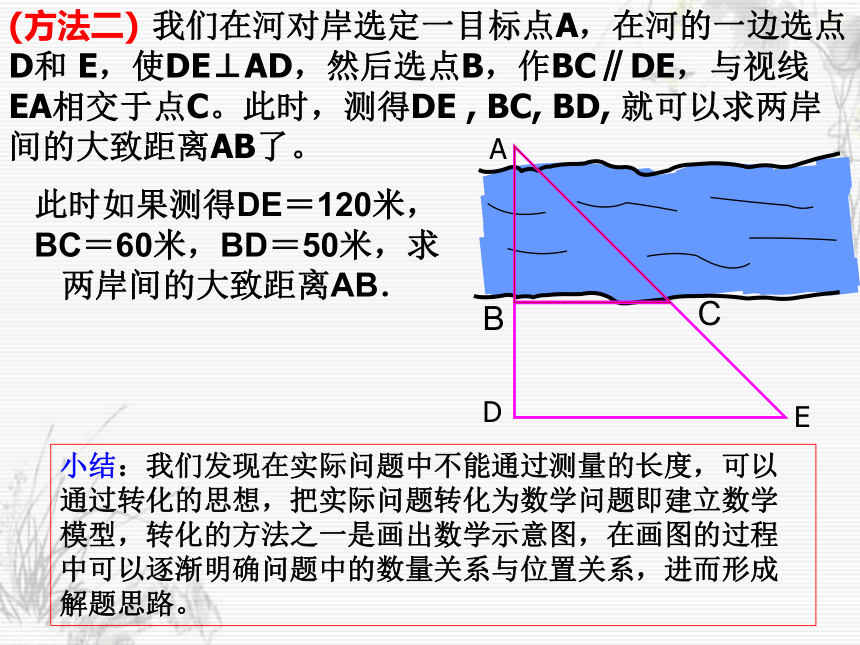
课件16张PPT。27.2.2相似三角形的应用（1） 数学家华罗庚曾经说过：宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，日用之繁，无处不用数学。这是对数学与生活的精彩描述。27.2.2相似三角形的应用（1）回顾知新如图，图中阴影部分为一座小山坡，现要测量A，B两点间的距离，你有何好方法呢？ABOCD在点O上设桩，取OA中点C，OB中点D，测得CD=30m，则AB= m。C如图，为了估算河的宽度，我们可以在河对岸选定一个目标作为点A，再在河的这一边选点B和C，使AB⊥BC，然后，再选点E，使EC⊥BC，用视线确定BC和AE的交点D．?此时如果测得BD＝120米，DC＝60米，EC＝50米，求两岸间的大致距离AB．ADCEB探究一解： 因为 ∠ADB＝∠EDC, ∠ABC＝∠ECD＝90°， ? 所以 △ABD∽△ECD， 答： 两岸间的大致距离为100米． ?此时如果测得BD＝120米，DC＝60米，EC＝50米，求两岸间的大致距离AB．(方法一)如图，为了估算河的宽度，我们可以在河对岸选定一个目标作为点A，再在河的这一边选点B和C，使AB⊥BC，然后，再选点E，使EC⊥BC，用视线确定BC和AE的交点D．?(方法二) 我们在河对岸选定一目标点A，在河的一边选点D和 E，使DE⊥AD，然后选点B，作BC∥DE，与视线EA相交于点C。此时，测得DE , BC, BD, 就可以求两岸间的大致距离AB了。此时如果测得DE＝120米，BC＝60米，BD＝50米，求两岸间的大致距离AB．小结：我们发现在实际问题中不能通过测量的长度，可以通过转化的思想，把实际问题转化为数学问题即建立数学模型，转化的方法之一是画出数学示意图，在画图的过程中可以逐渐明确问题中的数量关系与位置关系，进而形成解题思路。怎样利用相似三角形的有关知识测量旗杆的高度?想一想借太阳的光辉助我们解题,你想到了吗?ABCEDF 若在太阳下旗杆的影长8米，目击者身高1.5米，他在太阳底下的影长2米。此时旗杆高度是多少？ABCDE若在太阳下旗杆的影长AC=8米，目击者身高1.5米，他在太阳底下的影长CD=2米。此时旗杆高度是多少？把一小镜子放在离旗杆（AB）8米的点C处，然后沿着直线BC后退到点D，这时恰好在镜子里看到旗杆顶点B，再用皮尺量得DC=2m，观察者目高DE=1.5m。这时旗杆高多少？你能解决这个问题吗？ABCDE你想到了吗？ABCEFPMN旗杆旁边刚好是一座实验楼，这时旗杆的影子恰好有一部分落在墙上CE=1.5米，地上部分的影子长AC=6米，小明站在旗杆旁边，身高1.5米，影长2米，试问旗杆有多高？练习1.在同一时刻物体的高度与它的影长成正比例.在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为90米,那么高楼的高度是多少米?解：即高楼的高度为54米。因为 在同一时刻物体的高度与它的影长成正比例2、如图，一束平行的光线从教室窗户射入教室的平面示意图，测得光线与地面所成的角∠AMC=30°，窗户的高在教室地面上的影长MN= m，窗户的下檐到教室地面的距离BC=1m(点M、N、C在同一直线上），则窗户的高AB为（ ）ABCNM1你说我说大家说 请你谈谈学习本节课后的感受! 本节课我们学习了利用相似三角形来测量
高度和宽度的方法.
小结数学思想：转化的思想、数学建模的思想