六年级上册数学冀教版4.1探索圆的周长公式课件(共15张PPT)
文档属性
| 名称 | 六年级上册数学冀教版4.1探索圆的周长公式课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-13 08:22:07 | ||
图片预览






文档简介
(共15张PPT)
4.1探索圆的周长公式
课前准备:
一元硬币、有圆面的物品、直尺、线绳
车轮转动一周,谁的车轮走得远?为什么?
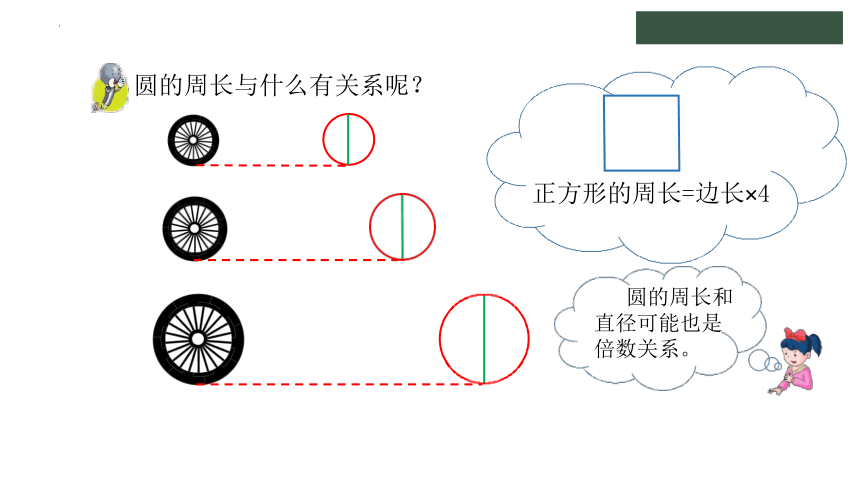
圆的周长与什么有关系呢?
正方形的周长=边长×4
圆的周长和 直径可能也是 倍数关系。
化曲为直
量一量圆的周长和直径。
……
圆是曲线围成的图形,怎样测量它的周长呢?
找一些有圆面的物品,分别测量它们的周长和直径,填在 下表中。(可用计算器计算,除不尽的保留两位小数。)
7.8cm
2.5cm
3.12
9.4cm
3cm
3.13
物品 周长 直径 周长÷直径
一元硬币
自制圆片
饼干桶
37.85cm
12cm
3.15
圆的周长除以直径的商都是三点一几。
圆的周长是直径的3倍多一些。
任意一个圆的周长和直径的商都约是
3.14159,是一个固定不变的数。我们把它叫做
圆周率
母π
C= πd或C= 2 πr
圆周率,用字
π (读作pài)表示。
经过精密计算,人们知道圆周率是一个无 限不循环小数:π =3.141592653……
我们在计算时,一般只取它的近似值(保 留两位小数),即:π≈3.14。
如果用C表示圆的周长,那么
约2000年前,在中国古代的数学著作《周髀算经》 中就有“周三径一”的说法,意思是说,圆的周长约是 直径的三倍。至今,人们还经常用它来估算圆的周长。
约1500年前,中国有一位伟大的科学家祖冲之,他 计算出圆周率应在3.1415926和3.1415927之间,成为世 界上第一个把圆周率的值精确到7位小数的人。这一伟 大成就比欧洲数学家的计算结果至少要早1000年。
π=3.141592653589793238462643383279502884197169
39937510582097494459230781640628620899862803482
53421170679821480865132823066470938446095505822
31725359408128481117450284102701938521105559644
62294895493038196……
一面圆镜的镜面直径是25厘米,在它的边缘镶嵌着一根金属条。
这根金属条的长至少是多少厘米?
C= πd
3.14×25=78.5(厘米)
答:这根金属条的长至少是78.5厘米。
求下面各圆的周长。(单位:厘米)
d=18
r=6
r=1.5
求下面各圆的周长。(单位:厘米)
3.14×18=56.52(厘米)
C= πd
d=18
求下面各圆的周长。(单位:厘米)
2×3.14×6
=6.28×6
=37.68(厘米)
C= 2 πr
r=6
6×2=12(厘米)
3.14×12=37.68(厘米)
C= πd
求下面各圆的周长。(单位:厘米)
r=1.5
C= 2 πr
2×3.14×1.5
=6.28×1.5
=9.42(厘米)
2×3.14×1.5
=2×1.5×3.14
=3×3.14
=9.42(厘米)
回顾总结:
我们经历了猜想、验 证再得出结论的过程。
我们了解到圆周率的历史。
我们可以解决生活中 与圆的周长相关的问题。
4.1探索圆的周长公式
课前准备:
一元硬币、有圆面的物品、直尺、线绳
车轮转动一周,谁的车轮走得远?为什么?
圆的周长与什么有关系呢?
正方形的周长=边长×4
圆的周长和 直径可能也是 倍数关系。
化曲为直
量一量圆的周长和直径。
……
圆是曲线围成的图形,怎样测量它的周长呢?
找一些有圆面的物品,分别测量它们的周长和直径,填在 下表中。(可用计算器计算,除不尽的保留两位小数。)
7.8cm
2.5cm
3.12
9.4cm
3cm
3.13
物品 周长 直径 周长÷直径
一元硬币
自制圆片
饼干桶
37.85cm
12cm
3.15
圆的周长除以直径的商都是三点一几。
圆的周长是直径的3倍多一些。
任意一个圆的周长和直径的商都约是
3.14159,是一个固定不变的数。我们把它叫做
圆周率
母π
C= πd或C= 2 πr
圆周率,用字
π (读作pài)表示。
经过精密计算,人们知道圆周率是一个无 限不循环小数:π =3.141592653……
我们在计算时,一般只取它的近似值(保 留两位小数),即:π≈3.14。
如果用C表示圆的周长,那么
约2000年前,在中国古代的数学著作《周髀算经》 中就有“周三径一”的说法,意思是说,圆的周长约是 直径的三倍。至今,人们还经常用它来估算圆的周长。
约1500年前,中国有一位伟大的科学家祖冲之,他 计算出圆周率应在3.1415926和3.1415927之间,成为世 界上第一个把圆周率的值精确到7位小数的人。这一伟 大成就比欧洲数学家的计算结果至少要早1000年。
π=3.141592653589793238462643383279502884197169
39937510582097494459230781640628620899862803482
53421170679821480865132823066470938446095505822
31725359408128481117450284102701938521105559644
62294895493038196……
一面圆镜的镜面直径是25厘米,在它的边缘镶嵌着一根金属条。
这根金属条的长至少是多少厘米?
C= πd
3.14×25=78.5(厘米)
答:这根金属条的长至少是78.5厘米。
求下面各圆的周长。(单位:厘米)
d=18
r=6
r=1.5
求下面各圆的周长。(单位:厘米)
3.14×18=56.52(厘米)
C= πd
d=18
求下面各圆的周长。(单位:厘米)
2×3.14×6
=6.28×6
=37.68(厘米)
C= 2 πr
r=6
6×2=12(厘米)
3.14×12=37.68(厘米)
C= πd
求下面各圆的周长。(单位:厘米)
r=1.5
C= 2 πr
2×3.14×1.5
=6.28×1.5
=9.42(厘米)
2×3.14×1.5
=2×1.5×3.14
=3×3.14
=9.42(厘米)
回顾总结:
我们经历了猜想、验 证再得出结论的过程。
我们了解到圆周率的历史。
我们可以解决生活中 与圆的周长相关的问题。
