2009金华市初中数学学业考试试题特征研究及复习建议
文档属性
| 名称 | 2009金华市初中数学学业考试试题特征研究及复习建议 |  | |
| 格式 | rar | ||
| 文件大小 | 22.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-24 19:36:00 | ||
图片预览








文档简介
课件23张PPT。数学学业考试试题特征
研究及复习建议义乌市教育局教研室1、2008年数学学业考试试题总体特征
2、2008年数学学业考试试题分项特征
3、欣赏学业考试卷,聚焦压轴题
4、由一堂复习课想到的几个问题-浅谈复习 如果把04至05年称为是学业试卷的起步期,这一期间学业试卷从形式、内容、难度上都处于探索的初级阶段,尚未形成成熟的学业试卷风格;则06至07年为发展期,这一期间学业试卷变化较大,试卷的创新力度很大,出现了一些既符合学生实际又有强烈的新课标气息、鼓励学生发展个性、发展学生创新能力的各种新题型,发展期的学业试卷充满朝气、富有创意,令人耳目一新;那么我们可以说08年学业试卷则步入稳定期, 08年学业试卷步入稳定期,形成了“注重基础;突出课改;能力立卷;稳中求新” 四大特征 (一)、学业考试发展轨迹回顾(二)、2008年数学学业考试试题四大特征分析1、注重基础
(1)在试卷形式上为试题起点低,有足够的送分题
(2)结构合理。难题不是难在方法技巧、知识生僻上,而是难在思维的灵活性与深度上。
(3)控制难度。
(4)基础的知识点单独考查,相对综合题,单项考查某一知识点的得分显然更高。
(5)分层考查不同认知水平的同一重要知识点。
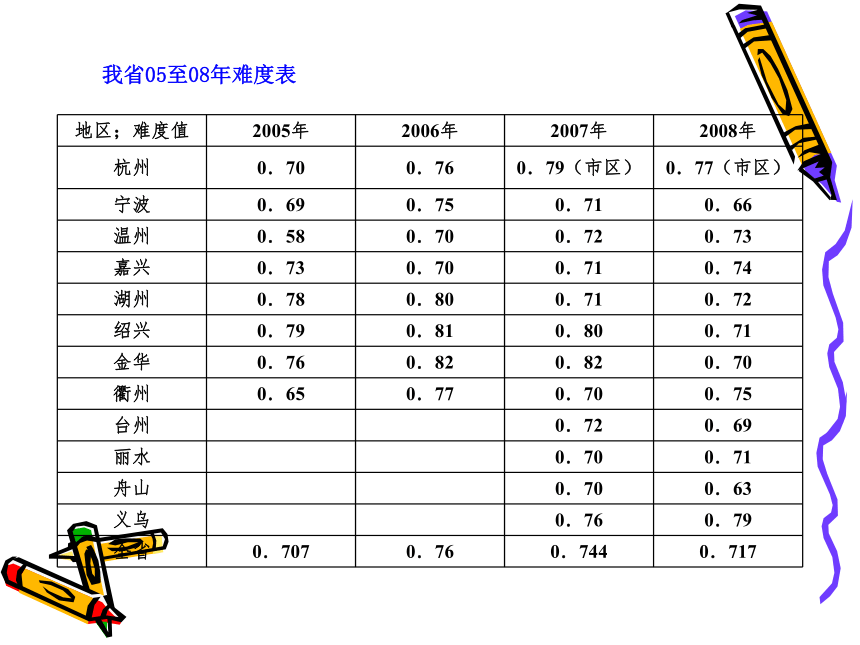
(6)创设一些知识链型试题,以增强试题关联性。我省05至08年难度表 学业考卷一般通过以下五种途径来调控难度一、降低起点;
二、增加容易题;
三、控制试题阅读量。
四、不出怪题、偏题、技巧性强的题
五、根据当地学生实际情况量身定做设计试题。人文性
背景公正性
时代性、思想性
开放性、探究性 2、突出课改(1)主要的数学思想方法突出考查。
(2)注重考查知识的联系与渗透,体现数学活动过程。
(3)探究能力,思维发散能力,创新能力,应用数学知识解决问题的能力仍然是诸多考查能力中的考查重点3、能力立卷结构合理
保持稳定
力求创新4、稳中求新浙江省各地级市2008年试题类型分布表 (平均值) 浙江省各地级市2007年试题类型分布表 (平均值) 第一部分 数与代数的考法分析
第二部分 空间与图形的考法分析
第三部分 统计与概率的考法分析
第四部分 数学学习能力的考法分析二、2008年数学学业考试试题分项特征第一部分 数与代数的考法分析一、“数与式”考法分析
1、注重对“数与式”的有关概念和性质的考查。
2、加强对“数与式”运算的考查
3、加大对“数与式”表达功能的考查
数与式的本质意义是表示事物和过程中的数量和数量关系,这也是“数感”、“符号感”的核心体现,
⑴直接列式表达情景中的数量或数量关系(衢州4)
⑵借助图形直观考查列式表达数量关系(湖州18)
⑶通过估算的方式考查列式表达数量(杭州10)
⑷用代数式表示变化规律(金华16)二、“方程与不等式”的考法分析
1、考查方程和不等式的有关概念和解法
⑴直接考查方程与不等式的有关知识(宁波20)
⑵灵活考查方程与不等式的解法(义乌21)
2、考查列方程的能力(杭州9)
3、考查方程与不等式的应用和方程思想
⑴方程与不等式的一般应用(绍兴19)
⑵方程与不等式的综合应用(衢州23)三、“函数”的考法分析
㈠内容特点分析
㈡考法分析
1、直接考查函数的有关概念和性质(温州5)
2、灵活考查函数关系式的建立和转化能力
⑴考查对函数图象的理解(丽水9)
⑵考查利用图象表达函数关系的能力(金华10)
⑶考查对函数表达形式之间的转化能力(杭州18)
3、综合考查函数、方程与不等式之间的联系(嘉兴10)
4、灵活运用函数知识和思想方法解决问题
⑴解决几何中的最值问题(衢州24)
⑵解决以函数知识为背景的具有实际背景的问题(义乌24)
⑶解决具有实际背景的问题(衢州23)
一、“相交线与平行线”的考法分析
1、注重考查平行线的判定和性质(杭州4)
2、突出考查平行线的性质在综合问题中的应用(宁波4)
二、“三角形”的考法分析
1、注重从多角度考查三角形的有关性质(丽水8)
2、突出考查三角形的全等关系(义乌24)
3、重点考查三角形与相关知识间的联系(金华24)
三、“四边形”的考法分析
1、普遍注意对四边形基本性质的考查(台州6)
2、注重四边形与图形变换的结合与应用(绍兴3)
3、突出对四边形中推理能力的综合考查(湖州20) 第二部分 空间与图形的考法分析四、“圆”的考法分析
㈠内容特点的分析
㈡考法分析
1、重点考查圆的有关概念和性质(金华7、21)
2、突出从多角度考查与圆有关的计算问题(义乌20、杭州9)(见链接)
五、“视图与投影”的考法分析
1、注重适当考查空间观念
2、重视适度考查平行投影(金华6)(见链接)
六、“轴对称、平移与旋转”的考法分析
1、注重考查对变换性质的理解和运用(绍兴8)
2、强化考查变换在推理论证中的工具作用(义乌22)(见链接)
七、“相似形”的考法分析
㈠内容特点分析
㈡考法分析
1、简单考查相似多边形的性质(宁波16)
2、灵活考查相似三角形的判定和性质(绍兴24)
3、综合考查相似三角形与其他知识的联系(台州24)(见链接)
八、“锐角三角函数”的考法分析
1、关注对锐角三角函数定义的考查(温州7)
2、突出考查解直角三角形在实际问题中的应用(绍兴19)(见链接)
九、“图形与坐标”的考法分析
1、重视对图形与坐标对应关系的理解与应用(杭州3)
2、关注图形与坐标的综合应用(宁波23)(见链接)
十、“图形与证明”的考法分析
1、单独对合情推理与演绎推理能力考查(金华18)
2、突出对合情推理与演绎推理能力的综合考查(衢州20)
3、重视对合情推理与演绎推理能力较高水平的考查(台州23)
第三部分 统计与概率的考法分析一、“统计”的考法分析
㈠内容特点分析
㈡考法分析
1、结合具体调查问题,考查抽样意识。
2、通过观察、比较、综合等方式考查读图、释图、作图和评图能力。
3、变换考查视角,突出对统计计量本质的考查。
二、“概率”的考法分析
㈠内容特点分析
㈡考法分析
1、直接考查概率的有关基本概念。
2、结合变化多样的问题背景和问题表征形式,考查计算简单随机事件概率的能力。
3、通过模似试验,考查用频率估计概率的思想。一、通过对已学知识掌握的概括化程度来考查学生的数学学习能力。
二、通过在已学知识基础上做深入化探究和拓展性探究来考查学生的数学学习能力。
㈠做深入化探究
1、探究“存在性”
2、探究特殊结论或特殊条件
㈡做拓展性研究
1、探索不变性
2、探索“变化规律”
三、设置学习与应用新知识或掌握与运用一般性方法考查学生的数学学习能
㈠设置“新知识”学习与应用过程
㈡突出一个具有“一般性方法”意义的探究过程第四部分 数学学习能力的考法分析三、欣赏学业考试卷,聚焦压轴题评价原则: (1) 导向性;(2)科学性;(3)一致性;(4)积极性;(5)有效性 (一)欣赏2008年杭州中考卷 (二)重点分析两类题型函数动态压轴题强势依旧,如日中天,红遍大江南北;折叠题型千姿百态,大放异彩;几何探究题方兴未艾。图形的运动 关键在于做到“静中思变”、“动中求静”,以揭示问题的本质。以静制动。找出动态中的相对不变,是解决问题的重点。 折叠题 (1) 对称轴;(2) 全等; (3) 相似; (4) 根据题意建立函数关系即建立方程模型。 问题:
(1) 教师在复习中听处的地位及作用;
(2) 如何突出学生的主体地位。
1、把握“双纲”,以教材为本,明确复习方向。
2、夯实基础,降低复习重心,面向全体。
3、注重复习的整体设计,构建知识网络。
4. 注重思维训练、重视思想方法,着眼于发展数学能力
5、精选题型,查漏补缺,对症下药。
6、注重发展学生的数学应用意识和实践能力。由一堂复习课想到的几个问题-浅谈复习谢 谢!
2、2008年数学学业考试试题分项特征
3、欣赏学业考试卷,聚焦压轴题
4、由一堂复习课想到的几个问题-浅谈复习 如果把04至05年称为是学业试卷的起步期,这一期间学业试卷从形式、内容、难度上都处于探索的初级阶段,尚未形成成熟的学业试卷风格;则06至07年为发展期,这一期间学业试卷变化较大,试卷的创新力度很大,出现了一些既符合学生实际又有强烈的新课标气息、鼓励学生发展个性、发展学生创新能力的各种新题型,发展期的学业试卷充满朝气、富有创意,令人耳目一新;那么我们可以说08年学业试卷则步入稳定期, 08年学业试卷步入稳定期,形成了“注重基础;突出课改;能力立卷;稳中求新” 四大特征 (一)、学业考试发展轨迹回顾(二)、2008年数学学业考试试题四大特征分析1、注重基础
(1)在试卷形式上为试题起点低,有足够的送分题
(2)结构合理。难题不是难在方法技巧、知识生僻上,而是难在思维的灵活性与深度上。
(3)控制难度。
(4)基础的知识点单独考查,相对综合题,单项考查某一知识点的得分显然更高。
(5)分层考查不同认知水平的同一重要知识点。
(6)创设一些知识链型试题,以增强试题关联性。我省05至08年难度表 学业考卷一般通过以下五种途径来调控难度一、降低起点;
二、增加容易题;
三、控制试题阅读量。
四、不出怪题、偏题、技巧性强的题
五、根据当地学生实际情况量身定做设计试题。人文性
背景公正性
时代性、思想性
开放性、探究性 2、突出课改(1)主要的数学思想方法突出考查。
(2)注重考查知识的联系与渗透,体现数学活动过程。
(3)探究能力,思维发散能力,创新能力,应用数学知识解决问题的能力仍然是诸多考查能力中的考查重点3、能力立卷结构合理
保持稳定
力求创新4、稳中求新浙江省各地级市2008年试题类型分布表 (平均值) 浙江省各地级市2007年试题类型分布表 (平均值) 第一部分 数与代数的考法分析
第二部分 空间与图形的考法分析
第三部分 统计与概率的考法分析
第四部分 数学学习能力的考法分析二、2008年数学学业考试试题分项特征第一部分 数与代数的考法分析一、“数与式”考法分析
1、注重对“数与式”的有关概念和性质的考查。
2、加强对“数与式”运算的考查
3、加大对“数与式”表达功能的考查
数与式的本质意义是表示事物和过程中的数量和数量关系,这也是“数感”、“符号感”的核心体现,
⑴直接列式表达情景中的数量或数量关系(衢州4)
⑵借助图形直观考查列式表达数量关系(湖州18)
⑶通过估算的方式考查列式表达数量(杭州10)
⑷用代数式表示变化规律(金华16)二、“方程与不等式”的考法分析
1、考查方程和不等式的有关概念和解法
⑴直接考查方程与不等式的有关知识(宁波20)
⑵灵活考查方程与不等式的解法(义乌21)
2、考查列方程的能力(杭州9)
3、考查方程与不等式的应用和方程思想
⑴方程与不等式的一般应用(绍兴19)
⑵方程与不等式的综合应用(衢州23)三、“函数”的考法分析
㈠内容特点分析
㈡考法分析
1、直接考查函数的有关概念和性质(温州5)
2、灵活考查函数关系式的建立和转化能力
⑴考查对函数图象的理解(丽水9)
⑵考查利用图象表达函数关系的能力(金华10)
⑶考查对函数表达形式之间的转化能力(杭州18)
3、综合考查函数、方程与不等式之间的联系(嘉兴10)
4、灵活运用函数知识和思想方法解决问题
⑴解决几何中的最值问题(衢州24)
⑵解决以函数知识为背景的具有实际背景的问题(义乌24)
⑶解决具有实际背景的问题(衢州23)
一、“相交线与平行线”的考法分析
1、注重考查平行线的判定和性质(杭州4)
2、突出考查平行线的性质在综合问题中的应用(宁波4)
二、“三角形”的考法分析
1、注重从多角度考查三角形的有关性质(丽水8)
2、突出考查三角形的全等关系(义乌24)
3、重点考查三角形与相关知识间的联系(金华24)
三、“四边形”的考法分析
1、普遍注意对四边形基本性质的考查(台州6)
2、注重四边形与图形变换的结合与应用(绍兴3)
3、突出对四边形中推理能力的综合考查(湖州20) 第二部分 空间与图形的考法分析四、“圆”的考法分析
㈠内容特点的分析
㈡考法分析
1、重点考查圆的有关概念和性质(金华7、21)
2、突出从多角度考查与圆有关的计算问题(义乌20、杭州9)(见链接)
五、“视图与投影”的考法分析
1、注重适当考查空间观念
2、重视适度考查平行投影(金华6)(见链接)
六、“轴对称、平移与旋转”的考法分析
1、注重考查对变换性质的理解和运用(绍兴8)
2、强化考查变换在推理论证中的工具作用(义乌22)(见链接)
七、“相似形”的考法分析
㈠内容特点分析
㈡考法分析
1、简单考查相似多边形的性质(宁波16)
2、灵活考查相似三角形的判定和性质(绍兴24)
3、综合考查相似三角形与其他知识的联系(台州24)(见链接)
八、“锐角三角函数”的考法分析
1、关注对锐角三角函数定义的考查(温州7)
2、突出考查解直角三角形在实际问题中的应用(绍兴19)(见链接)
九、“图形与坐标”的考法分析
1、重视对图形与坐标对应关系的理解与应用(杭州3)
2、关注图形与坐标的综合应用(宁波23)(见链接)
十、“图形与证明”的考法分析
1、单独对合情推理与演绎推理能力考查(金华18)
2、突出对合情推理与演绎推理能力的综合考查(衢州20)
3、重视对合情推理与演绎推理能力较高水平的考查(台州23)
第三部分 统计与概率的考法分析一、“统计”的考法分析
㈠内容特点分析
㈡考法分析
1、结合具体调查问题,考查抽样意识。
2、通过观察、比较、综合等方式考查读图、释图、作图和评图能力。
3、变换考查视角,突出对统计计量本质的考查。
二、“概率”的考法分析
㈠内容特点分析
㈡考法分析
1、直接考查概率的有关基本概念。
2、结合变化多样的问题背景和问题表征形式,考查计算简单随机事件概率的能力。
3、通过模似试验,考查用频率估计概率的思想。一、通过对已学知识掌握的概括化程度来考查学生的数学学习能力。
二、通过在已学知识基础上做深入化探究和拓展性探究来考查学生的数学学习能力。
㈠做深入化探究
1、探究“存在性”
2、探究特殊结论或特殊条件
㈡做拓展性研究
1、探索不变性
2、探索“变化规律”
三、设置学习与应用新知识或掌握与运用一般性方法考查学生的数学学习能
㈠设置“新知识”学习与应用过程
㈡突出一个具有“一般性方法”意义的探究过程第四部分 数学学习能力的考法分析三、欣赏学业考试卷,聚焦压轴题评价原则: (1) 导向性;(2)科学性;(3)一致性;(4)积极性;(5)有效性 (一)欣赏2008年杭州中考卷 (二)重点分析两类题型函数动态压轴题强势依旧,如日中天,红遍大江南北;折叠题型千姿百态,大放异彩;几何探究题方兴未艾。图形的运动 关键在于做到“静中思变”、“动中求静”,以揭示问题的本质。以静制动。找出动态中的相对不变,是解决问题的重点。 折叠题 (1) 对称轴;(2) 全等; (3) 相似; (4) 根据题意建立函数关系即建立方程模型。 问题:
(1) 教师在复习中听处的地位及作用;
(2) 如何突出学生的主体地位。
1、把握“双纲”,以教材为本,明确复习方向。
2、夯实基础,降低复习重心,面向全体。
3、注重复习的整体设计,构建知识网络。
4. 注重思维训练、重视思想方法,着眼于发展数学能力
5、精选题型,查漏补缺,对症下药。
6、注重发展学生的数学应用意识和实践能力。由一堂复习课想到的几个问题-浅谈复习谢 谢!
同课章节目录
