苏教版五年级下册数学8.5整理与复习应用广角课件(共18张PPT)
文档属性
| 名称 | 苏教版五年级下册数学8.5整理与复习应用广角课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-13 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
整理与复习
应用广角
八
苏教版数学五年级(下)
转化是怎样的策略?
转化是把要解决的新问题,变成已经能解决的问题,获得解决问题的思路和方法的策略。
课堂导入
1.有些不规则的图形可以转化成熟悉的简单的图形。图形转化时可以运用平移、旋转等方法。转化后的图形与转化前相比,形状变了,面积没有变。
2.应用转化的策略能使问题化繁为简,化未知为已知。
不规则图形的面积
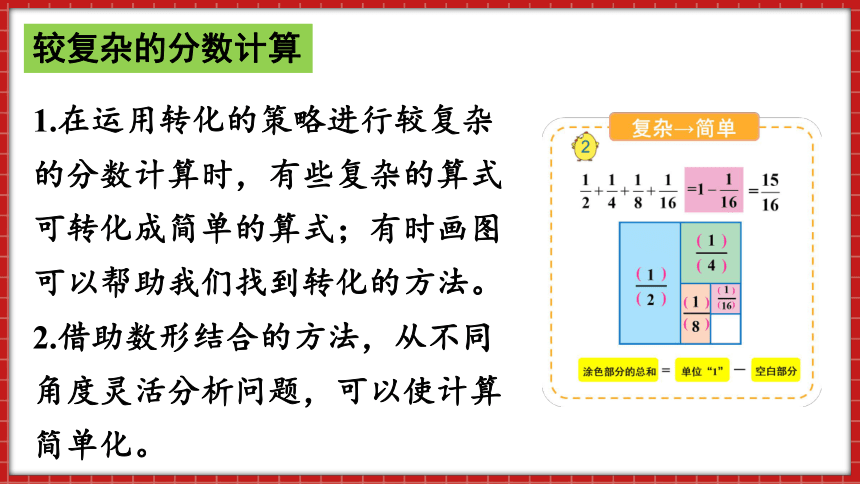
1.在运用转化的策略进行较复杂的分数计算时,有些复杂的算式可转化成简单的算式;有时画图可以帮助我们找到转化的方法。
2.借助数形结合的方法,从不同角度灵活分析问题,可以使计算简单化。
较复杂的分数计算
1. 如图,这些车轮的形状为什么设计成圆形?
圆心到圆上任意一点的
距离都相同,车轮设计
成圆形,可以保持车轮
圆心到地面的距离不变,
使车辆平稳行驶。(理由合理即可)
课堂练习
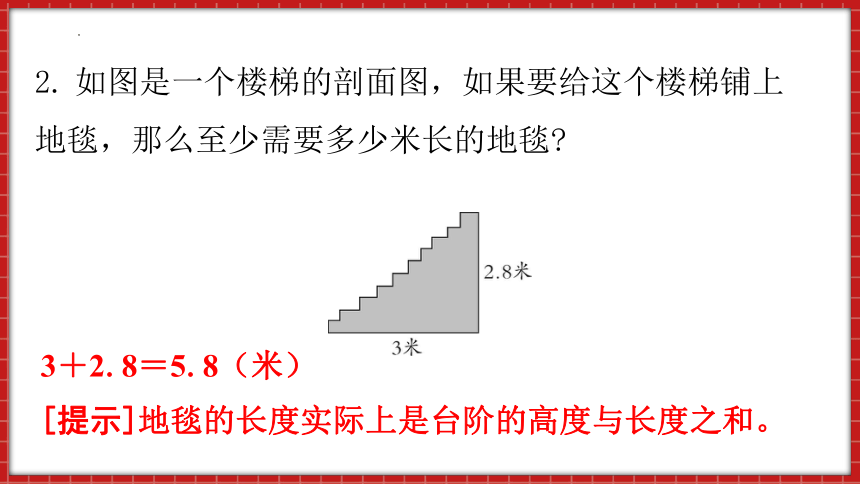
2. 如图是一个楼梯的剖面图,如果要给这个楼梯铺上地毯,那么至少需要多少米长的地毯
3+2.8=5.8(米)
[提示]地毯的长度实际上是台阶的高度与长度之和。
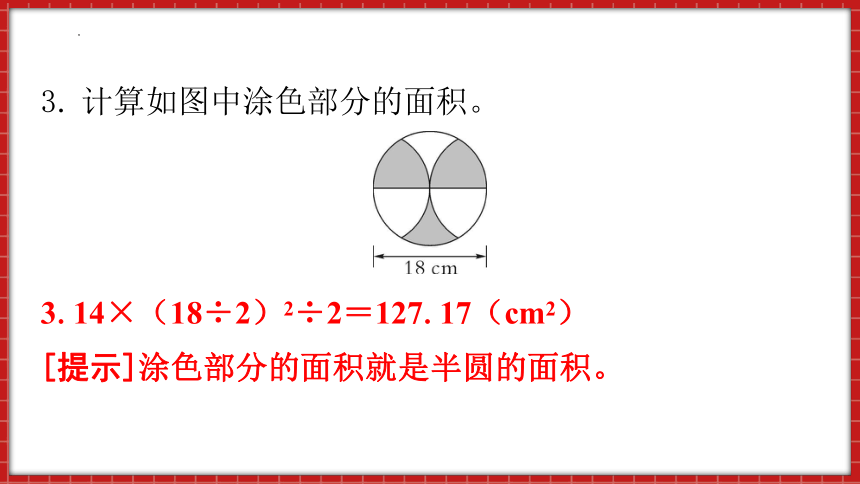
3. 计算如图中涂色部分的面积。
3.14×(18÷2)2÷2=127.17(cm2)
[提示]涂色部分的面积就是半圆的面积。
归纳总结:运用数形结合思想,将复杂算式的求和转化为“1”与另一个数的差来计算,复杂的算式用直观形象的图形表示出来,会使计算更简便。
4.计算:
5.某公园内一个近似圆形的湖面,直径大约为1000米。
(1)沿湖的一周每隔5米栽1棵柳树,一共可以栽多少棵
柳树?
3.14×1000÷5=628(棵)
答:一共可以栽628棵柳树。
(2)若在湖里养鱼,按每100平方米养60条鱼计算,则湖里一
共可以养多少条鱼?
3.14×(1000÷2)2÷100×60=471000(条)
答:湖里一共可以养471000条鱼。
6. 有一堆钢管,最上面一层有5根,最下面一层有11根,每相邻两层的钢管数量都相差2根。这堆钢管一共有多少根
(11-5)÷2+1=4(层)
(5+11)×4÷2=32(根)
7. 在一个长是4分米、宽是1分米的长方形中画一个最大的半圆。半圆的面积是多少平方分米
3.14×12÷2=1.57(平方分米)
8. 周日梦梦从家里出发去蓝蓝家做客。梦梦出发6 分钟后妈妈发现梦梦忘记带送给蓝蓝的礼物,于是立刻去追梦梦。妈妈的速度是80 米/ 分,妈妈追上梦梦用了9 分钟。梦梦的速度是多少?
解:设梦梦的速度是x 米/ 分。
6x+9x=80×9
x=48
答:梦梦的速度是48 米/ 分。
9. 某商场休息区安放了一组休息椅,表面宽度均相同,如图所示,这组休息椅椅面的面积是多少平方米?
1+0.5=1.5(m)
(3.14×1.52-3.14×0.52 ) ÷2×3=9.42(m2 )
答:这组休息椅椅面的面积是9.42 m2。
10.郝佳摆了一个干果盘(如图)。摆瓜子的面积占果盘面
积的,摆花生的面积占果盘面积的。
(1)摆开心果的面积占果盘面积的几分之几?
(2)如果果盘的半径是10厘米,摆花生的面积大约是多少
平方厘米? (得数保留整数)
(1)摆开心果的面积占果盘面积的几分之几?
1--=
答:摆开心果的面积占果盘面积的。
(2)如果果盘的半径是10厘米,摆花生的面积大约是多少
平方厘米? (得数保留整数)
3.14×102÷8×3≈118(平方厘米)
答:摆花生的面积大约是118平方厘米。
1.如图,有一个长方形绿化广场,长20 m、宽15 m,中间有一
条宽为2 m的小路,求绿化带(涂色部分)的面积。
(20-2)×(15-2)=234(m2)
答:绿化带(涂色部分)的面积是234 m2。
思维拓展
2. 如图是某电车从A 站出发经过B 站到达C站,然后原路返回A 站的行驶情况,去时在B 站停车,而返回时不停,去时的车速为0.5 km/min,求该电车往返的平均速度。(停车时间除外)
(10-1)×0.5×2=9(km)
9÷(15-1)= (km/min)
答:该电车往返的平均速度是km/min。
整理与复习
应用广角
八
苏教版数学五年级(下)
转化是怎样的策略?
转化是把要解决的新问题,变成已经能解决的问题,获得解决问题的思路和方法的策略。
课堂导入
1.有些不规则的图形可以转化成熟悉的简单的图形。图形转化时可以运用平移、旋转等方法。转化后的图形与转化前相比,形状变了,面积没有变。
2.应用转化的策略能使问题化繁为简,化未知为已知。
不规则图形的面积
1.在运用转化的策略进行较复杂的分数计算时,有些复杂的算式可转化成简单的算式;有时画图可以帮助我们找到转化的方法。
2.借助数形结合的方法,从不同角度灵活分析问题,可以使计算简单化。
较复杂的分数计算
1. 如图,这些车轮的形状为什么设计成圆形?
圆心到圆上任意一点的
距离都相同,车轮设计
成圆形,可以保持车轮
圆心到地面的距离不变,
使车辆平稳行驶。(理由合理即可)
课堂练习
2. 如图是一个楼梯的剖面图,如果要给这个楼梯铺上地毯,那么至少需要多少米长的地毯
3+2.8=5.8(米)
[提示]地毯的长度实际上是台阶的高度与长度之和。
3. 计算如图中涂色部分的面积。
3.14×(18÷2)2÷2=127.17(cm2)
[提示]涂色部分的面积就是半圆的面积。
归纳总结:运用数形结合思想,将复杂算式的求和转化为“1”与另一个数的差来计算,复杂的算式用直观形象的图形表示出来,会使计算更简便。
4.计算:
5.某公园内一个近似圆形的湖面,直径大约为1000米。
(1)沿湖的一周每隔5米栽1棵柳树,一共可以栽多少棵
柳树?
3.14×1000÷5=628(棵)
答:一共可以栽628棵柳树。
(2)若在湖里养鱼,按每100平方米养60条鱼计算,则湖里一
共可以养多少条鱼?
3.14×(1000÷2)2÷100×60=471000(条)
答:湖里一共可以养471000条鱼。
6. 有一堆钢管,最上面一层有5根,最下面一层有11根,每相邻两层的钢管数量都相差2根。这堆钢管一共有多少根
(11-5)÷2+1=4(层)
(5+11)×4÷2=32(根)
7. 在一个长是4分米、宽是1分米的长方形中画一个最大的半圆。半圆的面积是多少平方分米
3.14×12÷2=1.57(平方分米)
8. 周日梦梦从家里出发去蓝蓝家做客。梦梦出发6 分钟后妈妈发现梦梦忘记带送给蓝蓝的礼物,于是立刻去追梦梦。妈妈的速度是80 米/ 分,妈妈追上梦梦用了9 分钟。梦梦的速度是多少?
解:设梦梦的速度是x 米/ 分。
6x+9x=80×9
x=48
答:梦梦的速度是48 米/ 分。
9. 某商场休息区安放了一组休息椅,表面宽度均相同,如图所示,这组休息椅椅面的面积是多少平方米?
1+0.5=1.5(m)
(3.14×1.52-3.14×0.52 ) ÷2×3=9.42(m2 )
答:这组休息椅椅面的面积是9.42 m2。
10.郝佳摆了一个干果盘(如图)。摆瓜子的面积占果盘面
积的,摆花生的面积占果盘面积的。
(1)摆开心果的面积占果盘面积的几分之几?
(2)如果果盘的半径是10厘米,摆花生的面积大约是多少
平方厘米? (得数保留整数)
(1)摆开心果的面积占果盘面积的几分之几?
1--=
答:摆开心果的面积占果盘面积的。
(2)如果果盘的半径是10厘米,摆花生的面积大约是多少
平方厘米? (得数保留整数)
3.14×102÷8×3≈118(平方厘米)
答:摆花生的面积大约是118平方厘米。
1.如图,有一个长方形绿化广场,长20 m、宽15 m,中间有一
条宽为2 m的小路,求绿化带(涂色部分)的面积。
(20-2)×(15-2)=234(m2)
答:绿化带(涂色部分)的面积是234 m2。
思维拓展
2. 如图是某电车从A 站出发经过B 站到达C站,然后原路返回A 站的行驶情况,去时在B 站停车,而返回时不停,去时的车速为0.5 km/min,求该电车往返的平均速度。(停车时间除外)
(10-1)×0.5×2=9(km)
9÷(15-1)= (km/min)
答:该电车往返的平均速度是km/min。
