第三章 圆单元测试卷A(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版九年级数学下册《圆》测试卷A
满分:120分 考试时间:90分钟
选择题。(每小题3分,共30分)
1. 已知⊙O的直径是6,点O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
2. 下列说法中正确的是( )
A.垂直于半径的直线是圆的切线 B.圆的切线垂直于半径
C.经过半径的外端的直线是圆的切线 D.圆的切线垂直于过切点的半径
3. 如图,四边形ABCD内接于☉O,AC平分∠BAD,则下列结论中正确的是 ( )
A. AB=AD B. BC=CD C.= D. ∠BCA=∠ACD
4.如果两个圆心角相等,那么( )
A.这两个圆心角所对的弦相等 B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等 D.以上说法都不对
5.如图,点A,B,C在⊙O上,∠BAC=54°,则∠BOC的度数为( )
A.27° B.108° C.116° D.128°
第3题 第5题 第6题
6.如图,AB是⊙O的直径,==,∠COD=38°,则∠AEO的度数是( )
A.52° B.57° C.66° D.78°
7.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于( )
A.20° B.30° C.40° D.50°
8.同一个圆的内接正六边形和外切正六边形的周长之比为( )
A.3∶4 B.∶2 C.2∶ D.1∶2
第7题 第9题 第10题
9.如图,PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E,交AB于点C.下列结论:①PA=PB;②AC=BC;③OC=CD;④PA·AC=PC·AO.其中正确的有( )
A.①③④ B.②③④ C.①②③ D.①②④
如图,在等边△ABC中,AB=6,点D,E分别在边BC,AC上,且BD=CE,连接AD,BE交于点F,连接CF,则CF的最小值是( )
A.3 B.2 C.4 D.3
填空题(每小题4分共28分)
11.如图,在⊙O中,=,∠A=40°,则∠B=________.
(第11题) (第12题) (第13题)
12.如图,已知△ABC的内切圆⊙O与BC边相切于点D,连接OB,OD.若∠ABC=40°,则∠BOD的度数是________.
13.如图,⊙P的半径为2,P在函数y=(x>0)的图象上运动,当⊙P与x轴相切时,点P的坐标为__________.
14. 如图,∠APB=30°,圆心在PB上的⊙O的半径为1 cm,OP=3 cm,若⊙O沿BP方向平移,当⊙O与直线PA相切时,圆心O平移的距离为____________.
第14题 第15题 第16题
15.如图,一条公路的转弯处是一段圆弧(图中的),点O是这段弧的圆心,C是上一点,OC⊥AB,垂足为D,AB=160m,CD=40m,则这段弯路的半径是 m.
16.如图,在⊙O中,AB是⊙O的直径,AB=8 cm, ==,M是 AB上一动点,CM+DM的最小值是__ __cm.
17.如图,在平面直角坐标系中,以点A(0,2)为圆心,2为半径的圆交y轴于点B.已知点C(2,0),点D为⊙A上的一动点,以CD为斜边,在CD左侧作等腰直角三角形CDE,连接BC,则△BCE面积的最小值为 .
解答题(6×3=18分)
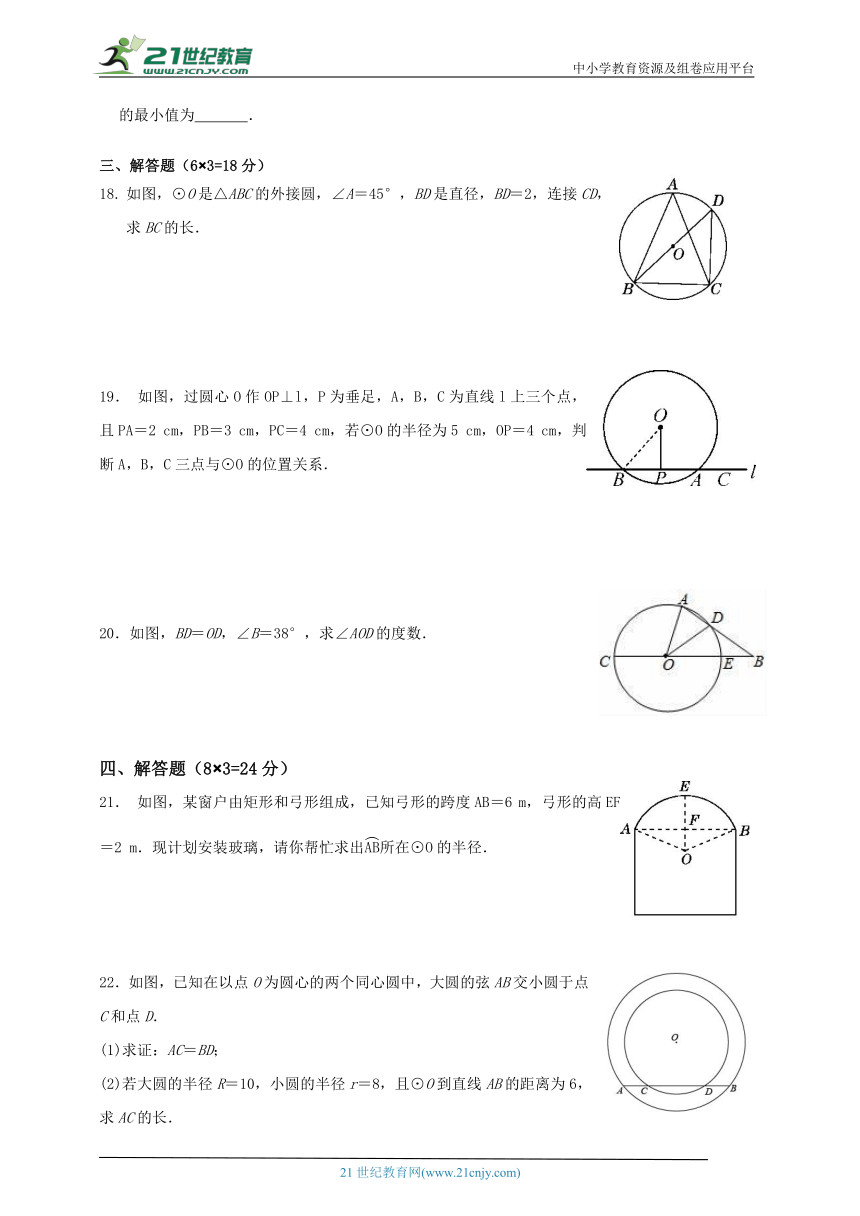
如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,BD=2,连接CD,求BC的长.
19. 如图,过圆心O作OP⊥l,P为垂足,A,B,C为直线l上三个点,且PA=2 cm,PB=3 cm,PC=4 cm,若⊙O的半径为5 cm,OP=4 cm,判断A,B,C三点与⊙O的位置关系.
20.如图,BD=OD,∠B=38°,求∠AOD的度数.
解答题(8×3=24分)
21. 如图,某窗户由矩形和弓形组成,已知弓形的跨度AB=6 m,弓形的高EF=2 m.现计划安装玻璃,请你帮忙求出所在⊙O的半径.
22.如图,已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C和点D.
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且⊙O到直线AB的距离为6,求AC的长.
23.如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,连接AC,若CA=CP,∠A=30°.
(1)求证:CP是⊙O的切线;
(2)若OA=1,求弦AC的长.
解答题 (10×2=20分)
如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,
AE交⊙O于点B,且AB=OC.
(1)求∠AOB的度数.
(2)求∠EOD的度数.
25.( 如图,半圆O的直径DE=12 cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=12 cm.半圆O以2 cm/s的速度自左向右运动,在运动过程中,点D,E始终在直线BC上.设运动时间为t s,当t=0时,半圆O在△ABC的左侧,OC=8 cm.
(1)当t=________时,半圆O与AC所在直线第一次相切;点C到直线AB的距离为________.
(2)当t为何值时,直线AB与半圆O所在的圆相切?
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B D B B C B D B
二 、填空
题号 11 12 13 14 15 16 17
答案 70° 70° (4,2) 1 cm或5 cm 100 8 4﹣
解答题
18.解:∵∠A=45°,∴∠D=45°.
∵BD为⊙O的直径,∴∠BCD=90°,
∴BC=BD·sin 45°=2×=.
19.解:设⊙O的半径为r,则r=5.当PA=2 cm,
OA==<5,A在⊙O内部;
当PB=3 cm,OB==5=r,B点在⊙O上;
当PC=4 cm,OC==>5=r,点C在⊙O外
20.解:∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°,
∵OA=OD,
∴∠A=∠ADO=76°,
∴∠AOD=180°﹣∠A﹣∠ADO=180°﹣76°﹣76°=28°.
21.解:∵弓形的跨度AB=6 m,EF为弓形的高,∴OF⊥AB于点F.
∴AF=AB=3 m.
设所在⊙O的半径为r m.∵弓形的高EF=2 m,
∴OF=(r-2)m.
在Rt△AOF中,由勾股定理可知AO2=AF2+OF2,
即r2=32+(r-2)2,解得r=,
即所在⊙O的半径为 m.
22.解:(1)过点O作,垂足为E,如图
则CE=DE,AE=BE,
,
即.
(2)连接OA,OC,如图所示,
在中,,,
,
在中,,,
,
.
23.(1)证明:连接OC,如图,
∵OA=OC,∠A=30°,
∴∠ACO=∠A=30°,
∵CA=CP, ∴∠A=∠P=30°,
∴∠ACP=180°-∠A-∠P=180°-30°-30°=120°,
∴∠OCP=∠ACP-∠ACO=120°-30°=90°,
∴OC⊥CP,∴CP是⊙O的切线.
(2)解:如图,连接BC,
∵OA=OB=1,∴AB=2,
∵AB是⊙O的直径,∴∠ACB=90°,
∵∠A=30°,∴BC=AB=1,
∴AC==.
24.解:(1)连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠AOB=∠1=∠A=20°;
(2)∵∠2=∠A+∠1,
∴∠2=2∠A,
∵OB=OE,
∴∠2=∠E,
∴∠E=2∠A,
∴∠DOE=∠A+∠E=3∠A=60°.
25.解:(1)1,6
(2)如图②,当半圆O在直线AB的左侧,与直线AB相切时,
设切点为M,连接OM,则OM⊥AB,OM=6 cm.
∵∠ABC=30°,∴OB=2OM=12 cm.
又∵BC=12 cm,∴当点O与点C重合,
即点O运动到点C时,半圆O与△ABC的边AB相切,
此时点O运动了8 cm,运动时间t=8÷2=4(s).
如图③,当半圆O所在的圆在直线AB的右侧与直线AB相切时,
设切点为Q,连接OQ,则OQ⊥AB,OQ=6 cm.
在Rt△QOB中,∠OBQ=∠ABC=30°,则OB=2OQ=12 cm,
此时点O运动了12+12+8=32(cm),
运动时间t=32÷2=16(s).
综上所述,当t为4或16时,直线AB与半圆O所在的圆相切.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版九年级数学下册《圆》测试卷A
满分:120分 考试时间:90分钟
选择题。(每小题3分,共30分)
1. 已知⊙O的直径是6,点O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
2. 下列说法中正确的是( )
A.垂直于半径的直线是圆的切线 B.圆的切线垂直于半径
C.经过半径的外端的直线是圆的切线 D.圆的切线垂直于过切点的半径
3. 如图,四边形ABCD内接于☉O,AC平分∠BAD,则下列结论中正确的是 ( )
A. AB=AD B. BC=CD C.= D. ∠BCA=∠ACD
4.如果两个圆心角相等,那么( )
A.这两个圆心角所对的弦相等 B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等 D.以上说法都不对
5.如图,点A,B,C在⊙O上,∠BAC=54°,则∠BOC的度数为( )
A.27° B.108° C.116° D.128°
第3题 第5题 第6题
6.如图,AB是⊙O的直径,==,∠COD=38°,则∠AEO的度数是( )
A.52° B.57° C.66° D.78°
7.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于( )
A.20° B.30° C.40° D.50°
8.同一个圆的内接正六边形和外切正六边形的周长之比为( )
A.3∶4 B.∶2 C.2∶ D.1∶2
第7题 第9题 第10题
9.如图,PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E,交AB于点C.下列结论:①PA=PB;②AC=BC;③OC=CD;④PA·AC=PC·AO.其中正确的有( )
A.①③④ B.②③④ C.①②③ D.①②④
如图,在等边△ABC中,AB=6,点D,E分别在边BC,AC上,且BD=CE,连接AD,BE交于点F,连接CF,则CF的最小值是( )
A.3 B.2 C.4 D.3
填空题(每小题4分共28分)
11.如图,在⊙O中,=,∠A=40°,则∠B=________.
(第11题) (第12题) (第13题)
12.如图,已知△ABC的内切圆⊙O与BC边相切于点D,连接OB,OD.若∠ABC=40°,则∠BOD的度数是________.
13.如图,⊙P的半径为2,P在函数y=(x>0)的图象上运动,当⊙P与x轴相切时,点P的坐标为__________.
14. 如图,∠APB=30°,圆心在PB上的⊙O的半径为1 cm,OP=3 cm,若⊙O沿BP方向平移,当⊙O与直线PA相切时,圆心O平移的距离为____________.
第14题 第15题 第16题
15.如图,一条公路的转弯处是一段圆弧(图中的),点O是这段弧的圆心,C是上一点,OC⊥AB,垂足为D,AB=160m,CD=40m,则这段弯路的半径是 m.
16.如图,在⊙O中,AB是⊙O的直径,AB=8 cm, ==,M是 AB上一动点,CM+DM的最小值是__ __cm.
17.如图,在平面直角坐标系中,以点A(0,2)为圆心,2为半径的圆交y轴于点B.已知点C(2,0),点D为⊙A上的一动点,以CD为斜边,在CD左侧作等腰直角三角形CDE,连接BC,则△BCE面积的最小值为 .
解答题(6×3=18分)
如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,BD=2,连接CD,求BC的长.
19. 如图,过圆心O作OP⊥l,P为垂足,A,B,C为直线l上三个点,且PA=2 cm,PB=3 cm,PC=4 cm,若⊙O的半径为5 cm,OP=4 cm,判断A,B,C三点与⊙O的位置关系.
20.如图,BD=OD,∠B=38°,求∠AOD的度数.
解答题(8×3=24分)
21. 如图,某窗户由矩形和弓形组成,已知弓形的跨度AB=6 m,弓形的高EF=2 m.现计划安装玻璃,请你帮忙求出所在⊙O的半径.
22.如图,已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C和点D.
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且⊙O到直线AB的距离为6,求AC的长.
23.如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,连接AC,若CA=CP,∠A=30°.
(1)求证:CP是⊙O的切线;
(2)若OA=1,求弦AC的长.
解答题 (10×2=20分)
如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,
AE交⊙O于点B,且AB=OC.
(1)求∠AOB的度数.
(2)求∠EOD的度数.
25.( 如图,半圆O的直径DE=12 cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=12 cm.半圆O以2 cm/s的速度自左向右运动,在运动过程中,点D,E始终在直线BC上.设运动时间为t s,当t=0时,半圆O在△ABC的左侧,OC=8 cm.
(1)当t=________时,半圆O与AC所在直线第一次相切;点C到直线AB的距离为________.
(2)当t为何值时,直线AB与半圆O所在的圆相切?
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B D B B C B D B
二 、填空
题号 11 12 13 14 15 16 17
答案 70° 70° (4,2) 1 cm或5 cm 100 8 4﹣
解答题
18.解:∵∠A=45°,∴∠D=45°.
∵BD为⊙O的直径,∴∠BCD=90°,
∴BC=BD·sin 45°=2×=.
19.解:设⊙O的半径为r,则r=5.当PA=2 cm,
OA==<5,A在⊙O内部;
当PB=3 cm,OB==5=r,B点在⊙O上;
当PC=4 cm,OC==>5=r,点C在⊙O外
20.解:∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°,
∵OA=OD,
∴∠A=∠ADO=76°,
∴∠AOD=180°﹣∠A﹣∠ADO=180°﹣76°﹣76°=28°.
21.解:∵弓形的跨度AB=6 m,EF为弓形的高,∴OF⊥AB于点F.
∴AF=AB=3 m.
设所在⊙O的半径为r m.∵弓形的高EF=2 m,
∴OF=(r-2)m.
在Rt△AOF中,由勾股定理可知AO2=AF2+OF2,
即r2=32+(r-2)2,解得r=,
即所在⊙O的半径为 m.
22.解:(1)过点O作,垂足为E,如图
则CE=DE,AE=BE,
,
即.
(2)连接OA,OC,如图所示,
在中,,,
,
在中,,,
,
.
23.(1)证明:连接OC,如图,
∵OA=OC,∠A=30°,
∴∠ACO=∠A=30°,
∵CA=CP, ∴∠A=∠P=30°,
∴∠ACP=180°-∠A-∠P=180°-30°-30°=120°,
∴∠OCP=∠ACP-∠ACO=120°-30°=90°,
∴OC⊥CP,∴CP是⊙O的切线.
(2)解:如图,连接BC,
∵OA=OB=1,∴AB=2,
∵AB是⊙O的直径,∴∠ACB=90°,
∵∠A=30°,∴BC=AB=1,
∴AC==.
24.解:(1)连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠AOB=∠1=∠A=20°;
(2)∵∠2=∠A+∠1,
∴∠2=2∠A,
∵OB=OE,
∴∠2=∠E,
∴∠E=2∠A,
∴∠DOE=∠A+∠E=3∠A=60°.
25.解:(1)1,6
(2)如图②,当半圆O在直线AB的左侧,与直线AB相切时,
设切点为M,连接OM,则OM⊥AB,OM=6 cm.
∵∠ABC=30°,∴OB=2OM=12 cm.
又∵BC=12 cm,∴当点O与点C重合,
即点O运动到点C时,半圆O与△ABC的边AB相切,
此时点O运动了8 cm,运动时间t=8÷2=4(s).
如图③,当半圆O所在的圆在直线AB的右侧与直线AB相切时,
设切点为Q,连接OQ,则OQ⊥AB,OQ=6 cm.
在Rt△QOB中,∠OBQ=∠ABC=30°,则OB=2OQ=12 cm,
此时点O运动了12+12+8=32(cm),
运动时间t=32÷2=16(s).
综上所述,当t为4或16时,直线AB与半圆O所在的圆相切.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
