第六章 6.2.3 向量的数乘运算 课件(共24张PPT)
文档属性
| 名称 | 第六章 6.2.3 向量的数乘运算 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 14:20:43 | ||
图片预览





文档简介
(共24张PPT)
第六章
6.2平面向量的运算
6.2.3 向量的数乘运算
人教A版(2019)
教学目标
学习目标 数学素养
1理解向量数乘运算的概念及其几何意义. 1.数学抽象素养、运算素养.
2.掌握向量线性运算及其运算律. 2.运算素养.
3.理解两个向量共线的含义及平面向量共线定理. 3.几何直观素养.
温故知新
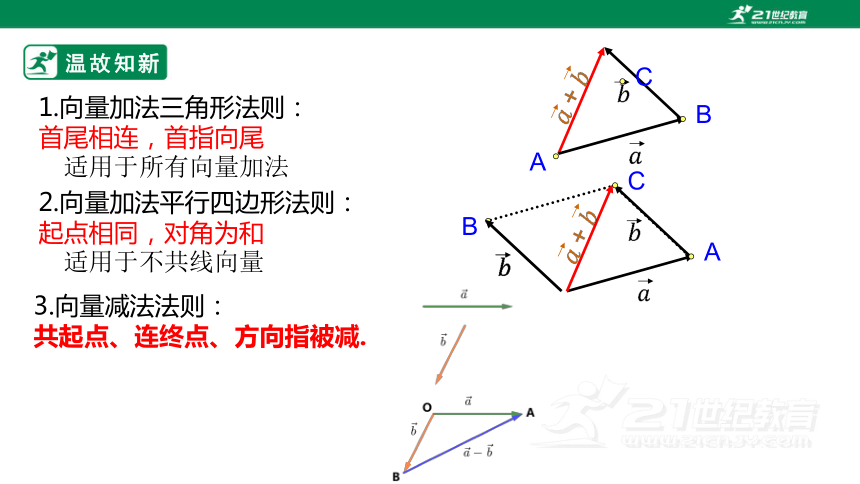
1.向量加法三角形法则:
首尾相连,首指向尾
适用于所有向量加法
A
C
B
+
2.向量加法平行四边形法则:
起点相同,对角为和
适用于不共线向量
B
A
C
+
3.向量减法法则:
共起点、连终点、方向指被减.
新知探究
1.向量的数乘
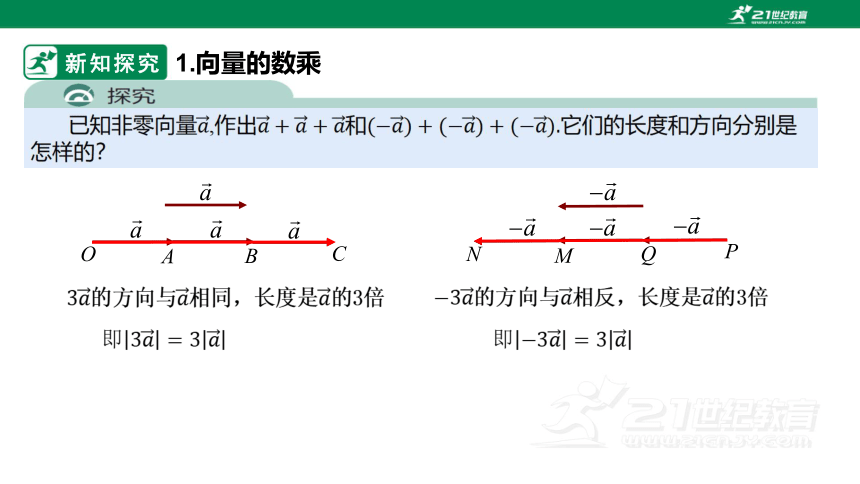
已知非零向量,作出和.它们的长度和方向分别是怎样的?
O
C
A
B
的方向与相同,长度是的3倍
即
P
Q
M
N
的方向与相反,长度是的3倍
即
新知探究
1.向量的数乘
一般地,我们规定实数λ与向量的积是一个______,这种运算叫做向量的数乘(scalar multiplication of vectors),记作λ,它的长度与方向规定如下:
⑴____________.
⑵当λ>0时,λ的方向与的方向______;
当λ<0时,λ的方向与的方向______;当λ=0时,λ=____.
向量
|λ|=|λ|||
相同
相反
由⑴⑵可知, .
问:若,则λ=0,对吗?
新知探究
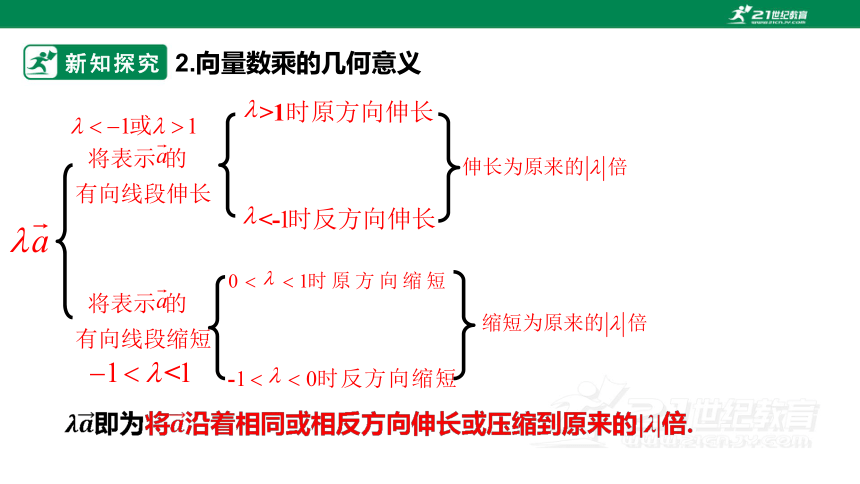
2.向量数乘的几何意义
如果把非零向量的长度伸长到原来的3.5倍,方向不变得到向量,向量该如何表示?向量之间的关系怎样?
3.5
讨论:对于非零向量,的长度与方向?
新知探究
2.向量数乘的几何意义
即为将沿着相同或相反方向伸长或压缩到原来的|λ|倍.
新知探究
3.向量数乘的运算律
数的乘法满足交换律、结合律和分配律,向量的数乘运算是否也满足上述运算律呢?
(1)根据定义,求作向量3(2)和(6)(为非零向量),并进行比较.
结合律
(2)已知向量,求作向量 (2+3)和2+3,并进行比较.
向量对实数的分配律
新知探究
3.向量数乘的运算律
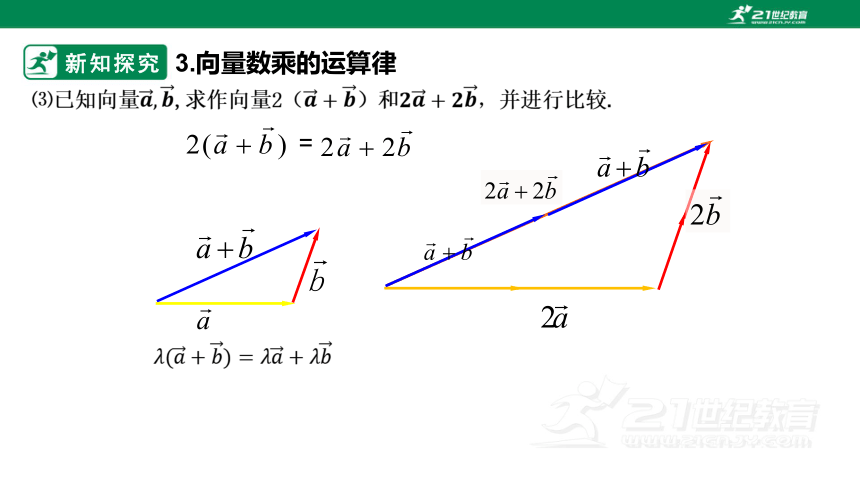
⑶已知向量,求作向量2()和,并进行比较.
=
新知探究
3.向量数乘的运算律
向量数乘的运算律:
设,是实数,那么有
(1)结合律:
(2)分配律:①
②
特别地,我们有
(-λ)=-(λ)=λ(-),
λ(-)=λ-λ.
向量的加、减、数乘运算统称为向量的线性运算.向量的线性运算的结果仍为向量.
对于任意向量,,以及任意实数λ,μ1,μ2,恒有
注意:实数与向量可以进行数乘运算,但不能进行加减运算,例如λ+,λ-是没有意义的.
新知讲解
【例1】计算:
⑴; ⑵;
⑶.
解:
⑴原式=.
⑵原式=.
⑶原式=.
注:向量与实数之间可以像多项式一样进行运算.
新知讲解
【例2】如图, ABCD的两条对角线相交于点M,且
,用表示
解:
在 ABCD中,
由平行四边形的两条对角线互相平分,得
.
A
B
C
M
D
.
.
.
.
新知探究
4.向量共线定理
引入向量数乘运算后,你能发现实数与向量的积与原向量的位置关系吗?
可以发现,实数与向量的积与原向量共线.
事实上,对于向量,如果存在实数λ,使,那么由向量数乘的定义可知与共线.
反过来,已知向量共线,且向量的长度是向量的倍,即||=,那么当与同方向时,有;当与反方向时,有.
综上,就有平面向量共线定理:
向量≠与共线的充要条件是:存在唯一一个实数,使.
数学符号表示:时,.
新知探究
4.向量共线定理
平面向量共线定理:
向量≠与共线的充要条件是:存在唯一一个实数,使.
数学符号表示:时,.
注意:定理有两层含义:①时,;②时,.
根据这一定理,设非零向量位于直线上,那么对于直线上的任意一个向量,都存在唯一的一个实数,使.
a
b
l
也就是说,位于同一直线上的向量可以由位于这条直线上的一个非零向量表示.
新知探究
【例3】如图,已知任意两个向量,试作,猜想A,B,C三点之间的位置关系,并证明你的猜想.
解:
分析:判断三点之间的位置关系,主要是看三点是否共线,为此主要看其中一点是否在另两点所确定的直线上.在本题中,判断是否存在实数,使成立.
如图,分别作向量,过点A,C作直线AC.观察发现,点B在直线AC上.猜想A,B,C三点共线.
.
.
∴.
则A,B,C三点共线.
A
B
C
O
新知探究
注意:,为什么能够判定A,B,C三点共线?
因为和有一个公共点A,同时满足时,可以判定A,B,C三点共线.
变式:若,A,B,C,D四点共线吗?
不一定,因为这两个向量没有公共点.直线AB与CD,可能平行,也可能共线!有多种情况(如下图).
A
B
C
D
A
B
C
D
新知探究
【例4】已知是两个不共线的向量,向量共线,求实数t的值.
解:
由不共线,易知向量为非零向量.
.
即.
由不共线,必有.否则,不妨设≠0,则,
由两个向量共线的充要条件知,共线,与已知矛盾.
因此,当向量共线时,.
O
由向量共线,可知存在实数,使得
由解得.
初试身手
1.= .
2.若非零向量满足,则( )
A. B. C.与方向相同 D.与方向相反
3.如图,已知P是AB的中点,试判断向量与的
关系.
1..
3..详细求解过程参照例2,构建平行四边形求解.
.
C
初试身手
4.设是不共线的两个非零向量.
⑴若,,,求证A,B,C三点共线.
⑵若共线,求实数的值
⑵解:∵与共线,∴存在实数,使得,即
.
则实数的值为.
∴A,B,C三点共线.
⑴证明:∵.
.
∵不共线,∴解得,
课堂小结
1.向量的数乘
2.向量数乘的几何意义
3.向量数乘的运算律
实数λ与向量的积是一个向量λ.
注意:实数与向量可以进行数乘运算,但不能进行加减运算,例如λ+,λ-是没有意义的.
即为将沿着相同或相反方向伸长或压缩到原来的|λ|倍.
(1)结合律:
(2)分配律:① ②
4.平面向量共线定理
向量≠与共线的充要条件是:存在唯一一个实数,使.
作业布置
作业:P22-23 习题6.2 第8⑴⑶,9,14题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第六章
6.2平面向量的运算
6.2.3 向量的数乘运算
人教A版(2019)
教学目标
学习目标 数学素养
1理解向量数乘运算的概念及其几何意义. 1.数学抽象素养、运算素养.
2.掌握向量线性运算及其运算律. 2.运算素养.
3.理解两个向量共线的含义及平面向量共线定理. 3.几何直观素养.
温故知新
1.向量加法三角形法则:
首尾相连,首指向尾
适用于所有向量加法
A
C
B
+
2.向量加法平行四边形法则:
起点相同,对角为和
适用于不共线向量
B
A
C
+
3.向量减法法则:
共起点、连终点、方向指被减.
新知探究
1.向量的数乘
已知非零向量,作出和.它们的长度和方向分别是怎样的?
O
C
A
B
的方向与相同,长度是的3倍
即
P
Q
M
N
的方向与相反,长度是的3倍
即
新知探究
1.向量的数乘
一般地,我们规定实数λ与向量的积是一个______,这种运算叫做向量的数乘(scalar multiplication of vectors),记作λ,它的长度与方向规定如下:
⑴____________.
⑵当λ>0时,λ的方向与的方向______;
当λ<0时,λ的方向与的方向______;当λ=0时,λ=____.
向量
|λ|=|λ|||
相同
相反
由⑴⑵可知, .
问:若,则λ=0,对吗?
新知探究
2.向量数乘的几何意义
如果把非零向量的长度伸长到原来的3.5倍,方向不变得到向量,向量该如何表示?向量之间的关系怎样?
3.5
讨论:对于非零向量,的长度与方向?
新知探究
2.向量数乘的几何意义
即为将沿着相同或相反方向伸长或压缩到原来的|λ|倍.
新知探究
3.向量数乘的运算律
数的乘法满足交换律、结合律和分配律,向量的数乘运算是否也满足上述运算律呢?
(1)根据定义,求作向量3(2)和(6)(为非零向量),并进行比较.
结合律
(2)已知向量,求作向量 (2+3)和2+3,并进行比较.
向量对实数的分配律
新知探究
3.向量数乘的运算律
⑶已知向量,求作向量2()和,并进行比较.
=
新知探究
3.向量数乘的运算律
向量数乘的运算律:
设,是实数,那么有
(1)结合律:
(2)分配律:①
②
特别地,我们有
(-λ)=-(λ)=λ(-),
λ(-)=λ-λ.
向量的加、减、数乘运算统称为向量的线性运算.向量的线性运算的结果仍为向量.
对于任意向量,,以及任意实数λ,μ1,μ2,恒有
注意:实数与向量可以进行数乘运算,但不能进行加减运算,例如λ+,λ-是没有意义的.
新知讲解
【例1】计算:
⑴; ⑵;
⑶.
解:
⑴原式=.
⑵原式=.
⑶原式=.
注:向量与实数之间可以像多项式一样进行运算.
新知讲解
【例2】如图, ABCD的两条对角线相交于点M,且
,用表示
解:
在 ABCD中,
由平行四边形的两条对角线互相平分,得
.
A
B
C
M
D
.
.
.
.
新知探究
4.向量共线定理
引入向量数乘运算后,你能发现实数与向量的积与原向量的位置关系吗?
可以发现,实数与向量的积与原向量共线.
事实上,对于向量,如果存在实数λ,使,那么由向量数乘的定义可知与共线.
反过来,已知向量共线,且向量的长度是向量的倍,即||=,那么当与同方向时,有;当与反方向时,有.
综上,就有平面向量共线定理:
向量≠与共线的充要条件是:存在唯一一个实数,使.
数学符号表示:时,.
新知探究
4.向量共线定理
平面向量共线定理:
向量≠与共线的充要条件是:存在唯一一个实数,使.
数学符号表示:时,.
注意:定理有两层含义:①时,;②时,.
根据这一定理,设非零向量位于直线上,那么对于直线上的任意一个向量,都存在唯一的一个实数,使.
a
b
l
也就是说,位于同一直线上的向量可以由位于这条直线上的一个非零向量表示.
新知探究
【例3】如图,已知任意两个向量,试作,猜想A,B,C三点之间的位置关系,并证明你的猜想.
解:
分析:判断三点之间的位置关系,主要是看三点是否共线,为此主要看其中一点是否在另两点所确定的直线上.在本题中,判断是否存在实数,使成立.
如图,分别作向量,过点A,C作直线AC.观察发现,点B在直线AC上.猜想A,B,C三点共线.
.
.
∴.
则A,B,C三点共线.
A
B
C
O
新知探究
注意:,为什么能够判定A,B,C三点共线?
因为和有一个公共点A,同时满足时,可以判定A,B,C三点共线.
变式:若,A,B,C,D四点共线吗?
不一定,因为这两个向量没有公共点.直线AB与CD,可能平行,也可能共线!有多种情况(如下图).
A
B
C
D
A
B
C
D
新知探究
【例4】已知是两个不共线的向量,向量共线,求实数t的值.
解:
由不共线,易知向量为非零向量.
.
即.
由不共线,必有.否则,不妨设≠0,则,
由两个向量共线的充要条件知,共线,与已知矛盾.
因此,当向量共线时,.
O
由向量共线,可知存在实数,使得
由解得.
初试身手
1.= .
2.若非零向量满足,则( )
A. B. C.与方向相同 D.与方向相反
3.如图,已知P是AB的中点,试判断向量与的
关系.
1..
3..详细求解过程参照例2,构建平行四边形求解.
.
C
初试身手
4.设是不共线的两个非零向量.
⑴若,,,求证A,B,C三点共线.
⑵若共线,求实数的值
⑵解:∵与共线,∴存在实数,使得,即
.
则实数的值为.
∴A,B,C三点共线.
⑴证明:∵.
.
∵不共线,∴解得,
课堂小结
1.向量的数乘
2.向量数乘的几何意义
3.向量数乘的运算律
实数λ与向量的积是一个向量λ.
注意:实数与向量可以进行数乘运算,但不能进行加减运算,例如λ+,λ-是没有意义的.
即为将沿着相同或相反方向伸长或压缩到原来的|λ|倍.
(1)结合律:
(2)分配律:① ②
4.平面向量共线定理
向量≠与共线的充要条件是:存在唯一一个实数,使.
作业布置
作业:P22-23 习题6.2 第8⑴⑶,9,14题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
