九年级数学23.1.1 图形的旋转 说课课件(共27张PPT)
文档属性
| 名称 | 九年级数学23.1.1 图形的旋转 说课课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 14:06:54 | ||
图片预览




文档简介
(共27张PPT)
23.1.1图形的旋转
说目标
本节课是人教版《数学》九年级上册第23章“23.1图形的旋转”的第一课时,是一节概念课,在此之前,学生已经学习了轴对称、平移两种图形变换,对图形变换已具有一定的认识,旋转是在此基础上发展学生空间观念的一个渗透,是后续学习中心对称图形及其图形变化的基础,是空间与图形领域的基础知识,在教材中,起着承上启下的作用。通过本节课的学习,学生对图形的变换会更完整,同时,旋转在日常生活中的应用也非常广泛,利用旋转可以帮助我们解决很多实际问题。
说教法学法
说教学程序
说评价
说教材
所处地位作用及前后联系
说目标
说教法学法
说教学程序
说教学设计
说教材
探索旋转的基本性质
教学 重点
旋转的基本要素与基本性质
教学 难点
说教法学法
说教学程序
说教学设计
说教材
知识技能目标:通过具体实例认识旋转,理解旋转的基本含义,探索旋转的基本性质。
能力目标:让学生经历观察、分析、操作、交流的过程,培养学生的说理能力;了解观察探究的基本方法,学会解决问题的基本策略,增强应用数学的意识。
情感目标:体验和感受数学活动的探究性,拉近数学与生活的距离,从而进一步培养学生的合作意识和审美情趣。
说目标
教学
目标
说教学程序
说教学设计
说教材
说目标
1.遵循学生是学习的主人的原则,在为学生创造大量实例的基础上,引导学生自主思考、交流、讨论、类比、归纳、学习。
2.借用多媒体课件与实物辅助教学,力求使每个学生都能在原有的基础上得到发展,既满足了学生对新知识的强烈探索欲望,又排除学生学习几何方法的缺乏,和学无所用的顾虑,让他们在学习过程中获得愉快与进步。
说教法学法
说 教 法
说教学程序
说教学设计
说教材
说目标
1、探究研讨法
2、比较学习法
说教法学法
说 学 法
说教学设计
说教材
说目标
说教学方法
说教学程序
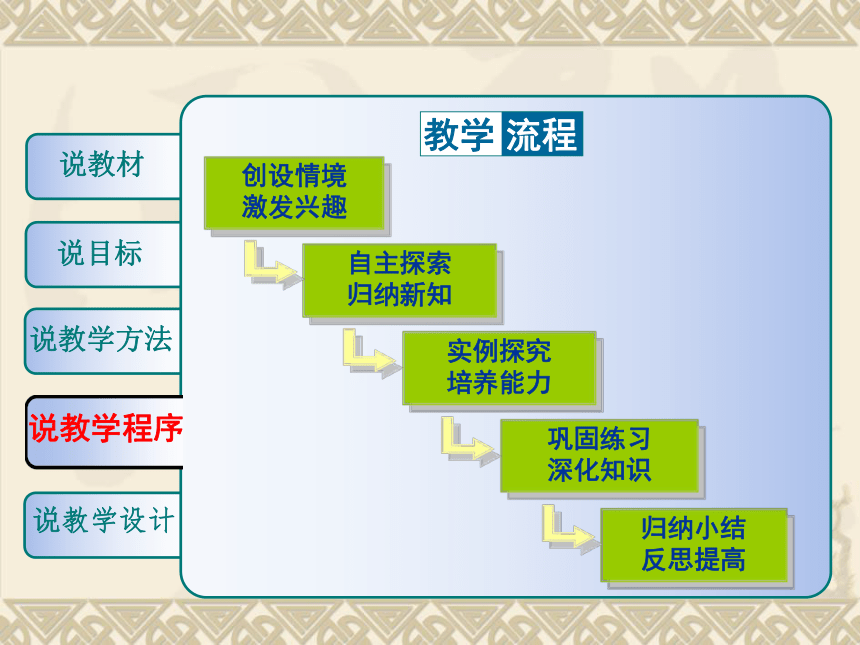
创设情境
激发兴趣
自主探索
归纳新知
实例探究
培养能力
归纳小结
反思提高
巩固练习
深化知识
教学 流程
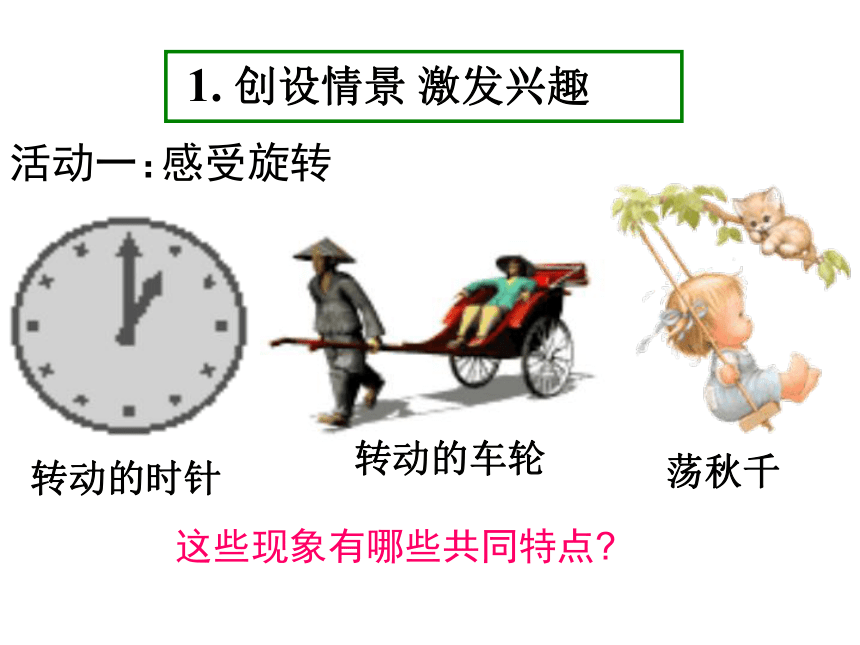
活动一:
感受旋转
1. 创设情景 激发兴趣
这些现象有哪些共同特点
荡秋千
转动的车轮
转动的时针
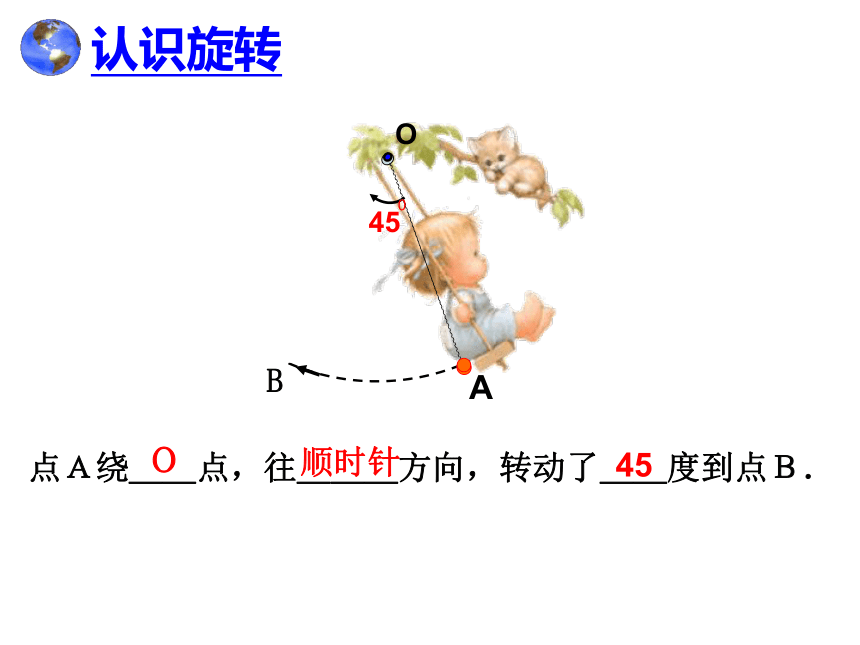
B
O
A
45
0
点A绕__点,往___方向,转动了__度到点B.
O
顺时针
45
认识旋转
认识旋转
O
B
A
B
/
A
/
60
0
35
0
B
A
B
A
C
C
O
100
0
认识旋转
O
B
A
B
/
A
/
B
A
B
A
C
C
O
在平面内,把一个图形绕着某一个定点转动一个角度的图形变换叫作旋转(Circumrotation).
B
O
A
认识旋转
这个定点称为旋转中心,
旋转的概念
旋转中心,
所转动的角称为旋转角.
这些运动有什么共同特点
如果图形上的点A经过旋转变为A’,
那么这两点叫做这个旋转的对应点.
旋转角度,
旋转方向.
旋转的三要素:
找一找
A
B
O
C
D
点A的对应点是________;
旋转中心是________;
旋转角是_________________;
(1)如图,△ABO绕点O旋转得到△CDO,则:
点C
点O
∠AOC,
∠BOD
B
A
E
D
C
F
O
试一试
如图,△ABC绕点O旋转得到△ DEF,则:
点C的对应点是________;
旋转中心是________;
旋转角是_________________ ;
点F
点O
∠AOD,
∠BOE,
∠COF
旋转有什么性质
2.自主探索 归纳新知
B/
A/
A
B
C/
C
O
探究的问题:
旋转前、后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
旋转的性质:
1.在图形的旋转过程中,哪些发生了改变 哪些没有发
生改变
2.分别连结对应点A、A/与旋转中心O,量一量线段OA与
线段OA/,它们有什么关系 任意找一对对应点,量一下
对应点到旋转中心的距离,你能发现什么规律
3.量一下∠AOA/的度数,再任意找几对对应点,分别 量一下对应点与旋转中心所连线段的夹角的度数,你又能发现什么规律?
活动二:探究性质
香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?
3.实例探究 培养能力
活动三:
知识应用
如图: ABC是等边三角形,D是BC
上一点, ABD经过旋转后到达 ACE的
位置。(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置?
E
D
C
B
A
M
.
例 题
点A
60度
N .
AC中点N
下列现象中属于旋转的有( ) 个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
随堂练习1
4.巩固练习 深化知识
C
如图:P是等边 ABC内的一点,把 ABP按不同的方向通过旋转得到 BQC和 ACR,
(1)指出旋转中心、旋转方向和旋转角度?
(2) ACR是否可以直接通过把 BQC旋转得到?
A
Q
R
P
C
B
随堂练习2
已知,如图边长为1的正方形EFOG绕与之边长相等的正方形ABCD的对角线交点O旋转任意角度,求图中重叠部分的面积.
0.25
M
H
随堂练习3
已知,如图边长为1的正方形EFOG绕与之边长相等的正方形ABCD的对角线交点O旋转任意角度,求图中重叠部分的面积.
0.25
H/
H
M/
M
随堂练习3
◆什么叫图形的旋转
◆图形旋转的性质是什么
在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形运动叫做图形的旋转.这个定点叫旋转中心.旋转的角度称为旋转角.
1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
5.归纳小结 反思提高
平移变换
A
B
C
A/
C/
B/
◆对比平移这种图形变换,旋转变换与
它有哪些共性和区别
(1)著名汽车标志
(2)商标
(3)国旗、区旗
请设计一个绕一点旋转600后能与自身重合的图形.
动手操作
说教材
说目标
说教法学法
说教学程序
本节课的教学以观察、分析现实生活中的实例为切入点,以探究活动为主线设计了一系列的数学活动.让学生通过贴近生活的例子认识旋转,通过动手进行数学实验探索旋转的基本性质,通过解决实际问题、数学问题掌握旋转的性质,激活了学生的思维,激发了学习的兴趣,增强了学生应用数学的意识 。
说教学设计
教学 设计
23.1.1图形的旋转
说目标
本节课是人教版《数学》九年级上册第23章“23.1图形的旋转”的第一课时,是一节概念课,在此之前,学生已经学习了轴对称、平移两种图形变换,对图形变换已具有一定的认识,旋转是在此基础上发展学生空间观念的一个渗透,是后续学习中心对称图形及其图形变化的基础,是空间与图形领域的基础知识,在教材中,起着承上启下的作用。通过本节课的学习,学生对图形的变换会更完整,同时,旋转在日常生活中的应用也非常广泛,利用旋转可以帮助我们解决很多实际问题。
说教法学法
说教学程序
说评价
说教材
所处地位作用及前后联系
说目标
说教法学法
说教学程序
说教学设计
说教材
探索旋转的基本性质
教学 重点
旋转的基本要素与基本性质
教学 难点
说教法学法
说教学程序
说教学设计
说教材
知识技能目标:通过具体实例认识旋转,理解旋转的基本含义,探索旋转的基本性质。
能力目标:让学生经历观察、分析、操作、交流的过程,培养学生的说理能力;了解观察探究的基本方法,学会解决问题的基本策略,增强应用数学的意识。
情感目标:体验和感受数学活动的探究性,拉近数学与生活的距离,从而进一步培养学生的合作意识和审美情趣。
说目标
教学
目标
说教学程序
说教学设计
说教材
说目标
1.遵循学生是学习的主人的原则,在为学生创造大量实例的基础上,引导学生自主思考、交流、讨论、类比、归纳、学习。
2.借用多媒体课件与实物辅助教学,力求使每个学生都能在原有的基础上得到发展,既满足了学生对新知识的强烈探索欲望,又排除学生学习几何方法的缺乏,和学无所用的顾虑,让他们在学习过程中获得愉快与进步。
说教法学法
说 教 法
说教学程序
说教学设计
说教材
说目标
1、探究研讨法
2、比较学习法
说教法学法
说 学 法
说教学设计
说教材
说目标
说教学方法
说教学程序
创设情境
激发兴趣
自主探索
归纳新知
实例探究
培养能力
归纳小结
反思提高
巩固练习
深化知识
教学 流程
活动一:
感受旋转
1. 创设情景 激发兴趣
这些现象有哪些共同特点
荡秋千
转动的车轮
转动的时针
B
O
A
45
0
点A绕__点,往___方向,转动了__度到点B.
O
顺时针
45
认识旋转
认识旋转
O
B
A
B
/
A
/
60
0
35
0
B
A
B
A
C
C
O
100
0
认识旋转
O
B
A
B
/
A
/
B
A
B
A
C
C
O
在平面内,把一个图形绕着某一个定点转动一个角度的图形变换叫作旋转(Circumrotation).
B
O
A
认识旋转
这个定点称为旋转中心,
旋转的概念
旋转中心,
所转动的角称为旋转角.
这些运动有什么共同特点
如果图形上的点A经过旋转变为A’,
那么这两点叫做这个旋转的对应点.
旋转角度,
旋转方向.
旋转的三要素:
找一找
A
B
O
C
D
点A的对应点是________;
旋转中心是________;
旋转角是_________________;
(1)如图,△ABO绕点O旋转得到△CDO,则:
点C
点O
∠AOC,
∠BOD
B
A
E
D
C
F
O
试一试
如图,△ABC绕点O旋转得到△ DEF,则:
点C的对应点是________;
旋转中心是________;
旋转角是_________________ ;
点F
点O
∠AOD,
∠BOE,
∠COF
旋转有什么性质
2.自主探索 归纳新知
B/
A/
A
B
C/
C
O
探究的问题:
旋转前、后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
旋转的性质:
1.在图形的旋转过程中,哪些发生了改变 哪些没有发
生改变
2.分别连结对应点A、A/与旋转中心O,量一量线段OA与
线段OA/,它们有什么关系 任意找一对对应点,量一下
对应点到旋转中心的距离,你能发现什么规律
3.量一下∠AOA/的度数,再任意找几对对应点,分别 量一下对应点与旋转中心所连线段的夹角的度数,你又能发现什么规律?
活动二:探究性质
香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?
3.实例探究 培养能力
活动三:
知识应用
如图: ABC是等边三角形,D是BC
上一点, ABD经过旋转后到达 ACE的
位置。(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置?
E
D
C
B
A
M
.
例 题
点A
60度
N .
AC中点N
下列现象中属于旋转的有( ) 个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
随堂练习1
4.巩固练习 深化知识
C
如图:P是等边 ABC内的一点,把 ABP按不同的方向通过旋转得到 BQC和 ACR,
(1)指出旋转中心、旋转方向和旋转角度?
(2) ACR是否可以直接通过把 BQC旋转得到?
A
Q
R
P
C
B
随堂练习2
已知,如图边长为1的正方形EFOG绕与之边长相等的正方形ABCD的对角线交点O旋转任意角度,求图中重叠部分的面积.
0.25
M
H
随堂练习3
已知,如图边长为1的正方形EFOG绕与之边长相等的正方形ABCD的对角线交点O旋转任意角度,求图中重叠部分的面积.
0.25
H/
H
M/
M
随堂练习3
◆什么叫图形的旋转
◆图形旋转的性质是什么
在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形运动叫做图形的旋转.这个定点叫旋转中心.旋转的角度称为旋转角.
1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
5.归纳小结 反思提高
平移变换
A
B
C
A/
C/
B/
◆对比平移这种图形变换,旋转变换与
它有哪些共性和区别
(1)著名汽车标志
(2)商标
(3)国旗、区旗
请设计一个绕一点旋转600后能与自身重合的图形.
动手操作
说教材
说目标
说教法学法
说教学程序
本节课的教学以观察、分析现实生活中的实例为切入点,以探究活动为主线设计了一系列的数学活动.让学生通过贴近生活的例子认识旋转,通过动手进行数学实验探索旋转的基本性质,通过解决实际问题、数学问题掌握旋转的性质,激活了学生的思维,激发了学习的兴趣,增强了学生应用数学的意识 。
说教学设计
教学 设计
同课章节目录
