九年级数学23.1.1 图形的旋转 说课课件(共18张PPT)
文档属性
| 名称 | 九年级数学23.1.1 图形的旋转 说课课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
23.1图形的旋转
新人教版九年级上《旋转》
说 课 内 容
教学背景分析
教学目标分析
教学重难点分析
教法与学法分析
教学过程分析
一、教学背景分析
1、教材分析
本课是人教版九年级数学上册第二十三章《旋转》第一节的内容。是继图形的平移、轴对称之后的又一种基本图形变换,是新课标体系教材中图形变换的一个重要组成部分。并且“图形的旋转”本身就是一种重要的数学变换思想,它不仅为本章后续学习“中心对称”打下基础,更为后面章节“圆”的相关学习做了铺垫。因此本节课的学习在教材中具有重要的作用。
2、学情分析
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
2、学生在七、八年级相继学习平移、轴对称两种基本变换,具有一定的观察、分析、抽象、概括的经验和能力。但是我们都知道九年级的学生思维方式仍以直观形象思维为主,抽象逻辑思维能力,分析概括能力相对薄弱。这些方面需要老师适时的引导和点拨。
二、教学目标分析
知识与技能:理解图形旋转的概念与性质。
过程与方法:经历图形旋转概念的形成过程和性质的探索过程,发展直观想象能力,逐步提高分析、归纳、抽象概括的思维能力。
情感态度、价值观:在实际探索过程中感知数学的美,体会数学广泛的实际应用,从而培养学习数学的浓厚兴趣。
三、教学重难点分析
教学重点:
归纳图形旋转的有关概念及性质。
教学难点:
概念的形成过程和性质的探索过程。
我相信这样既能突出重点、突破难点教学,也会极大的激发学生的学习兴趣。
并且“图形的旋转”本身就是一种重要的数学变换思想,它不仅为本章后续学习“中心对称”打下基础,更为后面章节“圆”的相关学习做了铺垫。
1、问题情境,导入新课
△ ABC ≌△A′B′C′
在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
OA与OA ′相等吗?OB与OB ′相等吗?
设计意图:既内化定义,加深对应点和旋转角的理解,又为后面的探究埋下伏笔。
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
∠ABE′=∠ADE=90°, BE′=DE .
说一说:旋转的基本性质
过程与方法:经历图形旋转概念的形成过程和性质的探索过程,发展直观想象能力,逐步提高分析、归纳、抽象概括的思维能力。
新人教版九年级上《旋转》
2、自主探索,归纳新知
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
将例题中的“顺时针”改为“逆时针”,请完 成作图。
∠AOA ′ =∠BOB ′=∠COC ′
说一说:旋转的基本性质
△ ABC ≌△A′B′C′
解:因为点A是旋转中心,所以它的对应点是它本身.
举出一些生活中的实例,并指出旋转中心和旋转角.
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
四、教法学法分析
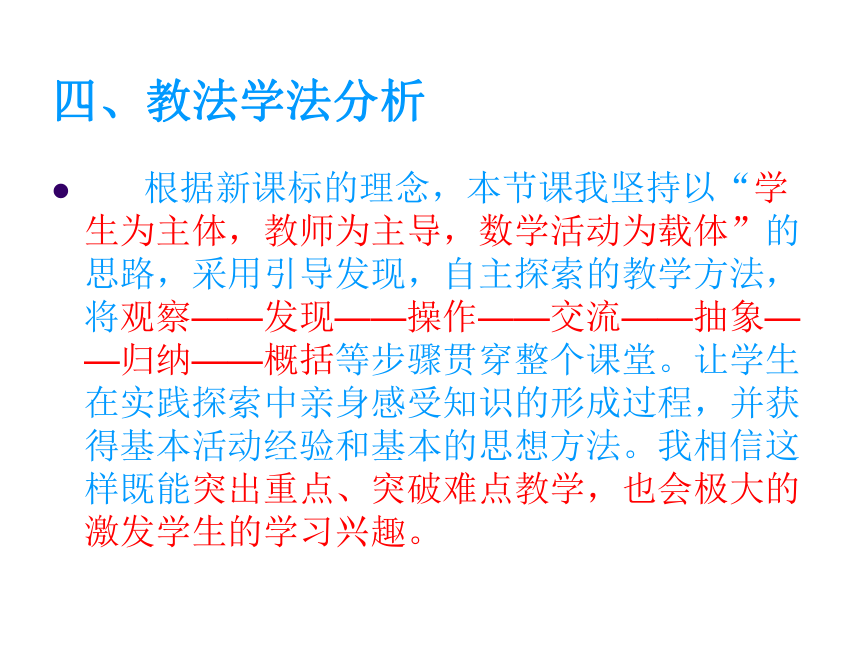
根据新课标的理念,本节课我坚持以“学生为主体,教师为主导,数学活动为载体”的思路,采用引导发现,自主探索的教学方法,将观察——发现——操作——交流——抽象——归纳——概括等步骤贯穿整个课堂。让学生在实践探索中亲身感受知识的形成过程,并获得基本活动经验和基本的思想方法。我相信这样既能突出重点、突破难点教学,也会极大的激发学生的学习兴趣。
五、教学过程分析
问题情境,导入新课
自主探索,归纳新知
巩固新知,形成技能
小结作业,深化提高
1、问题情境,导入新课
观察实例,回答问题
上面情景中的转动现象,有什么共同的特征?
把一个平面图形绕着平面内某一点O转动一个角度,就叫做图形的旋转。点0叫做旋转中心。转动的角叫做旋转角。
如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的对应点
举出一些生活中的实例,并指出旋转中心和旋转角.
2、自主探索,归纳新知
想一想:如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
OA与OA ′相等吗?OB与OB ′相等吗?
∠AOA ′ 与∠BOB ′相等吗
旋转过程中杠杆的长度发生变化了吗?
设计意图:既内化定义,加深对应点和旋转角的理解,又为后面的探究埋下伏笔。
做一做:请大家在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形洞( △A′B′C′ ),然后围绕O转动硬纸板,再描出这个挖掉的三角形洞(△ ABC ),移开硬纸板.
请大家运用刻度尺和量角器度量线段和有关 角,并探索旋转的性质.
A
B
C
A′
B′
C′
O
OA=OA ′ OB=OB ′
∠AOA ′ =∠BOB ′=∠COC ′
△ ABC ≌△A′B′C′
说一说:旋转的基本性质
1.对应点到旋转中心的距离相等
2对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等
(旋转不改变图形的大小和形状)
设计意图:通过学生自己亲自动手操作,测量,发现,交流,归纳最后得出结论。突出了重点,突破了难点,同时激发起了学生的学习兴趣,也提高了学生动手实践能力和归纳概括能力。
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
三、巩固新知,形成技能
引导分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以
∠ABE′=∠ADE=90°, BE′=DE .
解:因为点A是旋转中心,所以它的对应点是它本身.
在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
因此,在CB的延长线上取点E′ ,使BE′ =DE,则△ABE′为旋转后的图形.
解一解
你还有其他方法吗?鼓励学生用多种方法解决问题,要求学生说出每种作图方法的理论依据。逐步提高学生发散思维能力和数学语言表达能力。
在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
∠ABE′=∠ADE=90°, BE′=DE .
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
将例题中的“顺时针”改为“逆时针”,请完 成作图。
∠ABE′=∠ADE=90°, BE′=DE .
将例题中的“顺时针”改为“逆时针”,请完 成作图。
想一想:如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
举出一些生活中的实例,并指出旋转中心和旋转角.
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以
2、学生在七、八年级相继学习平移、轴对称两种基本变换,具有一定的观察、分析、抽象、概括的经验和能力。
突出了重点,突破了难点,同时激发起了学生的学习兴趣,也提高了学生动手实践能力和归纳概括能力。
2、自主探索,归纳新知
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
逐步提高学生发散思维能力和数学语言表达能力。
如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的对应点
找出图中扳手拧螺母时的旋转中心和旋转角.
引导分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
并且“图形的旋转”本身就是一种重要的数学变换思想,它不仅为本章后续学习“中心对称”打下基础,更为后面章节“圆”的相关学习做了铺垫。
说 课 内 容
解:因为点A是旋转中心,所以它的对应点是它本身.
因此,在CB的延长线上取点E′ ,使BE′ =DE,则△ABE′为旋转后的图形.
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
∠AOA ′ 与∠BOB ′相等吗
练习1.如图,小明坐在秋千上,秋千旋转了80°.请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点.
A
B
M
N
练习2.如图,用左面的三角形经过怎样旋转,可以得到右面的图形.
练习3.找出图中扳手拧螺母时的旋转中心和旋转角.
O
A
B
四、小结作业、深化提高
今天这节课我们学习了那些内容,你学会了那些思想方法,在学习的过程中有什么感受?请同学们畅所欲言!
课堂小结:
分层作业
1.将例题中的“顺时针”改为“逆时针”,请完 成作图。
2习题23.1第4题
3把一个三角形进行旋转:选择不同的旋转中心、不同的旋转角,看看旋转的效果有什么不同。
23.1图形的旋转
新人教版九年级上《旋转》
说 课 内 容
教学背景分析
教学目标分析
教学重难点分析
教法与学法分析
教学过程分析
一、教学背景分析
1、教材分析
本课是人教版九年级数学上册第二十三章《旋转》第一节的内容。是继图形的平移、轴对称之后的又一种基本图形变换,是新课标体系教材中图形变换的一个重要组成部分。并且“图形的旋转”本身就是一种重要的数学变换思想,它不仅为本章后续学习“中心对称”打下基础,更为后面章节“圆”的相关学习做了铺垫。因此本节课的学习在教材中具有重要的作用。
2、学情分析
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
2、学生在七、八年级相继学习平移、轴对称两种基本变换,具有一定的观察、分析、抽象、概括的经验和能力。但是我们都知道九年级的学生思维方式仍以直观形象思维为主,抽象逻辑思维能力,分析概括能力相对薄弱。这些方面需要老师适时的引导和点拨。
二、教学目标分析
知识与技能:理解图形旋转的概念与性质。
过程与方法:经历图形旋转概念的形成过程和性质的探索过程,发展直观想象能力,逐步提高分析、归纳、抽象概括的思维能力。
情感态度、价值观:在实际探索过程中感知数学的美,体会数学广泛的实际应用,从而培养学习数学的浓厚兴趣。
三、教学重难点分析
教学重点:
归纳图形旋转的有关概念及性质。
教学难点:
概念的形成过程和性质的探索过程。
我相信这样既能突出重点、突破难点教学,也会极大的激发学生的学习兴趣。
并且“图形的旋转”本身就是一种重要的数学变换思想,它不仅为本章后续学习“中心对称”打下基础,更为后面章节“圆”的相关学习做了铺垫。
1、问题情境,导入新课
△ ABC ≌△A′B′C′
在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
OA与OA ′相等吗?OB与OB ′相等吗?
设计意图:既内化定义,加深对应点和旋转角的理解,又为后面的探究埋下伏笔。
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
∠ABE′=∠ADE=90°, BE′=DE .
说一说:旋转的基本性质
过程与方法:经历图形旋转概念的形成过程和性质的探索过程,发展直观想象能力,逐步提高分析、归纳、抽象概括的思维能力。
新人教版九年级上《旋转》
2、自主探索,归纳新知
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
将例题中的“顺时针”改为“逆时针”,请完 成作图。
∠AOA ′ =∠BOB ′=∠COC ′
说一说:旋转的基本性质
△ ABC ≌△A′B′C′
解:因为点A是旋转中心,所以它的对应点是它本身.
举出一些生活中的实例,并指出旋转中心和旋转角.
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
四、教法学法分析
根据新课标的理念,本节课我坚持以“学生为主体,教师为主导,数学活动为载体”的思路,采用引导发现,自主探索的教学方法,将观察——发现——操作——交流——抽象——归纳——概括等步骤贯穿整个课堂。让学生在实践探索中亲身感受知识的形成过程,并获得基本活动经验和基本的思想方法。我相信这样既能突出重点、突破难点教学,也会极大的激发学生的学习兴趣。
五、教学过程分析
问题情境,导入新课
自主探索,归纳新知
巩固新知,形成技能
小结作业,深化提高
1、问题情境,导入新课
观察实例,回答问题
上面情景中的转动现象,有什么共同的特征?
把一个平面图形绕着平面内某一点O转动一个角度,就叫做图形的旋转。点0叫做旋转中心。转动的角叫做旋转角。
如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的对应点
举出一些生活中的实例,并指出旋转中心和旋转角.
2、自主探索,归纳新知
想一想:如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
OA与OA ′相等吗?OB与OB ′相等吗?
∠AOA ′ 与∠BOB ′相等吗
旋转过程中杠杆的长度发生变化了吗?
设计意图:既内化定义,加深对应点和旋转角的理解,又为后面的探究埋下伏笔。
做一做:请大家在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形洞( △A′B′C′ ),然后围绕O转动硬纸板,再描出这个挖掉的三角形洞(△ ABC ),移开硬纸板.
请大家运用刻度尺和量角器度量线段和有关 角,并探索旋转的性质.
A
B
C
A′
B′
C′
O
OA=OA ′ OB=OB ′
∠AOA ′ =∠BOB ′=∠COC ′
△ ABC ≌△A′B′C′
说一说:旋转的基本性质
1.对应点到旋转中心的距离相等
2对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等
(旋转不改变图形的大小和形状)
设计意图:通过学生自己亲自动手操作,测量,发现,交流,归纳最后得出结论。突出了重点,突破了难点,同时激发起了学生的学习兴趣,也提高了学生动手实践能力和归纳概括能力。
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
三、巩固新知,形成技能
引导分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以
∠ABE′=∠ADE=90°, BE′=DE .
解:因为点A是旋转中心,所以它的对应点是它本身.
在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
因此,在CB的延长线上取点E′ ,使BE′ =DE,则△ABE′为旋转后的图形.
解一解
你还有其他方法吗?鼓励学生用多种方法解决问题,要求学生说出每种作图方法的理论依据。逐步提高学生发散思维能力和数学语言表达能力。
在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
∠ABE′=∠ADE=90°, BE′=DE .
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
将例题中的“顺时针”改为“逆时针”,请完 成作图。
∠ABE′=∠ADE=90°, BE′=DE .
将例题中的“顺时针”改为“逆时针”,请完 成作图。
想一想:如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
举出一些生活中的实例,并指出旋转中心和旋转角.
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以
2、学生在七、八年级相继学习平移、轴对称两种基本变换,具有一定的观察、分析、抽象、概括的经验和能力。
突出了重点,突破了难点,同时激发起了学生的学习兴趣,也提高了学生动手实践能力和归纳概括能力。
2、自主探索,归纳新知
1、学生小学就进行过相关概念的学习,并且结合实际生活中的常见物品有一定的直观感受。
逐步提高学生发散思维能力和数学语言表达能力。
如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的对应点
找出图中扳手拧螺母时的旋转中心和旋转角.
引导分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
并且“图形的旋转”本身就是一种重要的数学变换思想,它不仅为本章后续学习“中心对称”打下基础,更为后面章节“圆”的相关学习做了铺垫。
说 课 内 容
解:因为点A是旋转中心,所以它的对应点是它本身.
因此,在CB的延长线上取点E′ ,使BE′ =DE,则△ABE′为旋转后的图形.
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
∠AOA ′ 与∠BOB ′相等吗
练习1.如图,小明坐在秋千上,秋千旋转了80°.请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点.
A
B
M
N
练习2.如图,用左面的三角形经过怎样旋转,可以得到右面的图形.
练习3.找出图中扳手拧螺母时的旋转中心和旋转角.
O
A
B
四、小结作业、深化提高
今天这节课我们学习了那些内容,你学会了那些思想方法,在学习的过程中有什么感受?请同学们畅所欲言!
课堂小结:
分层作业
1.将例题中的“顺时针”改为“逆时针”,请完 成作图。
2习题23.1第4题
3把一个三角形进行旋转:选择不同的旋转中心、不同的旋转角,看看旋转的效果有什么不同。
同课章节目录
