2024年中考数学复习专项练习题:二次函数(含答案)
文档属性
| 名称 | 2024年中考数学复习专项练习题:二次函数(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 198.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 00:00:00 | ||
图片预览


文档简介
2024年中考数学复习专项练习题:二次函数
一、选择题
1.下列函数中属于二次函数的是( )
A. B.
C. D.
2.把抛物线向右平移3个单位,再向下平移2个单位,得到抛物线( )
A. B.
C. D.
3.关于的图象,下列叙述正确的是( )
A.顶点坐标为 B.对称轴为直线
C.当时,随的增大而增大 D.开口向下
4.若抛物线经过点,则该抛物线一定还经过点( )
A. B. C. D.
5.已知二次函数的图象经过点和.若,则的取值范围是( )
A. B.
C.或 D.
6.已知y=ax+b的图象如图所示,则y=ax2+bx的图象有可能是( )
A. B. C. D.
7.已知,抛物线与一个交点为.规定:当时,;当时,;下列结论:①有最小值3;②关于函数图象关于直线对称;③直线与关于的函数图象有4个交点;④当时,随的增大而减小.其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
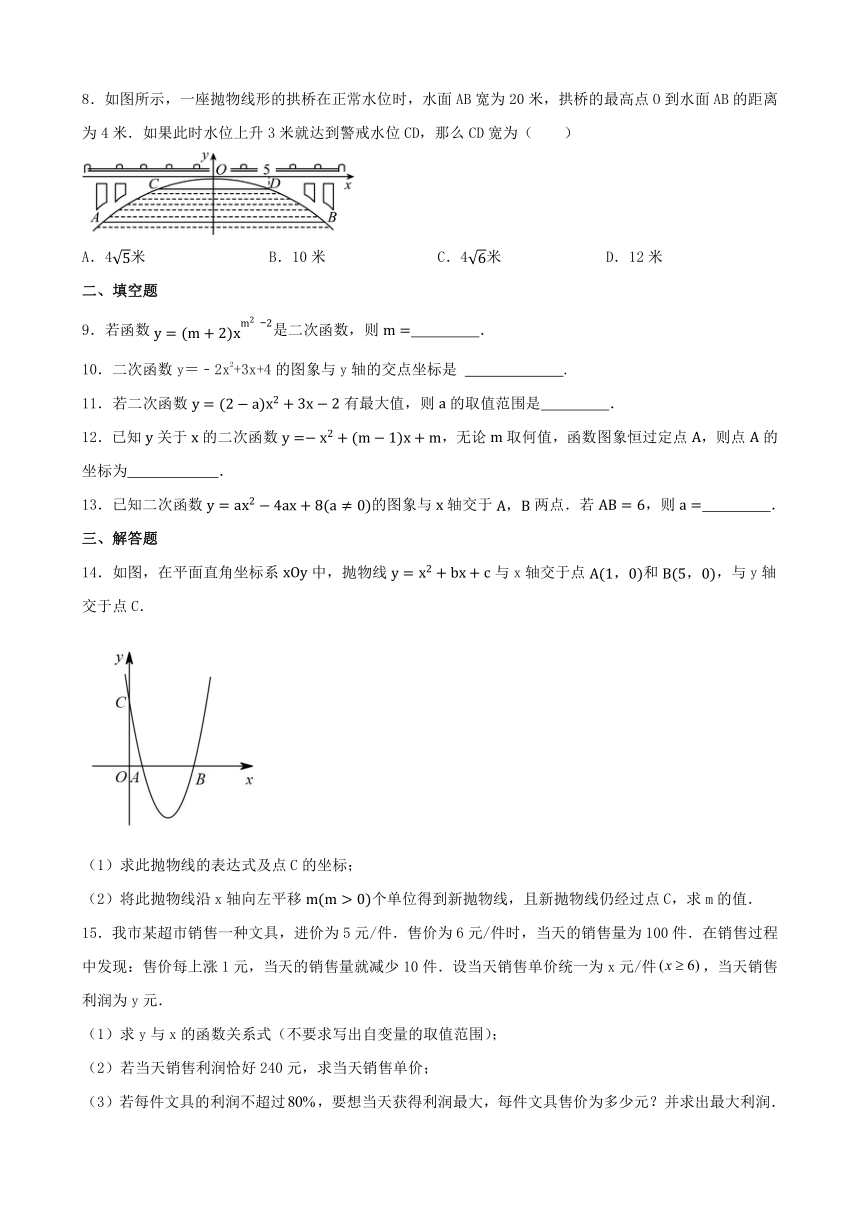
8.如图所示,一座抛物线形的拱桥在正常水位时,水面AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD,那么CD宽为( )
A.4米 B.10米 C.4米 D.12米
二、填空题
9.若函数是二次函数,则 .
10.二次函数y=﹣2x2+3x+4的图象与y轴的交点坐标是 .
11.若二次函数有最大值,则的取值范围是 .
12.已知关于的二次函数,无论取何值,函数图象恒过定点,则点的坐标为 .
13.已知二次函数的图象与轴交于两点.若,则 .
三、解答题
14.如图,在平面直角坐标系中,抛物线与x轴交于点和,与y轴交于点C.
(1)求此抛物线的表达式及点C的坐标;
(2)将此抛物线沿x轴向左平移个单位得到新抛物线,且新抛物线仍经过点C,求m的值.
15.我市某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨1元,当天的销售量就减少10件.设当天销售单价统一为x元/件,当天销售利润为y元.
(1)求y与x的函数关系式(不要求写出自变量的取值范围);
(2)若当天销售利润恰好240元,求当天销售单价;
(3)若每件文具的利润不超过,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
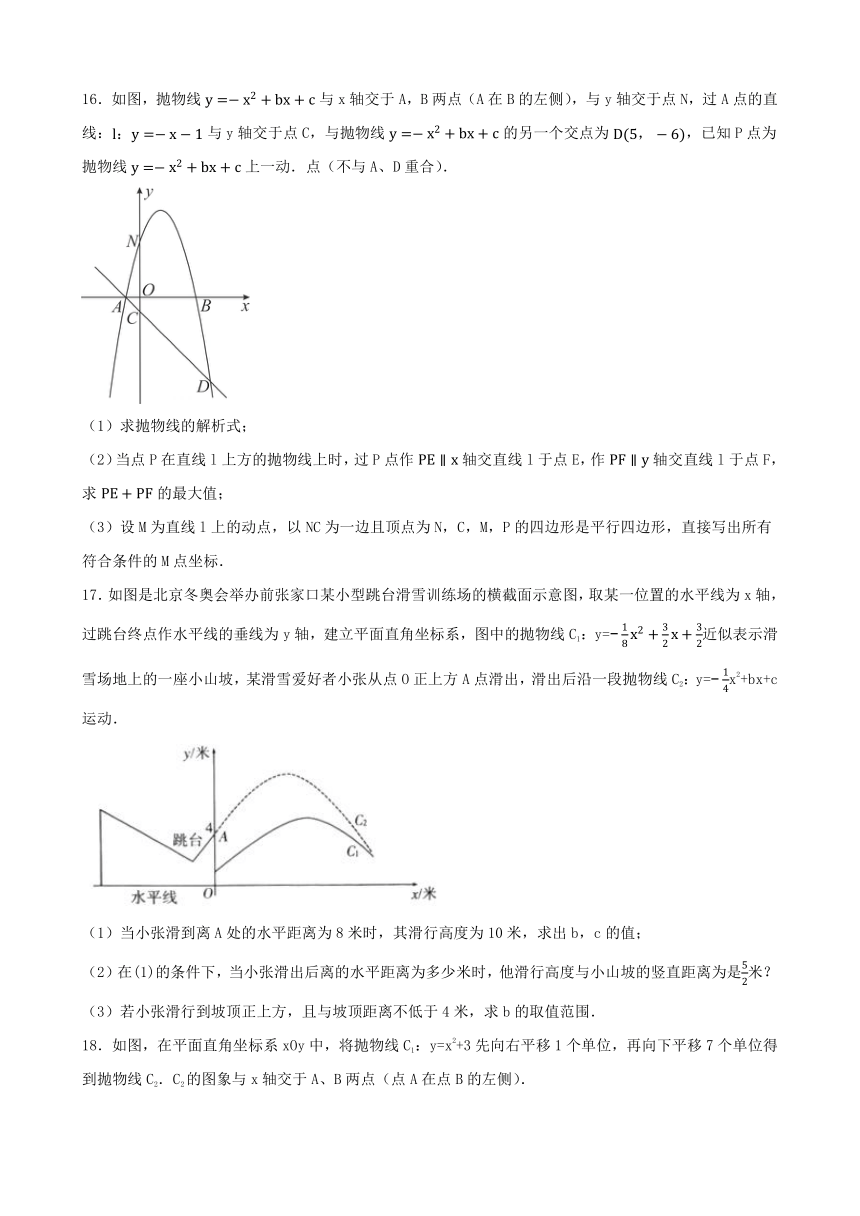
16.如图,抛物线与x轴交于A,B两点(A在B的左侧),与y轴交于点N,过A点的直线:与y轴交于点C,与抛物线的另一个交点为,已知P点为抛物线上一动.点(不与A、D重合).
(1)求抛物线的解析式;
(2)当点P在直线l上方的抛物线上时,过P点作轴交直线l于点E,作轴交直线l于点F,求的最大值;
(3)设M为直线l上的动点,以NC为一边且顶点为N,C,M,P的四边形是平行四边形,直接写出所有符合条件的M点坐标.
17.如图是北京冬奥会举办前张家口某小型跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=近似表示滑雪场地上的一座小山坡,某滑雪爱好者小张从点O正上方A点滑出,滑出后沿一段抛物线C2:y=x2+bx+c运动.
(1)当小张滑到离A处的水平距离为8米时,其滑行高度为10米,求出b,c的值;
(2)在(1)的条件下,当小张滑出后离的水平距离为多少米时,他滑行高度与小山坡的竖直距离为是米?
(3)若小张滑行到坡顶正上方,且与坡顶距离不低于4米,求b的取值范围.
18.如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2.C2的图象与x轴交于A、B两点(点A在点B的左侧).
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形?如果存在,请求出点G的坐标;如果不存在,请说明理由.
参考答案
1.A
2.D
3.C
4.B
5.C
6.D
7.A
8.B
9.2
10.(0,4)
11.a>2
12.
13.
14.(1)解:把和代入
,解得
∴抛物线的表达式为
∴当时,
∴点C的坐标是
(2)解:
设平移后的抛物线表达式为
把代入得
解得
∵,
∴
15.解:由题意
(1)
故与的函数关系式为:
(2)根据题意,当天销售利润恰好240元,
∴
解得,
当天销售单价为或元.
(3)∵每件文具利润不超过
∴,得
∴文具的销售单价为,
由(1)得
∵对称轴为
∴在对称轴的左侧,且随着的增大而增大
∴当时,取得最大值,此时
即每件文具售价为9元时,最大利润为280元
16.(1)解:直线过点A,
,
又,
将点A,D的坐标代入抛物线表达式可得:,
解得.
抛物线的解析式为:.
(2)解:如图,
设点,
轴,轴,
则,
点P在直线l上方的抛物线上,
,
,,
.
当时,取得最大值,最大值为18.
(3)符合条件的M点有三个:.
17.(1)解:由题意可知抛物线C2:y=x2 +bx+c过点(0, 4)和(8, 10)
将其代入得:
解得,
∴b=,c=4
(2)解:由(1)可得抛物线Cq解析式为: y=x2+x+4 ,
设运动员运动的水平距离为m米时,运动员与小山坡的竖直距离为米,依题意得:
解得: m1=10,m2=0(舍),
故运动员运动的水平距离为10米时,运动员与小山坡的竖直距离为为米.
(3)解:∵抛物线C2经过点(0, 4),
∴c=4,
抛物线C1: y==
当x=6时,运动员到达坡项,
即×62 +6b+4≥4+6.
∴b≥
18.(1)解:∵将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2,
∴抛物线C1的顶点(0,3)向右平移1个单位,再向下平移7个单位得到(1,﹣4).
∴抛物线C2的顶点坐标为(1,﹣4).
∴抛物线C2的解析式为y=(x﹣1)2﹣4,
即y=x2﹣2x﹣3;
(2)解:证明:由x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∵点A在点B的左侧,
∴A(﹣1,0),B(3,0),AB=4.
∵抛物线C2的对称轴为x=1,顶点坐标D为(1,﹣4),
∴CD=4.AC=CB=2.
将x=1代入y=x2+3得y=4,
∴E(1,4),CE=CD.
∴四边形ADBE是平行四边形.
∵ED⊥AB,
∴四边形ADBE是菱形.
S菱形ADBE=2× ×AB×CE=2× ×4×4=16.
(3)解:存在.分OB为平行四边形的边和对角线两种情况:
①当OB为平行四边形的一边时,如图1,
设F(1,y),
∵OB=3,∴G1(﹣2,y)或G2(4,y).
∵点G在y=x2﹣2x﹣3上,
∴将x=﹣2代入,得y=5;将x=4代入,得y=5.
∴G1(﹣2,5),G2(4,5).
②当OB为平行四边形的一对角线时,如图2,
设F(1,y),OB的中点M,过点G作GH⊥OB于点H,
∵OB=3,OC=1,∴OM= ,CM= .
∵△CFM≌△HGM(AAS),∴HM=CM= .∴OH=2.
∴G3(2,﹣y).
∵点G在y=x2﹣2x﹣3上,
∴将(2,﹣y)代入,得﹣y=﹣3,即y=3.
∴G3(2,﹣3).
综上所述,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,点G的坐标为G1(﹣2,5),G2(4,5),G3(2,﹣3).
一、选择题
1.下列函数中属于二次函数的是( )
A. B.
C. D.
2.把抛物线向右平移3个单位,再向下平移2个单位,得到抛物线( )
A. B.
C. D.
3.关于的图象,下列叙述正确的是( )
A.顶点坐标为 B.对称轴为直线
C.当时,随的增大而增大 D.开口向下
4.若抛物线经过点,则该抛物线一定还经过点( )
A. B. C. D.
5.已知二次函数的图象经过点和.若,则的取值范围是( )
A. B.
C.或 D.
6.已知y=ax+b的图象如图所示,则y=ax2+bx的图象有可能是( )
A. B. C. D.
7.已知,抛物线与一个交点为.规定:当时,;当时,;下列结论:①有最小值3;②关于函数图象关于直线对称;③直线与关于的函数图象有4个交点;④当时,随的增大而减小.其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
8.如图所示,一座抛物线形的拱桥在正常水位时,水面AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD,那么CD宽为( )
A.4米 B.10米 C.4米 D.12米
二、填空题
9.若函数是二次函数,则 .
10.二次函数y=﹣2x2+3x+4的图象与y轴的交点坐标是 .
11.若二次函数有最大值,则的取值范围是 .
12.已知关于的二次函数,无论取何值,函数图象恒过定点,则点的坐标为 .
13.已知二次函数的图象与轴交于两点.若,则 .
三、解答题
14.如图,在平面直角坐标系中,抛物线与x轴交于点和,与y轴交于点C.
(1)求此抛物线的表达式及点C的坐标;
(2)将此抛物线沿x轴向左平移个单位得到新抛物线,且新抛物线仍经过点C,求m的值.
15.我市某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨1元,当天的销售量就减少10件.设当天销售单价统一为x元/件,当天销售利润为y元.
(1)求y与x的函数关系式(不要求写出自变量的取值范围);
(2)若当天销售利润恰好240元,求当天销售单价;
(3)若每件文具的利润不超过,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
16.如图,抛物线与x轴交于A,B两点(A在B的左侧),与y轴交于点N,过A点的直线:与y轴交于点C,与抛物线的另一个交点为,已知P点为抛物线上一动.点(不与A、D重合).
(1)求抛物线的解析式;
(2)当点P在直线l上方的抛物线上时,过P点作轴交直线l于点E,作轴交直线l于点F,求的最大值;
(3)设M为直线l上的动点,以NC为一边且顶点为N,C,M,P的四边形是平行四边形,直接写出所有符合条件的M点坐标.
17.如图是北京冬奥会举办前张家口某小型跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=近似表示滑雪场地上的一座小山坡,某滑雪爱好者小张从点O正上方A点滑出,滑出后沿一段抛物线C2:y=x2+bx+c运动.
(1)当小张滑到离A处的水平距离为8米时,其滑行高度为10米,求出b,c的值;
(2)在(1)的条件下,当小张滑出后离的水平距离为多少米时,他滑行高度与小山坡的竖直距离为是米?
(3)若小张滑行到坡顶正上方,且与坡顶距离不低于4米,求b的取值范围.
18.如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2.C2的图象与x轴交于A、B两点(点A在点B的左侧).
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形?如果存在,请求出点G的坐标;如果不存在,请说明理由.
参考答案
1.A
2.D
3.C
4.B
5.C
6.D
7.A
8.B
9.2
10.(0,4)
11.a>2
12.
13.
14.(1)解:把和代入
,解得
∴抛物线的表达式为
∴当时,
∴点C的坐标是
(2)解:
设平移后的抛物线表达式为
把代入得
解得
∵,
∴
15.解:由题意
(1)
故与的函数关系式为:
(2)根据题意,当天销售利润恰好240元,
∴
解得,
当天销售单价为或元.
(3)∵每件文具利润不超过
∴,得
∴文具的销售单价为,
由(1)得
∵对称轴为
∴在对称轴的左侧,且随着的增大而增大
∴当时,取得最大值,此时
即每件文具售价为9元时,最大利润为280元
16.(1)解:直线过点A,
,
又,
将点A,D的坐标代入抛物线表达式可得:,
解得.
抛物线的解析式为:.
(2)解:如图,
设点,
轴,轴,
则,
点P在直线l上方的抛物线上,
,
,,
.
当时,取得最大值,最大值为18.
(3)符合条件的M点有三个:.
17.(1)解:由题意可知抛物线C2:y=x2 +bx+c过点(0, 4)和(8, 10)
将其代入得:
解得,
∴b=,c=4
(2)解:由(1)可得抛物线Cq解析式为: y=x2+x+4 ,
设运动员运动的水平距离为m米时,运动员与小山坡的竖直距离为米,依题意得:
解得: m1=10,m2=0(舍),
故运动员运动的水平距离为10米时,运动员与小山坡的竖直距离为为米.
(3)解:∵抛物线C2经过点(0, 4),
∴c=4,
抛物线C1: y==
当x=6时,运动员到达坡项,
即×62 +6b+4≥4+6.
∴b≥
18.(1)解:∵将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2,
∴抛物线C1的顶点(0,3)向右平移1个单位,再向下平移7个单位得到(1,﹣4).
∴抛物线C2的顶点坐标为(1,﹣4).
∴抛物线C2的解析式为y=(x﹣1)2﹣4,
即y=x2﹣2x﹣3;
(2)解:证明:由x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∵点A在点B的左侧,
∴A(﹣1,0),B(3,0),AB=4.
∵抛物线C2的对称轴为x=1,顶点坐标D为(1,﹣4),
∴CD=4.AC=CB=2.
将x=1代入y=x2+3得y=4,
∴E(1,4),CE=CD.
∴四边形ADBE是平行四边形.
∵ED⊥AB,
∴四边形ADBE是菱形.
S菱形ADBE=2× ×AB×CE=2× ×4×4=16.
(3)解:存在.分OB为平行四边形的边和对角线两种情况:
①当OB为平行四边形的一边时,如图1,
设F(1,y),
∵OB=3,∴G1(﹣2,y)或G2(4,y).
∵点G在y=x2﹣2x﹣3上,
∴将x=﹣2代入,得y=5;将x=4代入,得y=5.
∴G1(﹣2,5),G2(4,5).
②当OB为平行四边形的一对角线时,如图2,
设F(1,y),OB的中点M,过点G作GH⊥OB于点H,
∵OB=3,OC=1,∴OM= ,CM= .
∵△CFM≌△HGM(AAS),∴HM=CM= .∴OH=2.
∴G3(2,﹣y).
∵点G在y=x2﹣2x﹣3上,
∴将(2,﹣y)代入,得﹣y=﹣3,即y=3.
∴G3(2,﹣3).
综上所述,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,点G的坐标为G1(﹣2,5),G2(4,5),G3(2,﹣3).
同课章节目录
