18.2 特殊的平行四边形 导学案
文档属性
| 名称 | 18.2 特殊的平行四边形 导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 62.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-18 00:00:00 | ||
图片预览



文档简介
18.2.1 矩形的性质
【学习目标】
1、理解矩形的概念,掌握矩形的性质定理和直角三角形的性质定理
2、能熟练应用矩形的性质进行有关的证明与计算;
3、 养成规范的思维方式和推理意识.
【重点】矩形的概念、性质.
【难点】灵活运用矩形的概念和性质进行推理和计算
预 习 案
预习自学
1、给出一个□ABCD,固定它的四条边的长度,如果改变其中一个内角(如∠B)的大小,它还是平行四边形吗?为什么?
2、当∠B的大小变化时,其他三个内角与∠B的数量关系是什么?如果当∠B成为直角时,得到什么样的图形?
归纳:矩形的定义: 。
1. 如图,已知四边形ABCD是矩形,它具有平行四边形的所有性质,此外,矩形还具有哪些特殊的性质?请找出来,并给出证明。
归纳总结:矩形的性质定理:
2.矩形ABCD的两条对角线交于点O,沿对 ( http: / / www.21cnjy.com )角线AC将矩形剪开,得到Rt△ABC(如图).通过这个图形你发现了直角三角形的一个怎样的性质?请给出证明.
归纳总结:直角三角形的性质定理2:
探 究 案
探究点一:矩形性质定理的应用(培养分析问题的能力)
例1.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,O为对角线AC、BD的交点,且∠CAE=15°.
(1)求证:△AOB为等边三角形;
(2)求证:BO=BE;
(3)求∠BOE度数.
【针对性练习】
1. 矩形的两条对角线的夹角为60°,一条对角线与短边的和为15cm,则短边的边长为 cm.
2. 矩形一个角的平分线分矩形一边为1cm和3cm两部分,则这个矩形的面积
为 cm2.
探究点二:直角三角形性质定理的应用(培养分析问题的能力)
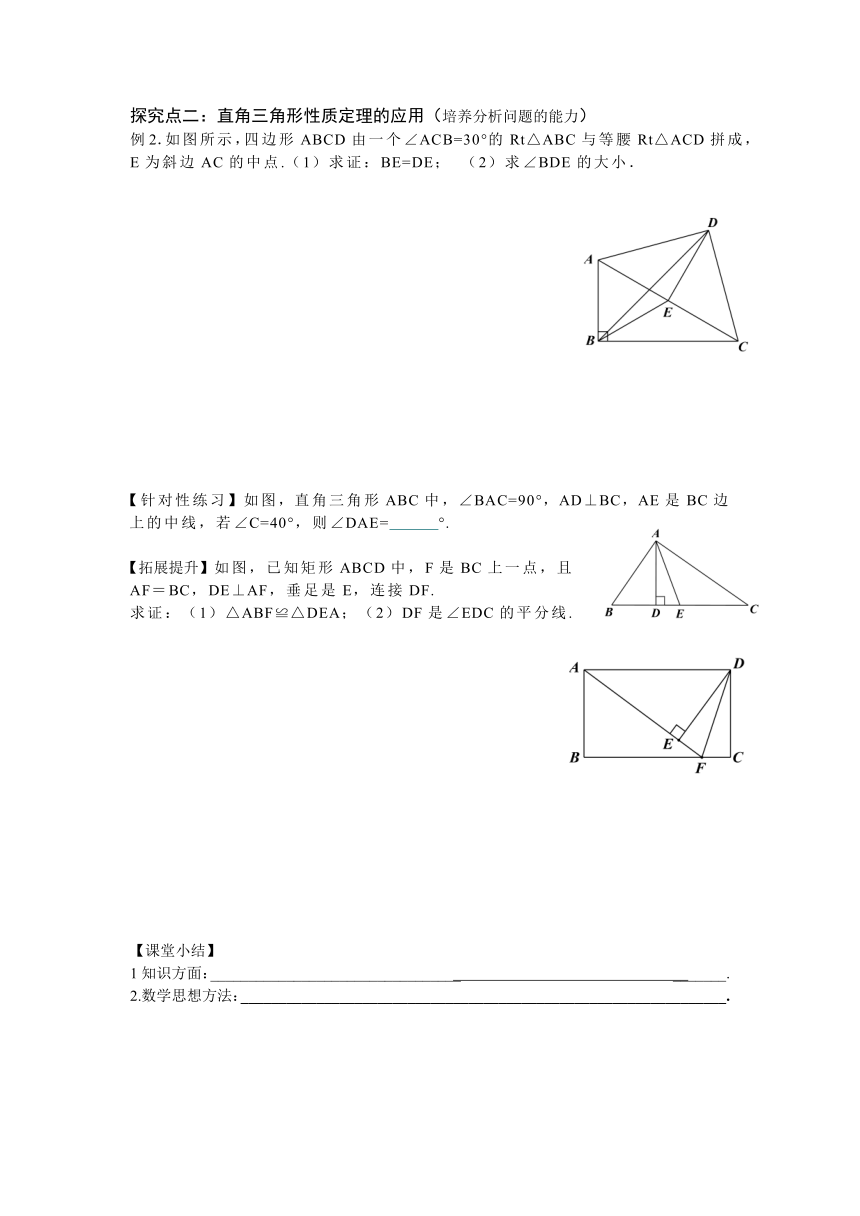
例2.如图所示,四边形ABCD由一个∠AC ( http: / / www.21cnjy.com )B=30°的Rt△ABC与等腰Rt△ACD拼成,E为斜边AC的中点.(1)求证:BE=DE; (2)求∠BDE的大小.
【针对性练习】如图,直角三 ( http: / / www.21cnjy.com )角形ABC中,∠BAC=90°,AD⊥BC,AE是BC边上的中线,若∠C=40°,则∠DAE= °.
【拓展提升】如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.
求证:(1)△ABF≌△DEA;(2)DF是∠EDC的平分线.
【课堂小结】
1知识方面:_________________________________ _______.
2.数学思想方法:________________________________________________________________.
18.2.2 矩形的判定
【学习目标】
理解并掌握矩形的判定定理。
使学生能应用矩形的定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力。
3. 自主学习,合作探究,体验数学命题探究和发现的过程.
【重点】矩形判定定理的探究及应用.
【难点】灵活运用矩形的性质和判定定理进行推理论证
预 习 案
预习自学
根据矩形的定义,我们研究了矩形的性质,那么如何来判定一个四边形是矩形呢?除了定义外,还有什么方法吗?
1.我们知道矩形的对角线相等,反过来对角线相等的平行四边形是举行吗?这个命题是否为真命题?如果是,写出证明过程.(写出已知、求证及证明)
归纳总结:矩形的判定定理1:
2.如图,四边形ABCD中,∠A,∠B和∠C都是直角,你能证明四边形ABCD是矩形吗?如果能,写出证明过程.
归纳总结:矩形的判定定理2:
思考:如果上面定理只从对角线之间的关系上来说的话,还可以如何叙述?
3.目前为止我们知道的判定矩形的方法有哪些?
探 究 案
探究点一:矩形判定定理的应用
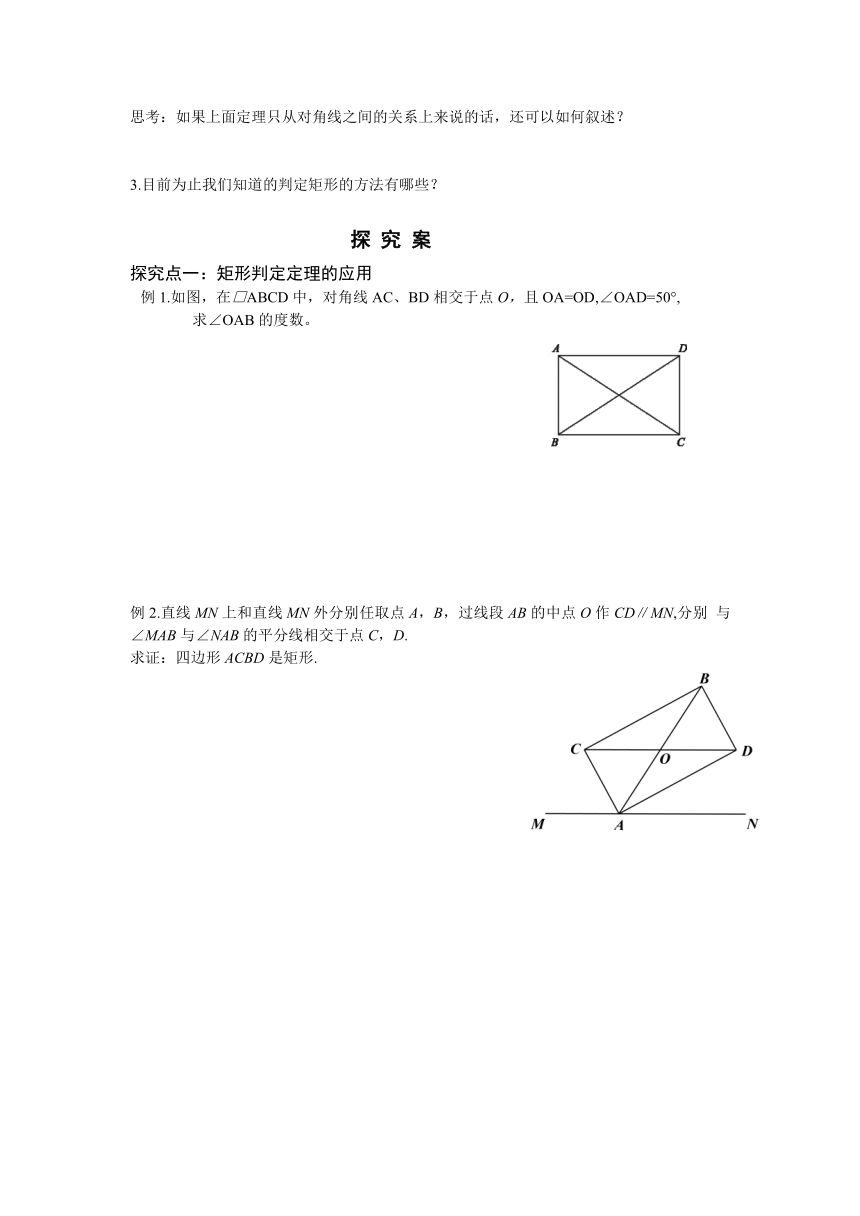
例1.如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=50°,
求∠OAB的度数。
例2.直线MN上和直线MN外分别任取点A,B,过线段AB的中点O作CD∥MN,分别 与∠MAB与∠NAB的平分线相交于点C,D.
求证:四边形ACBD是矩形.
探究点二:直角三角形的性质定理和矩形判定定理的综合应用
例2.已知:如图,□ABCD中,以AC为斜边作Rt△AMC,且∠BMD为直角.
求证:四边形ABCD是矩形.
小结:判定一个四边形是矩形的基本思路:
.
【针对性练习】已知点A、B、C、D在同一平面 ( http: / / www.21cnjy.com )内,有6个条件:①AB∥CD,②AB=CD,③BC∥AD,④BC=AD,⑤AC=不断、,⑥∠A=90°.从这6个条件中选出_______3个,能使四边形ABCD是矩形.(答案不唯一,请尽可能多的写出)
【拓展提升】
如图,△ABC中,点O是AC上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论.
【课堂小结】
1知识方面:_________________________________ _______.
2.数学思想方法:___ ( http: / / www.21cnjy.com )_____________________________________________________________.
18.2.2 菱形第1课时
一、学习目标:
1.掌握菱形概念,知道菱形与平行四边形的关系.
2.理解并掌握菱形的定义及性质1、2;会用这些性质进行有关的论证和计算,会计算菱形的面积.
3.通过运用菱形知识解决具体问题,提高分析能力和观察能力.
二、重点、难点
1.教学重点:菱形的性质
2.教学难点:菱形的性质及菱形知识的综合应用.
预习自学
1.什么叫做平行四边形?什么叫矩形?平行四边形和矩形之间的关系是什么?
2.(引入)我们已经学习了一种特殊的平 ( http: / / www.21cnjy.com )行四边形——矩形,其实还有另外的特殊平行四边形,教师演示:(可将事先按如图做成的一组对边可以活动的教具进行演示)如图,改变平行四边形的边,使之一组邻边相等,从而引出菱形概念.
( http: / / www.21cnjy.com )
菱形定义: .
【强调】 菱形(1)是平行四边形;(2)一组邻边相等.
举一些日常生活中所见到过的菱形的例子.
1. 如图,已知四边形ABCD是菱 ( http: / / www.21cnjy.com )形,它具有平行四边形的所有性质,此外,菱形还具有哪些特殊的性质?请找出来,并给出证明。(自己画图并证明)
归纳总结:菱形的性质定理:
.
用几何符号表示 :
例2(补充)【菱形的面积公式】思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积公式吗
证明:
自学(教材P56例3)
五、随堂练习
1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为 .
2.已知菱形的两条对角线分别是6cm和8cm ,求菱形的周长和面积.
3.已知菱形ABCD的周长为20cm,且相邻两内角之比是1∶2,求菱形的对角线的长和面积.
4.已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.
六、课后练习
1.菱形ABCD中,∠D∶∠A=3∶1,菱形的周长为 8cm,求菱形的高.
2.已知,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm,求(1)对角线AC的长度;(2)菱形ABCD的面积.
18.2.2 菱形的判定(二)
学习目标:
1.理解并掌握菱形两个判定方法;会用这些判定方法进行有关的论证和计算;
2.在菱形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.
一、复习:菱形有哪些特殊性质?
边:__________________________;______________________________
角:__________________________;______________________________
对角线:_____________________________;___________________________________
二、合作探究
(菱形的判定方法1)菱形的定义:
有 的 叫做菱形.
.用符号语言可以表示为:
∵四边形ABCD是 四边形 ∵ ___ =____, ∴□ ABCD是菱形
2.探究菱形的判定方法2
思考:我们知道,菱形的四条边相等.反过来,四条边相等的四边形是菱形吗
结论: .
证明结论:
已知:如上图,在四边形_______中,____=____=____=____
求证:四边形ABCD是_____.
证明:
总结菱形的判定方法2:_______ .
利用上图用符号语言表示为:在四边形ABCD中,
∵ ____=____=____=____ ∴四边形ABCD是 形
3.探究菱形的判定方法3
思考:我们知道,菱形的对角线互相垂直,反过来对角线互相垂直的平行四边形是菱形吗
结论: .
请利用下图证明你的猜想:
已知:如图,在□ABCD中,AC和BD是对角线,并且AC⊥BD于点O,求证:□ABCD是菱形.
( http: / / www.21cnjy.com )
总结菱形判定方法3:
利用上图用符号语言可以表示为:∵四边形ABCD是平行四边形,∵AC___BD,∴□ABCD是菱形
归纳菱形的判定定理:
1. ;
2. ;
3. .
三巩固练习
1.判断题,对的画“√”错的画“×”
(1).对角线互相垂直的四边形是菱形( )
(2).对角线垂直的平行四边形是菱形( )
(3)..对角线互相垂直且平分的四边形是菱形( )
(4).对角线相等的四边形是菱形( )
2.□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
3.已知:如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
( http: / / www.21cnjy.com )
4.如图在△ABC中,AD平分∠BAC交BC于D点,过D作DE∥AC交AB于E点, 过D作DF∥AB交AC于F点.
求证:四边形AEDF是菱形
( http: / / www.21cnjy.com )
课后反思:
A
D
M
B
A
B
C
D
O
A
B
C
D
【学习目标】
1、理解矩形的概念,掌握矩形的性质定理和直角三角形的性质定理
2、能熟练应用矩形的性质进行有关的证明与计算;
3、 养成规范的思维方式和推理意识.
【重点】矩形的概念、性质.
【难点】灵活运用矩形的概念和性质进行推理和计算
预 习 案
预习自学
1、给出一个□ABCD,固定它的四条边的长度,如果改变其中一个内角(如∠B)的大小,它还是平行四边形吗?为什么?
2、当∠B的大小变化时,其他三个内角与∠B的数量关系是什么?如果当∠B成为直角时,得到什么样的图形?
归纳:矩形的定义: 。
1. 如图,已知四边形ABCD是矩形,它具有平行四边形的所有性质,此外,矩形还具有哪些特殊的性质?请找出来,并给出证明。
归纳总结:矩形的性质定理:
2.矩形ABCD的两条对角线交于点O,沿对 ( http: / / www.21cnjy.com )角线AC将矩形剪开,得到Rt△ABC(如图).通过这个图形你发现了直角三角形的一个怎样的性质?请给出证明.
归纳总结:直角三角形的性质定理2:
探 究 案
探究点一:矩形性质定理的应用(培养分析问题的能力)
例1.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,O为对角线AC、BD的交点,且∠CAE=15°.
(1)求证:△AOB为等边三角形;
(2)求证:BO=BE;
(3)求∠BOE度数.
【针对性练习】
1. 矩形的两条对角线的夹角为60°,一条对角线与短边的和为15cm,则短边的边长为 cm.
2. 矩形一个角的平分线分矩形一边为1cm和3cm两部分,则这个矩形的面积
为 cm2.
探究点二:直角三角形性质定理的应用(培养分析问题的能力)
例2.如图所示,四边形ABCD由一个∠AC ( http: / / www.21cnjy.com )B=30°的Rt△ABC与等腰Rt△ACD拼成,E为斜边AC的中点.(1)求证:BE=DE; (2)求∠BDE的大小.
【针对性练习】如图,直角三 ( http: / / www.21cnjy.com )角形ABC中,∠BAC=90°,AD⊥BC,AE是BC边上的中线,若∠C=40°,则∠DAE= °.
【拓展提升】如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.
求证:(1)△ABF≌△DEA;(2)DF是∠EDC的平分线.
【课堂小结】
1知识方面:_________________________________ _______.
2.数学思想方法:________________________________________________________________.
18.2.2 矩形的判定
【学习目标】
理解并掌握矩形的判定定理。
使学生能应用矩形的定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力。
3. 自主学习,合作探究,体验数学命题探究和发现的过程.
【重点】矩形判定定理的探究及应用.
【难点】灵活运用矩形的性质和判定定理进行推理论证
预 习 案
预习自学
根据矩形的定义,我们研究了矩形的性质,那么如何来判定一个四边形是矩形呢?除了定义外,还有什么方法吗?
1.我们知道矩形的对角线相等,反过来对角线相等的平行四边形是举行吗?这个命题是否为真命题?如果是,写出证明过程.(写出已知、求证及证明)
归纳总结:矩形的判定定理1:
2.如图,四边形ABCD中,∠A,∠B和∠C都是直角,你能证明四边形ABCD是矩形吗?如果能,写出证明过程.
归纳总结:矩形的判定定理2:
思考:如果上面定理只从对角线之间的关系上来说的话,还可以如何叙述?
3.目前为止我们知道的判定矩形的方法有哪些?
探 究 案
探究点一:矩形判定定理的应用
例1.如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=50°,
求∠OAB的度数。
例2.直线MN上和直线MN外分别任取点A,B,过线段AB的中点O作CD∥MN,分别 与∠MAB与∠NAB的平分线相交于点C,D.
求证:四边形ACBD是矩形.
探究点二:直角三角形的性质定理和矩形判定定理的综合应用
例2.已知:如图,□ABCD中,以AC为斜边作Rt△AMC,且∠BMD为直角.
求证:四边形ABCD是矩形.
小结:判定一个四边形是矩形的基本思路:
.
【针对性练习】已知点A、B、C、D在同一平面 ( http: / / www.21cnjy.com )内,有6个条件:①AB∥CD,②AB=CD,③BC∥AD,④BC=AD,⑤AC=不断、,⑥∠A=90°.从这6个条件中选出_______3个,能使四边形ABCD是矩形.(答案不唯一,请尽可能多的写出)
【拓展提升】
如图,△ABC中,点O是AC上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论.
【课堂小结】
1知识方面:_________________________________ _______.
2.数学思想方法:___ ( http: / / www.21cnjy.com )_____________________________________________________________.
18.2.2 菱形第1课时
一、学习目标:
1.掌握菱形概念,知道菱形与平行四边形的关系.
2.理解并掌握菱形的定义及性质1、2;会用这些性质进行有关的论证和计算,会计算菱形的面积.
3.通过运用菱形知识解决具体问题,提高分析能力和观察能力.
二、重点、难点
1.教学重点:菱形的性质
2.教学难点:菱形的性质及菱形知识的综合应用.
预习自学
1.什么叫做平行四边形?什么叫矩形?平行四边形和矩形之间的关系是什么?
2.(引入)我们已经学习了一种特殊的平 ( http: / / www.21cnjy.com )行四边形——矩形,其实还有另外的特殊平行四边形,教师演示:(可将事先按如图做成的一组对边可以活动的教具进行演示)如图,改变平行四边形的边,使之一组邻边相等,从而引出菱形概念.
( http: / / www.21cnjy.com )
菱形定义: .
【强调】 菱形(1)是平行四边形;(2)一组邻边相等.
举一些日常生活中所见到过的菱形的例子.
1. 如图,已知四边形ABCD是菱 ( http: / / www.21cnjy.com )形,它具有平行四边形的所有性质,此外,菱形还具有哪些特殊的性质?请找出来,并给出证明。(自己画图并证明)
归纳总结:菱形的性质定理:
.
用几何符号表示 :
例2(补充)【菱形的面积公式】思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积公式吗
证明:
自学(教材P56例3)
五、随堂练习
1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为 .
2.已知菱形的两条对角线分别是6cm和8cm ,求菱形的周长和面积.
3.已知菱形ABCD的周长为20cm,且相邻两内角之比是1∶2,求菱形的对角线的长和面积.
4.已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.
六、课后练习
1.菱形ABCD中,∠D∶∠A=3∶1,菱形的周长为 8cm,求菱形的高.
2.已知,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm,求(1)对角线AC的长度;(2)菱形ABCD的面积.
18.2.2 菱形的判定(二)
学习目标:
1.理解并掌握菱形两个判定方法;会用这些判定方法进行有关的论证和计算;
2.在菱形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.
一、复习:菱形有哪些特殊性质?
边:__________________________;______________________________
角:__________________________;______________________________
对角线:_____________________________;___________________________________
二、合作探究
(菱形的判定方法1)菱形的定义:
有 的 叫做菱形.
.用符号语言可以表示为:
∵四边形ABCD是 四边形 ∵ ___ =____, ∴□ ABCD是菱形
2.探究菱形的判定方法2
思考:我们知道,菱形的四条边相等.反过来,四条边相等的四边形是菱形吗
结论: .
证明结论:
已知:如上图,在四边形_______中,____=____=____=____
求证:四边形ABCD是_____.
证明:
总结菱形的判定方法2:_______ .
利用上图用符号语言表示为:在四边形ABCD中,
∵ ____=____=____=____ ∴四边形ABCD是 形
3.探究菱形的判定方法3
思考:我们知道,菱形的对角线互相垂直,反过来对角线互相垂直的平行四边形是菱形吗
结论: .
请利用下图证明你的猜想:
已知:如图,在□ABCD中,AC和BD是对角线,并且AC⊥BD于点O,求证:□ABCD是菱形.
( http: / / www.21cnjy.com )
总结菱形判定方法3:
利用上图用符号语言可以表示为:∵四边形ABCD是平行四边形,∵AC___BD,∴□ABCD是菱形
归纳菱形的判定定理:
1. ;
2. ;
3. .
三巩固练习
1.判断题,对的画“√”错的画“×”
(1).对角线互相垂直的四边形是菱形( )
(2).对角线垂直的平行四边形是菱形( )
(3)..对角线互相垂直且平分的四边形是菱形( )
(4).对角线相等的四边形是菱形( )
2.□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
3.已知:如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
( http: / / www.21cnjy.com )
4.如图在△ABC中,AD平分∠BAC交BC于D点,过D作DE∥AC交AB于E点, 过D作DF∥AB交AC于F点.
求证:四边形AEDF是菱形
( http: / / www.21cnjy.com )
课后反思:
A
D
M
B
A
B
C
D
O
A
B
C
D
