2024年中考数学专项练习--四边形的动点问题(含答案)
文档属性
| 名称 | 2024年中考数学专项练习--四边形的动点问题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 283.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 00:00:00 | ||
图片预览




文档简介
2024年中考数学专项练习--四边形的动点问题
一、单选题
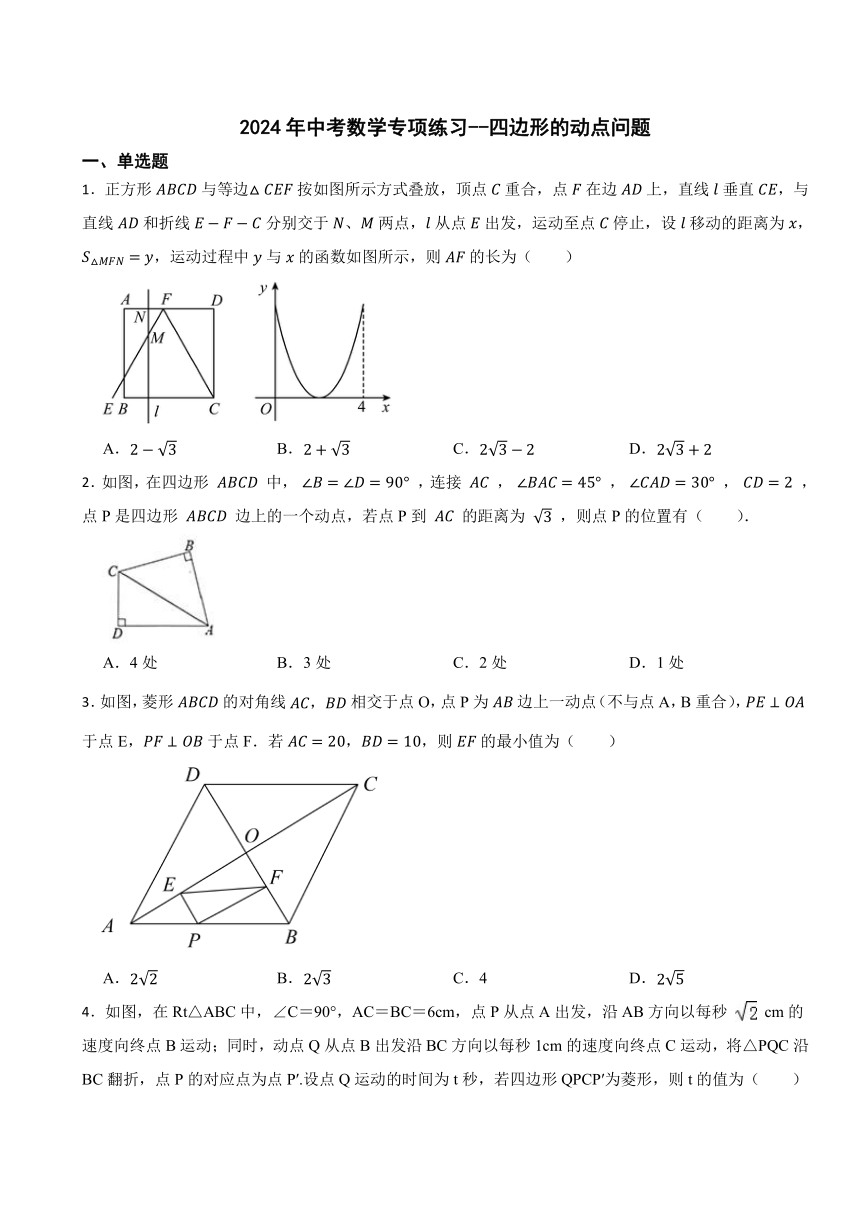
1.正方形与等边按如图所示方式叠放,顶点重合,点在边上,直线垂直,与直线和折线分别交于、两点,从点出发,运动至点停止,设移动的距离为,,运动过程中与的函数如图所示,则的长为( )
A. B. C. D.
2.如图,在四边形 中, ,连接 , , , ,点P是四边形 边上的一个动点,若点P到 的距离为 ,则点P的位置有( ).
A.4处 B.3处 C.2处 D.1处
3.如图,菱形的对角线相交于点O,点P为边上一动点(不与点A,B重合),于点E,于点F.若,,则的最小值为( )
A. B. C.4 D.
4.如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒 cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A. B.2 C.2 D.3
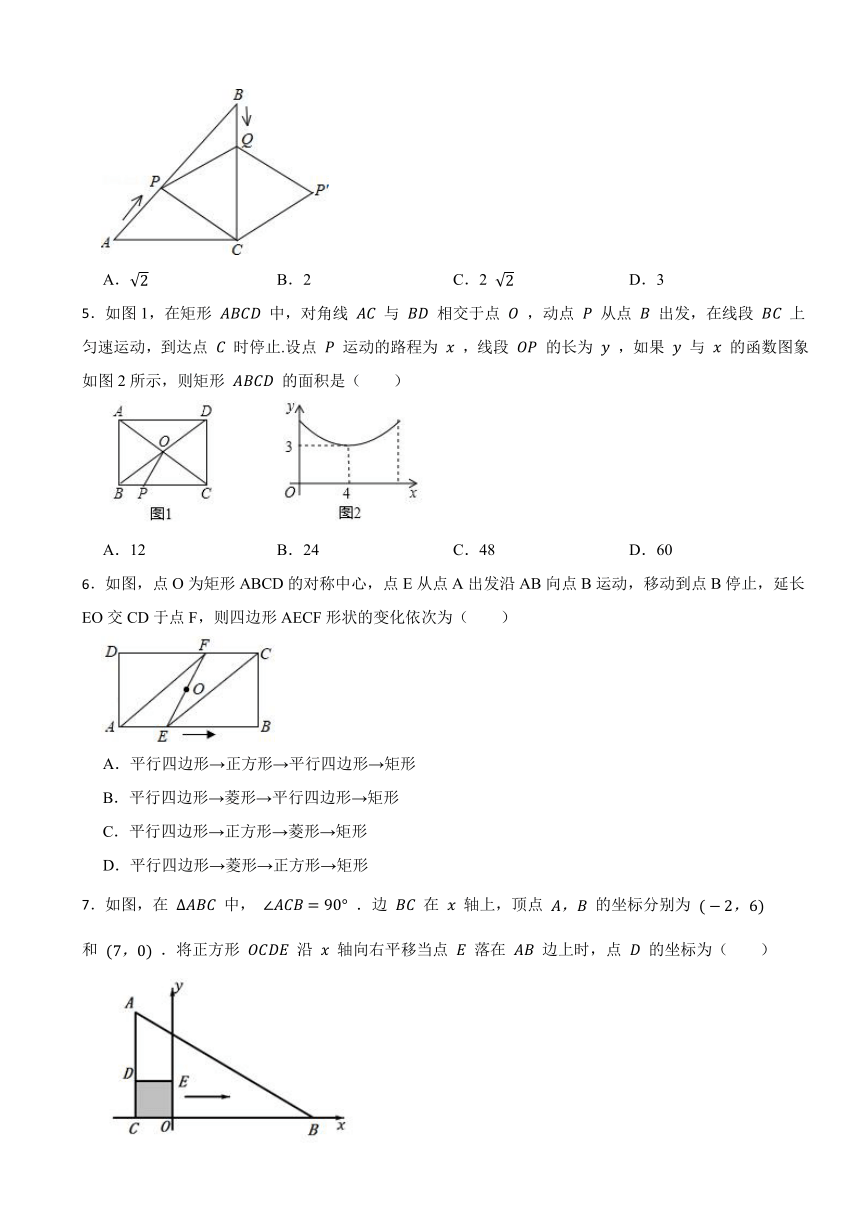
5.如图1,在矩形 中,对角线 与 相交于点 ,动点 从点 出发,在线段 上匀速运动,到达点 时停止.设点 运动的路程为 ,线段 的长为 ,如果 与 的函数图象如图2所示,则矩形 的面积是( )
A.12 B.24 C.48 D.60
6.如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
7.如图,在 中, .边 在 轴上,顶点 的坐标分别为 和 .将正方形 沿 轴向右平移当点 落在 边上时,点 的坐标为( )
A. B. C. D.
8.如图,在正方形ABCD中,已知边长,点E是BC边上一动点(点E不与B、C重合),连接AE,作点B关于直线AE的对称点F,则线段CF的最小值为( )
A.5 B. C. D.
二、填空题
9.如图,菱形ABCD的对角线AC,BD相交于点O,点P为AB边上一动点(不与点A,B重合),于点E,于点F,若,,则EF的最小值为 .
10.如图,在 中, 与 交于点 ,点 在 上, cm, cm, ,点 是 的中点,若点 以1cm/s的速度从点 出发,沿 向点 运动;点 同时以2cm/s的速度从点 出发,沿 向点 运动,点 运动到 点时停止运动,点 也同时停止运动,当点 运动 时,以 、 、 、 为顶点的四边形是平行四边形.
11.如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,点P从B点出发,以每秒1个单位的速度沿着BA边向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为 时,△PAE是以PE为腰的等腰三角形.
12.如图,在矩形中,,E是边上的一动点,连接,过点D作交于点G,垂足为点F,连接BF.
(1)当点G恰为中点时,则 .
(2)当平分时,若,则 .
13.如图,矩形中,,,为边上一动点,以为边构造等边(点位于下方),连接,则
①当时, ;
②点在运动的过程中,的最小值为 .
14.已知四边形ABCD为菱形,其边长为6,,点P在菱形的边AD、CD及对角线AC上运动,当时,则DP的长为 .
三、综合题
15.如图,在△ABC中,BC=4cm,AE∥BC,AE=4cm,点N从点C出发,沿线段CB以2cm/s的速度连续做往返运动,点M从点A出发沿线段AE以1cms的速度运动至点E.M、N两点同时出发,连结MN,MN与AC交于点D,当点M到达点E时,M、N两点同时停止运动,设点M的运动时间为t(s).
(1)当t=3时,线段AM的长度= cm,线段BN的长度= cm.
(2)当BN=AM时,求t的值.
(3)当△ADM≌△CDN时,求出所有满足条件的t值.
16.如图,已知正方形ABCD,AB=2,E是对角线BD上一点,F是射线CB上一点,且EF=EC.
(1)求证:AE=EF;
(2)若BE=AB,请在图2中补全图形,判断AF与EC的位置关系并加以证明;
(3)当点E从点B运动到点D的过程中,求线段FB与BE满足怎样的等量关系.
17.在长方形 中, = , = ,点 从点 开始沿边 向终点 以 的速度移动,与此同时,点 从点 开始沿边 向终点 以 的速度移动.如果 、 分别从 、 同时出发,当点 运动到点 时,两点停止运动.设运动时间为 秒.
(1)填空: = , = (用含t的代数式表示);
(2)当 为何值时, 的长度等于 ?
(3)是否存在 的值,使得五边形 的面积等于 ?若存在,请求出此时 的值;若不存在,请说明理由.
18.在矩形ABCD中,AB=5 cm,BC=6 cm,点P从点A开始沿AB向终点B以1 cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2 cm/s的速度移动,如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,设运动时间为t秒.
(1)填空:BQ= ,PB= (用含t的代数式表示);
(2)当t为何值时,PQ的长度等于 cm
(3)是否存在t的值,使得五边形APQCD的面积等于26 cm2?若存在,请求出此时t的值;若不存在,请说明理由.
19.如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(点P不与A、D重合),PE⊥BP,PE交DC于点E.
(1)求证:△ABP∽△DPE;
(2)设AP=x,DE=y,求y与x之间的函数关系式,并写出x的取值范围;
(3)请你探索在点P运动的过程中,四边形ABED能否构成矩形?如果能,求出AP的长;如果不能,请说明理由.
20.如图,矩形ABCD的边AB=6,AD=9,点E,F分别是边AB,AD上的动点.把△AEF沿直线EF折叠,在同一平面上得到△GEF,点G为点A的对应点.
(1)当点F与点D重合时,求BG的最小值;
(2)当点G落在边BC上的 处时,求BE长.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】B
9.【答案】
10.【答案】3秒或5秒
11.【答案】2或
12.【答案】(1)3
(2)
13.【答案】45°;
14.【答案】2或或
15.【答案】(1)3;2
(2)解:由题意得,AM=t
当0<t≤2时,BN=4-2t,
∴4-2t=t,
解得t= ,
当2<t≤4时,BN=2t-4,
2t-4=t,
解得t=4,
∴t的值为 或4;
(3)解:当0<t≤2时,△ADM≌△CDN,
则AM=CN,即t=2t,
解得t=0,不符合题意,
当2<t≤4时,△ADM≌△CDN,
则AM=CN,即t=4-(2t-4),
解得t= .
16.【答案】(1)证明:∵四边形ABCD是正方形
∴AB=BC=CD=AD,∠ADB=∠CDB=45°
又∵DE=DE
∴△ADE≌△CDE(SAS)
∴AE=EC
∵EF=EC,
∴AE=EF
(2)解:AF∥EC,理由如下:
∵AB=BE=BC,∠ABD=∠DBC=45°
∴∠BAE=∠AEB=∠BEC=∠BCE=67.5°
∵EF=EC
∴∠EFC=∠ECF=67.5°
∴∠FEC=45°,∠BFE=112.5°
∵∠BAE+∠AEF+∠BFE+∠ABF=360°
∴∠AEF=90°,且AE=EF
∴∠AFE=45°
∴∠AFE=∠FEC=45°
∴AF∥EC
(3)解:若点F在点B左侧,如图1,过点E作EM⊥BC,
∵EF=EC,EM⊥BC
∴MC=FM,
∵∠DBC=45°,EM⊥BC
∴BM= BE
∵AB=BC=BM+MC=BM+BF+BM=2BM+BF
∴2= BE+BF
若点P在线段BC上,如图,过点E作EN⊥BC,
∵EF=EC,EN⊥BC
∴FN=NC
∵∠DBC=45°,EN⊥BC
∴BN= BE
∵AB=BC=BN+CN=BN+BN﹣BF=2BN﹣BF
∴2= BE﹣BF
17.【答案】(1);
(2)解:由题意得: = ,
解得: = , = ;
当 = 秒或 秒时, 的长度等于
(3)解:存在 = 秒,能够使得五边形 的面积等于 .理由如下:
长方形 的面积是: = ,
使得五边形 的面积等于 ,则 的面积为 = ,
,
解得: = (不合题意舍去), = .
即当 = 秒时,使得五边形 的面积等于 .
18.【答案】(1)2tcm;(5-t)cm;
(2)由题意得:(5-t)2+(2t)2=( )2,
解得t1=-1(不合题意,舍去),t2=3.
当t=3秒时,PQ的长度等于 cm.
(3)存在.理由如下:
长方形ABCD的面积是:5×6=30(cm2),
使得五边形APQCD的面积等于26 cm2,
则△PBQ的面积为30-26=4(cm2),
∴(5-t)×2t× =4,
解得t1=4(不合题意,舍去),t2=1.
即当t=1秒时,使得五边形APQCD的面积等于26cm2.
19.【答案】(1)证明: ,
,
,
,
,
, ,
,
;
(2)解: ,
,即 ,
则 , ;
(3)解:当四边形 为矩形时, ,即 ,
则 ,
解得, , ,
当 或 时,四边形 能构成矩形.
20.【答案】(1)解:当点F与点D重合时,只有E点运动,
∵把△AEF沿直线EF折叠,在同一平面上得到△GEF
∴AD=DG,
∴G点的运动路径是在以A为圆心,AD长为半径的圆上,
当G、B、D三点共线时,GB最小,
∵AB=6,AD=9,
∴,
∴GB=BD-DG=,
∴BG的最小值为.
(2)解:∵点G落在边BC上的处,如图,
∵BC=9,
∴BG=3,
由题意可知AE=EG,
设EB=x,则AE=6 x,
∴EG=6 x,
在Rt△EGB中,EG2=EB2+GB2,
即(6 x)2=x2+9,
解之:
∴ BE= .
当点G和点C重合时,BG=6,BE=0.
一、单选题
1.正方形与等边按如图所示方式叠放,顶点重合,点在边上,直线垂直,与直线和折线分别交于、两点,从点出发,运动至点停止,设移动的距离为,,运动过程中与的函数如图所示,则的长为( )
A. B. C. D.
2.如图,在四边形 中, ,连接 , , , ,点P是四边形 边上的一个动点,若点P到 的距离为 ,则点P的位置有( ).
A.4处 B.3处 C.2处 D.1处
3.如图,菱形的对角线相交于点O,点P为边上一动点(不与点A,B重合),于点E,于点F.若,,则的最小值为( )
A. B. C.4 D.
4.如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒 cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A. B.2 C.2 D.3
5.如图1,在矩形 中,对角线 与 相交于点 ,动点 从点 出发,在线段 上匀速运动,到达点 时停止.设点 运动的路程为 ,线段 的长为 ,如果 与 的函数图象如图2所示,则矩形 的面积是( )
A.12 B.24 C.48 D.60
6.如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
7.如图,在 中, .边 在 轴上,顶点 的坐标分别为 和 .将正方形 沿 轴向右平移当点 落在 边上时,点 的坐标为( )
A. B. C. D.
8.如图,在正方形ABCD中,已知边长,点E是BC边上一动点(点E不与B、C重合),连接AE,作点B关于直线AE的对称点F,则线段CF的最小值为( )
A.5 B. C. D.
二、填空题
9.如图,菱形ABCD的对角线AC,BD相交于点O,点P为AB边上一动点(不与点A,B重合),于点E,于点F,若,,则EF的最小值为 .
10.如图,在 中, 与 交于点 ,点 在 上, cm, cm, ,点 是 的中点,若点 以1cm/s的速度从点 出发,沿 向点 运动;点 同时以2cm/s的速度从点 出发,沿 向点 运动,点 运动到 点时停止运动,点 也同时停止运动,当点 运动 时,以 、 、 、 为顶点的四边形是平行四边形.
11.如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,点P从B点出发,以每秒1个单位的速度沿着BA边向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为 时,△PAE是以PE为腰的等腰三角形.
12.如图,在矩形中,,E是边上的一动点,连接,过点D作交于点G,垂足为点F,连接BF.
(1)当点G恰为中点时,则 .
(2)当平分时,若,则 .
13.如图,矩形中,,,为边上一动点,以为边构造等边(点位于下方),连接,则
①当时, ;
②点在运动的过程中,的最小值为 .
14.已知四边形ABCD为菱形,其边长为6,,点P在菱形的边AD、CD及对角线AC上运动,当时,则DP的长为 .
三、综合题
15.如图,在△ABC中,BC=4cm,AE∥BC,AE=4cm,点N从点C出发,沿线段CB以2cm/s的速度连续做往返运动,点M从点A出发沿线段AE以1cms的速度运动至点E.M、N两点同时出发,连结MN,MN与AC交于点D,当点M到达点E时,M、N两点同时停止运动,设点M的运动时间为t(s).
(1)当t=3时,线段AM的长度= cm,线段BN的长度= cm.
(2)当BN=AM时,求t的值.
(3)当△ADM≌△CDN时,求出所有满足条件的t值.
16.如图,已知正方形ABCD,AB=2,E是对角线BD上一点,F是射线CB上一点,且EF=EC.
(1)求证:AE=EF;
(2)若BE=AB,请在图2中补全图形,判断AF与EC的位置关系并加以证明;
(3)当点E从点B运动到点D的过程中,求线段FB与BE满足怎样的等量关系.
17.在长方形 中, = , = ,点 从点 开始沿边 向终点 以 的速度移动,与此同时,点 从点 开始沿边 向终点 以 的速度移动.如果 、 分别从 、 同时出发,当点 运动到点 时,两点停止运动.设运动时间为 秒.
(1)填空: = , = (用含t的代数式表示);
(2)当 为何值时, 的长度等于 ?
(3)是否存在 的值,使得五边形 的面积等于 ?若存在,请求出此时 的值;若不存在,请说明理由.
18.在矩形ABCD中,AB=5 cm,BC=6 cm,点P从点A开始沿AB向终点B以1 cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2 cm/s的速度移动,如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,设运动时间为t秒.
(1)填空:BQ= ,PB= (用含t的代数式表示);
(2)当t为何值时,PQ的长度等于 cm
(3)是否存在t的值,使得五边形APQCD的面积等于26 cm2?若存在,请求出此时t的值;若不存在,请说明理由.
19.如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(点P不与A、D重合),PE⊥BP,PE交DC于点E.
(1)求证:△ABP∽△DPE;
(2)设AP=x,DE=y,求y与x之间的函数关系式,并写出x的取值范围;
(3)请你探索在点P运动的过程中,四边形ABED能否构成矩形?如果能,求出AP的长;如果不能,请说明理由.
20.如图,矩形ABCD的边AB=6,AD=9,点E,F分别是边AB,AD上的动点.把△AEF沿直线EF折叠,在同一平面上得到△GEF,点G为点A的对应点.
(1)当点F与点D重合时,求BG的最小值;
(2)当点G落在边BC上的 处时,求BE长.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】B
9.【答案】
10.【答案】3秒或5秒
11.【答案】2或
12.【答案】(1)3
(2)
13.【答案】45°;
14.【答案】2或或
15.【答案】(1)3;2
(2)解:由题意得,AM=t
当0<t≤2时,BN=4-2t,
∴4-2t=t,
解得t= ,
当2<t≤4时,BN=2t-4,
2t-4=t,
解得t=4,
∴t的值为 或4;
(3)解:当0<t≤2时,△ADM≌△CDN,
则AM=CN,即t=2t,
解得t=0,不符合题意,
当2<t≤4时,△ADM≌△CDN,
则AM=CN,即t=4-(2t-4),
解得t= .
16.【答案】(1)证明:∵四边形ABCD是正方形
∴AB=BC=CD=AD,∠ADB=∠CDB=45°
又∵DE=DE
∴△ADE≌△CDE(SAS)
∴AE=EC
∵EF=EC,
∴AE=EF
(2)解:AF∥EC,理由如下:
∵AB=BE=BC,∠ABD=∠DBC=45°
∴∠BAE=∠AEB=∠BEC=∠BCE=67.5°
∵EF=EC
∴∠EFC=∠ECF=67.5°
∴∠FEC=45°,∠BFE=112.5°
∵∠BAE+∠AEF+∠BFE+∠ABF=360°
∴∠AEF=90°,且AE=EF
∴∠AFE=45°
∴∠AFE=∠FEC=45°
∴AF∥EC
(3)解:若点F在点B左侧,如图1,过点E作EM⊥BC,
∵EF=EC,EM⊥BC
∴MC=FM,
∵∠DBC=45°,EM⊥BC
∴BM= BE
∵AB=BC=BM+MC=BM+BF+BM=2BM+BF
∴2= BE+BF
若点P在线段BC上,如图,过点E作EN⊥BC,
∵EF=EC,EN⊥BC
∴FN=NC
∵∠DBC=45°,EN⊥BC
∴BN= BE
∵AB=BC=BN+CN=BN+BN﹣BF=2BN﹣BF
∴2= BE﹣BF
17.【答案】(1);
(2)解:由题意得: = ,
解得: = , = ;
当 = 秒或 秒时, 的长度等于
(3)解:存在 = 秒,能够使得五边形 的面积等于 .理由如下:
长方形 的面积是: = ,
使得五边形 的面积等于 ,则 的面积为 = ,
,
解得: = (不合题意舍去), = .
即当 = 秒时,使得五边形 的面积等于 .
18.【答案】(1)2tcm;(5-t)cm;
(2)由题意得:(5-t)2+(2t)2=( )2,
解得t1=-1(不合题意,舍去),t2=3.
当t=3秒时,PQ的长度等于 cm.
(3)存在.理由如下:
长方形ABCD的面积是:5×6=30(cm2),
使得五边形APQCD的面积等于26 cm2,
则△PBQ的面积为30-26=4(cm2),
∴(5-t)×2t× =4,
解得t1=4(不合题意,舍去),t2=1.
即当t=1秒时,使得五边形APQCD的面积等于26cm2.
19.【答案】(1)证明: ,
,
,
,
,
, ,
,
;
(2)解: ,
,即 ,
则 , ;
(3)解:当四边形 为矩形时, ,即 ,
则 ,
解得, , ,
当 或 时,四边形 能构成矩形.
20.【答案】(1)解:当点F与点D重合时,只有E点运动,
∵把△AEF沿直线EF折叠,在同一平面上得到△GEF
∴AD=DG,
∴G点的运动路径是在以A为圆心,AD长为半径的圆上,
当G、B、D三点共线时,GB最小,
∵AB=6,AD=9,
∴,
∴GB=BD-DG=,
∴BG的最小值为.
(2)解:∵点G落在边BC上的处,如图,
∵BC=9,
∴BG=3,
由题意可知AE=EG,
设EB=x,则AE=6 x,
∴EG=6 x,
在Rt△EGB中,EG2=EB2+GB2,
即(6 x)2=x2+9,
解之:
∴ BE= .
当点G和点C重合时,BG=6,BE=0.
同课章节目录
