2024年中考数学专项练习--切线的判定(含解析)
文档属性
| 名称 | 2024年中考数学专项练习--切线的判定(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 432.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 18:49:53 | ||
图片预览


文档简介
2024年中考数学专项练习--切线的判定
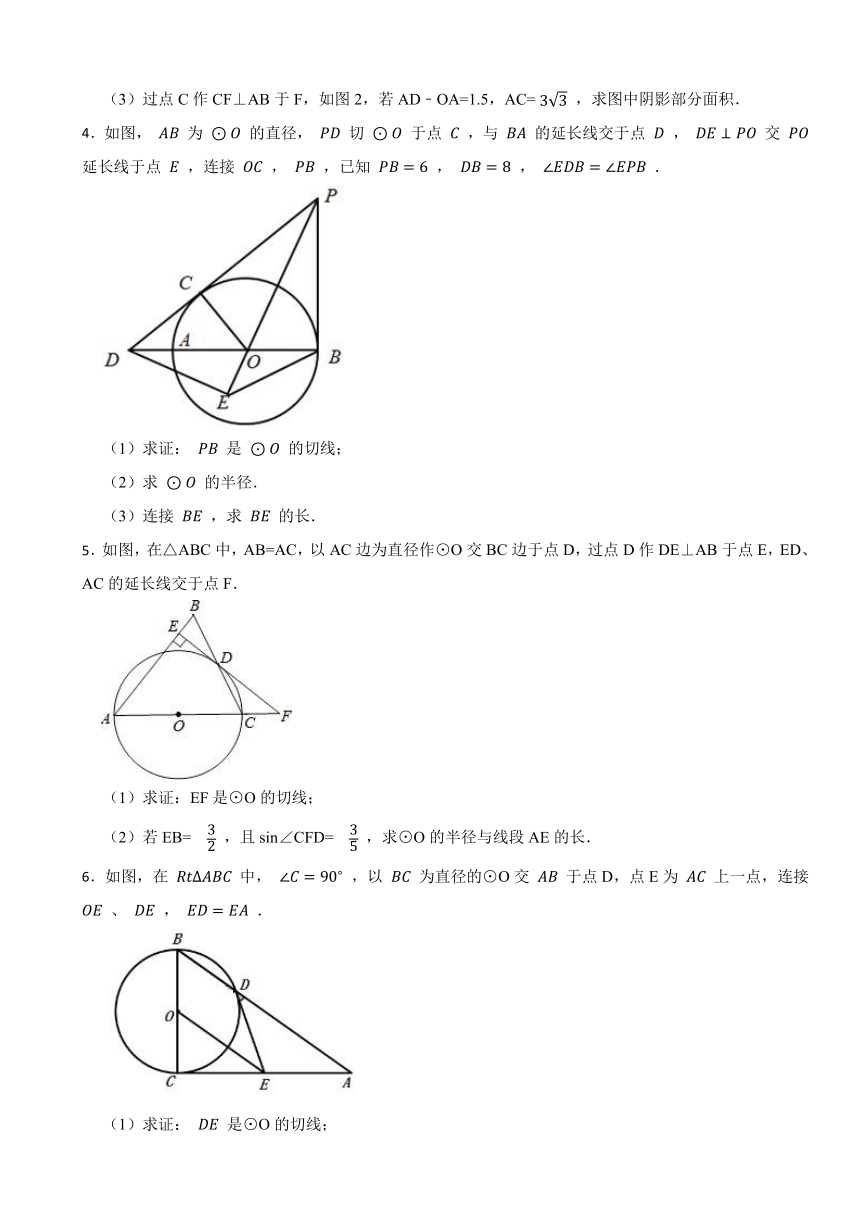
1.如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E,连接OC.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE= ,DE=3,求⊙O的半径及AC的长.
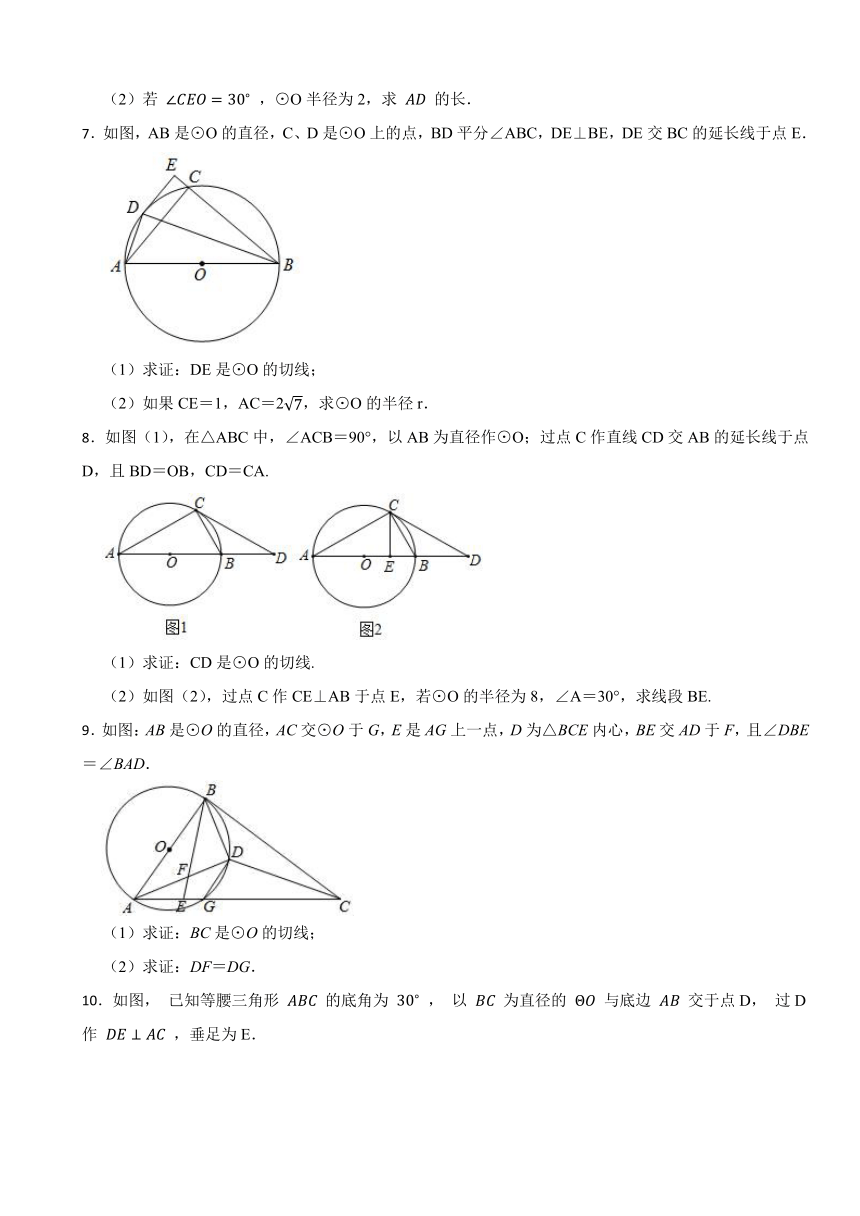
2.如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当弧DC=弧AC时,延长AB至点E,使BE= AB,连接DE.
①求证:DE是⊙O的切线;
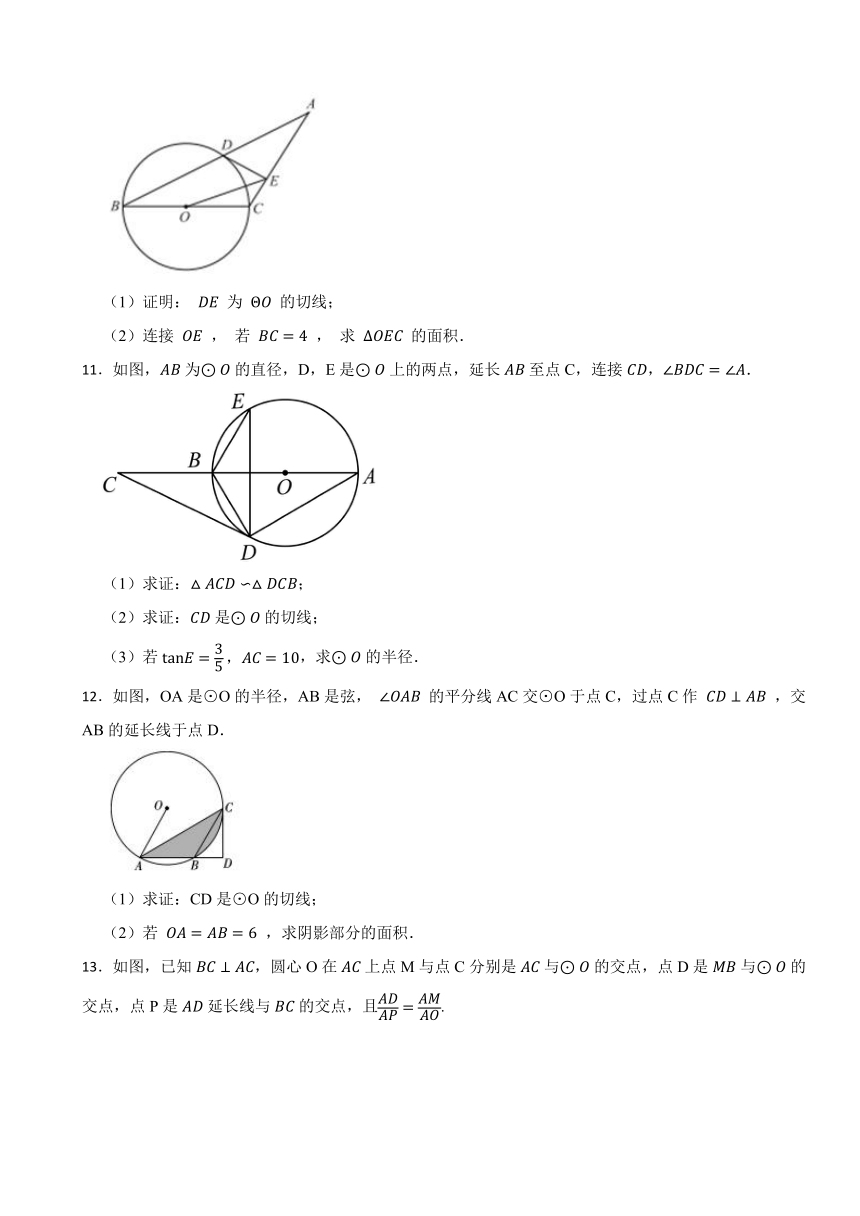
3.如图,AB为⊙O的直径,C,E为O上的两点,若AC平分∠EAB,CD⊥AE于点D.
(1)求证:DC是⊙O切线;
(2)若AO=6,DC= ,求DE的长;
(3)过点C作CF⊥AB于F,如图2,若AD﹣OA=1.5,AC= ,求图中阴影部分面积.
4.如图, 为 的直径, 切 于点 ,与 的延长线交于点 , 交 延长线于点 ,连接 , ,已知 , , .
(1)求证: 是 的切线;
(2)求 的半径.
(3)连接 ,求 的长.
5.如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
(1)求证:EF是⊙O的切线;
(2)若EB= ,且sin∠CFD= ,求⊙O的半径与线段AE的长.
6.如图,在 中, ,以 为直径的⊙O交 于点D,点E为 上一点,连接 、 , .
(1)求证: 是⊙O的切线;
(2)若 ,⊙O半径为2,求 的长.
7.如图,AB是⊙O的直径,C、D是⊙O上的点,BD平分∠ABC,DE⊥BE,DE交BC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果CE=1,AC=2,求⊙O的半径r.
8.如图(1),在△ABC中,∠ACB=90°,以AB为直径作⊙O;过点C作直线CD交AB的延长线于点D,且BD=OB,CD=CA.
(1)求证:CD是⊙O的切线.
(2)如图(2),过点C作CE⊥AB于点E,若⊙O的半径为8,∠A=30°,求线段BE.
9.如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG.
10.如图, 已知等腰三角形 的底角为 , 以 为直径的 与底边 交于点D, 过D作 ,垂足为E.
(1)证明: 为 的切线;
(2)连接 , 若 , 求 的面积.
11.如图,为的直径,D,E是上的两点,延长至点C,连接,.
(1)求证:;
(2)求证:是的切线;
(3)若,求的半径.
12.如图,OA是⊙O的半径,AB是弦, 的平分线AC交⊙O于点C,过点C作 ,交AB的延长线于点D.
(1)求证:CD是⊙O的切线;
(2)若 ,求阴影部分的面积.
13.如图,已知,圆心O在上点M与点C分别是与的交点,点D是与的交点,点P是延长线与的交点,且.
(1)求证:是的切线:
(2)若,,求的值.
14.如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接BD、DE.
(1)求DE是⊙O的切线;
(2)设△CDE的面积为S1,四边形ABED的面积为S2,若S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,连接AE,若⊙O的半径为2,求AE的长.
15.下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程.
已知:如图,⊙O及⊙O上一点P.
求作:过点P的⊙O的切线.
作法:如图,作射线OP;
① 在直线OP外任取一点A,以A为圆心,AP为半径作⊙A,与射线OP交于另一点B;
②连接并延长BA与⊙A交于点C;
③作直线PC;
则直线PC即为所求.根据小元设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵ BC是⊙A的直径,
∴ ∠BPC=90° (填推理依据).
∴ OP⊥PC.
又∵ OP是⊙O的半径,
∴ PC是⊙O的切线 (填推理依据).
16.如图,AB是⊙O的直径, 于点B,连接OC交⊙O于点E,弦 ,弦 于点G.
(1)求证:点E是弧BD的中点;
(2)求证:CD是⊙O的切线;
(3)若 ,⊙O的半径为5,求弦DF的长.
答案解析部分
1.【答案】(1)解:∵CB=CD,CO=CO,OB=OD,
∴△OCB≌△OCD(SSS),
∴∠ODC=∠OBC=90°,
∴OD⊥DC,
∴DC是⊙O的切线;
(2)解:设⊙O的半径为r.
在Rt△OBE中,∵OE2=EB2+OB2,
∴ ,
∴
∴OE=3-1=2
Rt△ABC中,
∴
∴
Rt△BCO中, ,
Rt△ABC中,
2.【答案】(1)解:如图2,连接OD,∵OP⊥PD,PD∥AB,∴∠POB=90°,∵⊙O的直径AB=12,∴OB=OD=6,在Rt△POB中,∠ABC=30°,∴OP=OB tan30°=6× =2 ,
在Rt△POD中,
PD=
(2)解:如图3,连接OD,交CB于点F,连接BD,∵ ,∴∠DBC=∠ABC=30°,∴∠ABD=60°,∵OB=OD,∴△OBD是等边三角形,∴OD⊥FB,∵BE= AB,∴OB=BE,
∴BF∥ED,
∴∠ODE=∠OFB=90°,
∴DE是⊙O的切线
②求PC的长.
解:由①知,OD⊥BC,
∴CF=FB=OB cos30°=6× =3 ,
在Rt△POD中,OF=DF,∴PF= DO=3(直角三角形斜边上的中线,等于斜边的一半),
∴CP=CF﹣PF=3 ﹣3.
3.【答案】(1)解:连接OC,如图1,
∵AC平分∠EAB,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴DC是⊙O切线
(2)解:连接BE交OC于H,如图1,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵OC∥AD,
∴∠OHB=90°,
∴EH=BH,四边形CDEH为矩形,
∴CD=EH=3 ,CH=ED,
∴BH=3 ,
在Rt△OBH中,OH= =3,
∴CH=6-3=3,
∴DE=3
(3)解:连接OC,如图2,设⊙O的半径为r,
∵AC平分∠BAD,CD⊥AD,CF⊥AB,
∴CD=CF,
∴AD=AF=AO+OF,
∵AD-OA=1.5,
∴AO+OF-OA=1.5,即OF=1.5,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAF=∠BAC,
∴△ACF∽△ABC,
∴ ,即 ,
解得r=- (舍去)或r=3,
在Rt△OCF中,cos∠COF= ,
∴∠COF=60°,
∴CF= OF= ,
∴图中阴影部分面积=S扇形BOC-S△OCB= - ×3× = π- .
4.【答案】(1)证明: ,
,
,
,
,
为 的切线
(2)解:在 中, , ,
根据勾股定理得: ,
与 都为 的切线,
;
在 中,设 ,则有 ,
根据勾股定理得:
解得: ,则圆的半径为
(3)解:延长 、 相交于点
与 都为 的切线,
平分
又
,
在 中,
5.【答案】(1)证明:连结OD,如图,
∵AB=AC,
∴∠B=∠ACD,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥EF,
∴EF是⊙O的切线
(2)解:在Rt△ODF,sin∠OFD= = ,
设OD=3x,则OF=5x,
∴AB=AC=6x,AF=8x,
在Rt△AEF中,∵sin∠AFE= = ,
∴AE= 8x= x,
∵BE=AB﹣AE=6x﹣ x= x,
∴ x= ,解得x= ,
∴AE= =6,
OD=3 = ,
即⊙O的半径长为 .
6.【答案】(1)证明:连接 ,
∵ED=EA,
∴∠A=∠ADE,
∵OB=OD,
∴∠OBD=∠BDO,
∵∠ACB=90°,
∴∠A+∠ABC=90°.
∴∠ADE+∠BDO=90°,
∴∠ODE=90,
∴DE是⊙O的切线;
(2)解:连接 ,如图:
∵ED=EA,
∴∠A=∠ADE,
∵BC为直径,
∴∠CDB=∠CDA=90°,
∵∠A+∠ACD=90°,∠ADE+∠CDE=90°,
∴∠ACD=∠CDE,
∴ED=EC,
∴ED=EA=EC,
∴点E为AC中点,
∵点O为BC中点,
∴OE∥AB,
∴∠CEO=∠A=30°,
在 中,∠OCE=90°,OC=2,∠CEO =30°,
∴ ,
∴ ,
在 中,∠ADC=90°, ,∠A =30°,
∴ ,
.
7.【答案】(1)证明:连接OD,如下图所示:
∵OB=OD,
∴∠OBD=∠ODB,
∵BD平分∠ABC,
∴∠OBD=∠DBE,
∴∠ODB=∠DBE,
∴OD∥BE,
∵DE⊥BE于点E,
∴∠E=90°,
∴∠ODE=180°-∠E=180°-90°=90°,
∴OD⊥DE;
∴DE是⊙O的切线.
(2)解:设OD交AC于点M,如下图:
∵AB为⊙O的直径,
∴∠ACB=∠ACE=90°,
由(1)知,∠ODE=90°,
∴∠ACE=∠E=∠ODE=90°,
∴四边形DECM为矩形,
∴EC=DM=1,
∵MO∥CB,O为AC的中点,
∴MO为△ABC的中位线,且∠AMO=∠ACB=90°,
∴AM=MC=AC=,
设圆的半径为r,则MO=DO-DM=r-1,
在Rt△AMO中,由勾股定理可知:AO =AM +MO ,代入数据:
,
解出:,
故圆⊙O的半径为4.
8.【答案】(1)证明:如图1,连结OC,
∵点O为直角三角形斜边AB的中点,
∴OC=OA=OB.
∴点C在⊙O上,
∵BD=OB,
∴AB=DO,
∵CD=CA,
∴∠A=∠D,
∴△ACB≌△DCO,
∴∠DCO=∠ACB=90°,
∴CD是⊙O的切线;
(2)解:如图2,
在Rt△ABC中,BC=ABsin∠A=2×8×sin30°=8,
∵∠ABC=90°-∠A=90°-30°=60°,
∴BE=BCcos60°=8× =4.
9.【答案】(1)证明:∵点D为△BCE的内心,
∴BD平分∠EBC.
∴∠EBD=∠CBD.
又∵∠DBE=∠BAD,
∴∠CBD=∠BAD.
又∵AB是圆的直径,
∴∠BDA=90°.
在Rt△BAD中,∠BAD+∠ABD=90°,
∴∠CBD+∠ABD=90°,即∠ABC=90°.
∴BC⊥AB.
又∵AB为直径,
∴BC是圆的切线;
(2)证明:连接ED,如图,则ED平分∠BEC,
∴∠BED=∠CED.
∵∠EFD为△BFD的外角
∴∠EFD=∠ADB+∠EBD=90°+∠EBD,
又∵四边形ABDG为圆的内接四边形,
∴∠EGD=180°﹣∠ABD=180°﹣(90°﹣∠CDB)=90°+∠CDB
又∵∠EBD=∠CBD,
∴∠EFD=∠EGD
又∵ED=ED,
∴△DFE≌△DGE(AAS ).
∴DF=DG.
10.【答案】(1)证明:连接 .
∵
∴
∵等腰三角形 的底角为30°,即
∴
∴ ∥
∵
∴ ,即 为⊙O的切线.
(2)解:连接 .
∵ ,
∴ ,即 是等边三角形,
∴ , ,
∵ ,
∴ ,
∴ ,
∴ .
11.【答案】(1)证明:∵,,
∴;
(2)证明:连接,
∵为的直径,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵是的半径,
∴是的切线;
(3)解:∵,,,
∴,
∵,
∴,
∵,
∴,,
∴.
∴的半径为.
12.【答案】(1)证明:连接OC,
∵ ,
∴ ,
∵ 平分 ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
又∵ 为 的半径,
∴ 为 的切线.
(2)解:连接OC,
∵ ,又 ,
∴四边形OABC是平行四边形,
∴ ,
∴ ,
∴ ,
又 是等边三角形,
∴ ,
∴ .
13.【答案】(1):证明:连接、、.
,,
,
,
,
,,
,
,
,
,,
,
,
,
,
,
是的切线.
(2)解:连接.由(1)可知:,
,
,
在中,,
,
,
,,
,
,
,
,
,
是的中点,
,
点是的中点,
,
是的直径,
,
在中,,,
,
,,
,
,即,
,
.
14.【答案】(1)证明:连接OD,
∴OD=OB
∴∠ODB=∠OBD.
∵AB是直径,
∴∠ADB=90°,
∴∠CDB=90°.
∵E为BC的中点,
∴DE=BE,
∴∠EDB=∠EBD,
∴∠ODB+∠EDB=∠OBD+∠EBD,
即∠EDO=∠EBO.
∵BC是以AB为直径的⊙O的切线,
∴AB⊥BC,
∴∠EBO=90°,
∴∠ODE=90°,
∴DE是⊙O的切线;
(2)解:∵S2=5S1,
∴S△ADB=2S△CDB,
∴ = ,
∵△BDC∽△ADB,
∴ = ,
∴DB2=AD DC,
∴ ,
∴tan∠BAC= ;
(3)解:∵tan∠BAC= ,
∴ ,得BC= AB=2 ,
∵E为BC的中点,
∴BE= BC= ,
∴AE= .
15.【答案】(1)解:补全图形如图所示,则直线PC即为所求;
(2)圆周角定理;切线的判定
16.【答案】(1)证明:连接OD,
如图
∵ ,
∴ ,
又∵ ,
∴ ,
,
∴ ,
∴ =
∴点E为弧BD的中点
(2)证明:∵在 与 中,
∴ ,
∴ ,
∴CD为⊙О的切线.
(3)解:∵ ,∴ .
设 ,则 ,
在 和 中,
由勾股定理得:
,
解得: .
∴
∴
1.如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E,连接OC.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE= ,DE=3,求⊙O的半径及AC的长.
2.如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当弧DC=弧AC时,延长AB至点E,使BE= AB,连接DE.
①求证:DE是⊙O的切线;
3.如图,AB为⊙O的直径,C,E为O上的两点,若AC平分∠EAB,CD⊥AE于点D.
(1)求证:DC是⊙O切线;
(2)若AO=6,DC= ,求DE的长;
(3)过点C作CF⊥AB于F,如图2,若AD﹣OA=1.5,AC= ,求图中阴影部分面积.
4.如图, 为 的直径, 切 于点 ,与 的延长线交于点 , 交 延长线于点 ,连接 , ,已知 , , .
(1)求证: 是 的切线;
(2)求 的半径.
(3)连接 ,求 的长.
5.如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
(1)求证:EF是⊙O的切线;
(2)若EB= ,且sin∠CFD= ,求⊙O的半径与线段AE的长.
6.如图,在 中, ,以 为直径的⊙O交 于点D,点E为 上一点,连接 、 , .
(1)求证: 是⊙O的切线;
(2)若 ,⊙O半径为2,求 的长.
7.如图,AB是⊙O的直径,C、D是⊙O上的点,BD平分∠ABC,DE⊥BE,DE交BC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果CE=1,AC=2,求⊙O的半径r.
8.如图(1),在△ABC中,∠ACB=90°,以AB为直径作⊙O;过点C作直线CD交AB的延长线于点D,且BD=OB,CD=CA.
(1)求证:CD是⊙O的切线.
(2)如图(2),过点C作CE⊥AB于点E,若⊙O的半径为8,∠A=30°,求线段BE.
9.如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG.
10.如图, 已知等腰三角形 的底角为 , 以 为直径的 与底边 交于点D, 过D作 ,垂足为E.
(1)证明: 为 的切线;
(2)连接 , 若 , 求 的面积.
11.如图,为的直径,D,E是上的两点,延长至点C,连接,.
(1)求证:;
(2)求证:是的切线;
(3)若,求的半径.
12.如图,OA是⊙O的半径,AB是弦, 的平分线AC交⊙O于点C,过点C作 ,交AB的延长线于点D.
(1)求证:CD是⊙O的切线;
(2)若 ,求阴影部分的面积.
13.如图,已知,圆心O在上点M与点C分别是与的交点,点D是与的交点,点P是延长线与的交点,且.
(1)求证:是的切线:
(2)若,,求的值.
14.如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接BD、DE.
(1)求DE是⊙O的切线;
(2)设△CDE的面积为S1,四边形ABED的面积为S2,若S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,连接AE,若⊙O的半径为2,求AE的长.
15.下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程.
已知:如图,⊙O及⊙O上一点P.
求作:过点P的⊙O的切线.
作法:如图,作射线OP;
① 在直线OP外任取一点A,以A为圆心,AP为半径作⊙A,与射线OP交于另一点B;
②连接并延长BA与⊙A交于点C;
③作直线PC;
则直线PC即为所求.根据小元设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵ BC是⊙A的直径,
∴ ∠BPC=90° (填推理依据).
∴ OP⊥PC.
又∵ OP是⊙O的半径,
∴ PC是⊙O的切线 (填推理依据).
16.如图,AB是⊙O的直径, 于点B,连接OC交⊙O于点E,弦 ,弦 于点G.
(1)求证:点E是弧BD的中点;
(2)求证:CD是⊙O的切线;
(3)若 ,⊙O的半径为5,求弦DF的长.
答案解析部分
1.【答案】(1)解:∵CB=CD,CO=CO,OB=OD,
∴△OCB≌△OCD(SSS),
∴∠ODC=∠OBC=90°,
∴OD⊥DC,
∴DC是⊙O的切线;
(2)解:设⊙O的半径为r.
在Rt△OBE中,∵OE2=EB2+OB2,
∴ ,
∴
∴OE=3-1=2
Rt△ABC中,
∴
∴
Rt△BCO中, ,
Rt△ABC中,
2.【答案】(1)解:如图2,连接OD,∵OP⊥PD,PD∥AB,∴∠POB=90°,∵⊙O的直径AB=12,∴OB=OD=6,在Rt△POB中,∠ABC=30°,∴OP=OB tan30°=6× =2 ,
在Rt△POD中,
PD=
(2)解:如图3,连接OD,交CB于点F,连接BD,∵ ,∴∠DBC=∠ABC=30°,∴∠ABD=60°,∵OB=OD,∴△OBD是等边三角形,∴OD⊥FB,∵BE= AB,∴OB=BE,
∴BF∥ED,
∴∠ODE=∠OFB=90°,
∴DE是⊙O的切线
②求PC的长.
解:由①知,OD⊥BC,
∴CF=FB=OB cos30°=6× =3 ,
在Rt△POD中,OF=DF,∴PF= DO=3(直角三角形斜边上的中线,等于斜边的一半),
∴CP=CF﹣PF=3 ﹣3.
3.【答案】(1)解:连接OC,如图1,
∵AC平分∠EAB,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴DC是⊙O切线
(2)解:连接BE交OC于H,如图1,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵OC∥AD,
∴∠OHB=90°,
∴EH=BH,四边形CDEH为矩形,
∴CD=EH=3 ,CH=ED,
∴BH=3 ,
在Rt△OBH中,OH= =3,
∴CH=6-3=3,
∴DE=3
(3)解:连接OC,如图2,设⊙O的半径为r,
∵AC平分∠BAD,CD⊥AD,CF⊥AB,
∴CD=CF,
∴AD=AF=AO+OF,
∵AD-OA=1.5,
∴AO+OF-OA=1.5,即OF=1.5,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAF=∠BAC,
∴△ACF∽△ABC,
∴ ,即 ,
解得r=- (舍去)或r=3,
在Rt△OCF中,cos∠COF= ,
∴∠COF=60°,
∴CF= OF= ,
∴图中阴影部分面积=S扇形BOC-S△OCB= - ×3× = π- .
4.【答案】(1)证明: ,
,
,
,
,
为 的切线
(2)解:在 中, , ,
根据勾股定理得: ,
与 都为 的切线,
;
在 中,设 ,则有 ,
根据勾股定理得:
解得: ,则圆的半径为
(3)解:延长 、 相交于点
与 都为 的切线,
平分
又
,
在 中,
5.【答案】(1)证明:连结OD,如图,
∵AB=AC,
∴∠B=∠ACD,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥EF,
∴EF是⊙O的切线
(2)解:在Rt△ODF,sin∠OFD= = ,
设OD=3x,则OF=5x,
∴AB=AC=6x,AF=8x,
在Rt△AEF中,∵sin∠AFE= = ,
∴AE= 8x= x,
∵BE=AB﹣AE=6x﹣ x= x,
∴ x= ,解得x= ,
∴AE= =6,
OD=3 = ,
即⊙O的半径长为 .
6.【答案】(1)证明:连接 ,
∵ED=EA,
∴∠A=∠ADE,
∵OB=OD,
∴∠OBD=∠BDO,
∵∠ACB=90°,
∴∠A+∠ABC=90°.
∴∠ADE+∠BDO=90°,
∴∠ODE=90,
∴DE是⊙O的切线;
(2)解:连接 ,如图:
∵ED=EA,
∴∠A=∠ADE,
∵BC为直径,
∴∠CDB=∠CDA=90°,
∵∠A+∠ACD=90°,∠ADE+∠CDE=90°,
∴∠ACD=∠CDE,
∴ED=EC,
∴ED=EA=EC,
∴点E为AC中点,
∵点O为BC中点,
∴OE∥AB,
∴∠CEO=∠A=30°,
在 中,∠OCE=90°,OC=2,∠CEO =30°,
∴ ,
∴ ,
在 中,∠ADC=90°, ,∠A =30°,
∴ ,
.
7.【答案】(1)证明:连接OD,如下图所示:
∵OB=OD,
∴∠OBD=∠ODB,
∵BD平分∠ABC,
∴∠OBD=∠DBE,
∴∠ODB=∠DBE,
∴OD∥BE,
∵DE⊥BE于点E,
∴∠E=90°,
∴∠ODE=180°-∠E=180°-90°=90°,
∴OD⊥DE;
∴DE是⊙O的切线.
(2)解:设OD交AC于点M,如下图:
∵AB为⊙O的直径,
∴∠ACB=∠ACE=90°,
由(1)知,∠ODE=90°,
∴∠ACE=∠E=∠ODE=90°,
∴四边形DECM为矩形,
∴EC=DM=1,
∵MO∥CB,O为AC的中点,
∴MO为△ABC的中位线,且∠AMO=∠ACB=90°,
∴AM=MC=AC=,
设圆的半径为r,则MO=DO-DM=r-1,
在Rt△AMO中,由勾股定理可知:AO =AM +MO ,代入数据:
,
解出:,
故圆⊙O的半径为4.
8.【答案】(1)证明:如图1,连结OC,
∵点O为直角三角形斜边AB的中点,
∴OC=OA=OB.
∴点C在⊙O上,
∵BD=OB,
∴AB=DO,
∵CD=CA,
∴∠A=∠D,
∴△ACB≌△DCO,
∴∠DCO=∠ACB=90°,
∴CD是⊙O的切线;
(2)解:如图2,
在Rt△ABC中,BC=ABsin∠A=2×8×sin30°=8,
∵∠ABC=90°-∠A=90°-30°=60°,
∴BE=BCcos60°=8× =4.
9.【答案】(1)证明:∵点D为△BCE的内心,
∴BD平分∠EBC.
∴∠EBD=∠CBD.
又∵∠DBE=∠BAD,
∴∠CBD=∠BAD.
又∵AB是圆的直径,
∴∠BDA=90°.
在Rt△BAD中,∠BAD+∠ABD=90°,
∴∠CBD+∠ABD=90°,即∠ABC=90°.
∴BC⊥AB.
又∵AB为直径,
∴BC是圆的切线;
(2)证明:连接ED,如图,则ED平分∠BEC,
∴∠BED=∠CED.
∵∠EFD为△BFD的外角
∴∠EFD=∠ADB+∠EBD=90°+∠EBD,
又∵四边形ABDG为圆的内接四边形,
∴∠EGD=180°﹣∠ABD=180°﹣(90°﹣∠CDB)=90°+∠CDB
又∵∠EBD=∠CBD,
∴∠EFD=∠EGD
又∵ED=ED,
∴△DFE≌△DGE(AAS ).
∴DF=DG.
10.【答案】(1)证明:连接 .
∵
∴
∵等腰三角形 的底角为30°,即
∴
∴ ∥
∵
∴ ,即 为⊙O的切线.
(2)解:连接 .
∵ ,
∴ ,即 是等边三角形,
∴ , ,
∵ ,
∴ ,
∴ ,
∴ .
11.【答案】(1)证明:∵,,
∴;
(2)证明:连接,
∵为的直径,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵是的半径,
∴是的切线;
(3)解:∵,,,
∴,
∵,
∴,
∵,
∴,,
∴.
∴的半径为.
12.【答案】(1)证明:连接OC,
∵ ,
∴ ,
∵ 平分 ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
又∵ 为 的半径,
∴ 为 的切线.
(2)解:连接OC,
∵ ,又 ,
∴四边形OABC是平行四边形,
∴ ,
∴ ,
∴ ,
又 是等边三角形,
∴ ,
∴ .
13.【答案】(1):证明:连接、、.
,,
,
,
,
,,
,
,
,
,,
,
,
,
,
,
是的切线.
(2)解:连接.由(1)可知:,
,
,
在中,,
,
,
,,
,
,
,
,
,
是的中点,
,
点是的中点,
,
是的直径,
,
在中,,,
,
,,
,
,即,
,
.
14.【答案】(1)证明:连接OD,
∴OD=OB
∴∠ODB=∠OBD.
∵AB是直径,
∴∠ADB=90°,
∴∠CDB=90°.
∵E为BC的中点,
∴DE=BE,
∴∠EDB=∠EBD,
∴∠ODB+∠EDB=∠OBD+∠EBD,
即∠EDO=∠EBO.
∵BC是以AB为直径的⊙O的切线,
∴AB⊥BC,
∴∠EBO=90°,
∴∠ODE=90°,
∴DE是⊙O的切线;
(2)解:∵S2=5S1,
∴S△ADB=2S△CDB,
∴ = ,
∵△BDC∽△ADB,
∴ = ,
∴DB2=AD DC,
∴ ,
∴tan∠BAC= ;
(3)解:∵tan∠BAC= ,
∴ ,得BC= AB=2 ,
∵E为BC的中点,
∴BE= BC= ,
∴AE= .
15.【答案】(1)解:补全图形如图所示,则直线PC即为所求;
(2)圆周角定理;切线的判定
16.【答案】(1)证明:连接OD,
如图
∵ ,
∴ ,
又∵ ,
∴ ,
,
∴ ,
∴ =
∴点E为弧BD的中点
(2)证明:∵在 与 中,
∴ ,
∴ ,
∴CD为⊙О的切线.
(3)解:∵ ,∴ .
设 ,则 ,
在 和 中,
由勾股定理得:
,
解得: .
∴
∴
同课章节目录
