2024年九年级中考数学知识点专项练习:一次函数存在性问题(无答案)
文档属性
| 名称 | 2024年九年级中考数学知识点专项练习:一次函数存在性问题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 402.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 20:28:32 | ||
图片预览


文档简介
2024年初中数学中考知识点专项练习:一次函数存在性问题
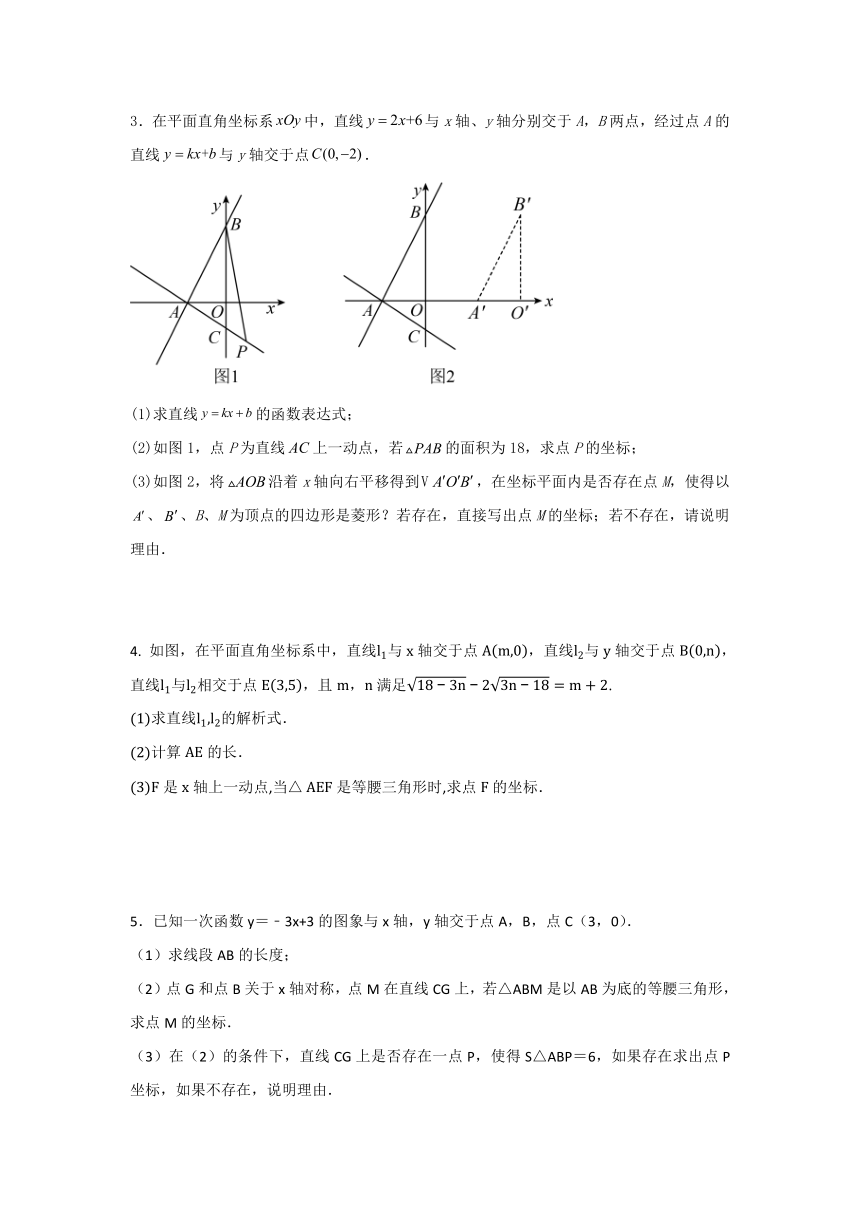
1.如图所示,直线与轴交于点,直线与轴交于点,直线与交于点.
(1)求点的坐标;
(2)点在直线上运动,求出满足条件且异于点的点的坐标;
(3)点为轴上一定点,当点在直线上运动时,请直接写出的最大值.
2.如图,平面直角坐标系中,直线AB:交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
(1)求直线AB的解析式和点B的坐标;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.
3.在平面直角坐标系中,直线与x轴、y轴分别交于A,B两点,经过点A的直线与y轴交于点.
(1)求直线的函数表达式;
(2)如图1,点P为直线上一动点,若的面积为18,求点P的坐标;
(3)如图2,将沿着x轴向右平移得到,在坐标平面内是否存在点M,使得以、、B、M为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
4. 如图,在平面直角坐标系中,直线与轴交于点,直线与轴交于点,直线与相交于点,且,满足.
求直线的解析式.
计算的长.
是轴上一动点,当是等腰三角形时,求点的坐标.
5.已知一次函数y=﹣3x+3的图象与x轴,y轴交于点A,B,点C(3,0).
(1)求线段AB的长度;
(2)点G和点B关于x轴对称,点M在直线CG上,若△ABM是以AB为底的等腰三角形,求点M的坐标.
(3)在(2)的条件下,直线CG上是否存在一点P,使得S△ABP=6,如果存在求出点P坐标,如果不存在,说明理由.
6.如图,过,两点的直线与直线交于点,平行于轴的直线从原点出发,以每秒1个单位长度的速度沿轴向左平移,到点时停止.直线分别交线段,于点,,以为边向右侧作等边.设与重叠部分图形的周长为,直线的运动时间为(秒.
(1)求点坐标;
(2)当点落在轴上时,求相应的时间的值;
(3)求与之间的关系式.【说明:不考虑直线平移过程中“起点”与“终点”时的情况.】
7.如图①,在四边形中,,点E是边上一点,,,连接,,可知,此时是等腰直角三角形;
【问题提出】
(1)如图②,在长方形中,点P是边上一点,在边上分别作出点E、F,使得点F、E、P是一个等腰直角三角形的三个顶点,且,
要求:用尺规作图,保留作图痕迹,不写作法;
【问题探究】
(2)如图③,在平面直角坐标系中,已知点,点,点C在第一象限内,若是等腰直角三角形,求点C的坐标;
【问题解决】
(3)如图④,在平面直角坐标系中,已知点,点C是y轴上的动点,是以点C为直角顶点的等腰直角三角形,连接,求的最小值.[注:在平面直角坐标系内,,,则]
8.如图,在平面直角坐标系中,为等腰直角三角形,,,点A的坐标为.
(1)求点B的坐标;
(2)在x轴上存在一点P,使得的和最小,求出这个最小值;
(3)在第四象限是否存在一点M,使得以点O,A,M为顶点的三角形是等腰直角三角形,若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
9.如图,在平面直角坐标系中,直线y=kx过点B(m,6),过点B分别作x轴和y轴的垂线,垂足分别为点A,C,∠AOB=30°.动点P从点O出发,以每秒2个单位长度的速度向点B运动,动点Q从点B出发.以每秒个单位长度的速度向点C运动.点P,Q同时开始运动,当点P到达点B时,点P,Q同时停止运动,设运动时间为t秒.
(1)求m与k的值;
(2)设△PQB的面积为S,求S与t的关系式;
(3)若以点P,Q,B为顶点的三角形是等腰三角形,请求出t的值.(温擎提示:在直角三角形中,30°的角所对的直角边等于斜边的一半)
10.如图,已知一次函数与正比例函数的图象交于点,且与轴交于点.
(1)直接写出点的坐标为 ;点的坐标为 ;
(2)过点作轴于点,过点作直线l∥y轴.动点从点出发,以每秒个单位长的速度,沿的路线向点运动;同时直线从点出发,以相同速度向左平移,在平移过程中,直线交轴于点,交线段或线段于点.当点到达点时,点和直线都停止运动.在运动过程中,设动点运动的时间为秒.
当为何值时,以、、为顶点的三角形的面积为;
是否存在以、、为顶点的三角形是等腰三角形 若存在,直接写出的值;若不存在,请说明理由.
11.如图1,在平面直角坐标系中,直线AB与轴交于点A,与轴交于点B,与直线OC:交于点C.
(1)若直线AB解析式为,
①求点C的坐标;
②求△OAC的面积.
(2)如图2,作的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
12.在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且OB=OA,直线l2:y=k2x+b经过点C(,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
(1)求直线l1的解析式;
(2)如图1,连接CB,当CD⊥AB时,求点D的坐标和△BCD的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
1.如图所示,直线与轴交于点,直线与轴交于点,直线与交于点.
(1)求点的坐标;
(2)点在直线上运动,求出满足条件且异于点的点的坐标;
(3)点为轴上一定点,当点在直线上运动时,请直接写出的最大值.
2.如图,平面直角坐标系中,直线AB:交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
(1)求直线AB的解析式和点B的坐标;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.
3.在平面直角坐标系中,直线与x轴、y轴分别交于A,B两点,经过点A的直线与y轴交于点.
(1)求直线的函数表达式;
(2)如图1,点P为直线上一动点,若的面积为18,求点P的坐标;
(3)如图2,将沿着x轴向右平移得到,在坐标平面内是否存在点M,使得以、、B、M为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
4. 如图,在平面直角坐标系中,直线与轴交于点,直线与轴交于点,直线与相交于点,且,满足.
求直线的解析式.
计算的长.
是轴上一动点,当是等腰三角形时,求点的坐标.
5.已知一次函数y=﹣3x+3的图象与x轴,y轴交于点A,B,点C(3,0).
(1)求线段AB的长度;
(2)点G和点B关于x轴对称,点M在直线CG上,若△ABM是以AB为底的等腰三角形,求点M的坐标.
(3)在(2)的条件下,直线CG上是否存在一点P,使得S△ABP=6,如果存在求出点P坐标,如果不存在,说明理由.
6.如图,过,两点的直线与直线交于点,平行于轴的直线从原点出发,以每秒1个单位长度的速度沿轴向左平移,到点时停止.直线分别交线段,于点,,以为边向右侧作等边.设与重叠部分图形的周长为,直线的运动时间为(秒.
(1)求点坐标;
(2)当点落在轴上时,求相应的时间的值;
(3)求与之间的关系式.【说明:不考虑直线平移过程中“起点”与“终点”时的情况.】
7.如图①,在四边形中,,点E是边上一点,,,连接,,可知,此时是等腰直角三角形;
【问题提出】
(1)如图②,在长方形中,点P是边上一点,在边上分别作出点E、F,使得点F、E、P是一个等腰直角三角形的三个顶点,且,
要求:用尺规作图,保留作图痕迹,不写作法;
【问题探究】
(2)如图③,在平面直角坐标系中,已知点,点,点C在第一象限内,若是等腰直角三角形,求点C的坐标;
【问题解决】
(3)如图④,在平面直角坐标系中,已知点,点C是y轴上的动点,是以点C为直角顶点的等腰直角三角形,连接,求的最小值.[注:在平面直角坐标系内,,,则]
8.如图,在平面直角坐标系中,为等腰直角三角形,,,点A的坐标为.
(1)求点B的坐标;
(2)在x轴上存在一点P,使得的和最小,求出这个最小值;
(3)在第四象限是否存在一点M,使得以点O,A,M为顶点的三角形是等腰直角三角形,若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
9.如图,在平面直角坐标系中,直线y=kx过点B(m,6),过点B分别作x轴和y轴的垂线,垂足分别为点A,C,∠AOB=30°.动点P从点O出发,以每秒2个单位长度的速度向点B运动,动点Q从点B出发.以每秒个单位长度的速度向点C运动.点P,Q同时开始运动,当点P到达点B时,点P,Q同时停止运动,设运动时间为t秒.
(1)求m与k的值;
(2)设△PQB的面积为S,求S与t的关系式;
(3)若以点P,Q,B为顶点的三角形是等腰三角形,请求出t的值.(温擎提示:在直角三角形中,30°的角所对的直角边等于斜边的一半)
10.如图,已知一次函数与正比例函数的图象交于点,且与轴交于点.
(1)直接写出点的坐标为 ;点的坐标为 ;
(2)过点作轴于点,过点作直线l∥y轴.动点从点出发,以每秒个单位长的速度,沿的路线向点运动;同时直线从点出发,以相同速度向左平移,在平移过程中,直线交轴于点,交线段或线段于点.当点到达点时,点和直线都停止运动.在运动过程中,设动点运动的时间为秒.
当为何值时,以、、为顶点的三角形的面积为;
是否存在以、、为顶点的三角形是等腰三角形 若存在,直接写出的值;若不存在,请说明理由.
11.如图1,在平面直角坐标系中,直线AB与轴交于点A,与轴交于点B,与直线OC:交于点C.
(1)若直线AB解析式为,
①求点C的坐标;
②求△OAC的面积.
(2)如图2,作的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
12.在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且OB=OA,直线l2:y=k2x+b经过点C(,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
(1)求直线l1的解析式;
(2)如图1,连接CB,当CD⊥AB时,求点D的坐标和△BCD的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
同课章节目录
