2024年九年级中考数学练习 一次函数(无答案)
文档属性
| 名称 | 2024年九年级中考数学练习 一次函数(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 19:10:47 | ||
图片预览


文档简介
①函数关系式
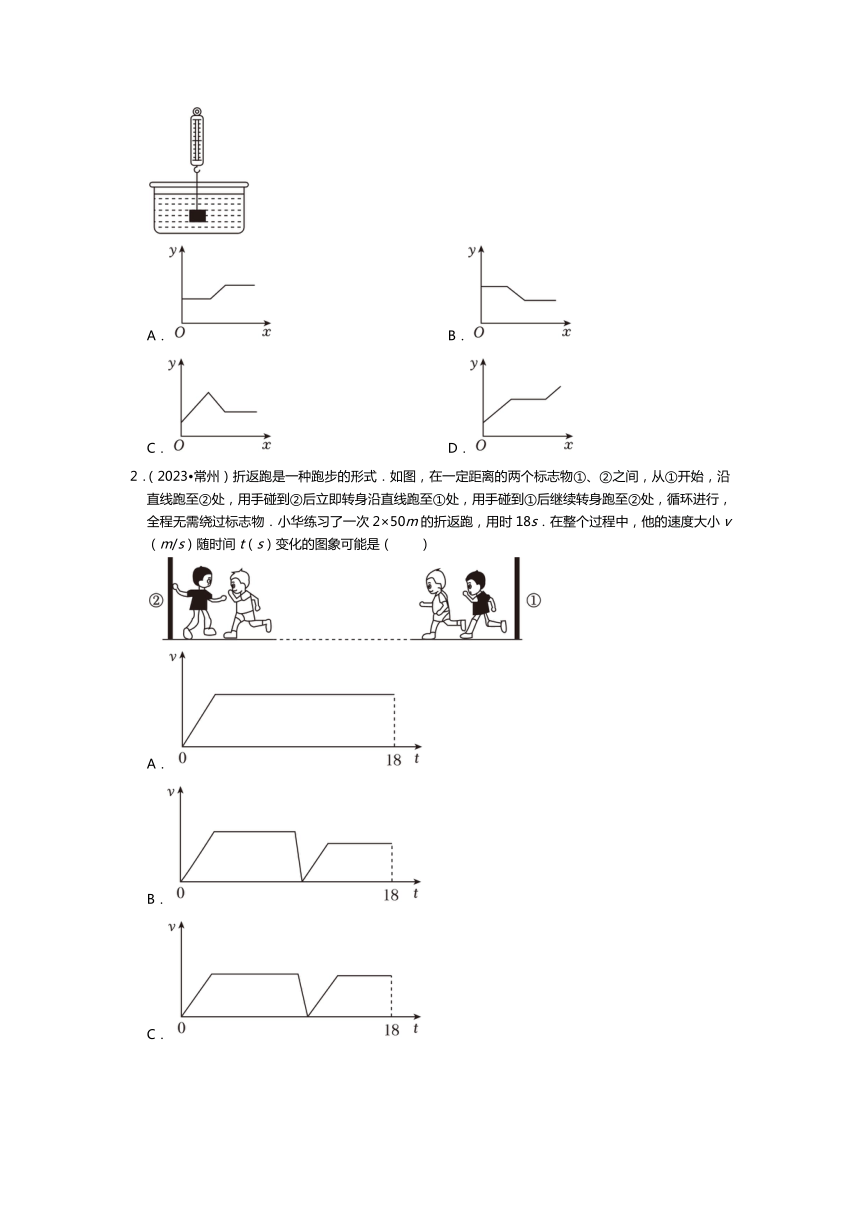
1.(2023春 道里区期末)如图所示的图象分别给出了x与y的对应关系,其中表示y是x的函数的是( )
A. B.
C. D.
2.(2023 鼓楼区校级模拟)观察表1和表2,下列判断正确的是( )
表1:
x ﹣2 1
y1 1 2 3 4
表2:
x ﹣2 2 ﹣1 1
y2 4 1
A.y1是x的函数,y2不是x的函数
B.y1和y2都是x的函数
C.y1不是x的函数,y2是x的函数
D.y1和y2都不是x的函数
3.(2023 海淀区校级三模)如图,有一个球形容器,小海在往容器里注水的过程中发现,水面的高度h、水面的面积S及注水量V是三个变量.下列有四种说法:
①S是V的函数;②V是S的函数;③h是S的函数,④S是h的函数.
其中所有正确结论的序号是( )
A.①③ B.①④ C.②③ D.②④
4.(2022 广东)水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为C=2πr.下列判断正确的是( )
A.2是变量 B.π是变量 C.r是变量 D.C是常量
5.(2023 南海区校级模拟)球的体积是V,球的半径为R,则V=πR3,其中变量和常量分别是( )
A.变量是V,R;常量是,π
B.变量是R,π;常量是
C.变量是V,R,π;常量是
D.变量是V,R3;常量是π
6.(2022 大连)汽车油箱中有汽油30L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,平均耗油量为0.1L/km.当0≤x≤300时,y与x的函数解析式是( )
A.y=0.1x B.y=﹣0.1x+30
C.y= D.y=﹣0.1x2+30x
7.(2022春 龙岗区期末)某人用新充值的50元IC卡打长途电话,按通话时间3分钟内收2.4元、超过1分钟加收1元钱的方式缴纳话费,若通话时间为t分钟(t≥3),则卡中所剩话费y与时间t之间的关系式是 .
②自变量取值范围
1.(2023 哈尔滨)在函数中,自变量x的取值范围是 .
2.(2023 黑龙江)在函数y=中,自变量x的取值范围是 .
3.(2023 黄石)函数的自变量x的取值范围是( )
A.x≥0 B.x≠1 C.x≥0且x≠1 D.x>1
4.(2022 丹东)在函数y=中,自变量x的取值范围是( )
A.x≥3 B.x≥﹣3 C.x≥3且x≠0 D.x≥﹣3且x≠0
5.(2022 恩施州)函数y=的自变量x的取值范围是( )
A.x≠3 B.x≥3 C.x≥﹣1且x≠3 D.x≥﹣1
6.(2023 齐齐哈尔)在函数 中,自变量x的取值范围是 .
③函数图像
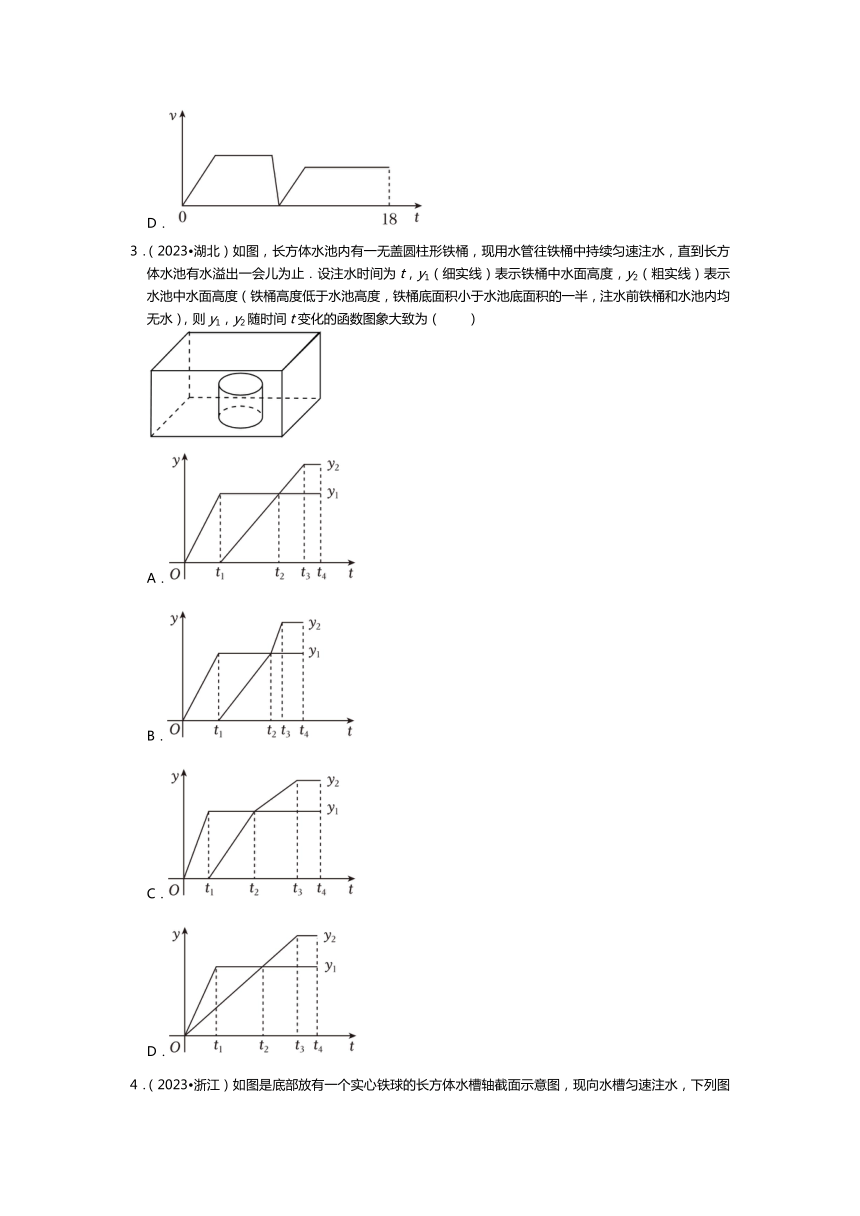
1.(2023 广安)如图,用弹簧测力计将一铁块悬于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度,则下列能反映弹簧测力计的读数y(单位:N)与铁块被提起的时间x(单位:s)之间的函数关系的大致图象是( )
A. B.
C. D.
2.(2023 常州)折返跑是一种跑步的形式.如图,在一定距离的两个标志物①、②之间,从①开始,沿直线跑至②处,用手碰到②后立即转身沿直线跑至①处,用手碰到①后继续转身跑至②处,循环进行,全程无需绕过标志物.小华练习了一次2×50m的折返跑,用时18s.在整个过程中,他的速度大小v(m/s)随时间t(s)变化的图象可能是( )
A.
B.
C.
D.
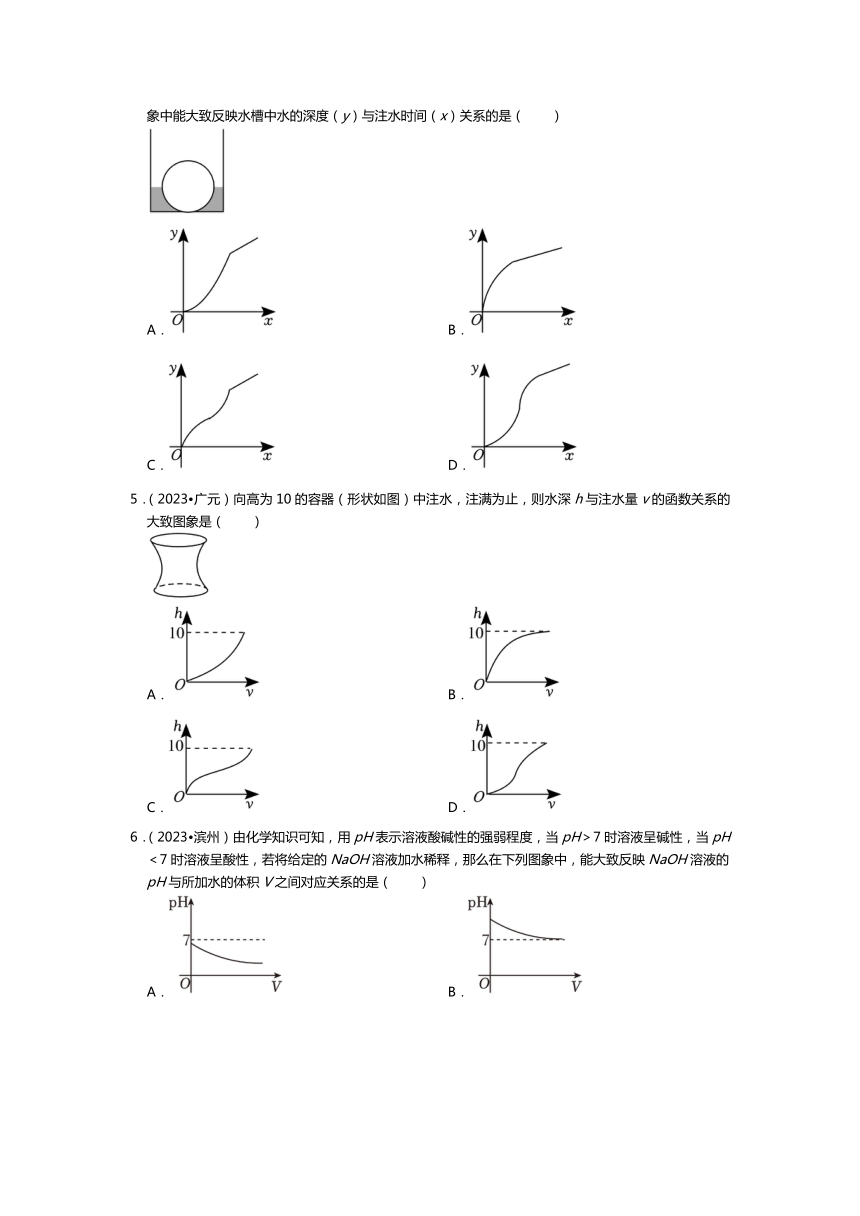
3.(2023 湖北)如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为t,y1(细实线)表示铁桶中水面高度,y2(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则y1,y2随时间t变化的函数图象大致为( )
A.
B.
C.
D.
4.(2023 浙江)如图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( )
A. B.
C. D.
5.(2023 广元)向高为10的容器(形状如图)中注水,注满为止,则水深h与注水量v的函数关系的大致图象是( )
A. B.
C. D.
6.(2023 滨州)由化学知识可知,用pH表示溶液酸碱性的强弱程度,当pH>7时溶液呈碱性,当pH<7时溶液呈酸性,若将给定的NaOH溶液加水稀释,那么在下列图象中,能大致反映NaOH溶液的pH与所加水的体积V之间对应关系的是( )
A. B.
C. D.
7.(2022 雅安)一辆公共汽车从车站开出,加速行驶一段后开始匀速行驶.过了一段时间,汽车到达下一个车站.乘客上、下车后汽车开始加速,一段时间后又开始匀速行驶.下面的哪一幅图可以近似地刻画出汽车在这段时间内的速度变化情况( )
A. B.
C. D.
8.(2022 台州)吴老师家、公园、学校依次在同一条直线上,家到公园、公园到学校的距离分别为400m,600m.他从家出发匀速步行8min到公园后,停留4min,然后匀速步行6min到学校.设吴老师离公园的距离为y(单位:m),所用时间为x(单位:min),则下列表示y与x之间函数关系的图象中,正确的是( )
A. B.
C. D.
9.(2022 遵义)遵义市某天的气温y1(单位:℃)随时间t(单位:h)的变化如图所示,设y2表示0时到t时气温的值的极差(即0时到t时范围气温的最大值与最小值的差),则y2与t的函数图象大致是( )
A. B.
C. D.
10.(2022 锦州)如图,在Rt△ABC中,∠ABC=90°,AB=2BC=4,动点P从点A出发,以每秒1个单位长度的速度沿线段AB匀速运动,当点P运动到点B时,停止运动,过点P作PQ⊥AB交AC于点Q,将△APQ沿直线PQ折叠得到△A′PQ,设动点P的运动时间为t秒,△A′PQ与△ABC重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
11.(2023 锦州)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,在△DEF中,DE=DF=5,EF=8,BC与EF在同一条直线上,点C与点E重合.△ABC以每秒1个单位长度的速度沿线段EF所在直线向右匀速运动,当点B运动到点F时,△ABC停止运动.设运动时间为t秒,△ABC与△DEF重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
12.(2022 鞍山)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4cm,CD⊥AB,垂足为点D,动点M从点A出发沿AB方向以cm/s的速度匀速运动到点B,同时动点N从点C出发沿射线DC方向以1cm/s的速度匀速运动.当点M停止运动时,点N也随之停止,连接MN.设运动时间为ts,△MND的面积为Scm2,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
13.(2023 鞍山)如图,在矩形ABCD中,对角线AC,BD交于点O,AB=4,,垂直于BC的直线MN从AB出发,沿BC方向以每秒个单位长度的速度平移,当直线MN与CD重合时停止运动,运动过程中MN分别交矩形的对角线AC,BD于点E,F,以EF为边在MN左侧作正方形EFGH,设正方形EFGH与△AOB重叠部分的面积为S,直线MN的运动时间为t s,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
14.(2022 西宁)如图,△ABC中,BC=6,BC边上的高为3,点D,E,F分别在边BC,AB,AC上,且EF∥BC.设点E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致是( )
A. B.
C. D.
15.(2022 潍坊)如图,在 ABCD中,∠A=60°,AB=2,AD=1,点E,F在 ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
A.B.
C. D.
16.(2022 衡阳)如图,在四边形ABCD中,∠B=90°,AC=6,AB∥CD,AC平分∠DAB.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
A. B.
C. D.
17.(2023 齐齐哈尔)如图,在正方形ABCD中,AB=4,动点M,N分别从点A,B同时出发,沿射线AB,射线BC的方向匀速运动,且速度的大小相等,连接DM,MN,ND.设点M
运动的路程为x(0≤x≤4),△DMN的面积为S,下列图象中能反映S与x之间函数关系的是( )
A. B.
C. D.
18.(2023 大庆)如图1,在平行四边形ABCD中,∠ABC=120°,已知点P在边AB上,以1m/s的速度从点A向点B运动,点Q在边BC上,以m/s的速度从点B向点C运动.若点P,Q同时出发,当点P到达点B时,点Q恰好到达点C处,此时两点都停止运动.图2是△BPQ的面积y(m2)与点P的运动时间t(s)之间的函数关系图象(点M为图象的最高点),则平行四边形ABCD的面积为( )
A.12m2 B.12m2 C.24m2 D.24m2
19.(2023 南通)如图1,△ABC中,∠C=90°,AC=15,BC=20.点D从点A出发沿折线A﹣C﹣B运动到点B停止,过点D作DE⊥AB,垂足为E.设点D运动的路径长为x,△BDE的面积为y,若y与x的对应关系如图2所示,则a﹣b的值为( )
A.54 B.52 C.50 D.48
20.(2023 金昌)如图1,正方形ABCD的边长为4,E为CD边的中点.动点P从点A出发沿AB→BC匀速运动,运动到点C时停止.设点P的运动路程为x,线段PE的长为y,y与x的函数图象如图2所示,则点M的坐标为( )
A.(4,2) B.(4,4) C.(4,2) D.(4,5)
21.(2023 河南)如图1,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为,图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为( )
A.6 B.3 C. D.
22.(2023 深圳)如图1,在Rt△ABC中,动点P从A点运动到B点再到C点后停止,速度为2单位/s,其中BP长与运动时间t(单位:s)的关系如图2,则AC的长为( )
A. B. C.17 D.5
④一次函数
(1)一次函数定义
1.(2020 青白江区模拟)下列函数关系式:(1)y=﹣x;(2)y=x﹣1;(3)y=;(4)y=x2,其中一次函数的个数是( )
A.1 B.2 C.3 D.4
2.(2022 郫都区模拟)若函数y=(m﹣1)x|m|+2是一次函数,则m的值为( )
A.1 B.﹣1 C.±1 D.2
3.(2020 阳谷县校级模拟)若y=(m﹣1)x2﹣|m|+3是关于x的一次函数,则m的值为( )
A.1 B.﹣1 C.±1 D.±2
4.(2022 铁西区二模)若y=x+2﹣3b是正比例函数,则b的值是( )
A.0 B.﹣ C. D.﹣
5.(2021 陕西模拟)若函数y=kxk﹣2是正比例函数,则k的值为( )
A.k=3 B.k≠0 C.k=3或1 D.k>3
6.(2017 北湖区校级模拟)若函数y=(2m+6)x2+(1﹣m)x是正比例函数,则m的值是( )
A.m=﹣3 B.m=1 C.m=3 D.m>﹣3
(2)一次函数性质
7.(2023 乐山)下列各点在函数y=2x﹣1图象上的是( )
A.(﹣1,3) B.(0,1) C.(1,﹣1) D.(2,3)
8.(2023 广西)函数y=kx+3的图象经过点(2,5),则k= .
9.(2022 株洲)在平面直角坐标系中,一次函数y=5x+1的图象与y轴的交点的坐标为( )
A.(0,﹣1) B.(﹣,0) C.(,0) D.(0,1)
10.(2023 南充)如图,直线y=kx﹣2k+3(k为常数,k<0)与x,y轴分别交于点A,B,则+的值是 .
11.(2014 铜仁地区)正比例函数y=2x的大致图象是( )
A. B. C. D.
12.(2023 沈阳)已知一次函数y=kx+b的图象如图所示,则k,b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
13.(2023 通辽)在平面直角坐标系中,一次函数y=2x﹣3的图象是( )
A. B.
C. D.
14.(2022 沈阳)在平面直角坐标系中,一次函数y=﹣x+1的图象是( )
A.B. C.D.
15.(2020 济南)若m<﹣2,则一次函数y=(m+1)x+1﹣m的图象可能是( )
A.B. C.D.
16.(2023 陕西)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
A.B.C.D.
17.(2022 辽宁)如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图象分别为直线l1和直线l2,下列结论正确的是( )
A.k1 k2<0 B.k1+k2<0 C.b1﹣b2<0 D.b1 b2<0
18.(2022 安徽)在同一平面直角坐标系中,一次函数y=ax+a2与y=a2x+a的图象可能是( )
A.B. C.D.
19.(2021 商河县校级模拟)一次函数y1=ax+b与一次函数y2=bx﹣a在同一平面直角坐标系中的图象大致是( )
A. B. C.D.
20.(2023 长沙)下列一次函数中,y随x的增大而减小的函数是( )
A.y=2x+1 B.y=x﹣4 C.y=2x D.y=﹣x+1
21.(2023 新疆)一次函数y=x+1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
22.(2023 金昌)若直线y=kx(k是常数,k≠0)经过第一、第三象限,则k的值可为( )
A.﹣2 B.﹣1 C.﹣ D.2
23.(2023 巴中)一次函数y=(k﹣3)x+2的函数值y随x增大而减小,则k的取值范围是( )
A.k>0 B.k<0 C.k>3 D.k<3
24.(2022 包头)在一次函数y=﹣5ax+b(a≠0)中,y的值随x值的增大而增大,且ab>0,则点A(a,b)在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
25.(2022 眉山)一次函数y=(2m﹣1)x+2的值随x的增大而增大,则点P(﹣m,m)所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
26.(2020 牡丹江)已知一次函数y=(2m﹣3)x+3n+1的图象经过一、二、三象限,则m、n的取值是( )
A.m>3,n>3 B.m>,n>﹣ C.m<,n< D.m>,n<
27.(2022秋 江北区校级期末)若一次函数y=(2﹣2k)x﹣k (k≠0)的函数值随x的增大而增大,且函数的图象不经过第二象限,则k的取值范围是( )
A.k<1 B.0<k<1 C.k>0 D.k>0或k<1
28.(2023 盘锦)关于x的一次函数y=(2a+1)x+a﹣2,若y随x的增大而增大,且图象与y轴的交点在原点下方,则实数a的取值范围是 .
29.(2022 兰州)若一次函数y=2x+1的图象经过点(﹣3,y1),(4,y2),则y1与y2的大小关系是( )
A.y1<y2 B.y1>y2 C.y1≤y2 D.y1≥y2
30.(2022 邵阳)在直角坐标系中,已知点A(,m),点B(,n)是直线y=kx+b(k<0)上的两点,则m,n的大小关系是( )
A.m<n B.m>n C.m≥n D.m≤n
31.(2022 盘锦)点A(x1,y1),B(x2,y2)在一次函数y=(a﹣2)x+1的图象上,当x1>x2时,y1<y2,则a的取值范围是 .
32.(2023春 芜湖期末)直线y=3x+b上有三个点(﹣2.3,y1),(﹣1.3,y2),(2.7,y3),则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2<y1<y3 C.y1<y2<y3 D.y2>y1>y3
33.(2022 绍兴)已知(x1,y1),(x2,y2),(x3,y3)为直线y=﹣2x+3上的三个点,且x1<x2<x3,则以下判断正确的是( )
A.若x1x2>0,则y1y3>0 B.若x1x3<0,则y1y2>0
C.若x2x3>0,则y1y3>0 D.若x2x3<0,则y1y2>0
34.(2023 盘锦)关于x的一次函数y=(2a+1)x+a﹣2,若y随x的增大而增大,且图象与y轴的交点在原点下方,则实数a的取值范围是 .
35.(2023 西湖区校级二模)若A(x1,y1),B(x2,y2) 分别在一次函数y=kx+b(k>0)图象上两个不相同的点,记P=(x1﹣x2)(y1﹣y2),则P为( )
A.0 B.正数 C.负数 1 D.非负数
36.(2023春 秦皇岛月考)若一次函数y=kx+b(k≠0)在﹣3≤x≤2的范围内y的最大值比最小值大5,则下列说法正确的是( )
A.k的值为1或﹣1
B.y随x的增大而减小
C.该函数的图象不可能经过第一、二、四象限
D.满足题意的函数表达式只有2个
37.(2021春 海珠区期末)已知一次函数y=mx﹣4m,当1≤x≤3时,2≤y≤6,则m的值为( )
A.3 B.2 C.﹣2 D.2或﹣2
(3)一次函数平移、对称
1.(2021 陕西)在平面直角坐标系中,将直线y=﹣2x向上平移3个单位,平移后的直线经过点(﹣1,m),则m的值为( )
A.﹣1 B.1 C.﹣5 D.5
2.(2023 无锡)将函数y=2x+1的图象向下平移2个单位长度,所得图象对应的函数表达式是( )
A.y=2x﹣1 B.y=2x+3 C.y=4x﹣3 D.y=4x+5
3.(2022 灞桥区校级模拟)将正比例函数y=x向上平移1个单位长度,则平移后的函数图象与一次函数y=﹣3x+m的图象的交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2021 陕西)在平面直角坐标系中,若将一次函数y=2x+m﹣1的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )
A.﹣5 B.5 C.﹣6 D.6
5.(2023 内蒙古)在平面直角坐标系中,将正比例函数y=﹣2x的图象向右平移3个单位长度得到一次函数y=kx+b(k≠0)的图象,则该一次函数的解析式为( )
A.y=﹣2x+3 B.y=﹣2x+6 C.y=﹣2x﹣3 D.y=﹣2x﹣6
6.(2018 娄底)将直线y=2x﹣3向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( )
A.y=2x﹣4 B.y=2x+4 C.y=2x+2 D.y=2x﹣2
7.(2022 陇县二模)把直线y=﹣x+4向下平移n个单位长度后,与直线y=2x﹣4的交点在第四象限,则n的取值范围是( )
A.2<n<8 B.4<n<6 C.n>8 D.n<6
8.(2023 鄂城区校级模拟)如图,A(1,0)、B(3,0)、M(4,3),动点P从点A出发,沿x轴以每秒1个单位长的速度向右移动,且过点P的直线y=﹣x+b也随之平移,设移动时间为t秒,若直线与线段BM有公共点,则t的取值范围为( )
A.3≤t≤7 B.3≤t≤6 C.2≤t≤6 D.2≤t≤5
9.(2023 包头模拟)在平面直角坐标系中,点A的坐标为(0,6)点B的坐标为(2,4),△OAB沿x轴向右平移后得到△EDF,点B的对应点F是直线y=x上的一点,则点A的对应点D点的坐标为 .
10.(2022 宁夏)如图,点B的坐标是(0,3),将△OAB沿x轴向右平移至△CDE,点B的对应点E恰好落在直线y=2x﹣3上,则点A移动的距离是 .
11.(2022 和平区三模)一次函数y=kx+b(k,b是常数,k≠0)和直线y=﹣2x平行,且经过点(2,﹣1),则b的值为 .
12.(2022 宁远县模拟)直线y=kx+x+b与y=3x﹣6平行,将该直线向下平移3个单位长度后经过点(3,﹣1)则该函数解析式为 .
13.(2022 雁塔区校级模拟)已知一次函数y=x﹣b的图象沿x轴翻折后经过点(4,1),则b的值为( )
A.﹣5 B.5 C.﹣3 D.3
14.(2021 桂林)如图,与图中直线y=﹣x+1关于x轴对称的直线的函数表达式是 .
15.(2022 雁塔区校级三模)一次函数y=﹣kx+3的图象关于x轴对称后经过(2,﹣1),则k的值是( )
A.1 B.﹣1 C.5 D.﹣5
16.(2022 碑林区校级一模)直线l1:y=mx+2与y轴交于点A,与x轴交于点B,直线l2与直线l1关于x轴对称且过点(2,﹣1),则△ABO的面积为( )
A.8 B.1 C.2 D.4
17.(2021 蒲城县二模)已知直线y=﹣x﹣2沿y轴向上平移m个单位后,所得直线与y=x+4关于y轴对称,则m的值为( )
A.3 B.4 C.5 D.6
18.(2022 武功县一模)已知直线y=2x+m与直线y=nx+4(n≠0)关于y轴对称,则直线y=mx+n与坐标轴围成的三角形的面积为( )
A. B.1 C. D.2
19.(2023 陕西)在平面直角坐标系中,直线y=﹣x+m(m为常数)与x轴交于点A,将该直线沿x轴向左平移6个单位长度后,与x轴交于点A′.若点A′与A关于原点O对称,则m的值为( )
A.﹣3 B.3 C.﹣6 D.6
20.(2020 碑林区校级模拟)若直线y=kx+3与直线y=2x+b关于直线x=1对称,则k、b值分别为( )
A.k=2、b=﹣3 B.k=﹣2、b=﹣3 C.k=﹣2、b=1 D.k=﹣2、b=﹣1
21.(2021 雁塔区校级模拟)在平面直角坐标系中,直线l1与l2关于直线y=1对称,若直线l1的表达式为y=﹣2x+3,则直线l2与y轴的交点坐标为( )
A.(0,) B.(0,) C.(0,0) D.(0,﹣1)
22.(2021 雁塔区校级模拟)已知直线l:y=2x+4,直线l1与直线l关于点M(1,0)对称,则直线l1的表达式为( )
A.y=﹣2x+4 B.y=2x﹣6 C.y=﹣2x﹣4 D.y=2x﹣8
23.(2020 南京)将一次函数y=﹣2x+4的图象绕原点O逆时针旋转90°,所得到的图象对应的函数表达式是 .
24.(2023 雅安)在平面直角坐标系中,将函数y=x的图象绕坐标原点逆时针旋转90°,再向上平移1个单位长度,所得直线的函数表达式为( )
A.y=﹣x+1 B.y=x+1 C.y=﹣x﹣1 D.y=x﹣1
25.(2023春 临邑县期末)如图所示,直线分别与x轴、y轴交于点A、B,以线段AB为边,在第二象限内作等腰直角△ABC,∠BAC=90°,则过B、C两点直线的解析式为 .
26.(2021春 未央区月考)如图,在平面直角坐标系xOy中,直线y=﹣x+3分别与x轴y轴交于点A和点B,将直线AB绕点A顺时针旋转90°后,所得直线与y轴的交点坐标为( )
A.(0,﹣1) B.(0,﹣) C.(0,﹣) D.(0,﹣)
27.(2022 碑林区校级二模)把一次函数y=x+1的图象绕点(2,0)顺时针旋转180°所得直线的表达式为( )
A.y=﹣x+2 B.y=﹣x+3 C.y=x﹣4 D.y=x﹣5
28.(2022 雁塔区校级三模)已知一次函数y=﹣x+2的图象,绕x轴上一点P(m,0)旋转180°,所得的图象经过(0.﹣1),则m的值为( )
A.﹣2 B.﹣1 C.1 D.2
29.(2022秋 太仓市期末)如图.直线l1:与x轴,y轴分别交于点A,B,直线l2经过点A,与y轴负半轴交于点C,且∠BAC=45°,则直线l2的函数表达式为 .
30.(2023秋 龙岗区期中)如图所示,直线分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )
A. B. C. D.
31.(2021秋 北碚区校级期末)如图,已知直线y=x+3交x轴于点B,交y轴于点A,点C在y轴负半轴上,∠ABC=45°,则直线BC的解析式为 .
32.(2023 东营)如图,一束光线从点A(﹣2,5)出发,经过y轴上的点B(0,1)反射后经过点C(m,n),则2m﹣n的值是 .
(4)一次函数与不等式
1.(2023 丹东)如图,直线y=ax+b(a≠0)过点A(0,3),B(4,0),则不等式ax+b>0的解集是( )
A.x>4 B.x<4 C.x>3 D.x<3
2.(2021 福建)如图,一次函数y=kx+b(k>0)的图象过点(﹣1,0),则不等式k(x﹣1)+b>0的解集是( )
A.x>﹣2 B.x>﹣1 C.x>0 D.x>1
3.(2020 湘潭)如图,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,则x的取值范围为( )
A.x≤1 B.x≥1 C.x<1 D.x>1
4.(2023春 佛山月考)已知一次函数y=kx+b(k>0)的图象过点(1,0),则不等式k(x+2)+b>0的解集是( )
A.x>﹣2 B.x>﹣1 C.x>0 D.x>1
5.(2022 南通)根据图象,可得关于x的不等式kx>﹣x+3的解集是( )
A.x<2 B.x>2 C.x<1 D.x>1
6.(2022 西宁)如图,直线y1=k1x与直线y2=k2x+b交于点A(1,2).当y1<y2时,x的取值范围是 .
7.(2019 烟台)如图,直线y=x+2与直线y=ax+c相交于点P(m,3),则关于x的不等式x+2≤ax+c的解集为 .
8.(2022 鄂州)数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,根据图象可知,x的取值范围是( )
A.x>3 B.x<3 C.x<1 D.x>1
9.(2021 娄底)如图,直线y=x+b和y=kx+4与x轴分别相交于点A(﹣4,0),点B(2,0),则解集为( )
A.﹣4<x<2 B.x<﹣4 C.x>2 D.x<﹣4或x>2
10.(2023春 渠县校级期中)观察图中的函数图象,则关于x的不等式(a﹣b)x>c的解集为( )
A.x<2 B.x<1 C.x>2 D.x>1
11.(2023 芝罘区一模)如图,函数y=﹣3x和y=kx+b的图象交于点A(m,4),则关于x的不等式kx+b+3x<0的解集为 .
12.(2023 富川县二模)如图,直线y1=mx,y2=kx+b交于点P(2,1),则关于x的不等式kx+b>mx>﹣1的解集为 .
12.(2023 薛城区一模)我们知道,若ab>0.则有或.如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( )
A.x>2 B.﹣0.5<x<2
C.0<x<2 D.x<﹣0.5或x>2
14.(2022 德阳)如图,已知点A(﹣2,3),B(2,1),直线y=kx+k经过点P(﹣1,0).试探究:直线与线段AB有交点时k的变化情况,猜想k的取值范围是 .
(5)一次函数与方程
1.(2021 辽宁)如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x= B.x=1 C.x=2 D.x=4
2.(2021 贺州)直线y=ax+b(a≠0)过点A(0,1),B(2,0),则关于x的方程ax+b=0的解为( )
A.x=0 B.x=1 C.x=2 D.x=3
3.(2022 市南区校级二模)若关于x的方程﹣2x+b=0的解为x=2,则直线y=﹣2x+b一定经过点( )
A.(2,0) B.(0,3) C.(4,0) D.(2,5)
4.(2022 陕西)在同一平面直角坐标系中,直线y=﹣x+4与y=2x+m相交于点P(3,n),则关于x,y的方程组的解为( )
A. B. C. D.
5.(2022 贵阳)在同一平面直角坐标系中,一次函数y=ax+b与y=mx+n(a<m<0)的图象如图所示.小星根据图象得到如下结论:
①在一次函数y=mx+n的图象中,y的值随着x值的增大而增大;
②方程组的解为;
③方程mx+n=0的解为x=2;
④当x=0时,ax+b=﹣1.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
6.(2022 梧州)如图,在平面直角坐标系中,直线y=2x+b与直线y=﹣3x+6相交于点A,则关于x,y的二元一次方程组的解是( )
A. B. C. D.
7.(2022 天心区校级三模)如图,在平面直角坐标系中,直线l1:y=x+4与直线l2:y=mx+n交于点A(﹣1,b),则关于x,y的方程组的解为( )
A. B. C. D.
8.(2019 贵阳)在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是 .
9.(2021 蕉岭县模拟)在平面直角坐标系中,一次函数y=mx+b(m,b均为常数)与正比例函数y=nx(n为常数)的图象如图所示,则关于x的方程mx=nx﹣b的解为( )
A.x=3 B.x=﹣3 C.x=1 D.x=﹣1
10.(2021 毕节市模拟)如图,直线y=ax+b与x轴交于A点(5,0),与直线y=mx交于B点(2,﹣k),则关于x的一元一次方程ax﹣b=mx的解为( )
A.x=﹣2 B.x=2 C.x=﹣5 D.x=5
11.(2021 高青县二模)若一次函数y=kx+3(k为常数且k≠0)的图象经过点(﹣2,0),则关于x的方程k(x﹣5)+3=0的解为( )
A.x=﹣5 B.x=﹣3 C.x=3 D.x=5
12.(2016 资阳)已知关于x的方程mx+3=4的解为x=1,则直线y=(m﹣2)x﹣3一定不经过第 象限.
13.(2021 仪征市校级模拟)若一次函数y=ax+b(a、b为常数,且a≠0)的图象过点(2,0),则关于x的方程a(x+1)+b=0的解是 .
14.(2021 乾县模拟)若x=2是关于x的方程mx+n=0(m≠0)的解,则一次函数y=﹣mx﹣n的图象与x轴的交点坐标是( )
A.(3,0) B.(0,3) C.(0,2) D.(2,0)
15.(2022 德阳)如图,已知点A(﹣2,3),B(2,1),直线y=kx+k经过点P(﹣1,0).试探究:直线与线段AB有交点时k的变化情况,猜想k的取值范围是 .
16.(2016 巴中)已知二元一次方程组的解为,则在同一平面直角坐标系中,直线l1:y=x+5与直线l2:y=﹣x﹣1的交点坐标为 .
17.(2022 柳州)如图,直线y1=x+3分别与x轴、y轴交于点A和点C,直线y2=﹣x+3分别与x轴、y轴交于点B和点C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
A.1 B.2 C.4 D.6
⑤一次函数应用
1.(2015 广安)某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了,如果加满汽油后汽车行驶的路程为xkm,油箱中剩油量为yL,则y与x之间的函数解析式和自变量取值范围分别是( )
A.y=0.12x,x>0 B.y=60﹣0.12x,x>0
C.y=0.12x,0≤x≤500 D.y=60﹣0.12x,0≤x≤500
2.(2013 潍坊模拟)油箱中有油300L,油从管道中匀速流出,1小时流完.油箱中剩余的油量Q(L)与油流出的时间t(s)之间的函数解析式和自变量t取值范围正确的是( )
A. B.
C. D.
3.(2023 山西)一种弹簧秤最大能称不超过10kg的物体,不挂物体时弹簧的长为12cm,每挂重1kg物体,弹簧伸长0.5cm,在弹性限度内,挂重后弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为( )
A.y=12﹣0.5x B.y=12+0.5x C.y=10+0.5x D.y=0.5x
4.(2022 呼和浩特)某超市糯米的价格为5元/千克,端午节推出促销活动:一次购买的数量不超过2千克时,按原价售出,超过2千克时,超过的部分打8折.若某人付款14元,则他购买了 千克糯米;设某人的付款金额为x元,购买量为y千克,则购买量y关于付款金额x(x>10)的函数解析式为 .
5.(2021 饶平县校级模拟)一个弹簧不挂重物时长10cm,挂上重物后伸长的长度与所挂重物的质量成正比,如果挂上1kg的物体后,弹簧伸长3cm,则弹簧总长y(单位:cm)关于所挂重物x(单位:kg)的函数关系式为 (不需要写出自变量取值范围)
6.(2023 郴州)第11届中国(湖南)矿物宝石国际博览会在我市举行,小方一家上午9:00开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.以下是他们家出发后离家的距离s与时间的函数图象.分析图中信息,下列说法正确的是( )
A.途中修车花了30min
B.修车之前的平均速度是500m/min
C.车修好后的平均速度是80m/min
D.车修好后的平均速度是修车之前的平均速度的1.5倍
7.(2022 桂林)桂林作为国际旅游名城,每年吸引着大量游客前来观光.现有一批游客分别乘坐甲乙两辆旅游大巴同时从旅行社前往某个旅游景点.行驶过程中甲大巴因故停留一段时间后继续驶向景点,乙大巴全程匀速驶向景点.两辆大巴的行程s(km)随时间t(h)变化的图象(全程)如图所示.依据图中信息,下列说法错误的是( )
A.甲大巴比乙大巴先到达景点
B.甲大巴中途停留了0.5h
C.甲大巴停留后用1.5h追上乙大巴
D.甲大巴停留前的平均速度是60km/h
8.(2022 玉林)龟兔赛跑之后,输了比赛的兔子决定和乌龟再赛一场.图中的函数图象表示了龟兔再次赛跑的过程(x表示兔子和乌龟从起点出发所走的时间,y1,y2分别表示兔子与乌龟所走的路程).下列说法错误的是( )
A.兔子和乌龟比赛路程是500米
B.中途,兔子比乌龟多休息了35分钟
C.兔子比乌龟多走了50米
D.比赛结果,兔子比乌龟早5分钟到达终点
9.(2023 随州)甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,关于下列结论:①A,B两城相距300km;②甲车的平均速度是60km/h,乙车的平均速度是100km/h;③乙车先出发,先到达B城;④甲车在9:30追上乙车.正确的有( )
A.①② B.①③ C.②④ D.①④
10.(2023 聊城)甲乙两地相距a千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离y(千米)与两人行驶时刻t(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为( )
A.8:28 B.8:30 C.8:32 D.8:35
11.(2023 朝阳)甲乙两人骑自行车分别从A,B两地同时出发相向而行,甲匀速骑行到B地,乙匀速骑行到A地,甲的速度大于乙的速度,两人分别到达目的地后停止骑行.两人之间的距离y(米)和骑行的时间x(秒)之间的函数关系图象如图所示,现给出下列结论:①a=450;②b=150;③甲的速度为10米/秒;④当甲、乙相距50米时,甲出发了55秒或65秒.其中正确的结论有( )
A.①② B.①③ C.②④ D.③④
12.(2022 绥化)小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A.2.7分钟 B.2.8分钟 C.3分钟 D.3.2分钟
13.(2022 阜新)快递员经常驾车往返于公司和客户之间.在快递员完成某次投递业务时,他与客户的距离s(km)与行驶时间t(h)之间的函数关系如图所示(因其他业务,曾在途中有一次折返,且快递员始终匀速行驶),那么快递员的行驶速度是 km/h.
14.(2022 苏州)一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量y(升)与时间x(分钟)之间的函数关系如图所示,则图中a的值为 .
1.(2023春 道里区期末)如图所示的图象分别给出了x与y的对应关系,其中表示y是x的函数的是( )
A. B.
C. D.
2.(2023 鼓楼区校级模拟)观察表1和表2,下列判断正确的是( )
表1:
x ﹣2 1
y1 1 2 3 4
表2:
x ﹣2 2 ﹣1 1
y2 4 1
A.y1是x的函数,y2不是x的函数
B.y1和y2都是x的函数
C.y1不是x的函数,y2是x的函数
D.y1和y2都不是x的函数
3.(2023 海淀区校级三模)如图,有一个球形容器,小海在往容器里注水的过程中发现,水面的高度h、水面的面积S及注水量V是三个变量.下列有四种说法:
①S是V的函数;②V是S的函数;③h是S的函数,④S是h的函数.
其中所有正确结论的序号是( )
A.①③ B.①④ C.②③ D.②④
4.(2022 广东)水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为C=2πr.下列判断正确的是( )
A.2是变量 B.π是变量 C.r是变量 D.C是常量
5.(2023 南海区校级模拟)球的体积是V,球的半径为R,则V=πR3,其中变量和常量分别是( )
A.变量是V,R;常量是,π
B.变量是R,π;常量是
C.变量是V,R,π;常量是
D.变量是V,R3;常量是π
6.(2022 大连)汽车油箱中有汽油30L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,平均耗油量为0.1L/km.当0≤x≤300时,y与x的函数解析式是( )
A.y=0.1x B.y=﹣0.1x+30
C.y= D.y=﹣0.1x2+30x
7.(2022春 龙岗区期末)某人用新充值的50元IC卡打长途电话,按通话时间3分钟内收2.4元、超过1分钟加收1元钱的方式缴纳话费,若通话时间为t分钟(t≥3),则卡中所剩话费y与时间t之间的关系式是 .
②自变量取值范围
1.(2023 哈尔滨)在函数中,自变量x的取值范围是 .
2.(2023 黑龙江)在函数y=中,自变量x的取值范围是 .
3.(2023 黄石)函数的自变量x的取值范围是( )
A.x≥0 B.x≠1 C.x≥0且x≠1 D.x>1
4.(2022 丹东)在函数y=中,自变量x的取值范围是( )
A.x≥3 B.x≥﹣3 C.x≥3且x≠0 D.x≥﹣3且x≠0
5.(2022 恩施州)函数y=的自变量x的取值范围是( )
A.x≠3 B.x≥3 C.x≥﹣1且x≠3 D.x≥﹣1
6.(2023 齐齐哈尔)在函数 中,自变量x的取值范围是 .
③函数图像
1.(2023 广安)如图,用弹簧测力计将一铁块悬于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度,则下列能反映弹簧测力计的读数y(单位:N)与铁块被提起的时间x(单位:s)之间的函数关系的大致图象是( )
A. B.
C. D.
2.(2023 常州)折返跑是一种跑步的形式.如图,在一定距离的两个标志物①、②之间,从①开始,沿直线跑至②处,用手碰到②后立即转身沿直线跑至①处,用手碰到①后继续转身跑至②处,循环进行,全程无需绕过标志物.小华练习了一次2×50m的折返跑,用时18s.在整个过程中,他的速度大小v(m/s)随时间t(s)变化的图象可能是( )
A.
B.
C.
D.
3.(2023 湖北)如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为t,y1(细实线)表示铁桶中水面高度,y2(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则y1,y2随时间t变化的函数图象大致为( )
A.
B.
C.
D.
4.(2023 浙江)如图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( )
A. B.
C. D.
5.(2023 广元)向高为10的容器(形状如图)中注水,注满为止,则水深h与注水量v的函数关系的大致图象是( )
A. B.
C. D.
6.(2023 滨州)由化学知识可知,用pH表示溶液酸碱性的强弱程度,当pH>7时溶液呈碱性,当pH<7时溶液呈酸性,若将给定的NaOH溶液加水稀释,那么在下列图象中,能大致反映NaOH溶液的pH与所加水的体积V之间对应关系的是( )
A. B.
C. D.
7.(2022 雅安)一辆公共汽车从车站开出,加速行驶一段后开始匀速行驶.过了一段时间,汽车到达下一个车站.乘客上、下车后汽车开始加速,一段时间后又开始匀速行驶.下面的哪一幅图可以近似地刻画出汽车在这段时间内的速度变化情况( )
A. B.
C. D.
8.(2022 台州)吴老师家、公园、学校依次在同一条直线上,家到公园、公园到学校的距离分别为400m,600m.他从家出发匀速步行8min到公园后,停留4min,然后匀速步行6min到学校.设吴老师离公园的距离为y(单位:m),所用时间为x(单位:min),则下列表示y与x之间函数关系的图象中,正确的是( )
A. B.
C. D.
9.(2022 遵义)遵义市某天的气温y1(单位:℃)随时间t(单位:h)的变化如图所示,设y2表示0时到t时气温的值的极差(即0时到t时范围气温的最大值与最小值的差),则y2与t的函数图象大致是( )
A. B.
C. D.
10.(2022 锦州)如图,在Rt△ABC中,∠ABC=90°,AB=2BC=4,动点P从点A出发,以每秒1个单位长度的速度沿线段AB匀速运动,当点P运动到点B时,停止运动,过点P作PQ⊥AB交AC于点Q,将△APQ沿直线PQ折叠得到△A′PQ,设动点P的运动时间为t秒,△A′PQ与△ABC重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
11.(2023 锦州)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,在△DEF中,DE=DF=5,EF=8,BC与EF在同一条直线上,点C与点E重合.△ABC以每秒1个单位长度的速度沿线段EF所在直线向右匀速运动,当点B运动到点F时,△ABC停止运动.设运动时间为t秒,△ABC与△DEF重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
12.(2022 鞍山)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4cm,CD⊥AB,垂足为点D,动点M从点A出发沿AB方向以cm/s的速度匀速运动到点B,同时动点N从点C出发沿射线DC方向以1cm/s的速度匀速运动.当点M停止运动时,点N也随之停止,连接MN.设运动时间为ts,△MND的面积为Scm2,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
13.(2023 鞍山)如图,在矩形ABCD中,对角线AC,BD交于点O,AB=4,,垂直于BC的直线MN从AB出发,沿BC方向以每秒个单位长度的速度平移,当直线MN与CD重合时停止运动,运动过程中MN分别交矩形的对角线AC,BD于点E,F,以EF为边在MN左侧作正方形EFGH,设正方形EFGH与△AOB重叠部分的面积为S,直线MN的运动时间为t s,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
14.(2022 西宁)如图,△ABC中,BC=6,BC边上的高为3,点D,E,F分别在边BC,AB,AC上,且EF∥BC.设点E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致是( )
A. B.
C. D.
15.(2022 潍坊)如图,在 ABCD中,∠A=60°,AB=2,AD=1,点E,F在 ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
A.B.
C. D.
16.(2022 衡阳)如图,在四边形ABCD中,∠B=90°,AC=6,AB∥CD,AC平分∠DAB.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
A. B.
C. D.
17.(2023 齐齐哈尔)如图,在正方形ABCD中,AB=4,动点M,N分别从点A,B同时出发,沿射线AB,射线BC的方向匀速运动,且速度的大小相等,连接DM,MN,ND.设点M
运动的路程为x(0≤x≤4),△DMN的面积为S,下列图象中能反映S与x之间函数关系的是( )
A. B.
C. D.
18.(2023 大庆)如图1,在平行四边形ABCD中,∠ABC=120°,已知点P在边AB上,以1m/s的速度从点A向点B运动,点Q在边BC上,以m/s的速度从点B向点C运动.若点P,Q同时出发,当点P到达点B时,点Q恰好到达点C处,此时两点都停止运动.图2是△BPQ的面积y(m2)与点P的运动时间t(s)之间的函数关系图象(点M为图象的最高点),则平行四边形ABCD的面积为( )
A.12m2 B.12m2 C.24m2 D.24m2
19.(2023 南通)如图1,△ABC中,∠C=90°,AC=15,BC=20.点D从点A出发沿折线A﹣C﹣B运动到点B停止,过点D作DE⊥AB,垂足为E.设点D运动的路径长为x,△BDE的面积为y,若y与x的对应关系如图2所示,则a﹣b的值为( )
A.54 B.52 C.50 D.48
20.(2023 金昌)如图1,正方形ABCD的边长为4,E为CD边的中点.动点P从点A出发沿AB→BC匀速运动,运动到点C时停止.设点P的运动路程为x,线段PE的长为y,y与x的函数图象如图2所示,则点M的坐标为( )
A.(4,2) B.(4,4) C.(4,2) D.(4,5)
21.(2023 河南)如图1,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为,图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为( )
A.6 B.3 C. D.
22.(2023 深圳)如图1,在Rt△ABC中,动点P从A点运动到B点再到C点后停止,速度为2单位/s,其中BP长与运动时间t(单位:s)的关系如图2,则AC的长为( )
A. B. C.17 D.5
④一次函数
(1)一次函数定义
1.(2020 青白江区模拟)下列函数关系式:(1)y=﹣x;(2)y=x﹣1;(3)y=;(4)y=x2,其中一次函数的个数是( )
A.1 B.2 C.3 D.4
2.(2022 郫都区模拟)若函数y=(m﹣1)x|m|+2是一次函数,则m的值为( )
A.1 B.﹣1 C.±1 D.2
3.(2020 阳谷县校级模拟)若y=(m﹣1)x2﹣|m|+3是关于x的一次函数,则m的值为( )
A.1 B.﹣1 C.±1 D.±2
4.(2022 铁西区二模)若y=x+2﹣3b是正比例函数,则b的值是( )
A.0 B.﹣ C. D.﹣
5.(2021 陕西模拟)若函数y=kxk﹣2是正比例函数,则k的值为( )
A.k=3 B.k≠0 C.k=3或1 D.k>3
6.(2017 北湖区校级模拟)若函数y=(2m+6)x2+(1﹣m)x是正比例函数,则m的值是( )
A.m=﹣3 B.m=1 C.m=3 D.m>﹣3
(2)一次函数性质
7.(2023 乐山)下列各点在函数y=2x﹣1图象上的是( )
A.(﹣1,3) B.(0,1) C.(1,﹣1) D.(2,3)
8.(2023 广西)函数y=kx+3的图象经过点(2,5),则k= .
9.(2022 株洲)在平面直角坐标系中,一次函数y=5x+1的图象与y轴的交点的坐标为( )
A.(0,﹣1) B.(﹣,0) C.(,0) D.(0,1)
10.(2023 南充)如图,直线y=kx﹣2k+3(k为常数,k<0)与x,y轴分别交于点A,B,则+的值是 .
11.(2014 铜仁地区)正比例函数y=2x的大致图象是( )
A. B. C. D.
12.(2023 沈阳)已知一次函数y=kx+b的图象如图所示,则k,b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
13.(2023 通辽)在平面直角坐标系中,一次函数y=2x﹣3的图象是( )
A. B.
C. D.
14.(2022 沈阳)在平面直角坐标系中,一次函数y=﹣x+1的图象是( )
A.B. C.D.
15.(2020 济南)若m<﹣2,则一次函数y=(m+1)x+1﹣m的图象可能是( )
A.B. C.D.
16.(2023 陕西)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
A.B.C.D.
17.(2022 辽宁)如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图象分别为直线l1和直线l2,下列结论正确的是( )
A.k1 k2<0 B.k1+k2<0 C.b1﹣b2<0 D.b1 b2<0
18.(2022 安徽)在同一平面直角坐标系中,一次函数y=ax+a2与y=a2x+a的图象可能是( )
A.B. C.D.
19.(2021 商河县校级模拟)一次函数y1=ax+b与一次函数y2=bx﹣a在同一平面直角坐标系中的图象大致是( )
A. B. C.D.
20.(2023 长沙)下列一次函数中,y随x的增大而减小的函数是( )
A.y=2x+1 B.y=x﹣4 C.y=2x D.y=﹣x+1
21.(2023 新疆)一次函数y=x+1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
22.(2023 金昌)若直线y=kx(k是常数,k≠0)经过第一、第三象限,则k的值可为( )
A.﹣2 B.﹣1 C.﹣ D.2
23.(2023 巴中)一次函数y=(k﹣3)x+2的函数值y随x增大而减小,则k的取值范围是( )
A.k>0 B.k<0 C.k>3 D.k<3
24.(2022 包头)在一次函数y=﹣5ax+b(a≠0)中,y的值随x值的增大而增大,且ab>0,则点A(a,b)在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
25.(2022 眉山)一次函数y=(2m﹣1)x+2的值随x的增大而增大,则点P(﹣m,m)所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
26.(2020 牡丹江)已知一次函数y=(2m﹣3)x+3n+1的图象经过一、二、三象限,则m、n的取值是( )
A.m>3,n>3 B.m>,n>﹣ C.m<,n< D.m>,n<
27.(2022秋 江北区校级期末)若一次函数y=(2﹣2k)x﹣k (k≠0)的函数值随x的增大而增大,且函数的图象不经过第二象限,则k的取值范围是( )
A.k<1 B.0<k<1 C.k>0 D.k>0或k<1
28.(2023 盘锦)关于x的一次函数y=(2a+1)x+a﹣2,若y随x的增大而增大,且图象与y轴的交点在原点下方,则实数a的取值范围是 .
29.(2022 兰州)若一次函数y=2x+1的图象经过点(﹣3,y1),(4,y2),则y1与y2的大小关系是( )
A.y1<y2 B.y1>y2 C.y1≤y2 D.y1≥y2
30.(2022 邵阳)在直角坐标系中,已知点A(,m),点B(,n)是直线y=kx+b(k<0)上的两点,则m,n的大小关系是( )
A.m<n B.m>n C.m≥n D.m≤n
31.(2022 盘锦)点A(x1,y1),B(x2,y2)在一次函数y=(a﹣2)x+1的图象上,当x1>x2时,y1<y2,则a的取值范围是 .
32.(2023春 芜湖期末)直线y=3x+b上有三个点(﹣2.3,y1),(﹣1.3,y2),(2.7,y3),则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2<y1<y3 C.y1<y2<y3 D.y2>y1>y3
33.(2022 绍兴)已知(x1,y1),(x2,y2),(x3,y3)为直线y=﹣2x+3上的三个点,且x1<x2<x3,则以下判断正确的是( )
A.若x1x2>0,则y1y3>0 B.若x1x3<0,则y1y2>0
C.若x2x3>0,则y1y3>0 D.若x2x3<0,则y1y2>0
34.(2023 盘锦)关于x的一次函数y=(2a+1)x+a﹣2,若y随x的增大而增大,且图象与y轴的交点在原点下方,则实数a的取值范围是 .
35.(2023 西湖区校级二模)若A(x1,y1),B(x2,y2) 分别在一次函数y=kx+b(k>0)图象上两个不相同的点,记P=(x1﹣x2)(y1﹣y2),则P为( )
A.0 B.正数 C.负数 1 D.非负数
36.(2023春 秦皇岛月考)若一次函数y=kx+b(k≠0)在﹣3≤x≤2的范围内y的最大值比最小值大5,则下列说法正确的是( )
A.k的值为1或﹣1
B.y随x的增大而减小
C.该函数的图象不可能经过第一、二、四象限
D.满足题意的函数表达式只有2个
37.(2021春 海珠区期末)已知一次函数y=mx﹣4m,当1≤x≤3时,2≤y≤6,则m的值为( )
A.3 B.2 C.﹣2 D.2或﹣2
(3)一次函数平移、对称
1.(2021 陕西)在平面直角坐标系中,将直线y=﹣2x向上平移3个单位,平移后的直线经过点(﹣1,m),则m的值为( )
A.﹣1 B.1 C.﹣5 D.5
2.(2023 无锡)将函数y=2x+1的图象向下平移2个单位长度,所得图象对应的函数表达式是( )
A.y=2x﹣1 B.y=2x+3 C.y=4x﹣3 D.y=4x+5
3.(2022 灞桥区校级模拟)将正比例函数y=x向上平移1个单位长度,则平移后的函数图象与一次函数y=﹣3x+m的图象的交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2021 陕西)在平面直角坐标系中,若将一次函数y=2x+m﹣1的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )
A.﹣5 B.5 C.﹣6 D.6
5.(2023 内蒙古)在平面直角坐标系中,将正比例函数y=﹣2x的图象向右平移3个单位长度得到一次函数y=kx+b(k≠0)的图象,则该一次函数的解析式为( )
A.y=﹣2x+3 B.y=﹣2x+6 C.y=﹣2x﹣3 D.y=﹣2x﹣6
6.(2018 娄底)将直线y=2x﹣3向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( )
A.y=2x﹣4 B.y=2x+4 C.y=2x+2 D.y=2x﹣2
7.(2022 陇县二模)把直线y=﹣x+4向下平移n个单位长度后,与直线y=2x﹣4的交点在第四象限,则n的取值范围是( )
A.2<n<8 B.4<n<6 C.n>8 D.n<6
8.(2023 鄂城区校级模拟)如图,A(1,0)、B(3,0)、M(4,3),动点P从点A出发,沿x轴以每秒1个单位长的速度向右移动,且过点P的直线y=﹣x+b也随之平移,设移动时间为t秒,若直线与线段BM有公共点,则t的取值范围为( )
A.3≤t≤7 B.3≤t≤6 C.2≤t≤6 D.2≤t≤5
9.(2023 包头模拟)在平面直角坐标系中,点A的坐标为(0,6)点B的坐标为(2,4),△OAB沿x轴向右平移后得到△EDF,点B的对应点F是直线y=x上的一点,则点A的对应点D点的坐标为 .
10.(2022 宁夏)如图,点B的坐标是(0,3),将△OAB沿x轴向右平移至△CDE,点B的对应点E恰好落在直线y=2x﹣3上,则点A移动的距离是 .
11.(2022 和平区三模)一次函数y=kx+b(k,b是常数,k≠0)和直线y=﹣2x平行,且经过点(2,﹣1),则b的值为 .
12.(2022 宁远县模拟)直线y=kx+x+b与y=3x﹣6平行,将该直线向下平移3个单位长度后经过点(3,﹣1)则该函数解析式为 .
13.(2022 雁塔区校级模拟)已知一次函数y=x﹣b的图象沿x轴翻折后经过点(4,1),则b的值为( )
A.﹣5 B.5 C.﹣3 D.3
14.(2021 桂林)如图,与图中直线y=﹣x+1关于x轴对称的直线的函数表达式是 .
15.(2022 雁塔区校级三模)一次函数y=﹣kx+3的图象关于x轴对称后经过(2,﹣1),则k的值是( )
A.1 B.﹣1 C.5 D.﹣5
16.(2022 碑林区校级一模)直线l1:y=mx+2与y轴交于点A,与x轴交于点B,直线l2与直线l1关于x轴对称且过点(2,﹣1),则△ABO的面积为( )
A.8 B.1 C.2 D.4
17.(2021 蒲城县二模)已知直线y=﹣x﹣2沿y轴向上平移m个单位后,所得直线与y=x+4关于y轴对称,则m的值为( )
A.3 B.4 C.5 D.6
18.(2022 武功县一模)已知直线y=2x+m与直线y=nx+4(n≠0)关于y轴对称,则直线y=mx+n与坐标轴围成的三角形的面积为( )
A. B.1 C. D.2
19.(2023 陕西)在平面直角坐标系中,直线y=﹣x+m(m为常数)与x轴交于点A,将该直线沿x轴向左平移6个单位长度后,与x轴交于点A′.若点A′与A关于原点O对称,则m的值为( )
A.﹣3 B.3 C.﹣6 D.6
20.(2020 碑林区校级模拟)若直线y=kx+3与直线y=2x+b关于直线x=1对称,则k、b值分别为( )
A.k=2、b=﹣3 B.k=﹣2、b=﹣3 C.k=﹣2、b=1 D.k=﹣2、b=﹣1
21.(2021 雁塔区校级模拟)在平面直角坐标系中,直线l1与l2关于直线y=1对称,若直线l1的表达式为y=﹣2x+3,则直线l2与y轴的交点坐标为( )
A.(0,) B.(0,) C.(0,0) D.(0,﹣1)
22.(2021 雁塔区校级模拟)已知直线l:y=2x+4,直线l1与直线l关于点M(1,0)对称,则直线l1的表达式为( )
A.y=﹣2x+4 B.y=2x﹣6 C.y=﹣2x﹣4 D.y=2x﹣8
23.(2020 南京)将一次函数y=﹣2x+4的图象绕原点O逆时针旋转90°,所得到的图象对应的函数表达式是 .
24.(2023 雅安)在平面直角坐标系中,将函数y=x的图象绕坐标原点逆时针旋转90°,再向上平移1个单位长度,所得直线的函数表达式为( )
A.y=﹣x+1 B.y=x+1 C.y=﹣x﹣1 D.y=x﹣1
25.(2023春 临邑县期末)如图所示,直线分别与x轴、y轴交于点A、B,以线段AB为边,在第二象限内作等腰直角△ABC,∠BAC=90°,则过B、C两点直线的解析式为 .
26.(2021春 未央区月考)如图,在平面直角坐标系xOy中,直线y=﹣x+3分别与x轴y轴交于点A和点B,将直线AB绕点A顺时针旋转90°后,所得直线与y轴的交点坐标为( )
A.(0,﹣1) B.(0,﹣) C.(0,﹣) D.(0,﹣)
27.(2022 碑林区校级二模)把一次函数y=x+1的图象绕点(2,0)顺时针旋转180°所得直线的表达式为( )
A.y=﹣x+2 B.y=﹣x+3 C.y=x﹣4 D.y=x﹣5
28.(2022 雁塔区校级三模)已知一次函数y=﹣x+2的图象,绕x轴上一点P(m,0)旋转180°,所得的图象经过(0.﹣1),则m的值为( )
A.﹣2 B.﹣1 C.1 D.2
29.(2022秋 太仓市期末)如图.直线l1:与x轴,y轴分别交于点A,B,直线l2经过点A,与y轴负半轴交于点C,且∠BAC=45°,则直线l2的函数表达式为 .
30.(2023秋 龙岗区期中)如图所示,直线分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )
A. B. C. D.
31.(2021秋 北碚区校级期末)如图,已知直线y=x+3交x轴于点B,交y轴于点A,点C在y轴负半轴上,∠ABC=45°,则直线BC的解析式为 .
32.(2023 东营)如图,一束光线从点A(﹣2,5)出发,经过y轴上的点B(0,1)反射后经过点C(m,n),则2m﹣n的值是 .
(4)一次函数与不等式
1.(2023 丹东)如图,直线y=ax+b(a≠0)过点A(0,3),B(4,0),则不等式ax+b>0的解集是( )
A.x>4 B.x<4 C.x>3 D.x<3
2.(2021 福建)如图,一次函数y=kx+b(k>0)的图象过点(﹣1,0),则不等式k(x﹣1)+b>0的解集是( )
A.x>﹣2 B.x>﹣1 C.x>0 D.x>1
3.(2020 湘潭)如图,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,则x的取值范围为( )
A.x≤1 B.x≥1 C.x<1 D.x>1
4.(2023春 佛山月考)已知一次函数y=kx+b(k>0)的图象过点(1,0),则不等式k(x+2)+b>0的解集是( )
A.x>﹣2 B.x>﹣1 C.x>0 D.x>1
5.(2022 南通)根据图象,可得关于x的不等式kx>﹣x+3的解集是( )
A.x<2 B.x>2 C.x<1 D.x>1
6.(2022 西宁)如图,直线y1=k1x与直线y2=k2x+b交于点A(1,2).当y1<y2时,x的取值范围是 .
7.(2019 烟台)如图,直线y=x+2与直线y=ax+c相交于点P(m,3),则关于x的不等式x+2≤ax+c的解集为 .
8.(2022 鄂州)数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,根据图象可知,x的取值范围是( )
A.x>3 B.x<3 C.x<1 D.x>1
9.(2021 娄底)如图,直线y=x+b和y=kx+4与x轴分别相交于点A(﹣4,0),点B(2,0),则解集为( )
A.﹣4<x<2 B.x<﹣4 C.x>2 D.x<﹣4或x>2
10.(2023春 渠县校级期中)观察图中的函数图象,则关于x的不等式(a﹣b)x>c的解集为( )
A.x<2 B.x<1 C.x>2 D.x>1
11.(2023 芝罘区一模)如图,函数y=﹣3x和y=kx+b的图象交于点A(m,4),则关于x的不等式kx+b+3x<0的解集为 .
12.(2023 富川县二模)如图,直线y1=mx,y2=kx+b交于点P(2,1),则关于x的不等式kx+b>mx>﹣1的解集为 .
12.(2023 薛城区一模)我们知道,若ab>0.则有或.如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( )
A.x>2 B.﹣0.5<x<2
C.0<x<2 D.x<﹣0.5或x>2
14.(2022 德阳)如图,已知点A(﹣2,3),B(2,1),直线y=kx+k经过点P(﹣1,0).试探究:直线与线段AB有交点时k的变化情况,猜想k的取值范围是 .
(5)一次函数与方程
1.(2021 辽宁)如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x= B.x=1 C.x=2 D.x=4
2.(2021 贺州)直线y=ax+b(a≠0)过点A(0,1),B(2,0),则关于x的方程ax+b=0的解为( )
A.x=0 B.x=1 C.x=2 D.x=3
3.(2022 市南区校级二模)若关于x的方程﹣2x+b=0的解为x=2,则直线y=﹣2x+b一定经过点( )
A.(2,0) B.(0,3) C.(4,0) D.(2,5)
4.(2022 陕西)在同一平面直角坐标系中,直线y=﹣x+4与y=2x+m相交于点P(3,n),则关于x,y的方程组的解为( )
A. B. C. D.
5.(2022 贵阳)在同一平面直角坐标系中,一次函数y=ax+b与y=mx+n(a<m<0)的图象如图所示.小星根据图象得到如下结论:
①在一次函数y=mx+n的图象中,y的值随着x值的增大而增大;
②方程组的解为;
③方程mx+n=0的解为x=2;
④当x=0时,ax+b=﹣1.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
6.(2022 梧州)如图,在平面直角坐标系中,直线y=2x+b与直线y=﹣3x+6相交于点A,则关于x,y的二元一次方程组的解是( )
A. B. C. D.
7.(2022 天心区校级三模)如图,在平面直角坐标系中,直线l1:y=x+4与直线l2:y=mx+n交于点A(﹣1,b),则关于x,y的方程组的解为( )
A. B. C. D.
8.(2019 贵阳)在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是 .
9.(2021 蕉岭县模拟)在平面直角坐标系中,一次函数y=mx+b(m,b均为常数)与正比例函数y=nx(n为常数)的图象如图所示,则关于x的方程mx=nx﹣b的解为( )
A.x=3 B.x=﹣3 C.x=1 D.x=﹣1
10.(2021 毕节市模拟)如图,直线y=ax+b与x轴交于A点(5,0),与直线y=mx交于B点(2,﹣k),则关于x的一元一次方程ax﹣b=mx的解为( )
A.x=﹣2 B.x=2 C.x=﹣5 D.x=5
11.(2021 高青县二模)若一次函数y=kx+3(k为常数且k≠0)的图象经过点(﹣2,0),则关于x的方程k(x﹣5)+3=0的解为( )
A.x=﹣5 B.x=﹣3 C.x=3 D.x=5
12.(2016 资阳)已知关于x的方程mx+3=4的解为x=1,则直线y=(m﹣2)x﹣3一定不经过第 象限.
13.(2021 仪征市校级模拟)若一次函数y=ax+b(a、b为常数,且a≠0)的图象过点(2,0),则关于x的方程a(x+1)+b=0的解是 .
14.(2021 乾县模拟)若x=2是关于x的方程mx+n=0(m≠0)的解,则一次函数y=﹣mx﹣n的图象与x轴的交点坐标是( )
A.(3,0) B.(0,3) C.(0,2) D.(2,0)
15.(2022 德阳)如图,已知点A(﹣2,3),B(2,1),直线y=kx+k经过点P(﹣1,0).试探究:直线与线段AB有交点时k的变化情况,猜想k的取值范围是 .
16.(2016 巴中)已知二元一次方程组的解为,则在同一平面直角坐标系中,直线l1:y=x+5与直线l2:y=﹣x﹣1的交点坐标为 .
17.(2022 柳州)如图,直线y1=x+3分别与x轴、y轴交于点A和点C,直线y2=﹣x+3分别与x轴、y轴交于点B和点C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
A.1 B.2 C.4 D.6
⑤一次函数应用
1.(2015 广安)某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了,如果加满汽油后汽车行驶的路程为xkm,油箱中剩油量为yL,则y与x之间的函数解析式和自变量取值范围分别是( )
A.y=0.12x,x>0 B.y=60﹣0.12x,x>0
C.y=0.12x,0≤x≤500 D.y=60﹣0.12x,0≤x≤500
2.(2013 潍坊模拟)油箱中有油300L,油从管道中匀速流出,1小时流完.油箱中剩余的油量Q(L)与油流出的时间t(s)之间的函数解析式和自变量t取值范围正确的是( )
A. B.
C. D.
3.(2023 山西)一种弹簧秤最大能称不超过10kg的物体,不挂物体时弹簧的长为12cm,每挂重1kg物体,弹簧伸长0.5cm,在弹性限度内,挂重后弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为( )
A.y=12﹣0.5x B.y=12+0.5x C.y=10+0.5x D.y=0.5x
4.(2022 呼和浩特)某超市糯米的价格为5元/千克,端午节推出促销活动:一次购买的数量不超过2千克时,按原价售出,超过2千克时,超过的部分打8折.若某人付款14元,则他购买了 千克糯米;设某人的付款金额为x元,购买量为y千克,则购买量y关于付款金额x(x>10)的函数解析式为 .
5.(2021 饶平县校级模拟)一个弹簧不挂重物时长10cm,挂上重物后伸长的长度与所挂重物的质量成正比,如果挂上1kg的物体后,弹簧伸长3cm,则弹簧总长y(单位:cm)关于所挂重物x(单位:kg)的函数关系式为 (不需要写出自变量取值范围)
6.(2023 郴州)第11届中国(湖南)矿物宝石国际博览会在我市举行,小方一家上午9:00开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.以下是他们家出发后离家的距离s与时间的函数图象.分析图中信息,下列说法正确的是( )
A.途中修车花了30min
B.修车之前的平均速度是500m/min
C.车修好后的平均速度是80m/min
D.车修好后的平均速度是修车之前的平均速度的1.5倍
7.(2022 桂林)桂林作为国际旅游名城,每年吸引着大量游客前来观光.现有一批游客分别乘坐甲乙两辆旅游大巴同时从旅行社前往某个旅游景点.行驶过程中甲大巴因故停留一段时间后继续驶向景点,乙大巴全程匀速驶向景点.两辆大巴的行程s(km)随时间t(h)变化的图象(全程)如图所示.依据图中信息,下列说法错误的是( )
A.甲大巴比乙大巴先到达景点
B.甲大巴中途停留了0.5h
C.甲大巴停留后用1.5h追上乙大巴
D.甲大巴停留前的平均速度是60km/h
8.(2022 玉林)龟兔赛跑之后,输了比赛的兔子决定和乌龟再赛一场.图中的函数图象表示了龟兔再次赛跑的过程(x表示兔子和乌龟从起点出发所走的时间,y1,y2分别表示兔子与乌龟所走的路程).下列说法错误的是( )
A.兔子和乌龟比赛路程是500米
B.中途,兔子比乌龟多休息了35分钟
C.兔子比乌龟多走了50米
D.比赛结果,兔子比乌龟早5分钟到达终点
9.(2023 随州)甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,关于下列结论:①A,B两城相距300km;②甲车的平均速度是60km/h,乙车的平均速度是100km/h;③乙车先出发,先到达B城;④甲车在9:30追上乙车.正确的有( )
A.①② B.①③ C.②④ D.①④
10.(2023 聊城)甲乙两地相距a千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离y(千米)与两人行驶时刻t(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为( )
A.8:28 B.8:30 C.8:32 D.8:35
11.(2023 朝阳)甲乙两人骑自行车分别从A,B两地同时出发相向而行,甲匀速骑行到B地,乙匀速骑行到A地,甲的速度大于乙的速度,两人分别到达目的地后停止骑行.两人之间的距离y(米)和骑行的时间x(秒)之间的函数关系图象如图所示,现给出下列结论:①a=450;②b=150;③甲的速度为10米/秒;④当甲、乙相距50米时,甲出发了55秒或65秒.其中正确的结论有( )
A.①② B.①③ C.②④ D.③④
12.(2022 绥化)小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A.2.7分钟 B.2.8分钟 C.3分钟 D.3.2分钟
13.(2022 阜新)快递员经常驾车往返于公司和客户之间.在快递员完成某次投递业务时,他与客户的距离s(km)与行驶时间t(h)之间的函数关系如图所示(因其他业务,曾在途中有一次折返,且快递员始终匀速行驶),那么快递员的行驶速度是 km/h.
14.(2022 苏州)一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量y(升)与时间x(分钟)之间的函数关系如图所示,则图中a的值为 .
同课章节目录
