2024年九年级中考数学一轮复习-四边形 (无答案)
文档属性
| 名称 | 2024年九年级中考数学一轮复习-四边形 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 20:30:41 | ||
图片预览



文档简介
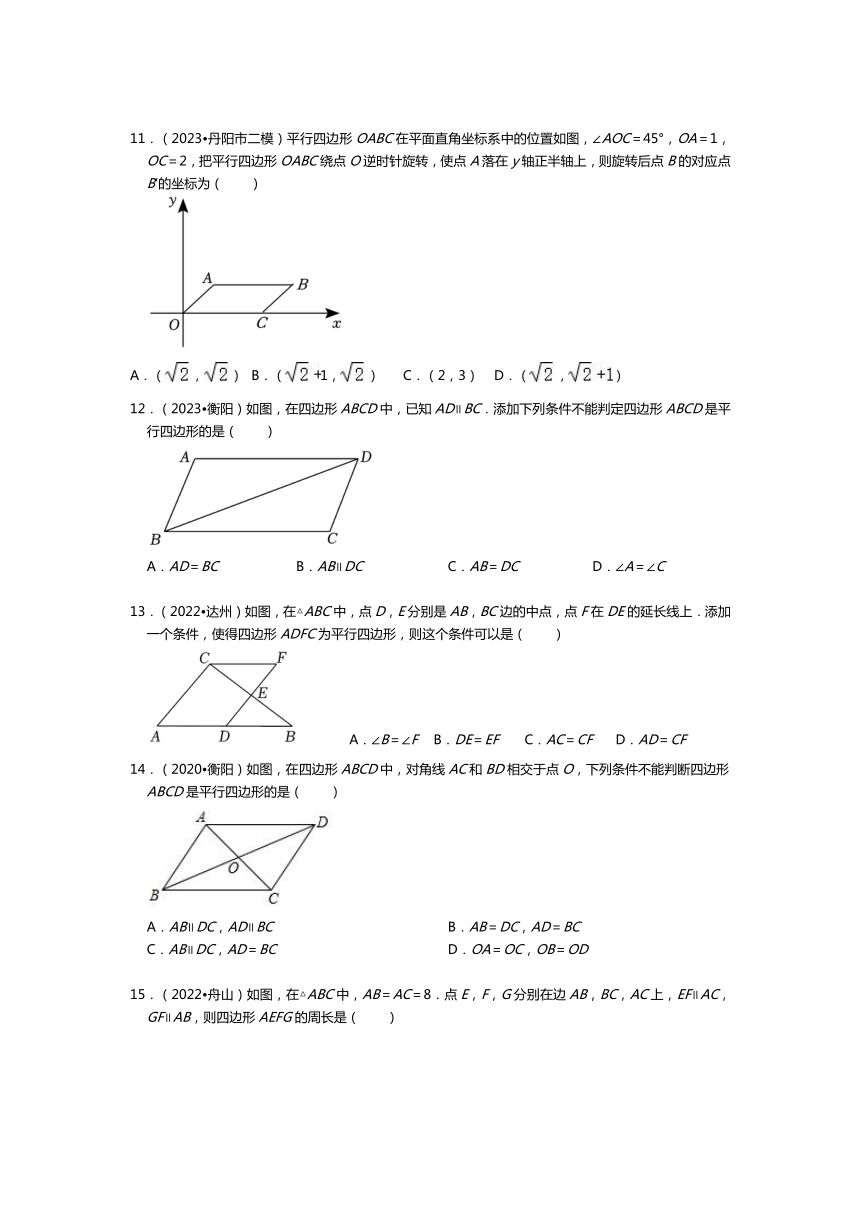
四边形
一、平行四边形
笔记:
1.定义:两组对边分别平行的四边形叫做平行四边形.
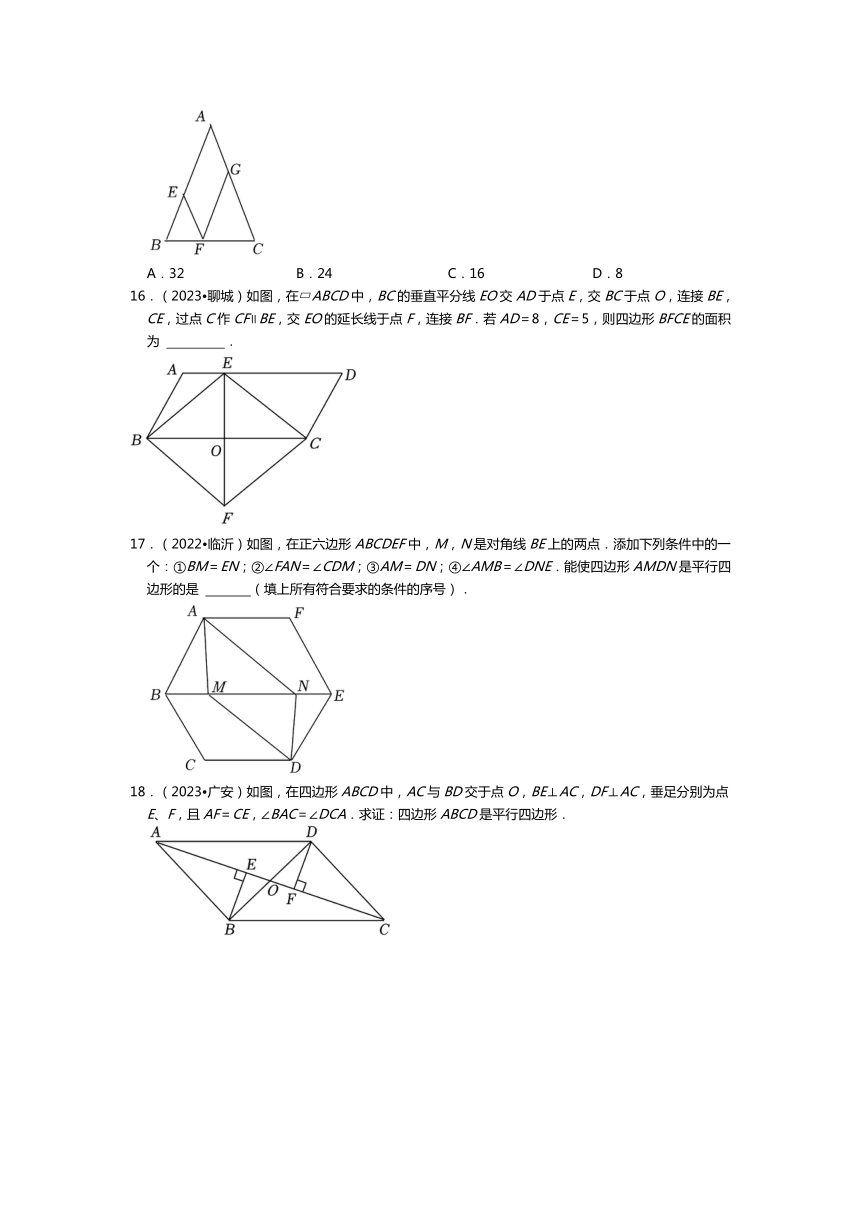
2.性质:(1)对边平行且相等;(2)对角相等;邻角互补;(3)对角线互相平分;(4)中心对称图形.
3.面积:
4.判定:(1)边:两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形.
(2)角:两组对角分别相等的四边形是平行四边形;任意两组邻角分别互补的四边形是平行四边形.
(3)边与角:一组对边平行,一组对角相等的四边形是平行四边形;
(4)对角线:对角线互相平分的四边形是平行四边形.
5.平行线的性质:(1)平行线间的距离都相等;(2)等底等高的平行四边形面积相等.
例题:
①平行四边形性质判定
1.(2023 益阳)如图, ABCD的对角线AC,BD交于点O,下列结论一定成立的是( )
A.OA=OB B.OA⊥OB C.OA=OC D.∠OBA=∠OBC
2.(2023 成都)如图,在 ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.AC=BD B.OA=OC C.AC⊥BD D.∠ADC=∠BCD
3.(2023 通辽)如图,用平移方法说明平行四边形的面积公式S=ah时,若△ABE平移到△DCF,a=4,h=3,则△ABE的平移距离为( )
A.3 B.4 C.5 D.12
4.(2022 益阳)如图,在 ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于点F,则BF的长为( )
A.5 B.4 C.3 D.2
5.(2020·湖南益阳)如图,的对角线,交于点,若,,则的长可能是( )
A. B. C. D.
6.(2022·广东广州)如图,在□ABCD中,AD=10,对角线AC 与BD相交于点O,AC+BD=22,则△BOC的周长为________
7.(2022·四川内江)如图,在 ABCD中,已知AB=12,AD=8,∠ABC的平分线BM交CD边于点M,则DM的长为( )
A.2 B.4 C.6 D.8
8.(2023 兰州)如图,在 ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE= °.
9.(2023 福建)如图,在 ABCD中,O为BD的中点,EF过点O且分别交AB,CD于点E,F.若AE=10,则CF的长为 .
10.(2023 凉山州)如图, ABCO的顶点O、A、C的坐标分别是(0,0)、(3,0)、(1,2).则顶点B的坐标是 .
11.(2023 丹阳市二模)平行四边形OABC在平面直角坐标系中的位置如图,∠AOC=45°,OA=1,OC=2,把平行四边形OABC绕点O逆时针旋转,使点A落在y轴正半轴上,则旋转后点B的对应点B′的坐标为( )
A.(,) B.(1,) C.(2,3) D.(,)
12.(2023 衡阳)如图,在四边形ABCD中,已知AD∥BC.添加下列条件不能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AB∥DC C.AB=DC D.∠A=∠C
13.(2022 达州)如图,在△ABC中,点D,E分别是AB,BC边的中点,点F在DE的延长线上.添加一个条件,使得四边形ADFC为平行四边形,则这个条件可以是( )
A.∠B=∠F B.DE=EF C.AC=CF D.AD=CF
14.(2020 衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
15.(2022 舟山)如图,在△ABC中,AB=AC=8.点E,F,G分别在边AB,BC,AC上,EF∥AC,GF∥AB,则四边形AEFG的周长是( )
A.32 B.24 C.16 D.8
16.(2023 聊城)如图,在 ABCD中,BC的垂直平分线EO交AD于点E,交BC于点O,连接BE,CE,过点C作CF∥BE,交EO的延长线于点F,连接BF.若AD=8,CE=5,则四边形BFCE的面积为 .
17.(2022 临沂)如图,在正六边形ABCDEF中,M,N是对角线BE上的两点.添加下列条件中的一个:①BM=EN;②∠FAN=∠CDM;③AM=DN;④∠AMB=∠DNE.能使四边形AMDN是平行四边形的是 (填上所有符合要求的条件的序号).
18.(2023 广安)如图,在四边形ABCD中,AC与BD交于点O,BE⊥AC,DF⊥AC,垂足分别为点E、F,且AF=CE,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.
19.(2023 杭州)如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形.
(2)若△ABE的面积等于2,求△CFO的面积.
20.(2023 扬州)如图,点E、F、G、H分别是平行四边形ABCD各边的中点,连接AF、CE相交于点M,连接AG、CH相交于点N.
(1)求证:四边形AMCN是平行四边形;
(2)若 AMCN的面积为4,求 ABCD的面积.
21.(2022 温州)如图,在△ABC中,AD⊥BC于点D,E,F分别是AC,AB的中点,O是DF的中点,EO的延长线交线段BD于点G,连结DE,EF,FG.
(1)求证:四边形DEFG是平行四边形.
(2)当AD=5,tan∠EDC=时,求FG的长.
22.(2021 北京)如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE∥DC,EF⊥AB,垂足为F.
(1)求证:四边形AECD是平行四边形;
(2)若AE平分∠BAC,BE=5,cosB=,求BF和AD的长.
②中位线
1.(2023 云南)如图,A、B两点被池塘隔开,A、B、C三点不共线.设AC、BC的中点分别为M、N.若MN=3米,则AB=( )
A.4米 B.6米 C.8米 D.10米
2.(2022 眉山)在△ABC中,AB=4,BC=6,AC=8,点D,E,F分别为边AB,AC,BC的中点,则△DEF的周长为( )
A.9 B.12 C.14 D.16
3.(2022·浙江丽水)如图,在中,D,E,F分别是,,的中点.若,,则四边形的周长是( )
A.28 B.14 C.10 D.7
4.(2022·江苏扬州)“做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片,第1次折叠使点落在边上的点处,折痕交于点;第2次折叠使点落在点处,折痕交于点.若,则_____________.
5.(2022 镇江)如图,在△ABC和△ABD中,∠ACB=∠ADB=90°,E、F、G分别为AB、AC、BC的中点,若DE=1,则FG= .
6.(2023 武功县模拟)如图,在Rt△ABC中,∠BAC=90°,AD是△ABC的中线,点E,F分别是AD,AC的中点,连接EF,若EF=3,则AD的长为 .
7.(2020·贵州毕节)如图,在矩形中,对角线,相交于点,点,分别是,的中点,连接,若,,则的长是( )
A. B. C. D.
8.(2022·黑龙江哈尔滨)如图,菱形的对角线相交于点O,点E在上,连接,点F为的中点,连接,若,,,则线段的长为___________.
9.(2022·广东广州)如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A. B.C. D.
10.(2022·浙江宁波)如图,在中,D为斜边的中点,E为上一点,F为中点.若,,则的长为( )
A. B.3 C. D.4
11.(2022 安顺)如图,在△ABC中,AC=2,∠ACB=120°,D是边AB的中点,E是边BC上一点,若DE平分△ABC的周长,则DE的长为( )
A. B. C. D.
12.(2023 铜仁市模拟)已知,Rt△ABC中,∠ABC=90°,AB=3,AD平分∠BAC,AD⊥BD,垂足为D,E为BC中点,连结DE,DE=1,则AD的值为( )
A. B. C. D.
13.(2023 广州)如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点M是边AC上一动点,点D,E分别是AB,MB的中点,当AM=2.4时,DE的长是 .若点N在边BC上,且CN=AM,点F,G分别是MN,AN的中点,当AM>2.4时,四边形DEFG面积S的取值范围是 .
二、矩形
笔记:
1.定义:有一个角是直角的平行四边形叫做矩形.
2.性质:(1)具有平行四边形的所有性质;(2)四个角都是直角;
(3)对角线互相平分且相等;(4)中心对称图形,轴对称图形.
3.面积:
4.判定:(1) 有一个角是直角的平行四边形是矩形.
(2)对角线相等的平行四边形是矩形.
(3)有三个角是直角的四边形是矩形.
5.由矩形得直角三角形的性质:
(1)直角三角形斜边上的中线等于斜边的一半;
(2)直角三角形中,30度角所对应的直角边等于斜边的一半.
例题:
①矩形判定、性质
1.(2023 襄阳)如图,矩形ABCD的对角线相交于点O,下列结论一定正确的是( )
A.AC平分∠BAD B.AB=BC
C.AC=BD D.AC⊥BD
2.(2023 呼和浩特)如图,矩形ABCD中,对角线BD的垂直平分线MN分别交AD,BC于点M,N.若AM=1,BN=2,则BD的长为( )
A. B.3 C. D.
3.(2022·青海)如图矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=3,BC=4,则图中阴影部分的面积为_____.
4.(2020·青海)如图,在矩形中,对角线,相交于点,已知,,则的长为________cm.
5.(2023 杭州)如图,矩形ABCD的对角线AC,BD相交于点O.若∠AOB=60°,则=( )
A. B. C. D.
6.(2021·辽宁鞍山)如图,矩形ABCD中,,对角线AC,BD交于点O,,垂足为点H,若,则AD的长为_______________.
7.(2022·四川达州)如图,点E在矩形的边上,将沿翻折,点A恰好落在边上的点F处,若,,则的长为( )
A.9 B.12 C.15 D.18
8.(2023 南通)如图,四边形ABCD是矩形,分别以点B,D为圆心,线段BC,DC长为半径画弧,两弧相交于点E,连接BE,DE,BD.若AB=4,BC=8,则∠ABE的正切值为( )
A. B. C. D.
9.(2023 台州)如图,矩形ABCD中,AB=4,AD=6.在边AD上取一点E,使BE=BC,过点C作CF⊥BE,垂足为点F,则BF的长为 .
10.(2023 苏州)如图,在平面直角坐标系中,点A的坐标为(9,0),点C的坐标为(0,3),以OA,OC为边作矩形OABC.动点E,F分别从点O,B同时出发,以每秒1个单位长度的速度沿OA,BC向终点A,C移动.当移动时间为4秒时,AC EF的值为( )
A. B.9 C.15 D.30
11.(2023 贵州)如图,在矩形ABCD中,点E为矩形内一点,且AB=1,AD=,∠BAE=75°,∠BCE=60°,则四边形ABCE的面积是 .
12.(2023 河南)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为 .
13.(2023 哈尔滨)矩形ABCD的对角线AC,BD相交于点O,点F在矩形ABCD边上,连接OF.若∠ADB=38°,∠BOF=30°,则∠AOF= .
14.(2022 陕西)在下列条件中,能够判定 ABCD为矩形的是( )
A.AB=AD B.AC⊥BD C.AB=AC D.AC=BD
15.(2020·湖北)已知中,下列条件:①;②;③;④平分,其中能说明是矩形的是( )
A.① B.② C.③ D.④
16.(2023 上海)在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD为矩形的是( )
A.AB∥CD B.AD=BC C.∠A=∠B D.∠A=∠D
17.(2023 大庆)如图,在平行四边形ABCD中,E为线段CD的中点,连接AC,AE,延长AE,BC交于点F,连接DF,∠ACF=90°.
(1)求证:四边形ACFD是矩形;
(2)若CD=13,CF=5,求四边形ABCE的面积.
18.(2023 北京)如图,在 ABCD中,点E,F分别在BC,AD上,BE=DF,AC=EF.
(1)求证:四边形AECF是矩形;
(2)若AE=BE,AB=2,tan∠ACB=,求BC的长.
19.(2023 温州)如图,已知矩形ABCD,点E在CB延长线上,点F在BC延长线上,过点F作FH⊥EF交ED的延长线于点H,连结AF交EH于点G,GE=GH.
(1)求证:BE=CF;
(2)当=,AD=4时,求EF的长.
20.(2022 十堰)如图, ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
(1)求证:BE=DF;
(2)设=k,当k为何值时,四边形DEBF是矩形?请说明理由.
②斜边中线
1.(2023 株洲)一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,点D为边AB的中点,点A、B对应的刻度为1、7,则CD=( )
A.3.5cm B.3cm C.4.5cm D.6cm
2.(2022 永州)如图,在Rt△ABC中,∠ABC=90°,∠C=60°,点D为边AC的中点,BD=2,则BC的长为( )
A. B.2 C.2 D.4
3.(2018 贺州)如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,AD=ED=3,则BC的长为( )
A.3 B.3 C.6 D.6
4.(2023 荆州)如图,CD为Rt△ABC斜边AB上的中线,E为AC的中点.若AC=8,CD=5,则DE= .
5.(2019 陕西)如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为( )
A.19° B.33° C.34° D.43°
6.(2022 雁塔区校级模拟)如图,在△ABC中,∠ACB=90°,∠A=22.5°,CD⊥AB于点D,点E为AB的中点,连接CE,若CD=2,则AB的长为( )
A.4 B.2 C.4 D.6
7.(2022 荆州)如图,在Rt△ABC中,∠ACB=90°,通过尺规作图得到的直线MN分别交AB,AC于D,E,连接CD.若CE=AE=1,则CD= .
8.(2023 雁塔区校级模拟)如图,△ABC中,∠ACB=90°,点E为AB的中点,点D在BC上,且AD=BD,AD、CE相交于点F,若∠B=20°,则∠DFE等于( )
A.70° B.60° C.50° D.40°
9.(2023 长安区校级二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,CD是△ABC的中线,E是CD的中点,连接AE,BE,若AE⊥BE,垂足为E,则AC的长为 .
10.(2021 蜀山区模拟)如图,△ABC中,∠C=90°,AC=10,BC=8,线段DE的两个端点D、E分别在边AC,BC上滑动,且DE=6,若点M、N分别是DE、AB的中点,则MN的最小值为( )
A.10﹣ B.﹣3 C.2﹣6 D.3
11.(2022 杭州)如图,在Rt△ACB中,∠ACB=90°,点M为边AB的中点,点E在线段AM上,EF⊥AC于点F,连接CM,CE.已知∠A=50°,∠ACE=30°.
(1)求证:CE=CM.
(2)若AB=4,求线段FC的长.
三、菱形
笔记:
1. 定义:有一组邻边相等的平行四边形叫做菱形.
2.性质:(1)具有平行四边形的一切性质;
(2)四条边相等;
(3)两条对角线互相平分且垂直,并且每一条对角线平分一组对角;
(4)中心对称图形,轴对称图形.
3.面积:
4.判定:(1)一组邻边相等的平行四边形是菱形;
(2)对角线互相垂直的平行四边形是菱形;
(3)四边相等的四边形是菱形.
例题:
1.(2021·广西柳州)如图,在菱形中,对角线,则的面积为( )
A.9 B.10 C.11 D.12
2.(2022·甘肃兰州)如图,菱形ABCD的对角线AC与BD相交于点O,E为AD的中点,连接OE,,,则( )
A.4 B. C.2 D.
3.(2023 乐山)如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连结OE.若AC=6,BD=8,则OE=( )
A.2 B. C.3 D.4
4.(2023 甘孜州)如图,在平面直角坐标系xOy中,菱形AOBC的顶点B在x轴的正半轴上,点A的坐标为,则点C的坐标为 .
5.(2022·四川自贡)如图,菱形对角线交点与坐标原点重合,点,则点的坐标为( )
A. B. C. D.
6.(2023 潍坊)如图,在直角坐标系中,菱形OABC的顶点A的坐标为(﹣2,0),∠AOC=60°.将菱形OABC沿x轴向右平移1个单位长度,再沿y轴向下平移1个单位长度,得到菱形O′A′B′C′,其中点B′的坐标为( )
A.(﹣2,﹣1) B.(﹣2,1) C.(﹣,1) D.(﹣,﹣1)
7.(2023 牡丹江)如图,在平面直角坐标系中,菱形ABCD的顶点A,B在x轴上,AB=2,A(1,0),∠DAB=60°,将菱形ABCD绕点A旋转90°后,得到菱形AB1C1D1,则点C1的坐标是 .
8.(2021 兰州)如图,菱形ABCD的对角线AC与BD相交于点O,点E在BD上,连接AE,CE,∠ABC=60°,∠BCE=15°,ED=4+4,则AD=( )
A.4 B. C.6 D.8
9.(2021 南充)如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,AE=BF=2,△DEF的周长为3,则AD的长为( )
A. B.2 C.+1 D.2﹣1
10.(2022·海南)如图,菱形中,点E是边的中点,垂直交的延长线于点F,若,则菱形的边长是( )
A.3 B.4 C.5 D.
11.(2022 呼和浩特)如图,四边形ABCD是菱形,∠DAB=60°,点E是DA中点,F是对角线AC上一点,且∠DEF=45°,则AF:FC的值是( )
A.3 B.+1 C.2+1 D.2+
12.(2023 十堰)如图,在菱形ABCD中,点E,F,G,H分别是AB,BC,CD,AD上的点,且BE=BF=CG=AH,若菱形的面积等于24,BD=8,则EF+GH= .
13.(2022 天津)如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE的中点,AF与DE相交于点G,则GF的长等于 .
14.(2022 贵港)如图,在边长为1的菱形ABCD中,∠ABC=60°,动点E在AB边上(与点A,B均不重合),点F在对角线AC上,CE与BF相交于点G,连接AG,DF,若AF=BE,则下列结论错误的是( )
A.DF=CE B.∠BGC=120°
C.AF2=EG EC D.AG的最小值为
15.(2021 包头)如图,在△ABC中,AB=AC,△DBC和△ABC关于直线BC对称,连接AD,与BC相交于点O,过点C作CE⊥CD,垂足为C,与AD相交于点E,若AD=8,BC=6,则的值为( )
A. B. C. D.
16.(2021·山东德州)下列选项中能使平行四边形ABCD成为菱形的是( )
A.AB=CD B.AB=BC C.∠BAD=90° D. AC=BD
17.(2022 襄阳)如图, ABCD的对角线AC和BD相交于点O,下列说法正确的是( )
A.若OB=OD,则 ABCD是菱形 B.若AC=BD,则 ABCD是菱形
C.若OA=OD,则 ABCD是菱形 D.若AC⊥BD,则 ABCD是菱形
18.(2023 齐齐哈尔)如图,在四边形ABCD中,AD=BC,AC⊥BD于点O.请添加一个条件: ,使四边形ABCD成为菱形.
19.(2020 广西)如图,将两条宽度均为2的纸条相交成30°角叠放,则重合部分构成的四边形ABCD的面积为 .
20.(2023 娄底模拟)如图,平行四边形ABCD中,对角线AC、BD相交于O,BD=2AD,E、F、G分别是OC、OD、AB的中点.下列结论:
①BE⊥AC;②BG=GF;
③△EFG≌△GBE;④EA平分∠GEF;
⑤四边形BEFG是菱形.其中正确的是 .(填写序号)
21.(2022 辽宁)如图,CD是△ABC的角平分线,过点D分别作AC,BC的平行线,交BC于点E,交AC于点F.若∠ACB=60°,CD=4,则四边形CEDF的周长是 .
22.(2022 北京)如图,在 ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.
(1)求证:四边形EBFD是平行四边形;
(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.
23.(2023 日照)如图,平行四边形ABCD中,点E是对角线AC上一点,连接BE,DE,且BE=DE.
(1)求证:四边形ABCD是菱形;
(2)若AB=10,tan∠BAC=2,求四边形ABCD的面积.
24.(2023 云南)如图,平行四边形ABCD中,AE、CF分别是∠BAD、∠BCD的平分线,且E、F分别在边BC、AD上,AE=AF.
(1)求证:四边形AECF是菱形;
(2)若∠ABC=60°,△ABE的面积等于,求平行线AB与DC间的距离.
四、正方形
笔记:
1. 定义:四条边都相等,四个角都是直角的四边形叫做正方形.
2.性质:(1)对边平行;
(2)四个角都是直角;
(3)四条边都相等;
(4)对角线互相垂直平分且相等,对角线平分对角;
(5) 两条对角线把正方形分成四个全等的等腰直角三角形;
(6)中心对称图形,轴对称图形.
3.面积:边长×边长=×对角线×对角线
4.判定:(1)有一个角是直角的菱形是正方形;(2)一组邻边相等的矩形是正方形;(3)对角线相等的菱形是正方形;(4)对角线互相垂直的矩形是正方形;(5)对角线互相垂直平分且相等的四边形是正方形;
(6)四条边都相等,四个角都是直角的四边形是正方形.
例题:
1.(2020 襄阳)已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形 D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
2.(2022·湖南衡阳)下列命题为假命题的是( )
A.对角线相等的平行四边形是矩形 B.对角线互相垂直的平行四边形是菱形
C.有一个内角是直角的平行四边形是正方形 D.有一组邻边相等的矩形是正方形
3.(2023 姜堰区一模)下列说法正确的是( )
A.菱形的对角线相等
B.矩形的对角线相等且互相平分
C.平行四边形是轴对称图形
D.对角线互相垂直且相等的四边形是正方形
4.(2023秋 越秀区校级月考)下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.菱形一条对角线平分一组对角
C.有两个角是直角,有一组对边平行的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
5.(2023 坪山区一模)如图,在菱形ABCD中,对角线AC,BD相交于点O,添加下列条件,能使菱形ABCD成为正方形的是( )
A.AC=BD B.AC⊥BD
C.AD=AB D.AC平分∠DAB
6.(2021·四川绵阳)如图,在边长为3的正方形中,,,则的长是( )
A.1 B. C. D.2
7.(2023 丹东)如图,在正方形ABCD中,AB=12,点E,F分别在边BC,CD上,AE与BF相交于点G,若BE=CF=5,则BG的长为 .
8.(2022 黄石)如图,正方形OABC的边长为,将正方形OABC绕原点O顺时针旋转45°,则点B的对应点B1的坐标为( )
A.(﹣,0) B.(,0) C.(0,) D.(0,2)
9.(2022 黄石)如图,正方形OABC的边长为,将正方形OABC绕原点O顺时针旋转45°,则点B的对应点B1的坐标为( )
A.(﹣,0) B.(,0) C.(0,) D.(0,2)
10.(2023 大连一模)如图,平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,则点B的纵坐标为( )
A.﹣2 B.﹣ C.﹣ D.﹣
11.(2022·重庆)如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
12.(2022 黔东南州)如图,折叠边长为4cm的正方形纸片ABCD,折痕是DM,点C落在点E处,分别延长ME、DE交AB于点F、G,若点M是BC边的中点,则FG= cm.
13.(2023 宜宾)如图,边长为6的正方形ABCD中,M为对角线BD上的一点,连接AM并延长交CD于点P,若PM=PC,则AM的长为( )
A.3(﹣1) B.3(3﹣2) C.6(﹣1) D.6(3﹣2)
14.(2023 台州)如图,⊙O的圆心O与正方形的中心重合,已知⊙O的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( )
A. B.2 C. D.
15.(2023 宁夏)如图,在边长为2的正方形ABCD中,点E在AD上,连接EB,EC.则图中阴影部分的面积是 .
16.(2023 安徽)如图,点E在正方形ABCD的对角线AC上,EF⊥AB于点F,连接DE并延长,交边BC于点M,交边AB的延长线于点G.若AF=2,FB=1,则MG=( )
A.2 B. C.+1 D.
17.(2023 攀枝花)如图,已知正方形ABCD的边长为3,点P是对角线BD上的一点,PF⊥AD于点F,PE⊥AB于点E,连接PC,当PE:PF=1:2时,则PC=( )
A. B.2 C. D.
18.(2023 河北)如图,在Rt△ABC中,AB=4,点M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC=( )
A.4 B.8 C.12 D.16
19.(2023 广西)如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
20.(2023 哈尔滨)如图,在正方形ABCD中,点E在CD上,连接AE,BE,F为BE的中点,连接CF,若 CF=,=,则AE的长为 .
21.(2023 大连)如图,正方形ABCD中,AB=3,点E在BC的延长线上,且CE=2.连接AE,∠DCE的平分线与AE相交于点F,连接DF,则DF的长为 .
22.(2023 怀化)如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3.则点P到直线AB的距离为 .
23.(2023 绵阳)如图,在边长为4的正方形ABCD中,点G是BC上的一点,且BG=3GC,DE⊥AG于点E,BF∥DE,且交AG于点F,则tan∠EDF的值为( )
A. B. C. D.
24.(2023 眉山)如图,在正方形ABCD中,点E是CD上一点,延长CB至点F,使BF=DE,连结AE,AF,EF,EF交AB于点K,过点A作AG⊥EF,垂足为点H,交CF于点G,连结HD,HC.
下列四个结论:
①AH=HC;
②HD=CD;
③∠FAB=∠DHE;
④AK HD=.
其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
25.(2023 青岛)如图,在正方形ABCD中,点E,F分别是AB,CD的中点,AF,DE相交于点M,G为BC上一点,N为EG的中点.若BG=3,CG=1,则线段MN的长度为( )
A. B. C.2 D.
五、中点四边形
1.(2020 菏泽)如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )
A.互相平分 B.相等
C.互相垂直 D.互相垂直平分
2.(2019 遵义)我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.已知四边形ABCD的中点四边形是正方形,对角线AC与BD的关系,下列说法正确的是( )
A.AC,BD相等且互相平分 B.AC,BD垂直且互相平分
C.AC,BD相等且互相垂直 D.AC,BD垂直且平分对角
3.(2022·广西玉林)若顺次连接四边形各边的中点所得的四边形是正方形,则四边形的两条对角线一定是( )
A.互相平分 B.互相垂直 C.互相平分且相等 D.互相垂直且相等
4.(2022·四川德阳)如图,在四边形中,点,,,分别是,,,边上的中点,则下列结论一定正确的是( )
A.四边形是矩形
B.四边形的内角和小于四边形的内角和
C.四边形的周长等于四边形的对角线长度之和
D.四边形的面积等于四边形面积的
5.(2023 滕州市校级开学)如图,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.要使四边形EFGH为矩形,可以添加的一个条件是( )
A.四边形ABCD是矩形 B.AC、BD互相平分
C.AC=BD D.AC⊥BD
6.(2023 越秀区校级开学)如图,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,E,F,G,H分别为边AB,BC,CD,DA的中点,则四边形EFGH的形状为 .
7.(2023秋 南山区校级月考)定义:对于一个四边形,我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点四边形”.如果原四边形的中点四边形是个正方形,我们把这个原四边形叫做“中方四边形”.
【概念理解】:
(1)下列四边形中一定是“中方四边形”的是 .
A.平行四边形;
B.矩形;
C.菱形;
D.正方形.
【性质探究】:
(2)如图1,四边形ABCD是“中方四边形”,观察图形,直接写出四边形ABCD的对角线AC,BD的关系.
【问题解决】:
(3)如图2.以锐角△ABC的两边AB,AC为边长,分别向外侧作正方形ABDE和正方形ACFG,连接BE,EG,GC.求证:四边形BCGE是“中方四边形”.
【拓展应用】:
如图3,已知四边形ABCD是“中方四边形”,M,N分别是AB,CD的中点.
(4)试探索AC与MN的数量关系,并说明理由.
(5)若AC=2,求AB+CD的最小值.
一、平行四边形
笔记:
1.定义:两组对边分别平行的四边形叫做平行四边形.
2.性质:(1)对边平行且相等;(2)对角相等;邻角互补;(3)对角线互相平分;(4)中心对称图形.
3.面积:
4.判定:(1)边:两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形.
(2)角:两组对角分别相等的四边形是平行四边形;任意两组邻角分别互补的四边形是平行四边形.
(3)边与角:一组对边平行,一组对角相等的四边形是平行四边形;
(4)对角线:对角线互相平分的四边形是平行四边形.
5.平行线的性质:(1)平行线间的距离都相等;(2)等底等高的平行四边形面积相等.
例题:
①平行四边形性质判定
1.(2023 益阳)如图, ABCD的对角线AC,BD交于点O,下列结论一定成立的是( )
A.OA=OB B.OA⊥OB C.OA=OC D.∠OBA=∠OBC
2.(2023 成都)如图,在 ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.AC=BD B.OA=OC C.AC⊥BD D.∠ADC=∠BCD
3.(2023 通辽)如图,用平移方法说明平行四边形的面积公式S=ah时,若△ABE平移到△DCF,a=4,h=3,则△ABE的平移距离为( )
A.3 B.4 C.5 D.12
4.(2022 益阳)如图,在 ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于点F,则BF的长为( )
A.5 B.4 C.3 D.2
5.(2020·湖南益阳)如图,的对角线,交于点,若,,则的长可能是( )
A. B. C. D.
6.(2022·广东广州)如图,在□ABCD中,AD=10,对角线AC 与BD相交于点O,AC+BD=22,则△BOC的周长为________
7.(2022·四川内江)如图,在 ABCD中,已知AB=12,AD=8,∠ABC的平分线BM交CD边于点M,则DM的长为( )
A.2 B.4 C.6 D.8
8.(2023 兰州)如图,在 ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE= °.
9.(2023 福建)如图,在 ABCD中,O为BD的中点,EF过点O且分别交AB,CD于点E,F.若AE=10,则CF的长为 .
10.(2023 凉山州)如图, ABCO的顶点O、A、C的坐标分别是(0,0)、(3,0)、(1,2).则顶点B的坐标是 .
11.(2023 丹阳市二模)平行四边形OABC在平面直角坐标系中的位置如图,∠AOC=45°,OA=1,OC=2,把平行四边形OABC绕点O逆时针旋转,使点A落在y轴正半轴上,则旋转后点B的对应点B′的坐标为( )
A.(,) B.(1,) C.(2,3) D.(,)
12.(2023 衡阳)如图,在四边形ABCD中,已知AD∥BC.添加下列条件不能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AB∥DC C.AB=DC D.∠A=∠C
13.(2022 达州)如图,在△ABC中,点D,E分别是AB,BC边的中点,点F在DE的延长线上.添加一个条件,使得四边形ADFC为平行四边形,则这个条件可以是( )
A.∠B=∠F B.DE=EF C.AC=CF D.AD=CF
14.(2020 衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
15.(2022 舟山)如图,在△ABC中,AB=AC=8.点E,F,G分别在边AB,BC,AC上,EF∥AC,GF∥AB,则四边形AEFG的周长是( )
A.32 B.24 C.16 D.8
16.(2023 聊城)如图,在 ABCD中,BC的垂直平分线EO交AD于点E,交BC于点O,连接BE,CE,过点C作CF∥BE,交EO的延长线于点F,连接BF.若AD=8,CE=5,则四边形BFCE的面积为 .
17.(2022 临沂)如图,在正六边形ABCDEF中,M,N是对角线BE上的两点.添加下列条件中的一个:①BM=EN;②∠FAN=∠CDM;③AM=DN;④∠AMB=∠DNE.能使四边形AMDN是平行四边形的是 (填上所有符合要求的条件的序号).
18.(2023 广安)如图,在四边形ABCD中,AC与BD交于点O,BE⊥AC,DF⊥AC,垂足分别为点E、F,且AF=CE,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.
19.(2023 杭州)如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形.
(2)若△ABE的面积等于2,求△CFO的面积.
20.(2023 扬州)如图,点E、F、G、H分别是平行四边形ABCD各边的中点,连接AF、CE相交于点M,连接AG、CH相交于点N.
(1)求证:四边形AMCN是平行四边形;
(2)若 AMCN的面积为4,求 ABCD的面积.
21.(2022 温州)如图,在△ABC中,AD⊥BC于点D,E,F分别是AC,AB的中点,O是DF的中点,EO的延长线交线段BD于点G,连结DE,EF,FG.
(1)求证:四边形DEFG是平行四边形.
(2)当AD=5,tan∠EDC=时,求FG的长.
22.(2021 北京)如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE∥DC,EF⊥AB,垂足为F.
(1)求证:四边形AECD是平行四边形;
(2)若AE平分∠BAC,BE=5,cosB=,求BF和AD的长.
②中位线
1.(2023 云南)如图,A、B两点被池塘隔开,A、B、C三点不共线.设AC、BC的中点分别为M、N.若MN=3米,则AB=( )
A.4米 B.6米 C.8米 D.10米
2.(2022 眉山)在△ABC中,AB=4,BC=6,AC=8,点D,E,F分别为边AB,AC,BC的中点,则△DEF的周长为( )
A.9 B.12 C.14 D.16
3.(2022·浙江丽水)如图,在中,D,E,F分别是,,的中点.若,,则四边形的周长是( )
A.28 B.14 C.10 D.7
4.(2022·江苏扬州)“做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片,第1次折叠使点落在边上的点处,折痕交于点;第2次折叠使点落在点处,折痕交于点.若,则_____________.
5.(2022 镇江)如图,在△ABC和△ABD中,∠ACB=∠ADB=90°,E、F、G分别为AB、AC、BC的中点,若DE=1,则FG= .
6.(2023 武功县模拟)如图,在Rt△ABC中,∠BAC=90°,AD是△ABC的中线,点E,F分别是AD,AC的中点,连接EF,若EF=3,则AD的长为 .
7.(2020·贵州毕节)如图,在矩形中,对角线,相交于点,点,分别是,的中点,连接,若,,则的长是( )
A. B. C. D.
8.(2022·黑龙江哈尔滨)如图,菱形的对角线相交于点O,点E在上,连接,点F为的中点,连接,若,,,则线段的长为___________.
9.(2022·广东广州)如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A. B.C. D.
10.(2022·浙江宁波)如图,在中,D为斜边的中点,E为上一点,F为中点.若,,则的长为( )
A. B.3 C. D.4
11.(2022 安顺)如图,在△ABC中,AC=2,∠ACB=120°,D是边AB的中点,E是边BC上一点,若DE平分△ABC的周长,则DE的长为( )
A. B. C. D.
12.(2023 铜仁市模拟)已知,Rt△ABC中,∠ABC=90°,AB=3,AD平分∠BAC,AD⊥BD,垂足为D,E为BC中点,连结DE,DE=1,则AD的值为( )
A. B. C. D.
13.(2023 广州)如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点M是边AC上一动点,点D,E分别是AB,MB的中点,当AM=2.4时,DE的长是 .若点N在边BC上,且CN=AM,点F,G分别是MN,AN的中点,当AM>2.4时,四边形DEFG面积S的取值范围是 .
二、矩形
笔记:
1.定义:有一个角是直角的平行四边形叫做矩形.
2.性质:(1)具有平行四边形的所有性质;(2)四个角都是直角;
(3)对角线互相平分且相等;(4)中心对称图形,轴对称图形.
3.面积:
4.判定:(1) 有一个角是直角的平行四边形是矩形.
(2)对角线相等的平行四边形是矩形.
(3)有三个角是直角的四边形是矩形.
5.由矩形得直角三角形的性质:
(1)直角三角形斜边上的中线等于斜边的一半;
(2)直角三角形中,30度角所对应的直角边等于斜边的一半.
例题:
①矩形判定、性质
1.(2023 襄阳)如图,矩形ABCD的对角线相交于点O,下列结论一定正确的是( )
A.AC平分∠BAD B.AB=BC
C.AC=BD D.AC⊥BD
2.(2023 呼和浩特)如图,矩形ABCD中,对角线BD的垂直平分线MN分别交AD,BC于点M,N.若AM=1,BN=2,则BD的长为( )
A. B.3 C. D.
3.(2022·青海)如图矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=3,BC=4,则图中阴影部分的面积为_____.
4.(2020·青海)如图,在矩形中,对角线,相交于点,已知,,则的长为________cm.
5.(2023 杭州)如图,矩形ABCD的对角线AC,BD相交于点O.若∠AOB=60°,则=( )
A. B. C. D.
6.(2021·辽宁鞍山)如图,矩形ABCD中,,对角线AC,BD交于点O,,垂足为点H,若,则AD的长为_______________.
7.(2022·四川达州)如图,点E在矩形的边上,将沿翻折,点A恰好落在边上的点F处,若,,则的长为( )
A.9 B.12 C.15 D.18
8.(2023 南通)如图,四边形ABCD是矩形,分别以点B,D为圆心,线段BC,DC长为半径画弧,两弧相交于点E,连接BE,DE,BD.若AB=4,BC=8,则∠ABE的正切值为( )
A. B. C. D.
9.(2023 台州)如图,矩形ABCD中,AB=4,AD=6.在边AD上取一点E,使BE=BC,过点C作CF⊥BE,垂足为点F,则BF的长为 .
10.(2023 苏州)如图,在平面直角坐标系中,点A的坐标为(9,0),点C的坐标为(0,3),以OA,OC为边作矩形OABC.动点E,F分别从点O,B同时出发,以每秒1个单位长度的速度沿OA,BC向终点A,C移动.当移动时间为4秒时,AC EF的值为( )
A. B.9 C.15 D.30
11.(2023 贵州)如图,在矩形ABCD中,点E为矩形内一点,且AB=1,AD=,∠BAE=75°,∠BCE=60°,则四边形ABCE的面积是 .
12.(2023 河南)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为 .
13.(2023 哈尔滨)矩形ABCD的对角线AC,BD相交于点O,点F在矩形ABCD边上,连接OF.若∠ADB=38°,∠BOF=30°,则∠AOF= .
14.(2022 陕西)在下列条件中,能够判定 ABCD为矩形的是( )
A.AB=AD B.AC⊥BD C.AB=AC D.AC=BD
15.(2020·湖北)已知中,下列条件:①;②;③;④平分,其中能说明是矩形的是( )
A.① B.② C.③ D.④
16.(2023 上海)在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD为矩形的是( )
A.AB∥CD B.AD=BC C.∠A=∠B D.∠A=∠D
17.(2023 大庆)如图,在平行四边形ABCD中,E为线段CD的中点,连接AC,AE,延长AE,BC交于点F,连接DF,∠ACF=90°.
(1)求证:四边形ACFD是矩形;
(2)若CD=13,CF=5,求四边形ABCE的面积.
18.(2023 北京)如图,在 ABCD中,点E,F分别在BC,AD上,BE=DF,AC=EF.
(1)求证:四边形AECF是矩形;
(2)若AE=BE,AB=2,tan∠ACB=,求BC的长.
19.(2023 温州)如图,已知矩形ABCD,点E在CB延长线上,点F在BC延长线上,过点F作FH⊥EF交ED的延长线于点H,连结AF交EH于点G,GE=GH.
(1)求证:BE=CF;
(2)当=,AD=4时,求EF的长.
20.(2022 十堰)如图, ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
(1)求证:BE=DF;
(2)设=k,当k为何值时,四边形DEBF是矩形?请说明理由.
②斜边中线
1.(2023 株洲)一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,点D为边AB的中点,点A、B对应的刻度为1、7,则CD=( )
A.3.5cm B.3cm C.4.5cm D.6cm
2.(2022 永州)如图,在Rt△ABC中,∠ABC=90°,∠C=60°,点D为边AC的中点,BD=2,则BC的长为( )
A. B.2 C.2 D.4
3.(2018 贺州)如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,AD=ED=3,则BC的长为( )
A.3 B.3 C.6 D.6
4.(2023 荆州)如图,CD为Rt△ABC斜边AB上的中线,E为AC的中点.若AC=8,CD=5,则DE= .
5.(2019 陕西)如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为( )
A.19° B.33° C.34° D.43°
6.(2022 雁塔区校级模拟)如图,在△ABC中,∠ACB=90°,∠A=22.5°,CD⊥AB于点D,点E为AB的中点,连接CE,若CD=2,则AB的长为( )
A.4 B.2 C.4 D.6
7.(2022 荆州)如图,在Rt△ABC中,∠ACB=90°,通过尺规作图得到的直线MN分别交AB,AC于D,E,连接CD.若CE=AE=1,则CD= .
8.(2023 雁塔区校级模拟)如图,△ABC中,∠ACB=90°,点E为AB的中点,点D在BC上,且AD=BD,AD、CE相交于点F,若∠B=20°,则∠DFE等于( )
A.70° B.60° C.50° D.40°
9.(2023 长安区校级二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,CD是△ABC的中线,E是CD的中点,连接AE,BE,若AE⊥BE,垂足为E,则AC的长为 .
10.(2021 蜀山区模拟)如图,△ABC中,∠C=90°,AC=10,BC=8,线段DE的两个端点D、E分别在边AC,BC上滑动,且DE=6,若点M、N分别是DE、AB的中点,则MN的最小值为( )
A.10﹣ B.﹣3 C.2﹣6 D.3
11.(2022 杭州)如图,在Rt△ACB中,∠ACB=90°,点M为边AB的中点,点E在线段AM上,EF⊥AC于点F,连接CM,CE.已知∠A=50°,∠ACE=30°.
(1)求证:CE=CM.
(2)若AB=4,求线段FC的长.
三、菱形
笔记:
1. 定义:有一组邻边相等的平行四边形叫做菱形.
2.性质:(1)具有平行四边形的一切性质;
(2)四条边相等;
(3)两条对角线互相平分且垂直,并且每一条对角线平分一组对角;
(4)中心对称图形,轴对称图形.
3.面积:
4.判定:(1)一组邻边相等的平行四边形是菱形;
(2)对角线互相垂直的平行四边形是菱形;
(3)四边相等的四边形是菱形.
例题:
1.(2021·广西柳州)如图,在菱形中,对角线,则的面积为( )
A.9 B.10 C.11 D.12
2.(2022·甘肃兰州)如图,菱形ABCD的对角线AC与BD相交于点O,E为AD的中点,连接OE,,,则( )
A.4 B. C.2 D.
3.(2023 乐山)如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连结OE.若AC=6,BD=8,则OE=( )
A.2 B. C.3 D.4
4.(2023 甘孜州)如图,在平面直角坐标系xOy中,菱形AOBC的顶点B在x轴的正半轴上,点A的坐标为,则点C的坐标为 .
5.(2022·四川自贡)如图,菱形对角线交点与坐标原点重合,点,则点的坐标为( )
A. B. C. D.
6.(2023 潍坊)如图,在直角坐标系中,菱形OABC的顶点A的坐标为(﹣2,0),∠AOC=60°.将菱形OABC沿x轴向右平移1个单位长度,再沿y轴向下平移1个单位长度,得到菱形O′A′B′C′,其中点B′的坐标为( )
A.(﹣2,﹣1) B.(﹣2,1) C.(﹣,1) D.(﹣,﹣1)
7.(2023 牡丹江)如图,在平面直角坐标系中,菱形ABCD的顶点A,B在x轴上,AB=2,A(1,0),∠DAB=60°,将菱形ABCD绕点A旋转90°后,得到菱形AB1C1D1,则点C1的坐标是 .
8.(2021 兰州)如图,菱形ABCD的对角线AC与BD相交于点O,点E在BD上,连接AE,CE,∠ABC=60°,∠BCE=15°,ED=4+4,则AD=( )
A.4 B. C.6 D.8
9.(2021 南充)如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,AE=BF=2,△DEF的周长为3,则AD的长为( )
A. B.2 C.+1 D.2﹣1
10.(2022·海南)如图,菱形中,点E是边的中点,垂直交的延长线于点F,若,则菱形的边长是( )
A.3 B.4 C.5 D.
11.(2022 呼和浩特)如图,四边形ABCD是菱形,∠DAB=60°,点E是DA中点,F是对角线AC上一点,且∠DEF=45°,则AF:FC的值是( )
A.3 B.+1 C.2+1 D.2+
12.(2023 十堰)如图,在菱形ABCD中,点E,F,G,H分别是AB,BC,CD,AD上的点,且BE=BF=CG=AH,若菱形的面积等于24,BD=8,则EF+GH= .
13.(2022 天津)如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE的中点,AF与DE相交于点G,则GF的长等于 .
14.(2022 贵港)如图,在边长为1的菱形ABCD中,∠ABC=60°,动点E在AB边上(与点A,B均不重合),点F在对角线AC上,CE与BF相交于点G,连接AG,DF,若AF=BE,则下列结论错误的是( )
A.DF=CE B.∠BGC=120°
C.AF2=EG EC D.AG的最小值为
15.(2021 包头)如图,在△ABC中,AB=AC,△DBC和△ABC关于直线BC对称,连接AD,与BC相交于点O,过点C作CE⊥CD,垂足为C,与AD相交于点E,若AD=8,BC=6,则的值为( )
A. B. C. D.
16.(2021·山东德州)下列选项中能使平行四边形ABCD成为菱形的是( )
A.AB=CD B.AB=BC C.∠BAD=90° D. AC=BD
17.(2022 襄阳)如图, ABCD的对角线AC和BD相交于点O,下列说法正确的是( )
A.若OB=OD,则 ABCD是菱形 B.若AC=BD,则 ABCD是菱形
C.若OA=OD,则 ABCD是菱形 D.若AC⊥BD,则 ABCD是菱形
18.(2023 齐齐哈尔)如图,在四边形ABCD中,AD=BC,AC⊥BD于点O.请添加一个条件: ,使四边形ABCD成为菱形.
19.(2020 广西)如图,将两条宽度均为2的纸条相交成30°角叠放,则重合部分构成的四边形ABCD的面积为 .
20.(2023 娄底模拟)如图,平行四边形ABCD中,对角线AC、BD相交于O,BD=2AD,E、F、G分别是OC、OD、AB的中点.下列结论:
①BE⊥AC;②BG=GF;
③△EFG≌△GBE;④EA平分∠GEF;
⑤四边形BEFG是菱形.其中正确的是 .(填写序号)
21.(2022 辽宁)如图,CD是△ABC的角平分线,过点D分别作AC,BC的平行线,交BC于点E,交AC于点F.若∠ACB=60°,CD=4,则四边形CEDF的周长是 .
22.(2022 北京)如图,在 ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.
(1)求证:四边形EBFD是平行四边形;
(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.
23.(2023 日照)如图,平行四边形ABCD中,点E是对角线AC上一点,连接BE,DE,且BE=DE.
(1)求证:四边形ABCD是菱形;
(2)若AB=10,tan∠BAC=2,求四边形ABCD的面积.
24.(2023 云南)如图,平行四边形ABCD中,AE、CF分别是∠BAD、∠BCD的平分线,且E、F分别在边BC、AD上,AE=AF.
(1)求证:四边形AECF是菱形;
(2)若∠ABC=60°,△ABE的面积等于,求平行线AB与DC间的距离.
四、正方形
笔记:
1. 定义:四条边都相等,四个角都是直角的四边形叫做正方形.
2.性质:(1)对边平行;
(2)四个角都是直角;
(3)四条边都相等;
(4)对角线互相垂直平分且相等,对角线平分对角;
(5) 两条对角线把正方形分成四个全等的等腰直角三角形;
(6)中心对称图形,轴对称图形.
3.面积:边长×边长=×对角线×对角线
4.判定:(1)有一个角是直角的菱形是正方形;(2)一组邻边相等的矩形是正方形;(3)对角线相等的菱形是正方形;(4)对角线互相垂直的矩形是正方形;(5)对角线互相垂直平分且相等的四边形是正方形;
(6)四条边都相等,四个角都是直角的四边形是正方形.
例题:
1.(2020 襄阳)已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形 D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
2.(2022·湖南衡阳)下列命题为假命题的是( )
A.对角线相等的平行四边形是矩形 B.对角线互相垂直的平行四边形是菱形
C.有一个内角是直角的平行四边形是正方形 D.有一组邻边相等的矩形是正方形
3.(2023 姜堰区一模)下列说法正确的是( )
A.菱形的对角线相等
B.矩形的对角线相等且互相平分
C.平行四边形是轴对称图形
D.对角线互相垂直且相等的四边形是正方形
4.(2023秋 越秀区校级月考)下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.菱形一条对角线平分一组对角
C.有两个角是直角,有一组对边平行的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
5.(2023 坪山区一模)如图,在菱形ABCD中,对角线AC,BD相交于点O,添加下列条件,能使菱形ABCD成为正方形的是( )
A.AC=BD B.AC⊥BD
C.AD=AB D.AC平分∠DAB
6.(2021·四川绵阳)如图,在边长为3的正方形中,,,则的长是( )
A.1 B. C. D.2
7.(2023 丹东)如图,在正方形ABCD中,AB=12,点E,F分别在边BC,CD上,AE与BF相交于点G,若BE=CF=5,则BG的长为 .
8.(2022 黄石)如图,正方形OABC的边长为,将正方形OABC绕原点O顺时针旋转45°,则点B的对应点B1的坐标为( )
A.(﹣,0) B.(,0) C.(0,) D.(0,2)
9.(2022 黄石)如图,正方形OABC的边长为,将正方形OABC绕原点O顺时针旋转45°,则点B的对应点B1的坐标为( )
A.(﹣,0) B.(,0) C.(0,) D.(0,2)
10.(2023 大连一模)如图,平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,则点B的纵坐标为( )
A.﹣2 B.﹣ C.﹣ D.﹣
11.(2022·重庆)如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
12.(2022 黔东南州)如图,折叠边长为4cm的正方形纸片ABCD,折痕是DM,点C落在点E处,分别延长ME、DE交AB于点F、G,若点M是BC边的中点,则FG= cm.
13.(2023 宜宾)如图,边长为6的正方形ABCD中,M为对角线BD上的一点,连接AM并延长交CD于点P,若PM=PC,则AM的长为( )
A.3(﹣1) B.3(3﹣2) C.6(﹣1) D.6(3﹣2)
14.(2023 台州)如图,⊙O的圆心O与正方形的中心重合,已知⊙O的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( )
A. B.2 C. D.
15.(2023 宁夏)如图,在边长为2的正方形ABCD中,点E在AD上,连接EB,EC.则图中阴影部分的面积是 .
16.(2023 安徽)如图,点E在正方形ABCD的对角线AC上,EF⊥AB于点F,连接DE并延长,交边BC于点M,交边AB的延长线于点G.若AF=2,FB=1,则MG=( )
A.2 B. C.+1 D.
17.(2023 攀枝花)如图,已知正方形ABCD的边长为3,点P是对角线BD上的一点,PF⊥AD于点F,PE⊥AB于点E,连接PC,当PE:PF=1:2时,则PC=( )
A. B.2 C. D.
18.(2023 河北)如图,在Rt△ABC中,AB=4,点M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC=( )
A.4 B.8 C.12 D.16
19.(2023 广西)如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
20.(2023 哈尔滨)如图,在正方形ABCD中,点E在CD上,连接AE,BE,F为BE的中点,连接CF,若 CF=,=,则AE的长为 .
21.(2023 大连)如图,正方形ABCD中,AB=3,点E在BC的延长线上,且CE=2.连接AE,∠DCE的平分线与AE相交于点F,连接DF,则DF的长为 .
22.(2023 怀化)如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3.则点P到直线AB的距离为 .
23.(2023 绵阳)如图,在边长为4的正方形ABCD中,点G是BC上的一点,且BG=3GC,DE⊥AG于点E,BF∥DE,且交AG于点F,则tan∠EDF的值为( )
A. B. C. D.
24.(2023 眉山)如图,在正方形ABCD中,点E是CD上一点,延长CB至点F,使BF=DE,连结AE,AF,EF,EF交AB于点K,过点A作AG⊥EF,垂足为点H,交CF于点G,连结HD,HC.
下列四个结论:
①AH=HC;
②HD=CD;
③∠FAB=∠DHE;
④AK HD=.
其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
25.(2023 青岛)如图,在正方形ABCD中,点E,F分别是AB,CD的中点,AF,DE相交于点M,G为BC上一点,N为EG的中点.若BG=3,CG=1,则线段MN的长度为( )
A. B. C.2 D.
五、中点四边形
1.(2020 菏泽)如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )
A.互相平分 B.相等
C.互相垂直 D.互相垂直平分
2.(2019 遵义)我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.已知四边形ABCD的中点四边形是正方形,对角线AC与BD的关系,下列说法正确的是( )
A.AC,BD相等且互相平分 B.AC,BD垂直且互相平分
C.AC,BD相等且互相垂直 D.AC,BD垂直且平分对角
3.(2022·广西玉林)若顺次连接四边形各边的中点所得的四边形是正方形,则四边形的两条对角线一定是( )
A.互相平分 B.互相垂直 C.互相平分且相等 D.互相垂直且相等
4.(2022·四川德阳)如图,在四边形中,点,,,分别是,,,边上的中点,则下列结论一定正确的是( )
A.四边形是矩形
B.四边形的内角和小于四边形的内角和
C.四边形的周长等于四边形的对角线长度之和
D.四边形的面积等于四边形面积的
5.(2023 滕州市校级开学)如图,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.要使四边形EFGH为矩形,可以添加的一个条件是( )
A.四边形ABCD是矩形 B.AC、BD互相平分
C.AC=BD D.AC⊥BD
6.(2023 越秀区校级开学)如图,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,E,F,G,H分别为边AB,BC,CD,DA的中点,则四边形EFGH的形状为 .
7.(2023秋 南山区校级月考)定义:对于一个四边形,我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点四边形”.如果原四边形的中点四边形是个正方形,我们把这个原四边形叫做“中方四边形”.
【概念理解】:
(1)下列四边形中一定是“中方四边形”的是 .
A.平行四边形;
B.矩形;
C.菱形;
D.正方形.
【性质探究】:
(2)如图1,四边形ABCD是“中方四边形”,观察图形,直接写出四边形ABCD的对角线AC,BD的关系.
【问题解决】:
(3)如图2.以锐角△ABC的两边AB,AC为边长,分别向外侧作正方形ABDE和正方形ACFG,连接BE,EG,GC.求证:四边形BCGE是“中方四边形”.
【拓展应用】:
如图3,已知四边形ABCD是“中方四边形”,M,N分别是AB,CD的中点.
(4)试探索AC与MN的数量关系,并说明理由.
(5)若AC=2,求AB+CD的最小值.
同课章节目录
