2024 年 数学中考知识点专项练习:一次函数中存在性问题 (无答案)
文档属性
| 名称 | 2024 年 数学中考知识点专项练习:一次函数中存在性问题 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 401.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 20:31:08 | ||
图片预览


文档简介
2023-2024学年初中数学中考知识点专项练习:一次函数中存在性问题
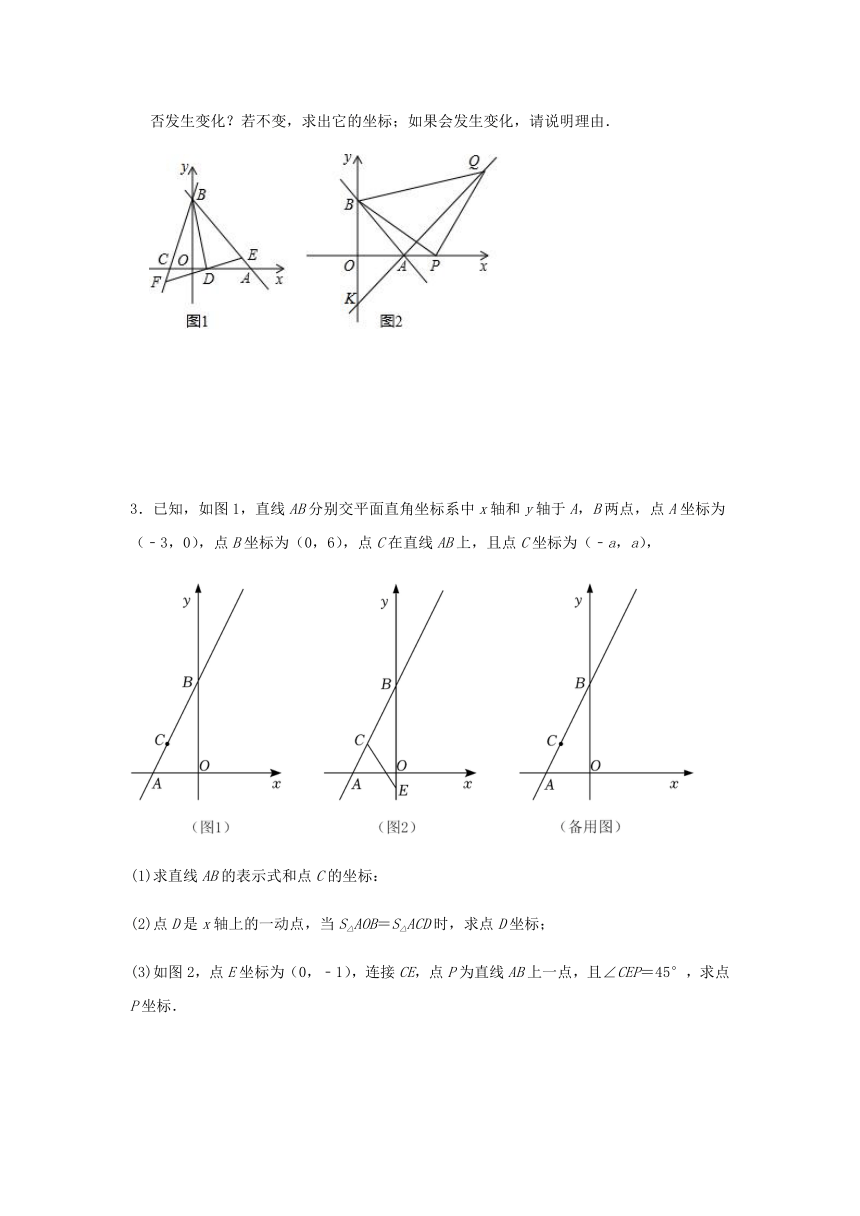
1.如图,已知一次函数y=﹣x+6的图象与坐标轴交于A、B两点,AE平分∠BAO,交x轴于点E.
(1)求点B的坐标及直线AE的表达式;
(2)过点B作BF⊥AE,垂足为F,在y轴上有一点P,使线段PE+PF的值最小,求点P的坐标;
(3)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F,以EF为边作正方形EFMN,当点M落在坐标轴上时,求E点坐标.
2、如图1,直线y=﹣x+b分别与x轴,y轴交于A(6,0),B两点,过点B的另一直线交x轴的负半轴于点C,且OB:OC=3:1
(1)求直线BC的解析式;
(2)直线y=ax﹣a(a≠0)交AB于点E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使S△BDE=S△BDF?若存在,求出a的值;若不存在,请说明理由;
(3)如图2,点P为A点右侧x轴上一动点,以P为直角顶点,BP为腰在第一象限内作等腰直角三角形△BPQ,连接QA并延长交y轴于点K.当P点运动时,K点的位置是否发生变化?若不变,求出它的坐标;如果会发生变化,请说明理由.
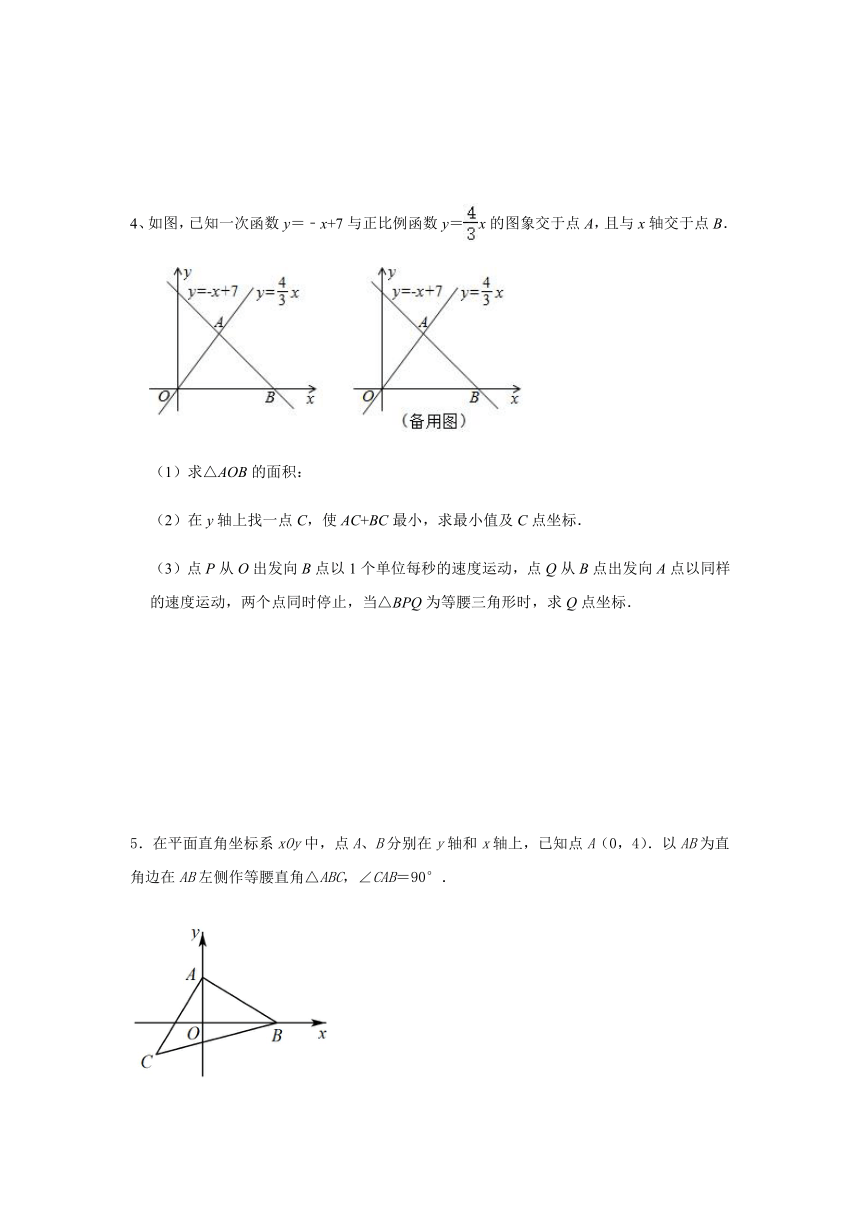
3.已知,如图1,直线AB分别交平面直角坐标系中x轴和y轴于A,B两点,点A坐标为(﹣3,0),点B坐标为(0,6),点C在直线AB上,且点C坐标为(﹣a,a),
(1)求直线AB的表示式和点C的坐标:
(2)点D是x轴上的一动点,当S△AOB=S△ACD时,求点D坐标;
(3)如图2,点E坐标为(0,﹣1),连接CE,点P为直线AB上一点,且∠CEP=45°,求点P坐标.
4、如图,已知一次函数y=﹣x+7与正比例函数y=x的图象交于点A,且与x轴交于点B.
(1)求△AOB的面积:
(2)在y轴上找一点C,使AC+BC最小,求最小值及C点坐标.
(3)点P从O出发向B点以1个单位每秒的速度运动,点Q从B点出发向A点以同样的速度运动,两个点同时停止,当△BPQ为等腰三角形时,求Q点坐标.
5.在平面直角坐标系xOy中,点A、B分别在y轴和x轴上,已知点A(0,4).以AB为直角边在AB左侧作等腰直角△ABC,∠CAB=90°.
(1)当点B在x轴正半轴上,且AB=8时
①求AB解析式;
②求C点坐标;
(2)当点B在x轴上运动时,连接OC,求AC+OC的最小值及此时B点坐标.
6.如图,直线与过点的直线交于点,与x轴交于点B,轴于点D.
(1)求直线的函数表达式;
(2)点P是线段上一动点,若,求点P的坐标;
(3)在x轴上是否存在点P,使得以B、C、P为顶点的三角形是等腰三角形 若存在,请直接写出点P的坐标;若不存在,请说明理由.
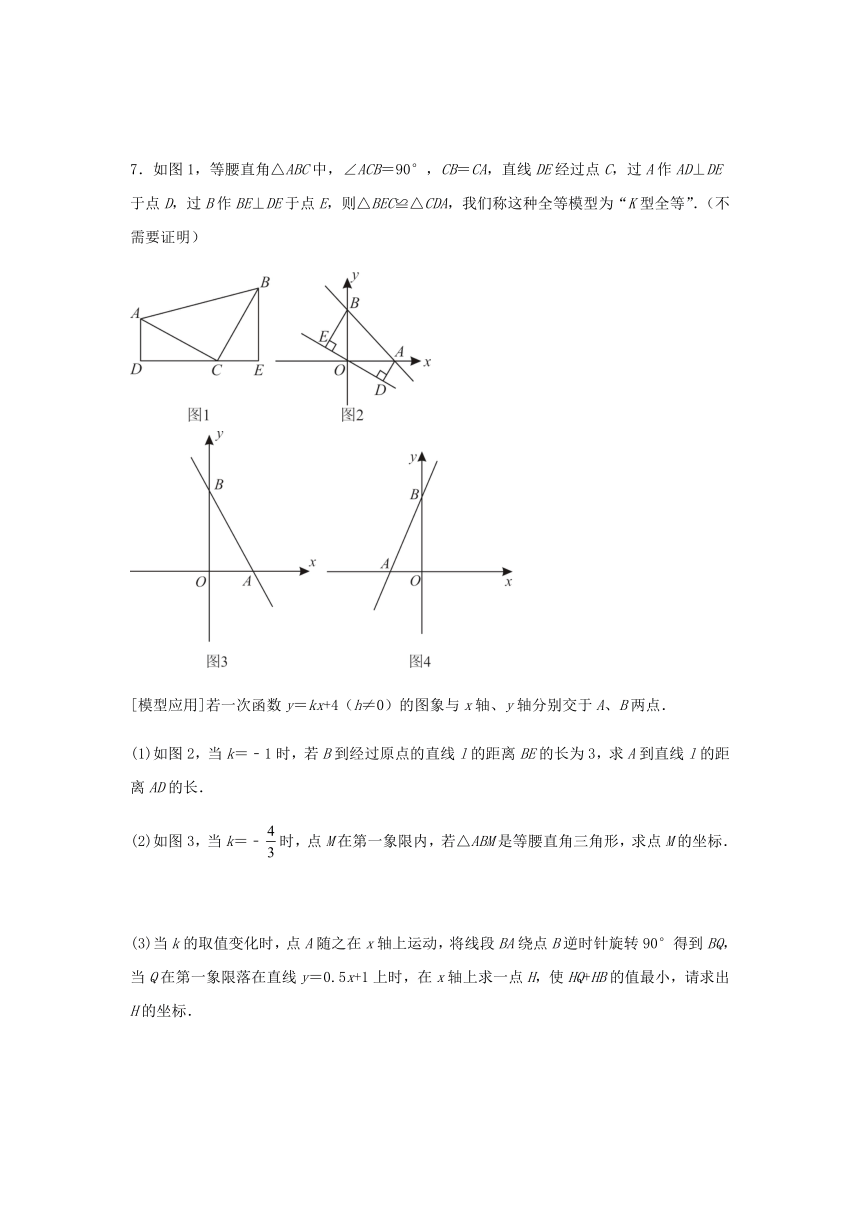
7.如图1,等腰直角△ABC中,∠ACB=90°,CB=CA,直线DE经过点C,过A作AD⊥DE于点D,过B作BE⊥DE于点E,则△BEC≌△CDA,我们称这种全等模型为“K型全等”.(不需要证明)
[模型应用]若一次函数y=kx+4(h≠0)的图象与x轴、y轴分别交于A、B两点.
(1)如图2,当k=﹣1时,若B到经过原点的直线l的距离BE的长为3,求A到直线l的距离AD的长.
(2)如图3,当k=﹣时,点M在第一象限内,若△ABM是等腰直角三角形,求点M的坐标.
(3)当k的取值变化时,点A随之在x轴上运动,将线段BA绕点B逆时针旋转90°得到BQ,当Q在第一象限落在直线y=0.5x+1上时,在x轴上求一点H,使HQ+HB的值最小,请求出H的坐标.
8.如图1,在平面直角坐标系xOy中,直线AB交y轴于点A(0,3),交x轴于点B(﹣4,0).
(1)求直线AB的函数表达式;
(2)如图2,在线段OB上有一点C(点C不与点O、点B重合),将AOC沿AC折叠,使点O落在AB上,记作点D,在BD上方,以BD为斜边作等腰直角三角形BDF,求点F的坐标;
(3)在(2)的条件下,如图3,在平面内是否存在一点E,使得以点A,B,E为顶点的三角形与ABC全等(点E不与点C重合),若存在,请直接写出满足条件的所有点E的坐标,若不存在,请说明理由.
9.如图,四边形是矩形,点A、C分别在x轴、y轴上,是绕点O顺时针旋转得到的,点D在x轴上,直线交y轴于点F,交于点H,点B的坐标为.
(1)求直线的表达式;
(2)求的面积;
(3)点M在x轴上,平面内处否存在点N,使以点D、F、M、N为顶点的四边形是矩形 若存在,请直接写出点N的坐标;若不存在,请说明理由.
10.在平面直角坐标系中,直线y=﹣3x﹣交x轴于点A,交y轴于点B,直线y=﹣x+3交x轴于点C,交y轴于点D.
(1)如图1,连接BC,求BCD的面积;
(2)如图2,在直线y=﹣x+3上存在点E,使得∠ABE=45°,求点E的坐标;
(3)如图3,在(2)的条件下,连接OE,过点E作CD的垂线交y轴于点F,点P在直线EF上,在平面中存在一点Q,使得以OE为一边,O,E,P,Q为顶点的四边形为菱形,请直接写出点Q的坐标.
11.如图,在平面直角坐标系中,一次函数的图像与x轴交于点A,一次函数的图像与x轴交于点B,与交于点C.点P是y轴上一点,点Q是直线上一点.
(1)求的面积;
(2)若点P在y轴的负半轴上,且是轴对称图形,求点P的坐标;
(3)若以P、Q、B、C为顶点的四边形是平行四边形,直接写出点Q的坐标.
12.如图,在平面直角坐标系中,正方形的边,分别在轴,轴的正半轴上,直线经过线段的中点,与轴交于点,是线段上一点,作点关于直线的对称点,连接,,.设点的坐标为.
(1)写出点B的坐标是______;
(2)当时,求点E的坐标;
(3)在点E的整个运动过程中,
①当四边形为菱形时,求点E的坐标;
②若N为平面内一点,当以B,E,F,N为顶点的四边形为矩形时,m的值为______.(请直接写出答案)
13.已知直线与x轴交于点A,直线与x轴交于点B,直线交于点C,且C点的横坐标为1.
(1)求直线的解析式.
(2)如图1,过点A作x轴的垂线,若点P为垂线上的一个动点,点,若,求此时点P的坐标.
(3)如图2,点E的坐标为,将直线绕点C逆时针旋转,使旋转后的直线刚好过点E,过点C作平行于x轴的直线,点分别为直线上的两个动点,是否存在点,使得是以M点为直角顶点的等腰直角三角形,若存在,直接写出N点的坐标;若不存在,请说明理由.
1.如图,已知一次函数y=﹣x+6的图象与坐标轴交于A、B两点,AE平分∠BAO,交x轴于点E.
(1)求点B的坐标及直线AE的表达式;
(2)过点B作BF⊥AE,垂足为F,在y轴上有一点P,使线段PE+PF的值最小,求点P的坐标;
(3)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F,以EF为边作正方形EFMN,当点M落在坐标轴上时,求E点坐标.
2、如图1,直线y=﹣x+b分别与x轴,y轴交于A(6,0),B两点,过点B的另一直线交x轴的负半轴于点C,且OB:OC=3:1
(1)求直线BC的解析式;
(2)直线y=ax﹣a(a≠0)交AB于点E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使S△BDE=S△BDF?若存在,求出a的值;若不存在,请说明理由;
(3)如图2,点P为A点右侧x轴上一动点,以P为直角顶点,BP为腰在第一象限内作等腰直角三角形△BPQ,连接QA并延长交y轴于点K.当P点运动时,K点的位置是否发生变化?若不变,求出它的坐标;如果会发生变化,请说明理由.
3.已知,如图1,直线AB分别交平面直角坐标系中x轴和y轴于A,B两点,点A坐标为(﹣3,0),点B坐标为(0,6),点C在直线AB上,且点C坐标为(﹣a,a),
(1)求直线AB的表示式和点C的坐标:
(2)点D是x轴上的一动点,当S△AOB=S△ACD时,求点D坐标;
(3)如图2,点E坐标为(0,﹣1),连接CE,点P为直线AB上一点,且∠CEP=45°,求点P坐标.
4、如图,已知一次函数y=﹣x+7与正比例函数y=x的图象交于点A,且与x轴交于点B.
(1)求△AOB的面积:
(2)在y轴上找一点C,使AC+BC最小,求最小值及C点坐标.
(3)点P从O出发向B点以1个单位每秒的速度运动,点Q从B点出发向A点以同样的速度运动,两个点同时停止,当△BPQ为等腰三角形时,求Q点坐标.
5.在平面直角坐标系xOy中,点A、B分别在y轴和x轴上,已知点A(0,4).以AB为直角边在AB左侧作等腰直角△ABC,∠CAB=90°.
(1)当点B在x轴正半轴上,且AB=8时
①求AB解析式;
②求C点坐标;
(2)当点B在x轴上运动时,连接OC,求AC+OC的最小值及此时B点坐标.
6.如图,直线与过点的直线交于点,与x轴交于点B,轴于点D.
(1)求直线的函数表达式;
(2)点P是线段上一动点,若,求点P的坐标;
(3)在x轴上是否存在点P,使得以B、C、P为顶点的三角形是等腰三角形 若存在,请直接写出点P的坐标;若不存在,请说明理由.
7.如图1,等腰直角△ABC中,∠ACB=90°,CB=CA,直线DE经过点C,过A作AD⊥DE于点D,过B作BE⊥DE于点E,则△BEC≌△CDA,我们称这种全等模型为“K型全等”.(不需要证明)
[模型应用]若一次函数y=kx+4(h≠0)的图象与x轴、y轴分别交于A、B两点.
(1)如图2,当k=﹣1时,若B到经过原点的直线l的距离BE的长为3,求A到直线l的距离AD的长.
(2)如图3,当k=﹣时,点M在第一象限内,若△ABM是等腰直角三角形,求点M的坐标.
(3)当k的取值变化时,点A随之在x轴上运动,将线段BA绕点B逆时针旋转90°得到BQ,当Q在第一象限落在直线y=0.5x+1上时,在x轴上求一点H,使HQ+HB的值最小,请求出H的坐标.
8.如图1,在平面直角坐标系xOy中,直线AB交y轴于点A(0,3),交x轴于点B(﹣4,0).
(1)求直线AB的函数表达式;
(2)如图2,在线段OB上有一点C(点C不与点O、点B重合),将AOC沿AC折叠,使点O落在AB上,记作点D,在BD上方,以BD为斜边作等腰直角三角形BDF,求点F的坐标;
(3)在(2)的条件下,如图3,在平面内是否存在一点E,使得以点A,B,E为顶点的三角形与ABC全等(点E不与点C重合),若存在,请直接写出满足条件的所有点E的坐标,若不存在,请说明理由.
9.如图,四边形是矩形,点A、C分别在x轴、y轴上,是绕点O顺时针旋转得到的,点D在x轴上,直线交y轴于点F,交于点H,点B的坐标为.
(1)求直线的表达式;
(2)求的面积;
(3)点M在x轴上,平面内处否存在点N,使以点D、F、M、N为顶点的四边形是矩形 若存在,请直接写出点N的坐标;若不存在,请说明理由.
10.在平面直角坐标系中,直线y=﹣3x﹣交x轴于点A,交y轴于点B,直线y=﹣x+3交x轴于点C,交y轴于点D.
(1)如图1,连接BC,求BCD的面积;
(2)如图2,在直线y=﹣x+3上存在点E,使得∠ABE=45°,求点E的坐标;
(3)如图3,在(2)的条件下,连接OE,过点E作CD的垂线交y轴于点F,点P在直线EF上,在平面中存在一点Q,使得以OE为一边,O,E,P,Q为顶点的四边形为菱形,请直接写出点Q的坐标.
11.如图,在平面直角坐标系中,一次函数的图像与x轴交于点A,一次函数的图像与x轴交于点B,与交于点C.点P是y轴上一点,点Q是直线上一点.
(1)求的面积;
(2)若点P在y轴的负半轴上,且是轴对称图形,求点P的坐标;
(3)若以P、Q、B、C为顶点的四边形是平行四边形,直接写出点Q的坐标.
12.如图,在平面直角坐标系中,正方形的边,分别在轴,轴的正半轴上,直线经过线段的中点,与轴交于点,是线段上一点,作点关于直线的对称点,连接,,.设点的坐标为.
(1)写出点B的坐标是______;
(2)当时,求点E的坐标;
(3)在点E的整个运动过程中,
①当四边形为菱形时,求点E的坐标;
②若N为平面内一点,当以B,E,F,N为顶点的四边形为矩形时,m的值为______.(请直接写出答案)
13.已知直线与x轴交于点A,直线与x轴交于点B,直线交于点C,且C点的横坐标为1.
(1)求直线的解析式.
(2)如图1,过点A作x轴的垂线,若点P为垂线上的一个动点,点,若,求此时点P的坐标.
(3)如图2,点E的坐标为,将直线绕点C逆时针旋转,使旋转后的直线刚好过点E,过点C作平行于x轴的直线,点分别为直线上的两个动点,是否存在点,使得是以M点为直角顶点的等腰直角三角形,若存在,直接写出N点的坐标;若不存在,请说明理由.
同课章节目录
