6.3.1 二项式定理 课件(共17张PPT)
文档属性
| 名称 | 6.3.1 二项式定理 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 355.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-13 17:32:21 | ||
图片预览





文档简介
(共17张PPT)
6.3.1 二项式定理
1.能用多项式法则和计数原理推导二项式定理,会用二项式定理求解二项展开式.
2.理解二项式定理,会利用定理解决与二项式有关的简单问题.
知识点一:二项式定理的推导
已知,
思考:观察以上展开式,分析其运算过程,你能发现什么规律?
根据多项式乘法法则,
项的形式:
展开式共有:
当 时,
2个(a+b)都不选b.
a2出现的次数 = 从2个(a+b)中取0个b(都取a)的组数 ,即a2只有1个
a2
ab
ba
b2
当 时,
当 时,
1个(a+b)中选a,另一个(a+b)中选b.
2个(a+b)都选b.
ab出现的次数=从2个(a+b)中取1个b的组数 ,即ab只有1个;
b2出现的次数=从2个(a+b)中取2个b的组数 ,即b2只有1个;
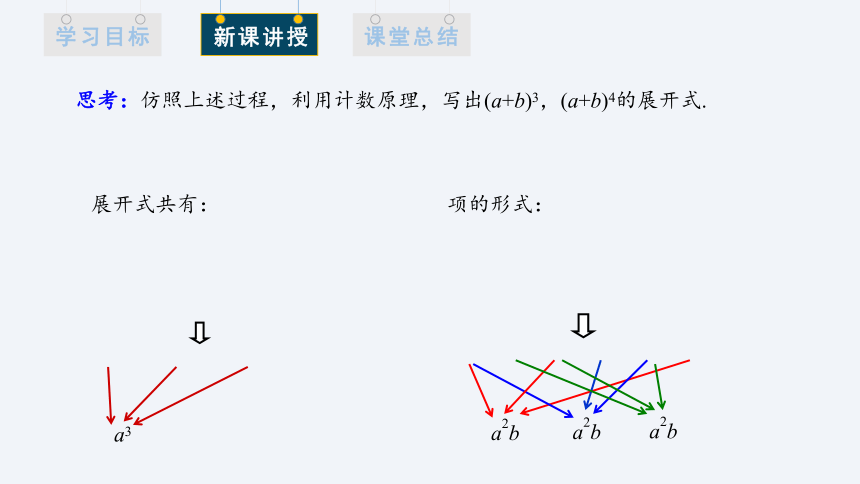
思考:仿照上述过程,利用计数原理,写出(a+b)3,(a+b)4的展开式.
展开式共有:
项的形式:
a3
a2b
a2b
a2b
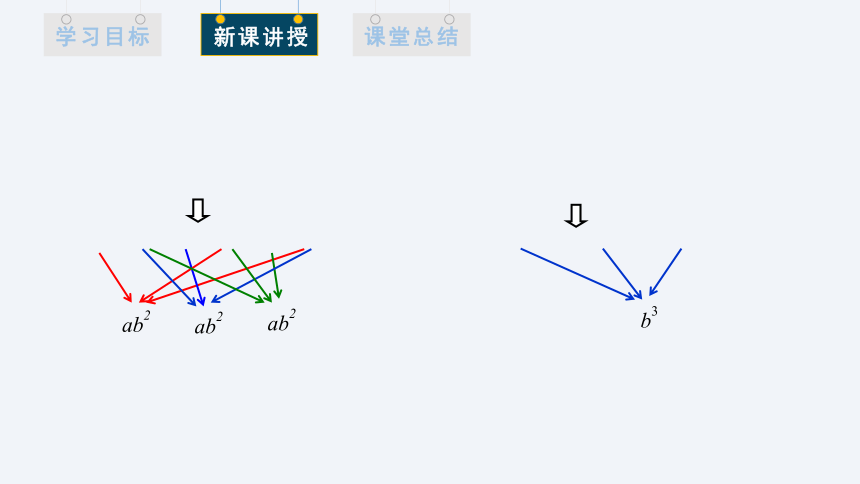
ab2
ab2
ab2
b3
a4
a3b
ab3
b4
a2b2
问题:根据以上分析,猜想(a+b)n的展开式是怎样的?
各项是从n个因式中各取一个字母相乘得到关于a,b的n次单项式,有
,共n+1项.
项的结构:
……
项的系数:
项是从n个因式中都取b,有 种.
项是从n个因式中取k个b,有 种;
项是从n个因式中取2个b,有 种;
项是从n个因式中取1个b,有 种;
项是从n个因式中都不取b,有 种;
……
概念生成
二项式定理:
(a+b)n的二项展开式
(1)展开式共有 项.
(2)各项的次数都等于二项式的次数n;
字母a按降幂排列,次数由n递减到0;字母b按升幂排列,次数由0递增到n.
n+1
注意:
(3)二项展开式中,系数 叫做二项式系数,它们依次为
(4) 叫做二项展开式的通项,用Tk+1表示,即为展开式的第k+1项
在二项式定理中,若设a=1,b=x,则得到公式
例1 求 的展开式.
解:根据二项式定理,
知识点二:二项式定理的应用
练一练
求 的展开式.
解:
例2 (1) 求(1+2x)7的展开式的第4项的系数;
(2)求 的展开式中x2的系数.
解:(1)(1+2x)7的展开式的第4项是
T3+1 =·17-3· (2x)3
=×23x3
=35× 8× x3
=280x3
因此,展开式第4项的系数是280.
(2) 的展开式的通项是
根据题意,得
3-k=2,
k=1
因此,x2的系数是
(-1)×25×=-192
注意:二项式展开式的某一项二项式系数与这一项的系数是两个不同的概念
求(x+a)12的展开式中的第10项的系数.
练一练
解:
因此,展开式第10项的系数是220.
根据今天所学,回答下列问题:
1.二项式定理是怎样的?
2.二项式系数和展开式通项分别是什么?
6.3.1 二项式定理
1.能用多项式法则和计数原理推导二项式定理,会用二项式定理求解二项展开式.
2.理解二项式定理,会利用定理解决与二项式有关的简单问题.
知识点一:二项式定理的推导
已知,
思考:观察以上展开式,分析其运算过程,你能发现什么规律?
根据多项式乘法法则,
项的形式:
展开式共有:
当 时,
2个(a+b)都不选b.
a2出现的次数 = 从2个(a+b)中取0个b(都取a)的组数 ,即a2只有1个
a2
ab
ba
b2
当 时,
当 时,
1个(a+b)中选a,另一个(a+b)中选b.
2个(a+b)都选b.
ab出现的次数=从2个(a+b)中取1个b的组数 ,即ab只有1个;
b2出现的次数=从2个(a+b)中取2个b的组数 ,即b2只有1个;
思考:仿照上述过程,利用计数原理,写出(a+b)3,(a+b)4的展开式.
展开式共有:
项的形式:
a3
a2b
a2b
a2b
ab2
ab2
ab2
b3
a4
a3b
ab3
b4
a2b2
问题:根据以上分析,猜想(a+b)n的展开式是怎样的?
各项是从n个因式中各取一个字母相乘得到关于a,b的n次单项式,有
,共n+1项.
项的结构:
……
项的系数:
项是从n个因式中都取b,有 种.
项是从n个因式中取k个b,有 种;
项是从n个因式中取2个b,有 种;
项是从n个因式中取1个b,有 种;
项是从n个因式中都不取b,有 种;
……
概念生成
二项式定理:
(a+b)n的二项展开式
(1)展开式共有 项.
(2)各项的次数都等于二项式的次数n;
字母a按降幂排列,次数由n递减到0;字母b按升幂排列,次数由0递增到n.
n+1
注意:
(3)二项展开式中,系数 叫做二项式系数,它们依次为
(4) 叫做二项展开式的通项,用Tk+1表示,即为展开式的第k+1项
在二项式定理中,若设a=1,b=x,则得到公式
例1 求 的展开式.
解:根据二项式定理,
知识点二:二项式定理的应用
练一练
求 的展开式.
解:
例2 (1) 求(1+2x)7的展开式的第4项的系数;
(2)求 的展开式中x2的系数.
解:(1)(1+2x)7的展开式的第4项是
T3+1 =·17-3· (2x)3
=×23x3
=35× 8× x3
=280x3
因此,展开式第4项的系数是280.
(2) 的展开式的通项是
根据题意,得
3-k=2,
k=1
因此,x2的系数是
(-1)×25×=-192
注意:二项式展开式的某一项二项式系数与这一项的系数是两个不同的概念
求(x+a)12的展开式中的第10项的系数.
练一练
解:
因此,展开式第10项的系数是220.
根据今天所学,回答下列问题:
1.二项式定理是怎样的?
2.二项式系数和展开式通项分别是什么?
