7.1.1 条件概率 课件(共23张PPT)
文档属性
| 名称 | 7.1.1 条件概率 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 475.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-13 17:34:28 | ||
图片预览







文档简介
(共23张PPT)
7.1.1 条件概率
1.结合古典概型,了解条件概率与概率的乘法公式,能计算简单随机事件的条件概率.
2.结合古典概型,了解条件概率与独立性的关系.
知识点一:条件概率
思考:当事件A与B相互独立时,有P(AB)=P(A)P(B);如果事件A与B不独立,如何表示积事件AB的概率呢?
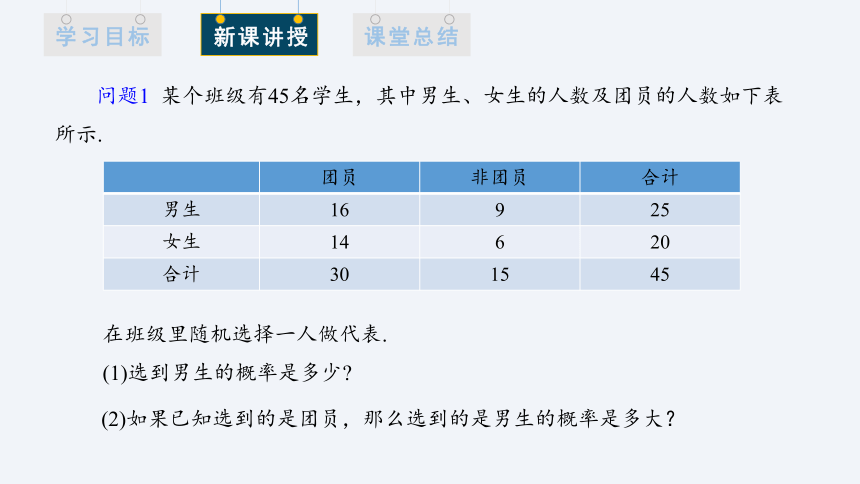
问题1 某个班级有45名学生,其中男生、女生的人数及团员的人数如下表
所示.
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(1)选到男生的概率是多少
(2)如果已知选到的是团员,那么选到的是男生的概率是多大?
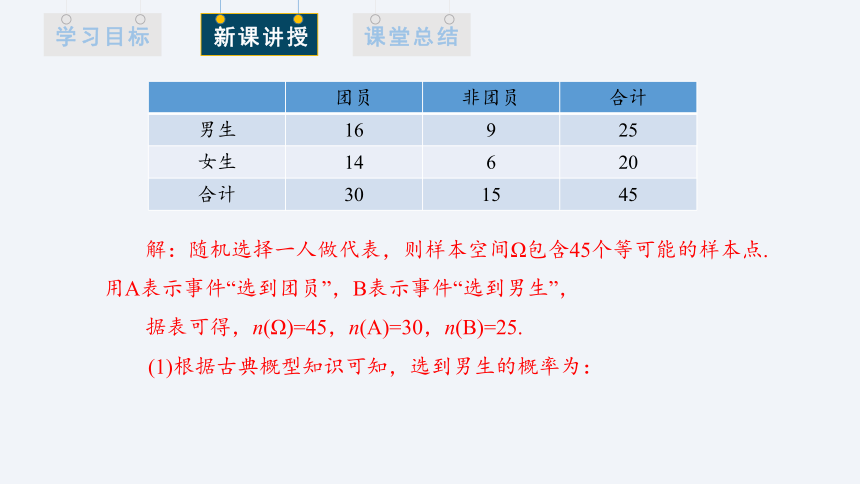
解:随机选择一人做代表,则样本空间Ω包含45个等可能的样本点.
用A表示事件“选到团员”,B表示事件“选到男生”,
据表可得,n(Ω)=45,n(A)=30,n(B)=25.
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
(1)根据古典概型知识可知,选到男生的概率为:
(2)如果已知选到的是团员,那么选到的是男生的概率是多大?
“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A).
以A为样本空间来考虑事件B发生的概率,在新的样本空间中事件B就是积事件AB,包含的样本点数n(AB)=16.
根据古典概型知识可知,
问题2 假设生男孩与生女孩是等可能的,现考虑有两个小孩的家庭,随机选择一个家庭,那么:
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率有多大?
解:用b表示男孩,g表示女孩,则样本空间Ω={bb,bg,gb,gg},且所有样本点是等可能的.
用A表示事件“选择的家庭中有女孩”,B表示事件“选择的家庭中两个孩子都是女孩”,则A={bg,gb,gg},B={gg}.
(1)根据古典概型知识可知,该家庭中两个小孩都是女孩的概率为:
(2)“在选择的家庭有女孩的条件下,两个小孩都是女孩”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A).
此时,A成为样本空间,事件B就是积事件AB.
根据古典概型知识可知:
如图所示,若已知事件A发生,则A成为样本空间.此时,事件B发生的概率是AB包含的样本点数与A包含的样本点数的比值,即这个结论对于一般的古典概型仍然成立.
A
B
AB
Ω
因为
所以,在事件A发生的条件下,事件B发生的概率还可以通过来计算.
概念生成
一般地,设A,B为两个随机事件,且P(A)>0,我们称
为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
知识点二:条件概率与独立性的关系及概率的乘法公式
问题4 在问题1和问题2中,都有P(B|A)≠P(B).一般地, P(B | A)与P(B)不一定相等.如果P(B | A)与P(B)相等,那么事件A与B应满足什么条件?
若事件A与B相互独立,即P(AB)=P(A)P(B),且P(A)>0,则
反之,若P(B | A)=P(B),且P(A)>0,则
当P(A)>0时,当且仅当事件A与B相互独立时,有P(B|A)=P(B)
思考:对于任意两个事件A与B,如果已知P(A)与P(B|A),如何计算P(AB)呢?
概念生成
由条件概率的定义,对任意两个事件A与B,若P(A)>0,则
P(AB)=P(A)P(B|A).
我们称上式为概率的乘法公式.
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
解法1:设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB.
n(Ω)==5×4=20.
因为n(AB)=
所以
(2)“在第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件B发生的概率.显然P(A)=.利用条件概率公式,得
解法2:在缩小的样本空间A上求P(B | A).已知第1次抽到代数题,这时还余下4道试题,其中代数题和几何题各2道.因此,事件A发生的条件下,事件B发生的概率为
又P(A)=,利用乘法公式可得
P(AB)=P(A)P(B|A)= = .
归纳总结
1.求条件概率有两种方法:
①基于样本空间Ω,先计算P(A)和P(AB),再利用条件概率公式求P(B|A);
②根据条件概率的直观意义,增加了“A发生”的条件后,样本空间缩小为A,求P(B|A)就是以A为样本空间计算AB的概率.
设P(A)>0,则
(1)P(Ω|A)=1;
(2)如果B,C是两个互斥事件,则P(B∪C | A)=P(B|A)+P(C|A);
(3)设和B互为对立事件,则
2.条件概率的性质:
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张.他们中奖的概率与抽奖的次序有关吗?
解:用A,B,C分别表示甲、乙、丙中奖的事件,则
因为P(A)=P(B)=P(C),所以中奖的概率与抽奖的次序无关.
.
A B C
追问:如果是放回随机抽样,中奖的概率与抽奖的次序有关吗?获奖的情况会有什么改变?
在抽奖问题中,无论是放回随机抽取还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了密码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解:(1)设Ai =”第i次按对密码”(i=1,2),则事件“不超过2次就按对密码”可表示为:,事件A1 与互斥,则
所以,任意按最后1位数字,不超过2次就按对的概率为.
(2)设B=”最后1位密码为偶数”,则
因此,如果记得密码的最后1位是偶数,不超过2次就按对的概率为.
.
练一练
在一个袋子中装有10个球,设有1个红球,2个黄球,3个黑球,4个白球,从中依次摸2个球,求在第1个球是红球的条件下,第2个球是黄球或黑球的概率.
解:设“摸出第1个球为红球”为事件A,“摸出第2个球为黄球”为事件B,
“摸出第2个球为黑球”为事件C,则
,
所以 .
则所求条件概率为.
根据今天所学,回答下列问题:
1.条件概念的概率是什么?
2.条件概率的性质有哪几条?
3.求条件概率的两种方法分别是什么?
7.1.1 条件概率
1.结合古典概型,了解条件概率与概率的乘法公式,能计算简单随机事件的条件概率.
2.结合古典概型,了解条件概率与独立性的关系.
知识点一:条件概率
思考:当事件A与B相互独立时,有P(AB)=P(A)P(B);如果事件A与B不独立,如何表示积事件AB的概率呢?
问题1 某个班级有45名学生,其中男生、女生的人数及团员的人数如下表
所示.
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(1)选到男生的概率是多少
(2)如果已知选到的是团员,那么选到的是男生的概率是多大?
解:随机选择一人做代表,则样本空间Ω包含45个等可能的样本点.
用A表示事件“选到团员”,B表示事件“选到男生”,
据表可得,n(Ω)=45,n(A)=30,n(B)=25.
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
(1)根据古典概型知识可知,选到男生的概率为:
(2)如果已知选到的是团员,那么选到的是男生的概率是多大?
“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A).
以A为样本空间来考虑事件B发生的概率,在新的样本空间中事件B就是积事件AB,包含的样本点数n(AB)=16.
根据古典概型知识可知,
问题2 假设生男孩与生女孩是等可能的,现考虑有两个小孩的家庭,随机选择一个家庭,那么:
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率有多大?
解:用b表示男孩,g表示女孩,则样本空间Ω={bb,bg,gb,gg},且所有样本点是等可能的.
用A表示事件“选择的家庭中有女孩”,B表示事件“选择的家庭中两个孩子都是女孩”,则A={bg,gb,gg},B={gg}.
(1)根据古典概型知识可知,该家庭中两个小孩都是女孩的概率为:
(2)“在选择的家庭有女孩的条件下,两个小孩都是女孩”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A).
此时,A成为样本空间,事件B就是积事件AB.
根据古典概型知识可知:
如图所示,若已知事件A发生,则A成为样本空间.此时,事件B发生的概率是AB包含的样本点数与A包含的样本点数的比值,即这个结论对于一般的古典概型仍然成立.
A
B
AB
Ω
因为
所以,在事件A发生的条件下,事件B发生的概率还可以通过来计算.
概念生成
一般地,设A,B为两个随机事件,且P(A)>0,我们称
为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
知识点二:条件概率与独立性的关系及概率的乘法公式
问题4 在问题1和问题2中,都有P(B|A)≠P(B).一般地, P(B | A)与P(B)不一定相等.如果P(B | A)与P(B)相等,那么事件A与B应满足什么条件?
若事件A与B相互独立,即P(AB)=P(A)P(B),且P(A)>0,则
反之,若P(B | A)=P(B),且P(A)>0,则
当P(A)>0时,当且仅当事件A与B相互独立时,有P(B|A)=P(B)
思考:对于任意两个事件A与B,如果已知P(A)与P(B|A),如何计算P(AB)呢?
概念生成
由条件概率的定义,对任意两个事件A与B,若P(A)>0,则
P(AB)=P(A)P(B|A).
我们称上式为概率的乘法公式.
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
解法1:设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB.
n(Ω)==5×4=20.
因为n(AB)=
所以
(2)“在第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件B发生的概率.显然P(A)=.利用条件概率公式,得
解法2:在缩小的样本空间A上求P(B | A).已知第1次抽到代数题,这时还余下4道试题,其中代数题和几何题各2道.因此,事件A发生的条件下,事件B发生的概率为
又P(A)=,利用乘法公式可得
P(AB)=P(A)P(B|A)= = .
归纳总结
1.求条件概率有两种方法:
①基于样本空间Ω,先计算P(A)和P(AB),再利用条件概率公式求P(B|A);
②根据条件概率的直观意义,增加了“A发生”的条件后,样本空间缩小为A,求P(B|A)就是以A为样本空间计算AB的概率.
设P(A)>0,则
(1)P(Ω|A)=1;
(2)如果B,C是两个互斥事件,则P(B∪C | A)=P(B|A)+P(C|A);
(3)设和B互为对立事件,则
2.条件概率的性质:
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张.他们中奖的概率与抽奖的次序有关吗?
解:用A,B,C分别表示甲、乙、丙中奖的事件,则
因为P(A)=P(B)=P(C),所以中奖的概率与抽奖的次序无关.
.
A B C
追问:如果是放回随机抽样,中奖的概率与抽奖的次序有关吗?获奖的情况会有什么改变?
在抽奖问题中,无论是放回随机抽取还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了密码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解:(1)设Ai =”第i次按对密码”(i=1,2),则事件“不超过2次就按对密码”可表示为:,事件A1 与互斥,则
所以,任意按最后1位数字,不超过2次就按对的概率为.
(2)设B=”最后1位密码为偶数”,则
因此,如果记得密码的最后1位是偶数,不超过2次就按对的概率为.
.
练一练
在一个袋子中装有10个球,设有1个红球,2个黄球,3个黑球,4个白球,从中依次摸2个球,求在第1个球是红球的条件下,第2个球是黄球或黑球的概率.
解:设“摸出第1个球为红球”为事件A,“摸出第2个球为黄球”为事件B,
“摸出第2个球为黑球”为事件C,则
,
所以 .
则所求条件概率为.
根据今天所学,回答下列问题:
1.条件概念的概率是什么?
2.条件概率的性质有哪几条?
3.求条件概率的两种方法分别是什么?
