7.1.2 全概率公式 课件(共18张PPT)
文档属性
| 名称 | 7.1.2 全概率公式 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 444.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-13 17:35:56 | ||
图片预览





文档简介
(共18张PPT)
7.1.2 全概率公式
1.结合古典概型,理解全概率公式,会利用全概率公式计算概率;
2.了解贝叶斯公式.
知识点一:全概率公式的概念
问题1 从有a个红球和b个蓝球的袋子中,每次随机摸出1个球,摸出的
球不再放回.显然,第1次摸到红球的概率为 .那么第2次摸到红球的概率
是多大?如何计算这个概率呢?
因为抽签具有公平性,所以第二次摸到红球的概率也应该是
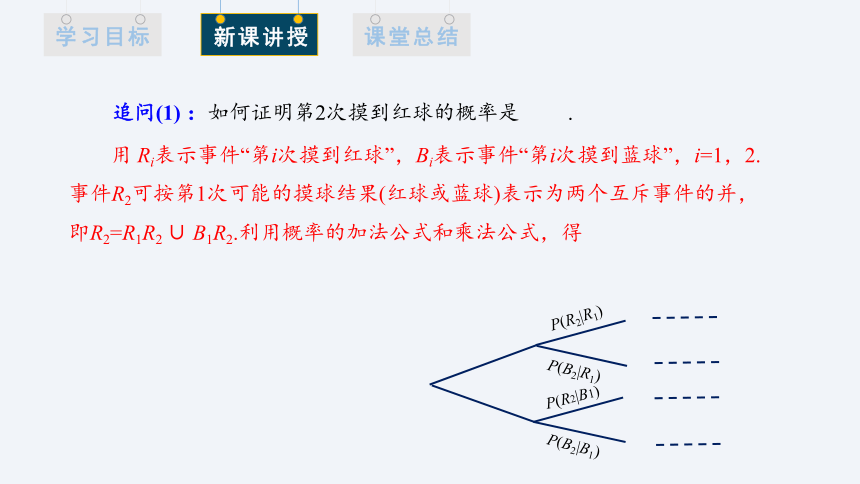
用 Ri表示事件“第i次摸到红球”,Bi表示事件“第i次摸到蓝球”,i=1,2.事件R2可按第1次可能的摸球结果(红球或蓝球)表示为两个互斥事件的并,即R2=R1R2 ∪ B1R2.利用概率的加法公式和乘法公式,得
P(R2|R1)
P(B2|R1)
P(R2|B1)
P(B2|B1)
追问(1) :如何证明第2次摸到红球的概率是 .
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
追问(2):将以上问题一般化,你能得到什么结果?
设A1,A2,...,An是一组两两互斥的事件,A1∪A2∪...∪An=Ω,且P(Ai)>0,i=1,2,...,n,则对任意的事件,求事件B的概率P(B).
上述过程采用的方法:
概念生成
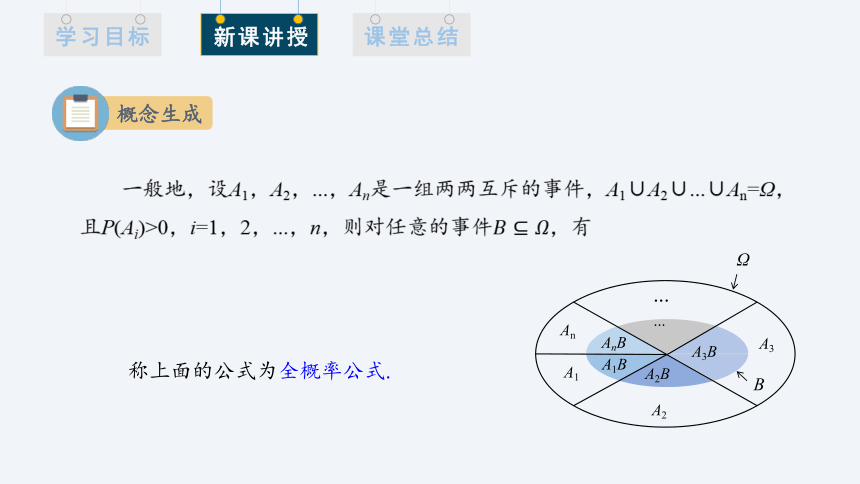
一般地,设A1,A2,...,An是一组两两互斥的事件,A1∪A2∪...∪An=Ω,
且P(Ai)>0,i=1,2,...,n,则对任意的事件,有
称上面的公式为全概率公式.
A1
A1B
A2
A2B
A3B
A3
An
AnB
...
...
Ω
B
例1 某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8,计算王同学第2天去A餐厅用餐的概率.
解:设A1=“第1天去A餐厅用餐”, B1=“第1天去B餐厅用餐”, A2=“第2天去A餐厅用餐”,则Ω=A1∪B1,且A1与B1互斥,根据题意得
P(A2)= P(A1) P(A2| A1)+ P(B1) P(A2| B1)
=0.5×0.6+0.5 ×0.8=0.7
因此,王同学第2天去A餐厅用餐的概率为0.7.
由全概率公式,得
P(A1)=P(B1)=0.5, P(A2| A1)=0.6, P(A2| B1)=0.8.
知识点二:全概率公式的运用
P(A2|A1)=( )
P(A2|B1)=( )
归纳总结
运用全概率公式求概率的解题步骤:
(1)用符号表示随机事件;
(2)划分样本空间;
(3)分别计算概率;
(4)由全概率公式求出概率.
例2 有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
(2)如果取到的零件是次品,计算它是第i (i=1,2,3)台车床加工的概率.
解:设B=“任取一个零件为次品”,Ai=“零件为第i台车床加工”(i=1,2,3),
则Ω= A1∪A2∪A3,且A1,A2,A3两两互斥.
A1
A2
A3
A3B
A1B
A2B
Ω
B
P (A1)=0.25, P (A2)=0.3, P (A3)=0.45,
P (B|A1)=0.06, P (B|A2)= P (B|A3)=0.05.
根据题意得:
(1)由全概率公式,得
P(B)=P(A1) P (B|A1)+ P(A2) P (B|A2)+ P(A3)P (B|A3)
=0.25×0.06+0.3×0.05+0.45×0.05
=0.0525
(2)“如果取到的零件是次品,计算它是第i( i =1,2,3)台车床加工的概率”,就是计算在B发生的条件下,事件Ai发生的概率.
同理可得
; .
问题2:在上面的例题解答中,概率P(Ai),P(Ai|B)的实际意义是什么?你能梳理出解决问题(2)过程中的关键等式吗?
P(Ai)是试验之前就已知的概率,它是第i台车床加工的零件所占的比例,称为先验概率.当已知抽到的零件是次品(B发生),P(Ai│B)是这件次品来自第i台车床加工的可能性大小,通常称为后验概率.
如果对加工的次品,要求操作员承担相应的责任,那么,,就分别是第1,2,3台车床操作员应承担的份额.
解决问题的关键等式:
概念生成
贝叶斯公式:设A1,A2,...,An是一组两两互斥的事件,A1∪A2∪...∪An=Ω,
且P(Ai)>0,i=1,2,...,n,则对任意的事件B Ω,P(B)>0,有
注意:贝叶斯公式一般适用于已知事件的结果,求某一种情况发生的概率.
例3 在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干
扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为
0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和
0.05.假设发送信号0和1是等可能的.
(1)分别求接收的信号为0和1的概率;
(2)已知接收的信号为0,求发送的信号是1的概率.
发送0(A)
发送1()
接收0(B)
接收1()
解:设A=“发送的信号为0”,B=“接收到的信号为0”,则=“发送的信号为1”,=“接收到的信号为1”.由题意得
练一练
同一种产品由甲、乙、丙三个厂供应.由长期的经验知,三家的正品率分别为0.95,0.90,0.80,三家产品数按2∶3∶5的比例混合在一起.
(1)从中任取一件,求此产品为正品的概率;
(2)现取到一件产品为正品,问它是由甲、乙、丙三个厂中哪个厂生产的可能性大?
=0.2×0.95+0.3×0.9+0.5×0.8=0.86,
(1)由全概率公式得:
解:设事件A表示“取到的产品为正品”,B1,B2,B3分别表示“产品由甲、乙、丙厂生产”,由已知P(B1)=0.2,P(B2)=0.3,P(B3)=0.5,
P(A|B1)=0.95,P(A|B2)=0.9,P(A|B3)=0.8,
(2)由贝叶斯公式得
由以上3个数作比较,可知这件产品由丙厂生产的可能性最大,由甲厂生产的可能性最小.
根据今天所学,回答下列问题:
1.全概率公式中将样本空间拆分成若干个两两互斥事件的作用是什么?
2.应用全概率公式的步骤是什么?
7.1.2 全概率公式
1.结合古典概型,理解全概率公式,会利用全概率公式计算概率;
2.了解贝叶斯公式.
知识点一:全概率公式的概念
问题1 从有a个红球和b个蓝球的袋子中,每次随机摸出1个球,摸出的
球不再放回.显然,第1次摸到红球的概率为 .那么第2次摸到红球的概率
是多大?如何计算这个概率呢?
因为抽签具有公平性,所以第二次摸到红球的概率也应该是
用 Ri表示事件“第i次摸到红球”,Bi表示事件“第i次摸到蓝球”,i=1,2.事件R2可按第1次可能的摸球结果(红球或蓝球)表示为两个互斥事件的并,即R2=R1R2 ∪ B1R2.利用概率的加法公式和乘法公式,得
P(R2|R1)
P(B2|R1)
P(R2|B1)
P(B2|B1)
追问(1) :如何证明第2次摸到红球的概率是 .
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
追问(2):将以上问题一般化,你能得到什么结果?
设A1,A2,...,An是一组两两互斥的事件,A1∪A2∪...∪An=Ω,且P(Ai)>0,i=1,2,...,n,则对任意的事件,求事件B的概率P(B).
上述过程采用的方法:
概念生成
一般地,设A1,A2,...,An是一组两两互斥的事件,A1∪A2∪...∪An=Ω,
且P(Ai)>0,i=1,2,...,n,则对任意的事件,有
称上面的公式为全概率公式.
A1
A1B
A2
A2B
A3B
A3
An
AnB
...
...
Ω
B
例1 某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8,计算王同学第2天去A餐厅用餐的概率.
解:设A1=“第1天去A餐厅用餐”, B1=“第1天去B餐厅用餐”, A2=“第2天去A餐厅用餐”,则Ω=A1∪B1,且A1与B1互斥,根据题意得
P(A2)= P(A1) P(A2| A1)+ P(B1) P(A2| B1)
=0.5×0.6+0.5 ×0.8=0.7
因此,王同学第2天去A餐厅用餐的概率为0.7.
由全概率公式,得
P(A1)=P(B1)=0.5, P(A2| A1)=0.6, P(A2| B1)=0.8.
知识点二:全概率公式的运用
P(A2|A1)=( )
P(A2|B1)=( )
归纳总结
运用全概率公式求概率的解题步骤:
(1)用符号表示随机事件;
(2)划分样本空间;
(3)分别计算概率;
(4)由全概率公式求出概率.
例2 有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
(2)如果取到的零件是次品,计算它是第i (i=1,2,3)台车床加工的概率.
解:设B=“任取一个零件为次品”,Ai=“零件为第i台车床加工”(i=1,2,3),
则Ω= A1∪A2∪A3,且A1,A2,A3两两互斥.
A1
A2
A3
A3B
A1B
A2B
Ω
B
P (A1)=0.25, P (A2)=0.3, P (A3)=0.45,
P (B|A1)=0.06, P (B|A2)= P (B|A3)=0.05.
根据题意得:
(1)由全概率公式,得
P(B)=P(A1) P (B|A1)+ P(A2) P (B|A2)+ P(A3)P (B|A3)
=0.25×0.06+0.3×0.05+0.45×0.05
=0.0525
(2)“如果取到的零件是次品,计算它是第i( i =1,2,3)台车床加工的概率”,就是计算在B发生的条件下,事件Ai发生的概率.
同理可得
; .
问题2:在上面的例题解答中,概率P(Ai),P(Ai|B)的实际意义是什么?你能梳理出解决问题(2)过程中的关键等式吗?
P(Ai)是试验之前就已知的概率,它是第i台车床加工的零件所占的比例,称为先验概率.当已知抽到的零件是次品(B发生),P(Ai│B)是这件次品来自第i台车床加工的可能性大小,通常称为后验概率.
如果对加工的次品,要求操作员承担相应的责任,那么,,就分别是第1,2,3台车床操作员应承担的份额.
解决问题的关键等式:
概念生成
贝叶斯公式:设A1,A2,...,An是一组两两互斥的事件,A1∪A2∪...∪An=Ω,
且P(Ai)>0,i=1,2,...,n,则对任意的事件B Ω,P(B)>0,有
注意:贝叶斯公式一般适用于已知事件的结果,求某一种情况发生的概率.
例3 在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干
扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为
0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和
0.05.假设发送信号0和1是等可能的.
(1)分别求接收的信号为0和1的概率;
(2)已知接收的信号为0,求发送的信号是1的概率.
发送0(A)
发送1()
接收0(B)
接收1()
解:设A=“发送的信号为0”,B=“接收到的信号为0”,则=“发送的信号为1”,=“接收到的信号为1”.由题意得
练一练
同一种产品由甲、乙、丙三个厂供应.由长期的经验知,三家的正品率分别为0.95,0.90,0.80,三家产品数按2∶3∶5的比例混合在一起.
(1)从中任取一件,求此产品为正品的概率;
(2)现取到一件产品为正品,问它是由甲、乙、丙三个厂中哪个厂生产的可能性大?
=0.2×0.95+0.3×0.9+0.5×0.8=0.86,
(1)由全概率公式得:
解:设事件A表示“取到的产品为正品”,B1,B2,B3分别表示“产品由甲、乙、丙厂生产”,由已知P(B1)=0.2,P(B2)=0.3,P(B3)=0.5,
P(A|B1)=0.95,P(A|B2)=0.9,P(A|B3)=0.8,
(2)由贝叶斯公式得
由以上3个数作比较,可知这件产品由丙厂生产的可能性最大,由甲厂生产的可能性最小.
根据今天所学,回答下列问题:
1.全概率公式中将样本空间拆分成若干个两两互斥事件的作用是什么?
2.应用全概率公式的步骤是什么?
