8.1.2 样本相关系数 课件(共23张PPT)
文档属性
| 名称 | 8.1.2 样本相关系数 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-13 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
8.1.2 样本相关系数
1. 结合实例,了解样本相关系数的统计含义,了解样本相关系数与“标准化”处理后的成对数据两分量向量夹角的关系;
2. 结合实例,会通过相关系数比较多组成对数据的相关性.
散点图
变量相关关系
定性推断
思考:如何对成对样本数据的相关程度进行定量分析
成对样本数据为(x1,y1),(x2,y2),…,(xn,yn),
其中
问题1:如何引入一个恰当的“数字特征”,对成对样本数据的相关程度进行定量分析?
知识点一:样本相关系数
将数据以(,)为零点进行平移,得到平移后的成对数据为
并绘制散点图.
年龄/岁
脂肪含量/%
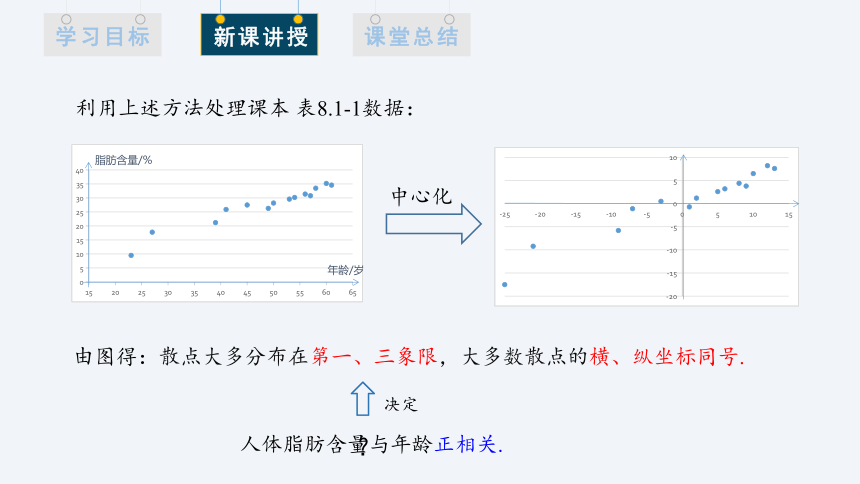
中心化
利用上述方法处理课本 表8.1-1数据:
由图得:散点大多分布在第一、三象限,大多数散点的横、纵坐标同号.
人体脂肪含量与年龄正相关.
决定
?
如果变量x,y正相关,
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
如果变量x,y负相关,
那么关于均值平移后的大多数点将分布在第一、三象限,对应的成对数据同号居多;
那么关于均值平移后的大多数点将分布在第二、四象限,对应的成对数据异号居多.
根据散点图特征,初步构造统计量
利用散点 的横纵坐标是否同号,可以构造一个量
一般情况下, 表明成对样本数据正相关;
表明成对样本数据负相关;
思考:你认为Lxy的大小一定能度量出成对样本数据的相关程度吗?
因为Lxy的大小与数据的度量单位有关,所以不能直接用它度量成对样本数据相关程度的大小.
在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高单位
由米改为厘米,得:
但单位的改变并不会改变体重与身高之间的相关程度.
为了消除单位的影响,进一步做“标准化”处理
记为
我们称r为变量x和变量y的样本相关系数.
当r>0时,称成对样本数据正相关;
当r<0时,称成对样本数据负相关.
样本相关系数r是一个描述成对样本数据的数字特征,它的正负和绝对值的大小可以反映成对样本数据的变化特征:
概念生成
问题3:样本相关系数r的大小与成对样本数据的相关程度有什么内在联系呢?
标准化处理后的成对样本数据:
设其第一分量为
设其第二分量为
同理可得:
追问1:当|r|=1时,成对样本数据之间具有怎样的关系?
r = cos θ,当|r|=1时,θ=0或π,向量 与 共线.
即存在实数λ,使得
即成对样本数据(xi,yi)都落在直线 上.
此时成对样本数据的两个分量之间满足一种线性关系.
由此可见,样本相关系数r的取值范围为[-1,1],样本相关系数r的绝对值大小可以反映成对样本数据之间线性相关的程度:
当|r|越接近1时,成对样本数据的线性相关程度越强;
当|r|越接近0时,成对样本数据的线性相关程度越弱.
样本相关系数r有时也称样本线性相关系数,|r|刻画了样本点集中于某条直线的程度.当r=0时,只表明成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系.
注意:
两个随机变量的相关性可以通过散点图对成对样本数据进行分析,而样本相关系数r可以反映两个随机变量之间的线性相关程度:
r的符号反映相关关系的正负性,|r|的大小反映两个变量线性相关的程度,即散点集中于一条直线的程度.
例1 根据下表中脂肪含量和年龄的样本数据,画出散点图,判断成对样本数据是否线性相关,并通过样本相关系数判断年龄和脂肪的相关程度和变化趋势的异同?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
参考数据:
解:先画出散点图,如图所示:
观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
参考数据:
由样本相关系数r ≈ 0.97 ,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
解:
例2 有人收集了某城市居民收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示.
第n年 1 2 3 4 5 6 7 8 9 10
居民年收入/亿元 32.2 31.1 32.9 35.8 37.1 38 39 43 44.6 46
A商品销售额/万元 25.0 30.0 34.0 37.0 39.0 41.0 42.0 44.0 48.0 51.0
画出散点图,判断成对样本数据是否线性相关,并通过样本相关系数推断居民年收入与A商品销售额的相关程度和变化趋势的异同.
从散点图看,A商品销售额与居民年收入的样本数据呈现线性相关关系.
由此可以推断,A商品销售额与居民年收人正线性相关,即A商品销售额与居民年收入有相同的变化趋势,且相关程度很强.
得:
例3 在某校高一年级中随机抽取25名男生,测得他们的身高、体重、臂展等数据,如下表所示.
体重与身高、臂展与身高分别具有怎样的相关性
解:根据样本数据分别画出散点图.如图,两个散点图都呈现线性相关的特征:
通过计算得到体重与身高、臂展与身高的样本相关系数分别约为0.34和0.78,
都为正相关.其中,臂展与身高的相关程度更高.
成对样本数据
样本相关系数
变量相关关系
定量推断
框图结构
8.1.2 样本相关系数
1. 结合实例,了解样本相关系数的统计含义,了解样本相关系数与“标准化”处理后的成对数据两分量向量夹角的关系;
2. 结合实例,会通过相关系数比较多组成对数据的相关性.
散点图
变量相关关系
定性推断
思考:如何对成对样本数据的相关程度进行定量分析
成对样本数据为(x1,y1),(x2,y2),…,(xn,yn),
其中
问题1:如何引入一个恰当的“数字特征”,对成对样本数据的相关程度进行定量分析?
知识点一:样本相关系数
将数据以(,)为零点进行平移,得到平移后的成对数据为
并绘制散点图.
年龄/岁
脂肪含量/%
中心化
利用上述方法处理课本 表8.1-1数据:
由图得:散点大多分布在第一、三象限,大多数散点的横、纵坐标同号.
人体脂肪含量与年龄正相关.
决定
?
如果变量x,y正相关,
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
如果变量x,y负相关,
那么关于均值平移后的大多数点将分布在第一、三象限,对应的成对数据同号居多;
那么关于均值平移后的大多数点将分布在第二、四象限,对应的成对数据异号居多.
根据散点图特征,初步构造统计量
利用散点 的横纵坐标是否同号,可以构造一个量
一般情况下, 表明成对样本数据正相关;
表明成对样本数据负相关;
思考:你认为Lxy的大小一定能度量出成对样本数据的相关程度吗?
因为Lxy的大小与数据的度量单位有关,所以不能直接用它度量成对样本数据相关程度的大小.
在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高单位
由米改为厘米,得:
但单位的改变并不会改变体重与身高之间的相关程度.
为了消除单位的影响,进一步做“标准化”处理
记为
我们称r为变量x和变量y的样本相关系数.
当r>0时,称成对样本数据正相关;
当r<0时,称成对样本数据负相关.
样本相关系数r是一个描述成对样本数据的数字特征,它的正负和绝对值的大小可以反映成对样本数据的变化特征:
概念生成
问题3:样本相关系数r的大小与成对样本数据的相关程度有什么内在联系呢?
标准化处理后的成对样本数据:
设其第一分量为
设其第二分量为
同理可得:
追问1:当|r|=1时,成对样本数据之间具有怎样的关系?
r = cos θ,当|r|=1时,θ=0或π,向量 与 共线.
即存在实数λ,使得
即成对样本数据(xi,yi)都落在直线 上.
此时成对样本数据的两个分量之间满足一种线性关系.
由此可见,样本相关系数r的取值范围为[-1,1],样本相关系数r的绝对值大小可以反映成对样本数据之间线性相关的程度:
当|r|越接近1时,成对样本数据的线性相关程度越强;
当|r|越接近0时,成对样本数据的线性相关程度越弱.
样本相关系数r有时也称样本线性相关系数,|r|刻画了样本点集中于某条直线的程度.当r=0时,只表明成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系.
注意:
两个随机变量的相关性可以通过散点图对成对样本数据进行分析,而样本相关系数r可以反映两个随机变量之间的线性相关程度:
r的符号反映相关关系的正负性,|r|的大小反映两个变量线性相关的程度,即散点集中于一条直线的程度.
例1 根据下表中脂肪含量和年龄的样本数据,画出散点图,判断成对样本数据是否线性相关,并通过样本相关系数判断年龄和脂肪的相关程度和变化趋势的异同?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
参考数据:
解:先画出散点图,如图所示:
观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
参考数据:
由样本相关系数r ≈ 0.97 ,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
解:
例2 有人收集了某城市居民收入(所有居民在一年内收入的总和)与A商品销售额的10年数据,如下表所示.
第n年 1 2 3 4 5 6 7 8 9 10
居民年收入/亿元 32.2 31.1 32.9 35.8 37.1 38 39 43 44.6 46
A商品销售额/万元 25.0 30.0 34.0 37.0 39.0 41.0 42.0 44.0 48.0 51.0
画出散点图,判断成对样本数据是否线性相关,并通过样本相关系数推断居民年收入与A商品销售额的相关程度和变化趋势的异同.
从散点图看,A商品销售额与居民年收入的样本数据呈现线性相关关系.
由此可以推断,A商品销售额与居民年收人正线性相关,即A商品销售额与居民年收入有相同的变化趋势,且相关程度很强.
得:
例3 在某校高一年级中随机抽取25名男生,测得他们的身高、体重、臂展等数据,如下表所示.
体重与身高、臂展与身高分别具有怎样的相关性
解:根据样本数据分别画出散点图.如图,两个散点图都呈现线性相关的特征:
通过计算得到体重与身高、臂展与身高的样本相关系数分别约为0.34和0.78,
都为正相关.其中,臂展与身高的相关程度更高.
成对样本数据
样本相关系数
变量相关关系
定量推断
框图结构
