8.2.1 一元线性回归模型 课件(共23张PPT)
文档属性
| 名称 | 8.2.1 一元线性回归模型 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 689.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-13 17:43:16 | ||
图片预览






文档简介
(共14张PPT)
8.2.1 一元线性回归模型
1.结合具体实例,了解一元线性回归模型的含义,了解模型参数的统计意义.
回顾:根据成对样本数据的散点图和相关系数,可以得到两个变量之间的哪些信息?
思考:是否可以通过建立适当的统计模型来刻画两个变量之间的相关关系?
Y
x
统计模型
情境:生活经验告诉我们,儿子的身高与父亲的身高相关.一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如表所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
由这组样本数据能否推断儿子的身高与父亲的身高有关系?关系的相关程度如何?为什么?
知识点一:一元线性回归模型
从图上看,散点大致分布在一条直线附近.
由散点图的分布趋势表明儿子的身高与父亲的身高线性相关.
画出散点图:
利用统计软件求得相关系数r =0.886,
表明儿子的身高与父亲的身高正线性相关,
且相关程度较高.
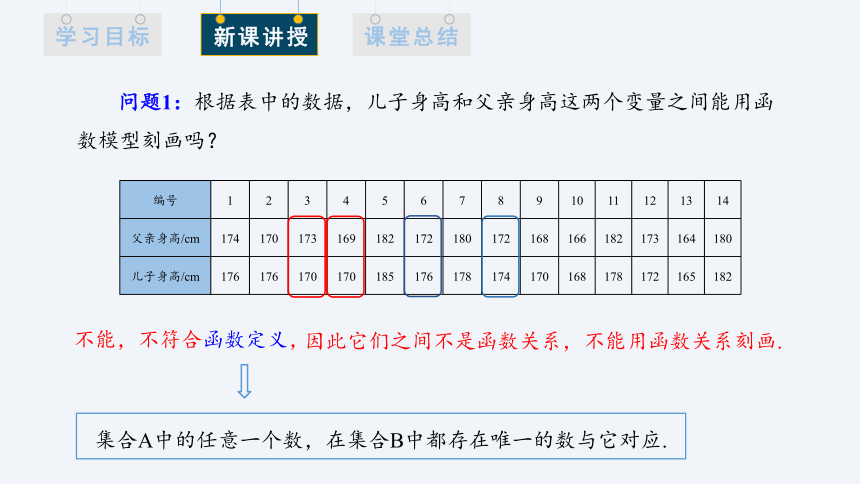
问题1:根据表中的数据,儿子身高和父亲身高这两个变量之间能用函数模型刻画吗?
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
不能,不符合函数定义,
集合A中的任意一个数,在集合B中都存在唯一的数与它对应.
因此它们之间不是函数关系,不能用函数关系刻画.
问题2:由于其他因素的存在,使得儿子身高和父亲身高有关系但不是函数关系,那么影响儿子身高的其他因素是什么?
母亲的身高
生活的环境
饮食习惯
...
营养水平
体育锻炼
如果用x表示父亲身高,Y表示儿子的身高,用e表示各种其它随机因素影响之和,称e为随机误差, 由于儿子身高与父亲身高线性相关,所以Y≈bx+a.
假设:①随机误差e的均值为0;
Y=bx+a+e
建立模型
②方差为与父亲身高无关的定值σ2.
思考:为什么要假设E(e)=0,而不假设其为某个不为0的常数?
因为误差是随机的,即取各种正负误差的可能性一样,所以它们均值的理想状态应该为0.
如果随机误差是一个不为0的常数e,则可以将 e 合并到截距项a中,否则模型无法确定,即参数没有唯一解.
如果随机误差e=0,那么Y与x之间的关系就可用一元线性函数模型来描述.
问题3:请根据以上的分析,你能建立一个数学模型表示儿子身高与父亲身高的关系吗?
我们称①式为Y关于x的一元线性回归模型,其中,Y称为因变量或响应变量,x称为自变量或解释变量. a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差.
①
如果用x表示父亲身高,Y表示儿子的身高,e表示随机误差.假定随机误差e的均值为0,方差为与父亲身高无关的定值σ2,则它们之间的关系可以表示为
概念生成
一元线性回归模型 Y=bx+a+e增加了随机误差项e,因变量 Y 的值由自变量 x和随机误差项e共同确定,即自变量x只能解释部分Y的变化.
解释变量x (身高)
模型误差e (其它所有变量)
响应变量Y(体重)
函数模型:
回归模型:
函数模型与回归模型之间的差别:
问题4:你能结合父亲与儿子身高的实例,说明回归模型①的意义
①
父亲身高为xi 的所有男大学生身高组成一个子总体,该子总体的均值为bx+a,即该子总体的均值与父亲的身高是线性函数关系.
而对于父亲身高为xi的某一名男大学生,他的身高 yi 并不一定为bxi+a,
它仅是该子总体的一个观测值,这个观测值与均值有一个误差项 ei=yi-(bxi+a).
(1)除父亲身高外,其他可能影响儿子身高的因素,比如母亲身高、生活环境、饮食习惯和锻炼时间等.
(2)在测量儿子身高时,由于测量工具、测量精度所产生的测量误差.
(3)实际问题中,我们不知道儿子身高和父亲身高的相关关系是什么,可以利用一元线性回归模型来近似这种关系,这种近似关系也是产生随机误差e的原因.
产生随机误差e的原因有:
问题5:你能结合具体实例解释产生模型①中随机误差项的原因吗
根据今天所学,回答下列问题:
1.写出一元线性回归模型,并说说其各参数分别表示什么?
2. 函数模型与一元线性回归模型之间的差别在哪?
8.2.1 一元线性回归模型
1.结合具体实例,了解一元线性回归模型的含义,了解模型参数的统计意义.
回顾:根据成对样本数据的散点图和相关系数,可以得到两个变量之间的哪些信息?
思考:是否可以通过建立适当的统计模型来刻画两个变量之间的相关关系?
Y
x
统计模型
情境:生活经验告诉我们,儿子的身高与父亲的身高相关.一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如表所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
由这组样本数据能否推断儿子的身高与父亲的身高有关系?关系的相关程度如何?为什么?
知识点一:一元线性回归模型
从图上看,散点大致分布在一条直线附近.
由散点图的分布趋势表明儿子的身高与父亲的身高线性相关.
画出散点图:
利用统计软件求得相关系数r =0.886,
表明儿子的身高与父亲的身高正线性相关,
且相关程度较高.
问题1:根据表中的数据,儿子身高和父亲身高这两个变量之间能用函数模型刻画吗?
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
不能,不符合函数定义,
集合A中的任意一个数,在集合B中都存在唯一的数与它对应.
因此它们之间不是函数关系,不能用函数关系刻画.
问题2:由于其他因素的存在,使得儿子身高和父亲身高有关系但不是函数关系,那么影响儿子身高的其他因素是什么?
母亲的身高
生活的环境
饮食习惯
...
营养水平
体育锻炼
如果用x表示父亲身高,Y表示儿子的身高,用e表示各种其它随机因素影响之和,称e为随机误差, 由于儿子身高与父亲身高线性相关,所以Y≈bx+a.
假设:①随机误差e的均值为0;
Y=bx+a+e
建立模型
②方差为与父亲身高无关的定值σ2.
思考:为什么要假设E(e)=0,而不假设其为某个不为0的常数?
因为误差是随机的,即取各种正负误差的可能性一样,所以它们均值的理想状态应该为0.
如果随机误差是一个不为0的常数e,则可以将 e 合并到截距项a中,否则模型无法确定,即参数没有唯一解.
如果随机误差e=0,那么Y与x之间的关系就可用一元线性函数模型来描述.
问题3:请根据以上的分析,你能建立一个数学模型表示儿子身高与父亲身高的关系吗?
我们称①式为Y关于x的一元线性回归模型,其中,Y称为因变量或响应变量,x称为自变量或解释变量. a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差.
①
如果用x表示父亲身高,Y表示儿子的身高,e表示随机误差.假定随机误差e的均值为0,方差为与父亲身高无关的定值σ2,则它们之间的关系可以表示为
概念生成
一元线性回归模型 Y=bx+a+e增加了随机误差项e,因变量 Y 的值由自变量 x和随机误差项e共同确定,即自变量x只能解释部分Y的变化.
解释变量x (身高)
模型误差e (其它所有变量)
响应变量Y(体重)
函数模型:
回归模型:
函数模型与回归模型之间的差别:
问题4:你能结合父亲与儿子身高的实例,说明回归模型①的意义
①
父亲身高为xi 的所有男大学生身高组成一个子总体,该子总体的均值为bx+a,即该子总体的均值与父亲的身高是线性函数关系.
而对于父亲身高为xi的某一名男大学生,他的身高 yi 并不一定为bxi+a,
它仅是该子总体的一个观测值,这个观测值与均值有一个误差项 ei=yi-(bxi+a).
(1)除父亲身高外,其他可能影响儿子身高的因素,比如母亲身高、生活环境、饮食习惯和锻炼时间等.
(2)在测量儿子身高时,由于测量工具、测量精度所产生的测量误差.
(3)实际问题中,我们不知道儿子身高和父亲身高的相关关系是什么,可以利用一元线性回归模型来近似这种关系,这种近似关系也是产生随机误差e的原因.
产生随机误差e的原因有:
问题5:你能结合具体实例解释产生模型①中随机误差项的原因吗
根据今天所学,回答下列问题:
1.写出一元线性回归模型,并说说其各参数分别表示什么?
2. 函数模型与一元线性回归模型之间的差别在哪?
