期末易错精选题练习-2023-2024学年数学八年级上册人教版(含解析)
文档属性
| 名称 | 期末易错精选题练习-2023-2024学年数学八年级上册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 13:56:37 | ||
图片预览


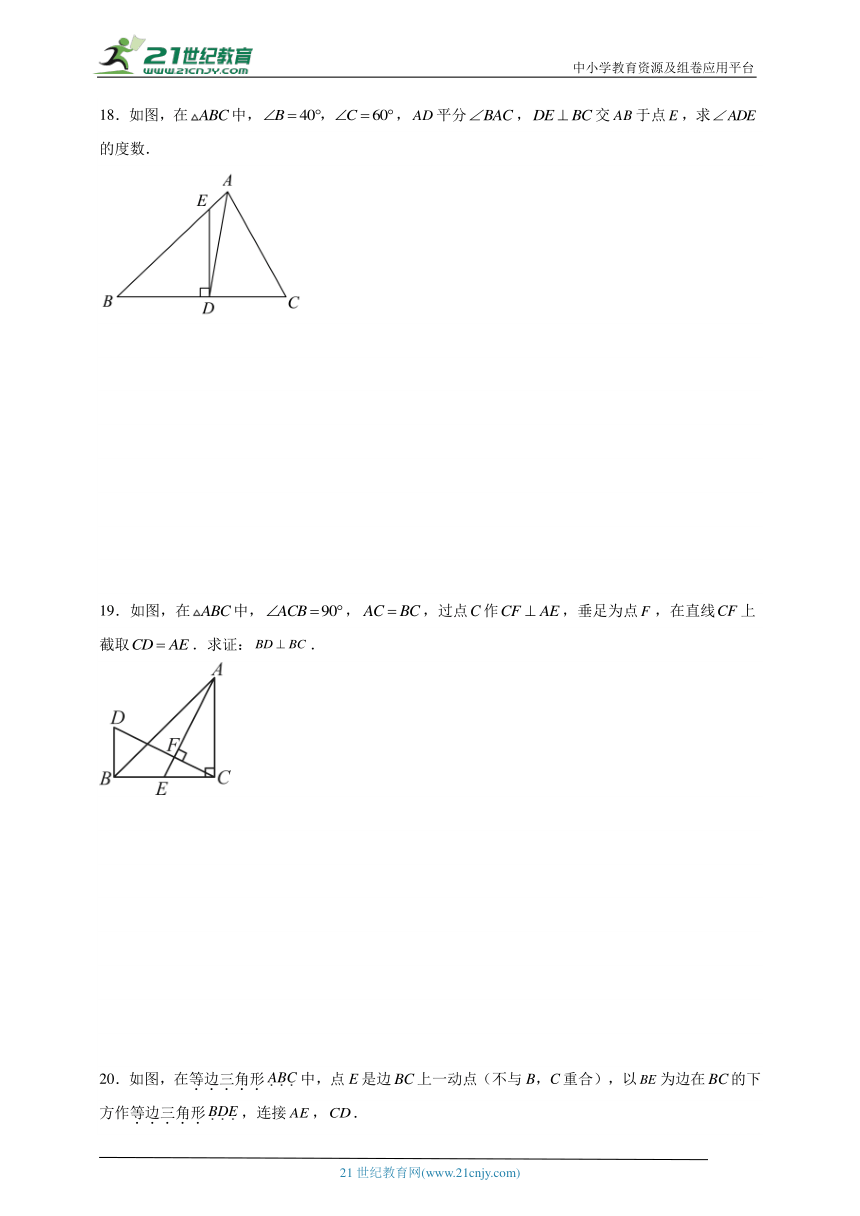

文档简介
中小学教育资源及组卷应用平台
期末易错精选题练习-2023-2024学年数学八年级上册人教版
一、单选题
1.如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
A. B. C. D.
2.过八边形的一个顶点最多可以引对角线的条数为( )
A.3 B.4 C.5 D.6
3.下列三角形一定为直角三角形的是( )
①三角形的三边之比为;②的三个内角的关系为;③三角形的三个内角之比为;④三角形的一个外角与它不相邻的两个内角和为.
A.1个 B.2个 C.3个 D.4个
4.下列各式从左到右的变形中,是因式分解的为( )
A. B.
C. D.
5.分式方程约去分母得( )
A. B.
C. D.
6.如图,在四边形中,,平分,,,,则四边形的面积是( )
A. B. C. D.
7.若,则,分别为( )
A., B., C., D.,
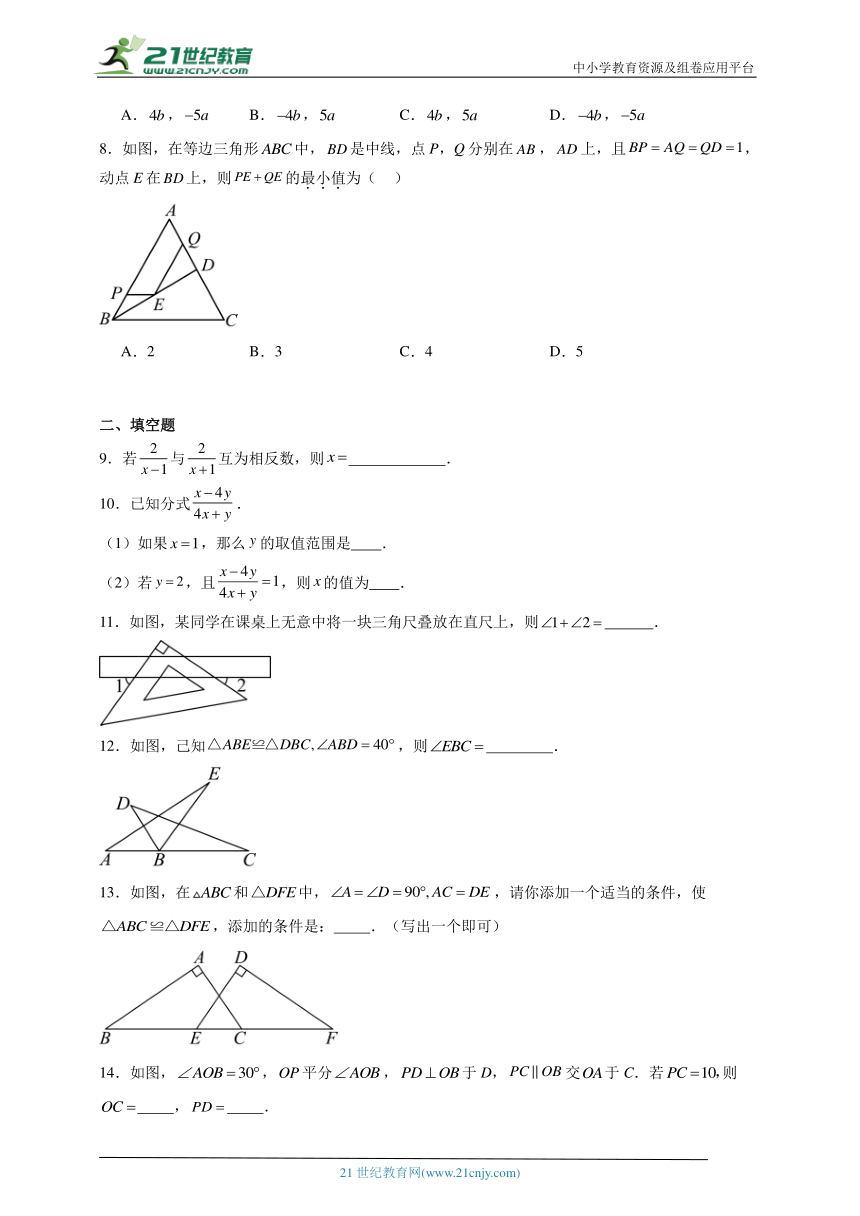
8.如图,在等边三角形中,是中线,点P,Q分别在,上,且,动点E在上,则的最小值为( )
A.2 B.3 C.4 D.5
二、填空题
9.若与互为相反数,则 .
10.已知分式.
(1)如果,那么的取值范围是 .
(2)若,且,则的值为 .
11.如图,某同学在课桌上无意中将一块三角尺叠放在直尺上,则 .
12.如图,己知,则 .
13.如图,在和中,,请你添加一个适当的条件,使,添加的条件是: .(写出一个即可)
14.如图,,平分,于D,交于C.若则 , .
15.如图,六边形是轴对称图形,所在的直线是它的对称轴.若,则的大小是 .
16.如图,杨老师在《制作长方体纸盒的活动》这一课中,把一张长方形纸板的四周各剪去一个同样大小的小正方形,然后将四周突出部分折起,制成一个长方体形状的无盖纸盒 如图所示,长方形纸板的长为,宽为,小正方形的边长为1.该无盖纸盒的底面积为 用含,的式子表示
三、解答题
17.先化简,再求值:,其中.
18.如图,在中,,平分,交于点,求的度数.
19.如图,在中,,,过点作,垂足为点,在直线上截取.求证:.
20.如图,在等边三角形中,点E是边上一动点(不与B,C重合),以为边在的下方作等边三角形,连接,.
(1)在运动的过程中,与有何数量关系?请说明理由.
(2)当E为中点时,求的度数.
21.先阅读材料,分解因式
解:令,则,所以,以上解题过程中用到了“整体思想”,整体思想是数学解题中常用的一种思想方法,请你运用这种思想方法解决下面的问题:
(1)分解因式
(2)分解因式
22.冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”深受广大人民的喜爱,某商场准备购进“冰墩墩”和“雪容融”这两款毛绒玩具共200个.已知:每个“冰墩墩”的进价比“雪容融”的进价多20元,用3000元购进“冰墩墩”的数量与用2400元购进“雪容融”的数量相同.
(1)请求出“冰墩墩”和“雪容融”这两款毛绒玩具的进价;
(2)若该商场分别以240元、160元的单价出售“冰墩墩”和“雪容融”这两款毛绒玩具,并将这两款毛绒玩具的总利润拟定在不少于21700元,且不超过22300元之间.问该商场共有几种进货方案?
23.探究题:观察下列各式的变化规律,然后解答下列问题:,,,,……
(1)计算:若为正整数,猜想______;
(2)化简;
(3)若,求的值.
24.图1中所示的遮阳伞,伞柄垂直于地面,其示意图如图.当伞收紧时,点与点重合;当伞慢慢撑开时,动点由向移动;当点到过点时,伞张得最开.已知伞在撑开的过程中,总有分米,分米,分米.
(1)求长的取值范围;
(2)当时,求的值.
25.为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽在组内做了如下尝试:如图1,在中,是边上的中线,延长到,使,连接.
(1)【探究发现】图1中中与的数量关系是 ,位置关系是 ;
(2)【初步应用】如图2,在中,若,,求边上的中线的取值范围;
(3)【探究提升】如图3,是的中线,过点分别向外作、,使得,,延长交于点,判断线段与的数量关系和位置关系,请说明理由.
参考答案:
1.C
【分析】本题考查全等三角形的判定.根据图形,利用即可得到一样的三角形.
【详解】解:由图可知,三角形有两个角及两个角的夹边是完好的,
∴根据即可画出一个一样的三角形.
故选C.
2.C
【分析】此题主要考查了多边形的对角线,根据边形从一个顶点出发可引出条对角线是解决问题的关键.
【详解】解:从八边形的一个顶点可以引:条对角线,
故选:C.
3.C
【分析】本题主要考查了三角形内角和定理,三角形三边关系,三角形的外角性质,解题的关键是灵活运用所学知识.
①根据三角形三边关系即可判断三条长度之比为的线段不能组成三角形;②由,结合三角形内角和定理,可求出,进而可判断是直角三角形;③根据三个内角度数之比,结合三角形内角和定理,可求出最大的内角为,从而得出该三角形是直角三角形;④利用外角的性质求出外角的度数,结合邻角互补,求出与该外角相邻的内角的度数为,从而得出该三角形是直角三角形.
【详解】解:①,3=3,
三条长度之比为的线段不能组成三角形,①不符合题意;
②,
,,
又,
,
该三角形是直角三角形,②符合题意;
③三角形的三个内角之比为,
最大内角的度数为,
该三角形是直角三角形,③符合题意;
④三角形的一个外角与它不相邻的两个内角和为,
该外角的度数为,
与该外角相邻的内角的度数为,
该三角形是直角三角形,④符合题意.
符合题意的有②③④.
故选:C.
4.D
【分析】本题考查了因式分解的定义,熟记“把一个多项式化成几个整式积的形式,像这样的式子变形叫做这个多项式的因式分解”是解题关键.
【详解】解:A、结果不是整式乘积的形式,不是因式分解,不符合题意,选项错误;
B、结果不是整式乘积的形式,不是因式分解,不符合题意,选项错误;
C、结果不是整式乘积的形式,不是因式分解,不符合题意,选项错误;
D、符合因式分解的定义,是因式分解,符合题意,选项正确;
故选:D.
5.A
【分析】本题考查解分式方程中的去分母化为整式方程的过程,关键是找到最简公分母,注意不要漏乘,单独的一个数和字母也必须乘最简公分,还有就是分子分母互为相反数时约分为.
【详解】解:
方程两边都乘得:.
故选:A.
6.C
【分析】本题考查了角平分线的性质定理,三角形的面积的计算,过作交的延长线于,根据角平分线的性质定理得到,根据三角形的面积公式即可得到结论,熟练掌握角平分线的性质定理,正确的作出辅助线是解题的关键.
【详解】如图,过作交的延长线于,
∵平分,,,
∴,
∴四边形的面积,
故选:.
7.C
【解析】略
8.B
【分析】本题考查等边三角形的性质和判定,轴对称最短问题等知识,解题的关键是学会利用轴对称解决最短问题,属于中考常考题型.作点P关于的对称点,连接交于,此时的值最小.最小值.
【详解】解:是等边三角形,
,,
,,,
,,
如图,作点P关于的对称点,连接交于,
此时的值最小.最小值,
,
∴,
∴,而,
是等边三角形,
,
的最小值为3.
故选B.
9.0
【解析】略
10. ; .
【分析】()将代入根据分式分母不为即可得到答案;
()将代入根据分式方程,解方程即可;
此题考查了分式有意义的条件和解分式方程,解题的关键是熟练掌握知识点的应用.
【详解】()当时,分式为,
要使分式有意义,则,解得:,
故答案为:;
()当时,分式方程为,
则,
∴,
经检验,是原分式方程的解,
故答案为:.
11./度
【分析】本题主要考查的是三角形内角和定理,由图可知,直角三角形的两个锐角正好是和的对顶角,而直角三角形的两个锐角之和是,那么就可得知的度数.
【详解】解:由图可知,
和的对顶角互余,
,
故答案为:.
12./度
【分析】本题主要考查的全等三角形中对应角的关系,理解全等三角形中对应角相等,找出角与角的和差关系.根据可求出,从而,即可得到.
【详解】解:,
,
,
,
故答案为:.
13.(答案不唯一)
【分析】本题考查添加合适的条件证明三角形全等,根据判断两个直角三角形全等,即可.掌握全等三角形的判定方法,是解题的关键.
【详解】解:∵,
∴当添加条件为时,根据,即可得到;
故答案为:(答案不唯一).
14. 10 5
【分析】本题主要考查了角平分线的性质,平行线的性质的应用,求出,即可得出,根据角平分线的性质得出是解题的关键.
【详解】∵平分,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
过P作于点E,
∵,平分,
∴,
∵,,
∴,
在中,
,
∴,
故答案为:,.
15.
【解析】略
16.或
【分析】本题主要考查整式的混合运算,分别表示出底面的长和宽,再根据面积公式进行计算即可.
【详解】解:因为长方形纸板的长为,宽为,小正方形的边长为1,
所以,该无盖纸盒的底面的长为,宽为,
所以,该无盖纸盒的底面积为或
故答案为:或.
17.,
【分析】本题考查了整式的化简,首先根据单项式与多项式相乘的法则去掉括号,然后合并同类项,最后代入已知的数值计算即可.
【详解】解:
,
当时,原式.
18.
【分析】本题考查了三角形内角和定理、角平分线的定义、垂线的定义,由三角形内角和定理可得,由角平分线的定义可得,再由三角形内角和定理可得,由垂线的定义可得,最后由进行计算即可,熟练掌握三角形内角和定理、角平分线的定义、垂线的定义是解此题的关键.
【详解】解:在中,,
,
平分,
,
,
,
,
.
19.见解析
【分析】本题考查了全等三角形的判定和性质;熟练掌握两边和它们的夹角对应相等的两个三角形全等;全等三角形的对应边对应角相等是解题的关键.
根据题意可得,;推得,根据全等三角形的判定和性质即可证明.
【详解】证明:∵,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,
∴.
20.(1),理由见解析
(2)
【分析】本题考查等边三角形的性质,全等三角形的判定和性质:
(1)根据等边三角形的性质,依据证明,可得;
(2)根据三线合一可得当E为中点时,,根据全等三角形对应角相等可得.
【详解】(1)解:,理由如下:
和是等边三角形,
,,,
在和中,
,
,
;
(2)解:是等边三角形,
当E为中点时,,
,
由(1)知,
.
21.(1)
(2)
【分析】本题考查了整体思想的应用于因式分解,熟练掌握思想的内涵是解题的关键.
(1)令,原式变形为,还原即可.
(2) 令,.还原即可.
【详解】(1)令,原式变形为,
.
(2)令,.
故.
22.(1)每个“雪容融”的进价为80元,则每个“冰墩墩”的进价为100元;
(2)11
【分析】此题考查了分式方程的实际应用,一元一次不等式组的实际应用,正确理解题意列得方程及不等式是解题的关键.
(1)设每个“雪容融”的进价为x元,则每个“冰墩墩”的进价为元,根据用3000元购进“冰墩墩”的数量与用2400元购进“雪容融”的数量相同列分式方程求解;
(2)设购买“冰墩墩”a个,则购买“雪容融”个,列不等式组求解.
【详解】(1)设每个“雪容融”的进价为x元,则每个“冰墩墩”的进价为元,可得
解得,
经检验是方程的根,且符合题意,
∴,
答:每个“雪容融”的进价为80元,则每个“冰墩墩”的进价为100元;
(2)设购买“冰墩墩”a个,则购买“雪容融”个,则
解得,且a为正整数,
∴该商场进货方案有11种.
23.(1)
(2)
(3)
【分析】本题考查了非负数的性质、有理数的混合运算、分式的加法,弄清题中的拆项法则是解本题的关键.
(1)根据已知等式得到一般性规律,写出即可;
(2)利用(1)中得到的规律,变形后,进行计算即可;
(3)利用非负数的性质求出与的值,代入原式计算即可得出答案.
【详解】(1)解:,,,,…,
若为正整数,,
故答案为:;
(2)解:由(1)可得,
;
(3)解:,,,
,,
,,
.
24.(1);
(2)分米
【分析】题目主要考查线段间的数量关系,等边三角形的判定和性质;
(1)根据题意,得,进一步求得的长,即可求得的取值范围;
(2)由等边三角形的判定和性质得出为等边三角形,分米,再结合图形求解即可.
【详解】(1)解:分米,分米,
分米.
的取值范围是:;
(2)根据题意得,=,
为等边三角形,
分米,
分米,
分米.
25.(1),
(2)
(3),,理由见解析
【分析】(1)证,得,,再由平行线的判定即可得出;
(2)延长到,使,连接,由(1)可知,,得,再由三角形的三边关系即可得出结论;
(3)延长到,使得,连接,由(1)可知,,得,再证,得,,则,然后由三角形的外角性质证出,即可得出结论.
【详解】(1)解:是的中线,
,
在和中,
,
,
,,
,
故答案为:,;
(2)如图2,延长到,使,连接,
由(1)可知,,
,
在中,,
,
即,
,
即边上的中线的取值范围为;
(3),,理由如下:
如图3,延长到,使得,连接,
由(1)可知,,
,
,
,
由(2)可知,,
,
、,
,
,
,
在和中,
,
,
,,
,
,
,
,
,
.
【点睛】本题是三角形综合题,考查了全等三角形的判定与性质、倍长中线法、三角形的三边关系、平行线的判定与性质以及三角形的外角性质,添加辅助线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末易错精选题练习-2023-2024学年数学八年级上册人教版
一、单选题
1.如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
A. B. C. D.
2.过八边形的一个顶点最多可以引对角线的条数为( )
A.3 B.4 C.5 D.6
3.下列三角形一定为直角三角形的是( )
①三角形的三边之比为;②的三个内角的关系为;③三角形的三个内角之比为;④三角形的一个外角与它不相邻的两个内角和为.
A.1个 B.2个 C.3个 D.4个
4.下列各式从左到右的变形中,是因式分解的为( )
A. B.
C. D.
5.分式方程约去分母得( )
A. B.
C. D.
6.如图,在四边形中,,平分,,,,则四边形的面积是( )
A. B. C. D.
7.若,则,分别为( )
A., B., C., D.,
8.如图,在等边三角形中,是中线,点P,Q分别在,上,且,动点E在上,则的最小值为( )
A.2 B.3 C.4 D.5
二、填空题
9.若与互为相反数,则 .
10.已知分式.
(1)如果,那么的取值范围是 .
(2)若,且,则的值为 .
11.如图,某同学在课桌上无意中将一块三角尺叠放在直尺上,则 .
12.如图,己知,则 .
13.如图,在和中,,请你添加一个适当的条件,使,添加的条件是: .(写出一个即可)
14.如图,,平分,于D,交于C.若则 , .
15.如图,六边形是轴对称图形,所在的直线是它的对称轴.若,则的大小是 .
16.如图,杨老师在《制作长方体纸盒的活动》这一课中,把一张长方形纸板的四周各剪去一个同样大小的小正方形,然后将四周突出部分折起,制成一个长方体形状的无盖纸盒 如图所示,长方形纸板的长为,宽为,小正方形的边长为1.该无盖纸盒的底面积为 用含,的式子表示
三、解答题
17.先化简,再求值:,其中.
18.如图,在中,,平分,交于点,求的度数.
19.如图,在中,,,过点作,垂足为点,在直线上截取.求证:.
20.如图,在等边三角形中,点E是边上一动点(不与B,C重合),以为边在的下方作等边三角形,连接,.
(1)在运动的过程中,与有何数量关系?请说明理由.
(2)当E为中点时,求的度数.
21.先阅读材料,分解因式
解:令,则,所以,以上解题过程中用到了“整体思想”,整体思想是数学解题中常用的一种思想方法,请你运用这种思想方法解决下面的问题:
(1)分解因式
(2)分解因式
22.冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”深受广大人民的喜爱,某商场准备购进“冰墩墩”和“雪容融”这两款毛绒玩具共200个.已知:每个“冰墩墩”的进价比“雪容融”的进价多20元,用3000元购进“冰墩墩”的数量与用2400元购进“雪容融”的数量相同.
(1)请求出“冰墩墩”和“雪容融”这两款毛绒玩具的进价;
(2)若该商场分别以240元、160元的单价出售“冰墩墩”和“雪容融”这两款毛绒玩具,并将这两款毛绒玩具的总利润拟定在不少于21700元,且不超过22300元之间.问该商场共有几种进货方案?
23.探究题:观察下列各式的变化规律,然后解答下列问题:,,,,……
(1)计算:若为正整数,猜想______;
(2)化简;
(3)若,求的值.
24.图1中所示的遮阳伞,伞柄垂直于地面,其示意图如图.当伞收紧时,点与点重合;当伞慢慢撑开时,动点由向移动;当点到过点时,伞张得最开.已知伞在撑开的过程中,总有分米,分米,分米.
(1)求长的取值范围;
(2)当时,求的值.
25.为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽在组内做了如下尝试:如图1,在中,是边上的中线,延长到,使,连接.
(1)【探究发现】图1中中与的数量关系是 ,位置关系是 ;
(2)【初步应用】如图2,在中,若,,求边上的中线的取值范围;
(3)【探究提升】如图3,是的中线,过点分别向外作、,使得,,延长交于点,判断线段与的数量关系和位置关系,请说明理由.
参考答案:
1.C
【分析】本题考查全等三角形的判定.根据图形,利用即可得到一样的三角形.
【详解】解:由图可知,三角形有两个角及两个角的夹边是完好的,
∴根据即可画出一个一样的三角形.
故选C.
2.C
【分析】此题主要考查了多边形的对角线,根据边形从一个顶点出发可引出条对角线是解决问题的关键.
【详解】解:从八边形的一个顶点可以引:条对角线,
故选:C.
3.C
【分析】本题主要考查了三角形内角和定理,三角形三边关系,三角形的外角性质,解题的关键是灵活运用所学知识.
①根据三角形三边关系即可判断三条长度之比为的线段不能组成三角形;②由,结合三角形内角和定理,可求出,进而可判断是直角三角形;③根据三个内角度数之比,结合三角形内角和定理,可求出最大的内角为,从而得出该三角形是直角三角形;④利用外角的性质求出外角的度数,结合邻角互补,求出与该外角相邻的内角的度数为,从而得出该三角形是直角三角形.
【详解】解:①,3=3,
三条长度之比为的线段不能组成三角形,①不符合题意;
②,
,,
又,
,
该三角形是直角三角形,②符合题意;
③三角形的三个内角之比为,
最大内角的度数为,
该三角形是直角三角形,③符合题意;
④三角形的一个外角与它不相邻的两个内角和为,
该外角的度数为,
与该外角相邻的内角的度数为,
该三角形是直角三角形,④符合题意.
符合题意的有②③④.
故选:C.
4.D
【分析】本题考查了因式分解的定义,熟记“把一个多项式化成几个整式积的形式,像这样的式子变形叫做这个多项式的因式分解”是解题关键.
【详解】解:A、结果不是整式乘积的形式,不是因式分解,不符合题意,选项错误;
B、结果不是整式乘积的形式,不是因式分解,不符合题意,选项错误;
C、结果不是整式乘积的形式,不是因式分解,不符合题意,选项错误;
D、符合因式分解的定义,是因式分解,符合题意,选项正确;
故选:D.
5.A
【分析】本题考查解分式方程中的去分母化为整式方程的过程,关键是找到最简公分母,注意不要漏乘,单独的一个数和字母也必须乘最简公分,还有就是分子分母互为相反数时约分为.
【详解】解:
方程两边都乘得:.
故选:A.
6.C
【分析】本题考查了角平分线的性质定理,三角形的面积的计算,过作交的延长线于,根据角平分线的性质定理得到,根据三角形的面积公式即可得到结论,熟练掌握角平分线的性质定理,正确的作出辅助线是解题的关键.
【详解】如图,过作交的延长线于,
∵平分,,,
∴,
∴四边形的面积,
故选:.
7.C
【解析】略
8.B
【分析】本题考查等边三角形的性质和判定,轴对称最短问题等知识,解题的关键是学会利用轴对称解决最短问题,属于中考常考题型.作点P关于的对称点,连接交于,此时的值最小.最小值.
【详解】解:是等边三角形,
,,
,,,
,,
如图,作点P关于的对称点,连接交于,
此时的值最小.最小值,
,
∴,
∴,而,
是等边三角形,
,
的最小值为3.
故选B.
9.0
【解析】略
10. ; .
【分析】()将代入根据分式分母不为即可得到答案;
()将代入根据分式方程,解方程即可;
此题考查了分式有意义的条件和解分式方程,解题的关键是熟练掌握知识点的应用.
【详解】()当时,分式为,
要使分式有意义,则,解得:,
故答案为:;
()当时,分式方程为,
则,
∴,
经检验,是原分式方程的解,
故答案为:.
11./度
【分析】本题主要考查的是三角形内角和定理,由图可知,直角三角形的两个锐角正好是和的对顶角,而直角三角形的两个锐角之和是,那么就可得知的度数.
【详解】解:由图可知,
和的对顶角互余,
,
故答案为:.
12./度
【分析】本题主要考查的全等三角形中对应角的关系,理解全等三角形中对应角相等,找出角与角的和差关系.根据可求出,从而,即可得到.
【详解】解:,
,
,
,
故答案为:.
13.(答案不唯一)
【分析】本题考查添加合适的条件证明三角形全等,根据判断两个直角三角形全等,即可.掌握全等三角形的判定方法,是解题的关键.
【详解】解:∵,
∴当添加条件为时,根据,即可得到;
故答案为:(答案不唯一).
14. 10 5
【分析】本题主要考查了角平分线的性质,平行线的性质的应用,求出,即可得出,根据角平分线的性质得出是解题的关键.
【详解】∵平分,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
过P作于点E,
∵,平分,
∴,
∵,,
∴,
在中,
,
∴,
故答案为:,.
15.
【解析】略
16.或
【分析】本题主要考查整式的混合运算,分别表示出底面的长和宽,再根据面积公式进行计算即可.
【详解】解:因为长方形纸板的长为,宽为,小正方形的边长为1,
所以,该无盖纸盒的底面的长为,宽为,
所以,该无盖纸盒的底面积为或
故答案为:或.
17.,
【分析】本题考查了整式的化简,首先根据单项式与多项式相乘的法则去掉括号,然后合并同类项,最后代入已知的数值计算即可.
【详解】解:
,
当时,原式.
18.
【分析】本题考查了三角形内角和定理、角平分线的定义、垂线的定义,由三角形内角和定理可得,由角平分线的定义可得,再由三角形内角和定理可得,由垂线的定义可得,最后由进行计算即可,熟练掌握三角形内角和定理、角平分线的定义、垂线的定义是解此题的关键.
【详解】解:在中,,
,
平分,
,
,
,
,
.
19.见解析
【分析】本题考查了全等三角形的判定和性质;熟练掌握两边和它们的夹角对应相等的两个三角形全等;全等三角形的对应边对应角相等是解题的关键.
根据题意可得,;推得,根据全等三角形的判定和性质即可证明.
【详解】证明:∵,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,
∴.
20.(1),理由见解析
(2)
【分析】本题考查等边三角形的性质,全等三角形的判定和性质:
(1)根据等边三角形的性质,依据证明,可得;
(2)根据三线合一可得当E为中点时,,根据全等三角形对应角相等可得.
【详解】(1)解:,理由如下:
和是等边三角形,
,,,
在和中,
,
,
;
(2)解:是等边三角形,
当E为中点时,,
,
由(1)知,
.
21.(1)
(2)
【分析】本题考查了整体思想的应用于因式分解,熟练掌握思想的内涵是解题的关键.
(1)令,原式变形为,还原即可.
(2) 令,.还原即可.
【详解】(1)令,原式变形为,
.
(2)令,.
故.
22.(1)每个“雪容融”的进价为80元,则每个“冰墩墩”的进价为100元;
(2)11
【分析】此题考查了分式方程的实际应用,一元一次不等式组的实际应用,正确理解题意列得方程及不等式是解题的关键.
(1)设每个“雪容融”的进价为x元,则每个“冰墩墩”的进价为元,根据用3000元购进“冰墩墩”的数量与用2400元购进“雪容融”的数量相同列分式方程求解;
(2)设购买“冰墩墩”a个,则购买“雪容融”个,列不等式组求解.
【详解】(1)设每个“雪容融”的进价为x元,则每个“冰墩墩”的进价为元,可得
解得,
经检验是方程的根,且符合题意,
∴,
答:每个“雪容融”的进价为80元,则每个“冰墩墩”的进价为100元;
(2)设购买“冰墩墩”a个,则购买“雪容融”个,则
解得,且a为正整数,
∴该商场进货方案有11种.
23.(1)
(2)
(3)
【分析】本题考查了非负数的性质、有理数的混合运算、分式的加法,弄清题中的拆项法则是解本题的关键.
(1)根据已知等式得到一般性规律,写出即可;
(2)利用(1)中得到的规律,变形后,进行计算即可;
(3)利用非负数的性质求出与的值,代入原式计算即可得出答案.
【详解】(1)解:,,,,…,
若为正整数,,
故答案为:;
(2)解:由(1)可得,
;
(3)解:,,,
,,
,,
.
24.(1);
(2)分米
【分析】题目主要考查线段间的数量关系,等边三角形的判定和性质;
(1)根据题意,得,进一步求得的长,即可求得的取值范围;
(2)由等边三角形的判定和性质得出为等边三角形,分米,再结合图形求解即可.
【详解】(1)解:分米,分米,
分米.
的取值范围是:;
(2)根据题意得,=,
为等边三角形,
分米,
分米,
分米.
25.(1),
(2)
(3),,理由见解析
【分析】(1)证,得,,再由平行线的判定即可得出;
(2)延长到,使,连接,由(1)可知,,得,再由三角形的三边关系即可得出结论;
(3)延长到,使得,连接,由(1)可知,,得,再证,得,,则,然后由三角形的外角性质证出,即可得出结论.
【详解】(1)解:是的中线,
,
在和中,
,
,
,,
,
故答案为:,;
(2)如图2,延长到,使,连接,
由(1)可知,,
,
在中,,
,
即,
,
即边上的中线的取值范围为;
(3),,理由如下:
如图3,延长到,使得,连接,
由(1)可知,,
,
,
,
由(2)可知,,
,
、,
,
,
,
在和中,
,
,
,,
,
,
,
,
,
.
【点睛】本题是三角形综合题,考查了全等三角形的判定与性质、倍长中线法、三角形的三边关系、平行线的判定与性质以及三角形的外角性质,添加辅助线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
